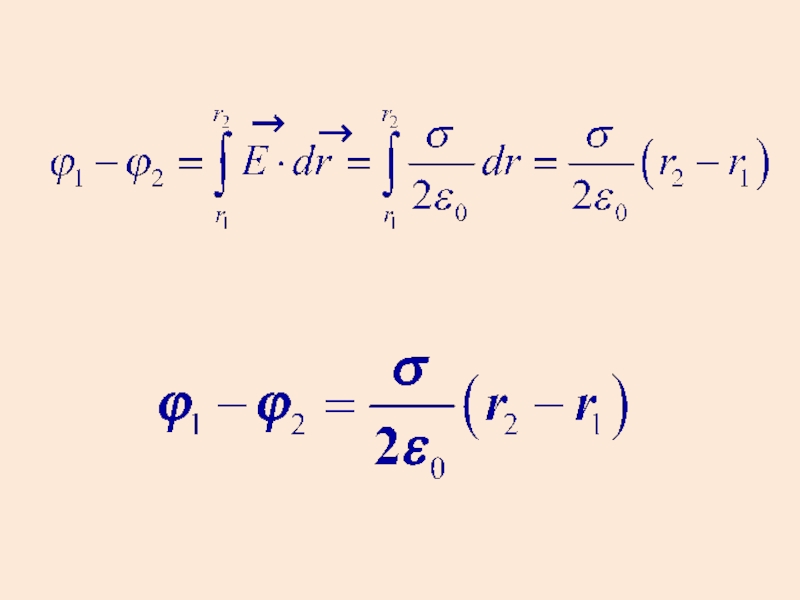пронизывающих поверхность S .
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поток вектора E презентация
Содержание
- 1. Поток вектора E
- 2. Если линии перпендикулярны поверхности, а поле однородно, то просто
- 3. Если поле неоднородно, то поверхность S надо
- 4. Такие очень малые плоские площадки dS называют
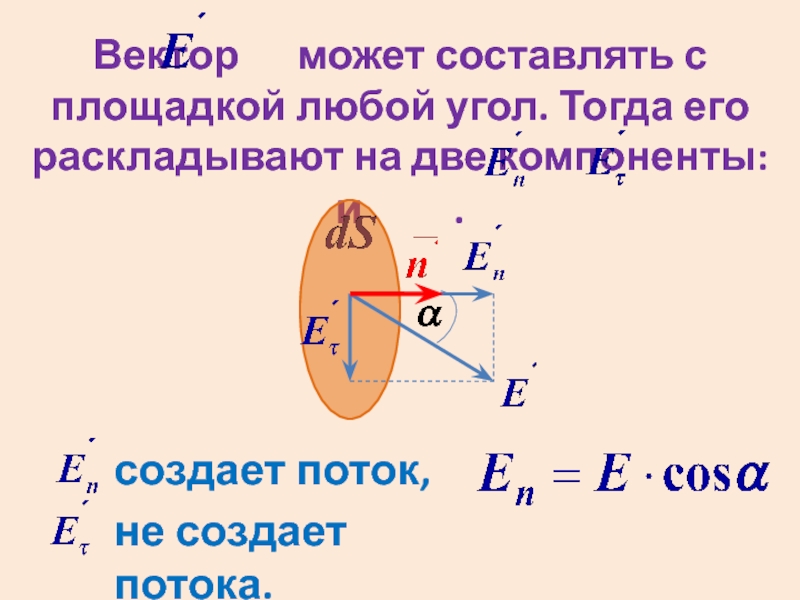
- 5. Вектор может составлять с площадкой
- 6. Элементарный поток угол между вектором и нормалью к площадке
- 7. проекция вектора на направление нормали к площадке. Именно ее значение определяет величину потока.
- 8. Введем такой вектор ,
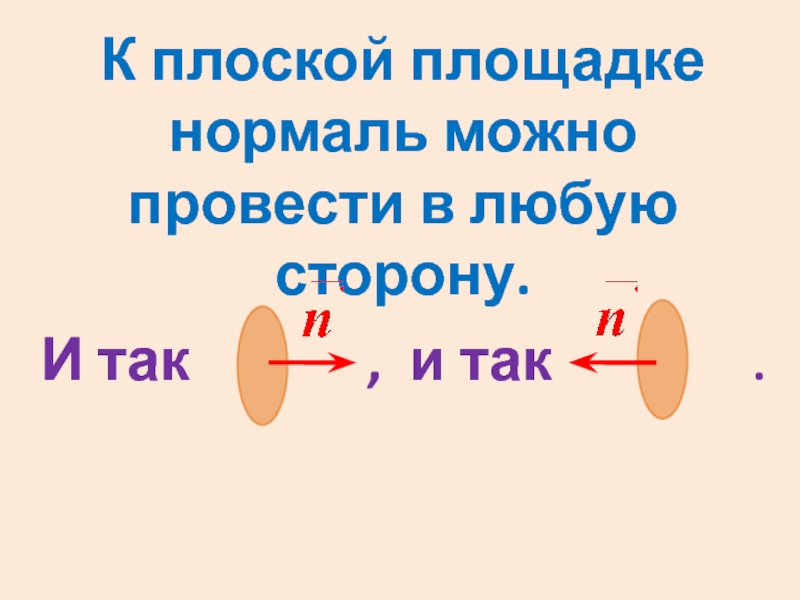
- 9. К плоской площадке нормаль можно провести в
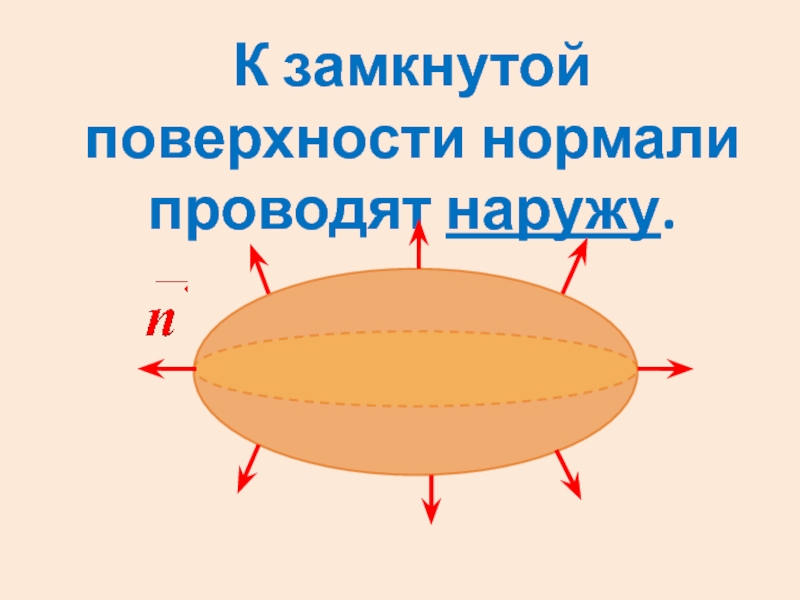
- 10. К замкнутой поверхности нормали проводят наружу.
- 11. Поток м. б. и + , и
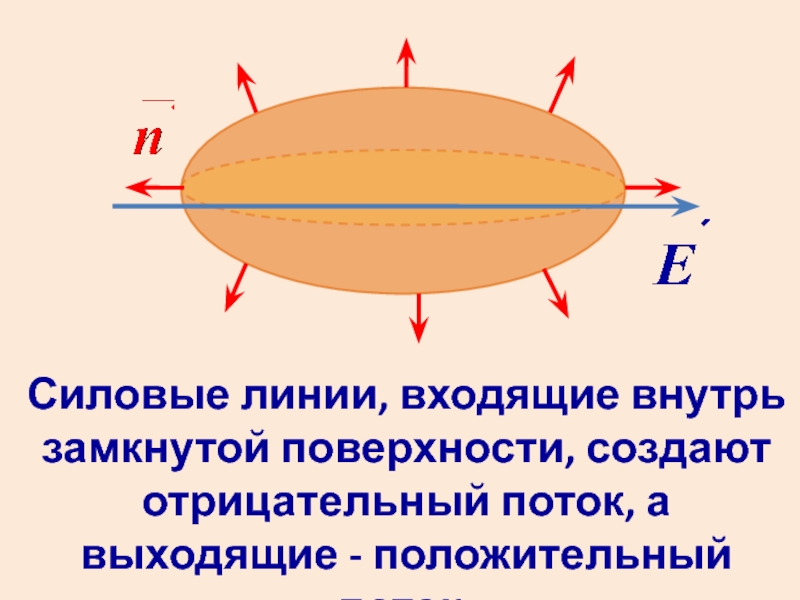
- 12. Силовые линии, входящие внутрь замкнутой
- 13. Чтобы найти поток через всю поверхность S, надо интегрировать:
- 14. Часто это сложная задача, так как и
- 15. Теорема Гаусса Поток вектора сквозь
- 17. Что дает эта теорема? 1. Утверждает, что электростатическое поле имеет источники, которыми являются заряды.
- 18. Когда заряд попадает внутрь поверхности S –
- 19. Положительный заряд создает положительный поток (источник поля),
- 20. Не любое поле имеет источники.
- 21. 2. В некоторых случаях теорема Гаусса позволяет
- 22. Расчет полей по теореме Гаусса Кроме найдем разность потенциалов двух точек поля.
- 23. 1. Поле точечного заряда. Видно, что поток
- 24. Проще всего найти поток через сферу, т.к.
- 25. - площадь сферы А по теореме Гаусса
- 26. Приравниваем правые части:
- 27. Пришли к известной формуле напряженности. Теорема Гаусса – полевая формулировка закона Кулона.
- 28. Найдем разность потенциалов двух точек поля точечного заряда:
- 29. Потенциал поля точечного заряда
- 30. 2. Поле равномерно заряженной сферы
- 31. При
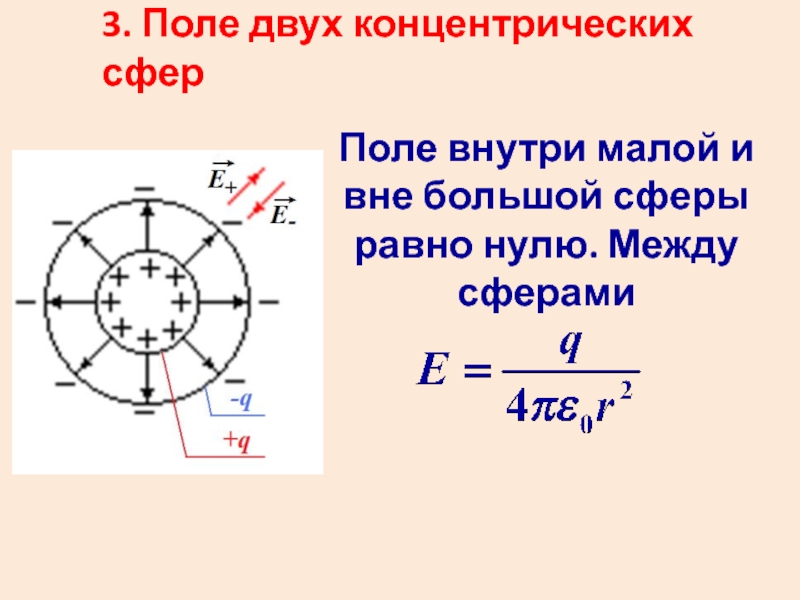
- 32. 3. Поле двух концентрических сфер Поле
- 33. 4. Поле равномерно заряженного шара
- 34. При
- 35. Объемная плотность заряда шара: Объем внутри малой сферы: Заряд внутри малой сферы:
- 36. Применяем теорему Гаусса
- 37. В центре шара Е=0. Затем Е линейно
- 38. 5. Поле бесконечной нити (цилиндра)
- 39. Поток через боковую поверхность Sбок: Поток через “донышки” цилиндра равен нулю.
- 40. По теореме Гаусса
- 41. Найдем разность потенциалов между точками поля, находящимися на расстояниях r1 и r2 от нити:
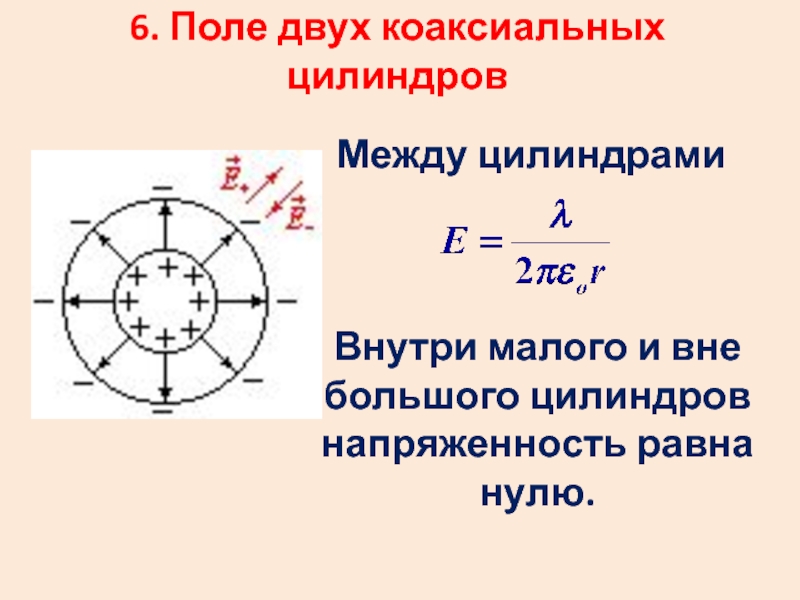
- 42. 6. Поле двух коаксиальных цилиндров Между цилиндрами
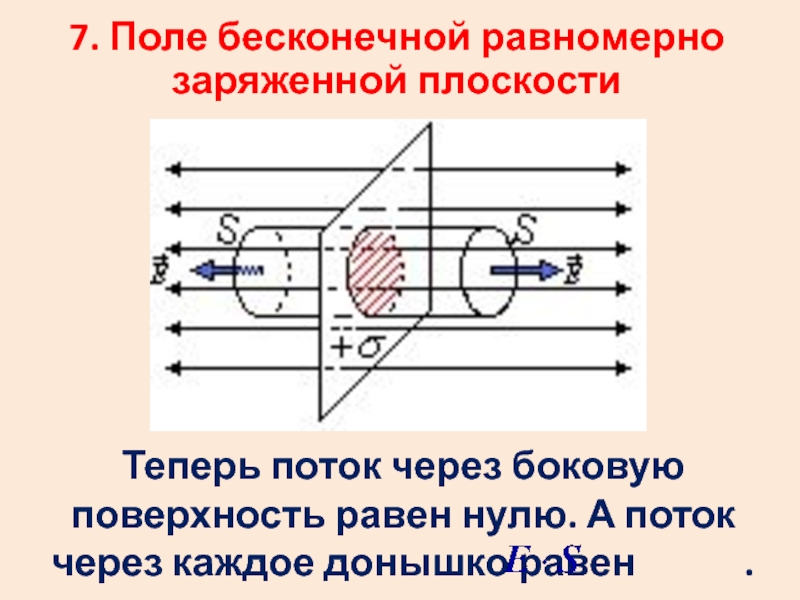
- 43. 7. Поле бесконечной равномерно заряженной плоскости Теперь
- 44. По теореме Гаусса
- 45. Поле бесконечной плоскости не зависит от координат (однородно).
- 47. 8. Поле двух плоскостей
- 48. Снаружи плоскостей поле равно нулю. Между плоскостями поле усиливается в два раза.
Если линии перпендикулярны поверхности, а поле однородно, то просто
Слайд 3Если поле неоднородно, то поверхность S надо разбить на участки dS
настолько малые, чтобы в пределах этих участков поле можно было считать однородным.
Слайд 4Такие очень малые плоские площадки dS называют элементарными, а поток сквозь
них – элементарным потоком dФ.
Слайд 5Вектор может составлять с площадкой любой угол. Тогда его
раскладывают на две компоненты: и .
создает поток,
не создает потока.
Слайд 7проекция вектора на направление нормали к площадке.
Именно ее значение
определяет величину потока.
Слайд 8Введем такой вектор , чтобы его модуль был
равен величине площади, а направление совпадало с вектором нормали .
α
Слайд 12
Силовые линии, входящие внутрь замкнутой поверхности, создают отрицательный поток, а выходящие
- положительный поток.
Слайд 14Часто это сложная задача, так как и угол, и величина напряжен-ности
в разных точках поверхности могут быть разными.
Слайд 15Теорема Гаусса
Поток вектора сквозь замкнутую поверхность равен суммарному заряду
внутри объёма, ограниченного
этой поверхностью, делённому на .
этой поверхностью, делённому на .
Слайд 17Что дает эта теорема?
1. Утверждает, что электростатическое поле имеет источники, которыми
являются заряды.
Слайд 18Когда заряд попадает внутрь поверхности S – есть поток,
А когда не
попадает – нет потока (сколько линий вошло, столько и вышло).
Слайд 19Положительный заряд создает положительный поток (источник поля), а отрицательный заряд
– отрицательный поток (сток поля).
Слайд 212. В некоторых случаях теорема Гаусса позволяет очень просто рассчитать напряженность
поля.
Этих случаев мало. Поток должен легко находиться. Для этого нужна высокая степень симметрии поля.
Слайд 231. Поле точечного заряда.
Видно, что поток через любую поверхность одинаков (число
линий одно и то же).
Слайд 24Проще всего найти поток через сферу, т.к.
в каждой точке сферы
Е одинакова;
угол между и равен нулю.
угол между и равен нулю.
Слайд 27Пришли к известной формуле напряженности.
Теорема Гаусса – полевая формулировка закона Кулона.
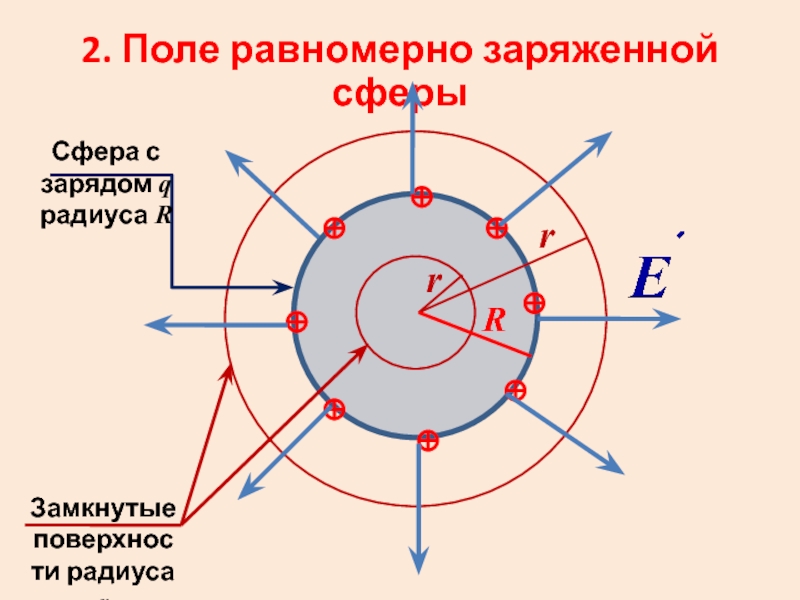
Слайд 302. Поле равномерно заряженной сферы
Сфера с зарядом q радиуса R
Замкнутые поверхности
радиуса r
R
r
r
Слайд 31При замкнутая поверхность
не содержит
зарядов, поэтому внутри
сферы
2) При так же, как и для точечного заряда по теореме Гаусса
сферы
2) При так же, как и для точечного заряда по теореме Гаусса
Слайд 323. Поле двух концентрических сфер
Поле внутри малой и вне большой
сферы равно нулю. Между сферами
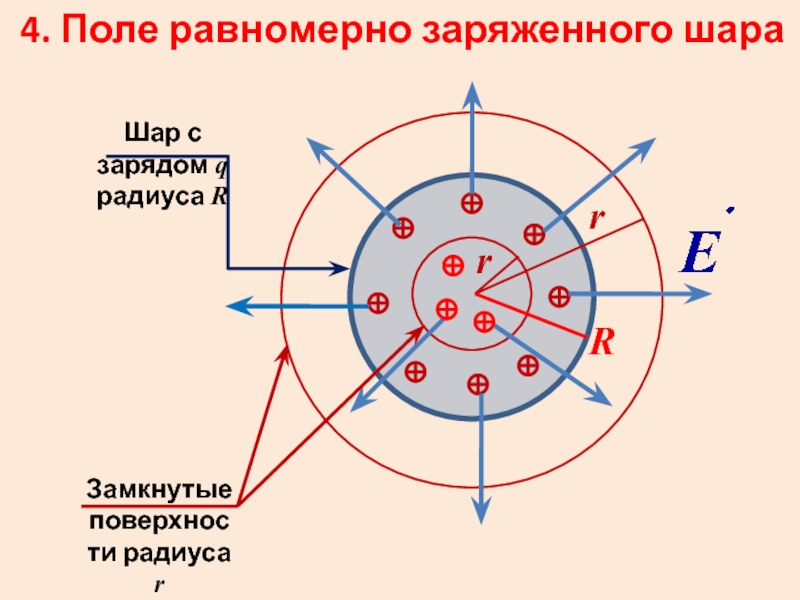
Слайд 334. Поле равномерно заряженного шара
Шар с зарядом q радиуса R
Замкнутые
поверхности радиуса r
R
r
r
Слайд 34
При поле такое же, как у
сферы и точечного заряда
При нужно рассчитать, какой заряд попадает внутрь малой замкнутой сферической поверхности.
При нужно рассчитать, какой заряд попадает внутрь малой замкнутой сферической поверхности.
Слайд 37В центре шара Е=0. Затем Е линейно растет по мере удаления
от центра к границе шара. Вне шара напряженность поля шара та же, что и у точечного заряда.
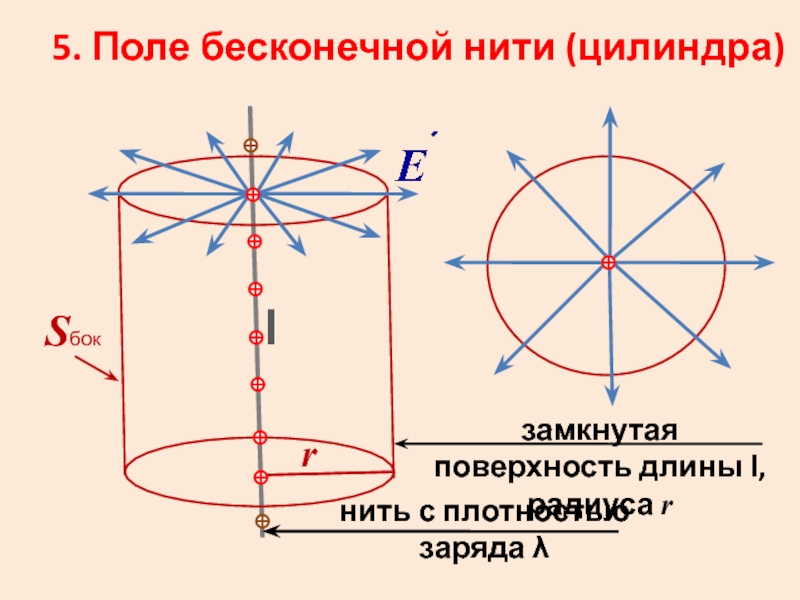
Слайд 385. Поле бесконечной нити (цилиндра)
нить с плотностью заряда λ
замкнутая поверхность
длины l, радиуса r
r
Sбок
l
Слайд 41Найдем разность потенциалов между точками поля, находящимися на расстояниях r1 и
r2 от нити:
Слайд 426. Поле двух коаксиальных цилиндров
Между цилиндрами
Внутри малого и вне большого
цилиндров напряженность равна нулю.
Слайд 437. Поле бесконечной равномерно заряженной плоскости
Теперь поток через боковую поверхность равен
нулю. А поток через каждое донышко равен .
