- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение изображений в линзах презентация
Содержание
- 1. Построение изображений в линзах
- 2. Линзы Линза — это оптически прозрачное однородное
- 3. Линзы Линзы бывают двояковыпуклые двояковогнутые плосковыпуклые плосковогнутые вогнуто-выпуклые выпукло-вогнутые СОБИРАЮЩИЕ РАССЕИВАЮЩИЕ
- 4. Линзы
- 5. Линзы Теорема об изображении Если перед линзой
- 6. Линзы ИЗОБРАЖЕНИЕ действительное мнимое изображение,
- 7. Линзы действительное изображение
- 8. Линзы мнимое изображение
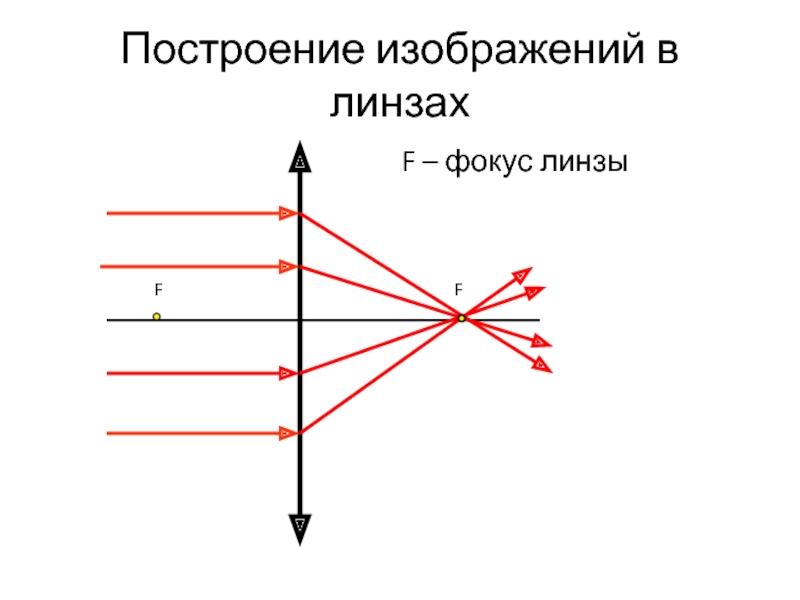
- 9. Построение изображений в линзах Фокус – точка,
- 10. Построение изображений в линзах F F F – фокус линзы
- 11. Построение изображений в линзах При построении изображения
- 12. Построение изображений в линзах Главная
- 13. Ход лучей в линзе
- 14. Ход лучей в линзе
- 15. Ход лучей в линзе
- 16. Ход лучей в линзе луч,
- 17. Ход лучей в линзе С помощью данных
- 18. Построение изображений в линзе Изображение точечного источника
- 19. Построение изображений в линзе Изображение точечного источника
- 20. Построение изображений в линзе Изображение точечного источника света a > f:
- 21. Построение изображений в линзе Изображение точечного источника
- 22. Построение изображений в линзе Изображение точечного источника
- 23. Построение изображений в линзе Изображение точечного источника
- 24. Построение изображений в линзе Изображение точечного источника
- 25. Построение изображений в линзе Изображение точечного источника
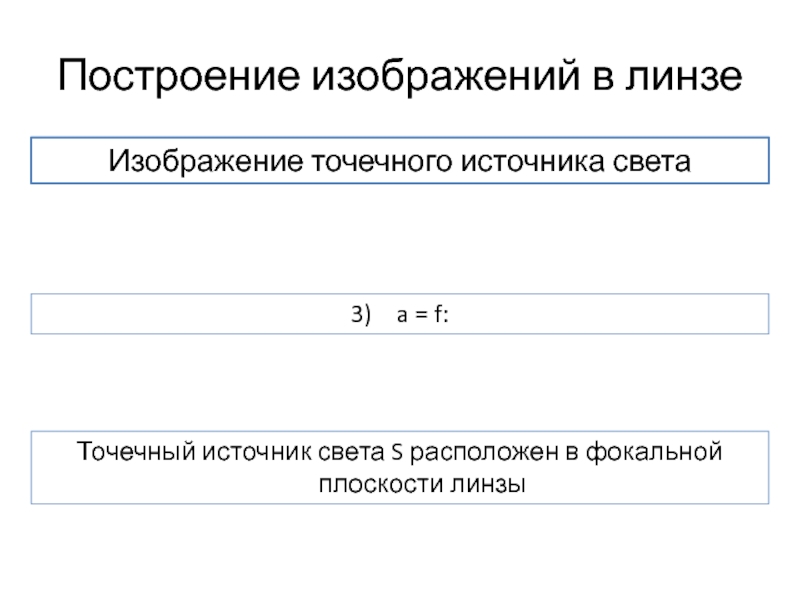
- 26. Построение изображений в линзе Изображение точечного источника света 3) a = f:
- 27. Построение изображений в линзе Изображение предмета 1)
- 28. Построение изображений в линзе Изображение предмета a)
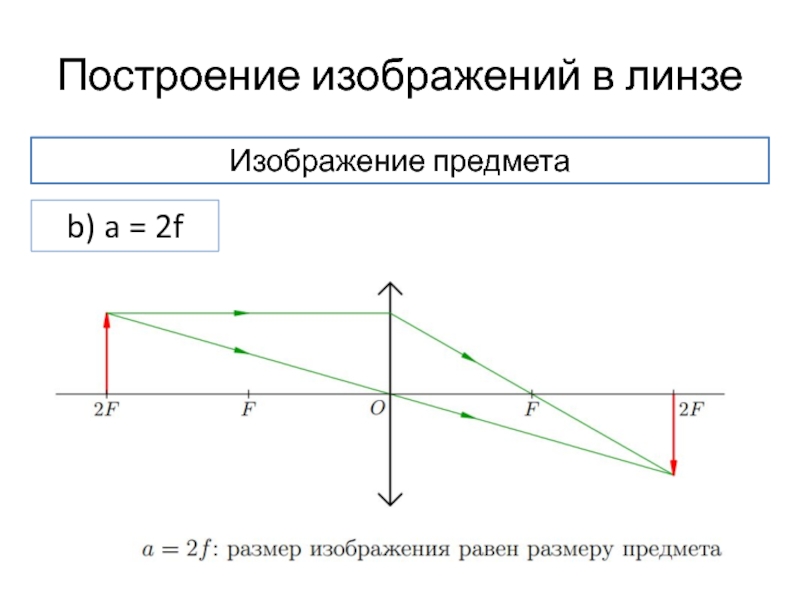
- 29. Построение изображений в линзе Изображение предмета b) a = 2f
- 30. Построение изображений в линзе Изображение предмета с)
- 31. Построение изображений в линзе Изображение предмета a < f
- 32. Лабораторная работа №9 ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ В ЛИНЗЕ
- 33. Используя лучи и примеры построений,
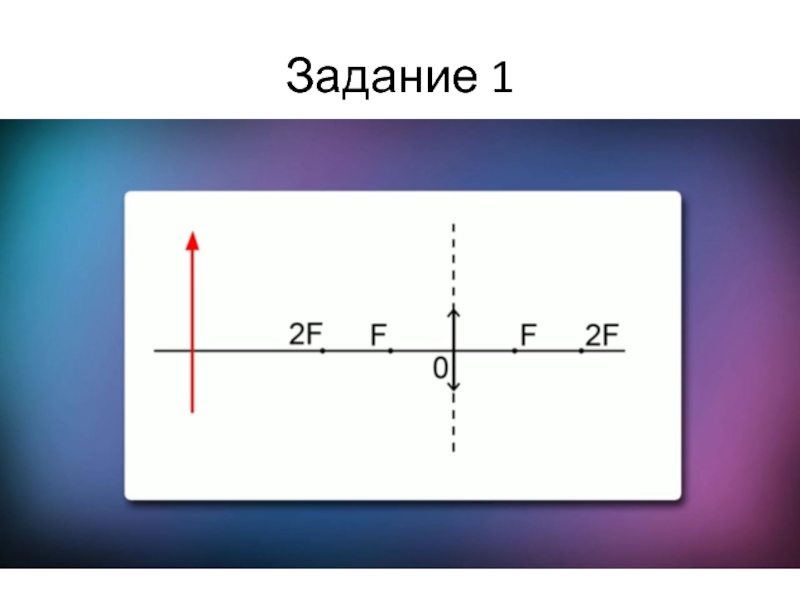
- 34. Задание 1
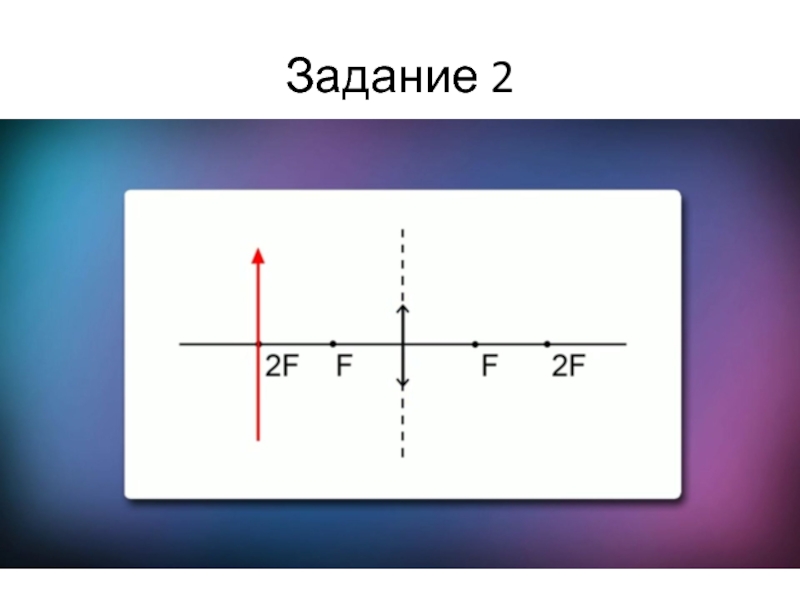
- 35. Задание 2
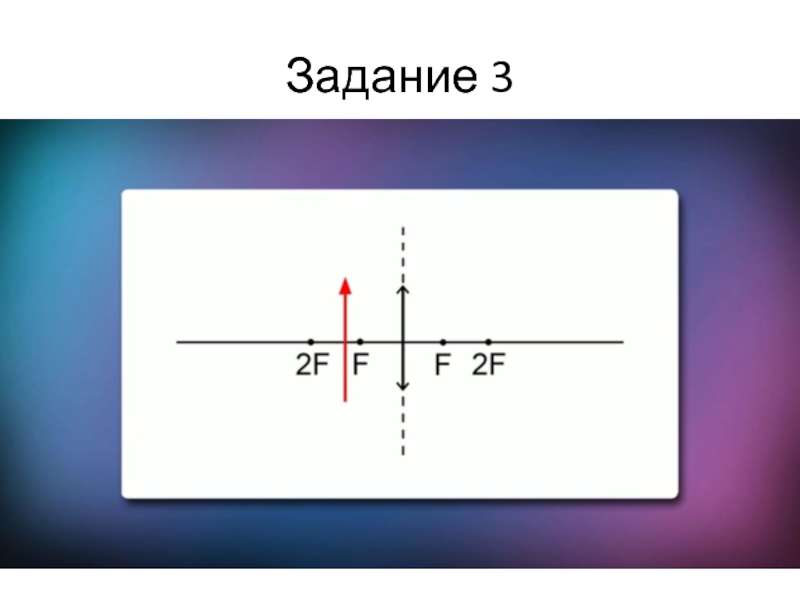
- 36. Задание 3
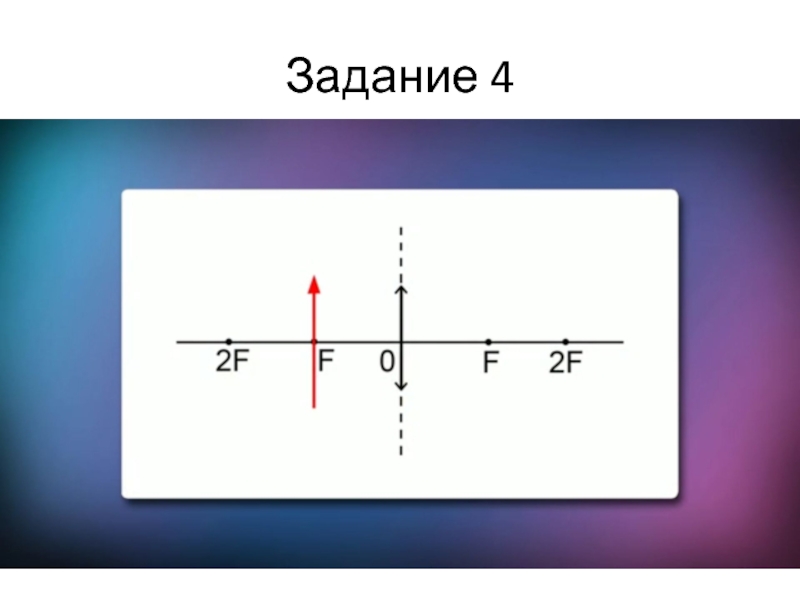
- 37. Задание 4
Слайд 2Линзы
Линза — это оптически прозрачное однородное тело, ограниченное с двух сторон
Является существенной деталью таких оптических приборов как фотоаппараты, бинокли, микроскопы и др.
Линзы обычно изготавливаются из стекла или специальных прозрачных пластмасс.
Слайд 3Линзы
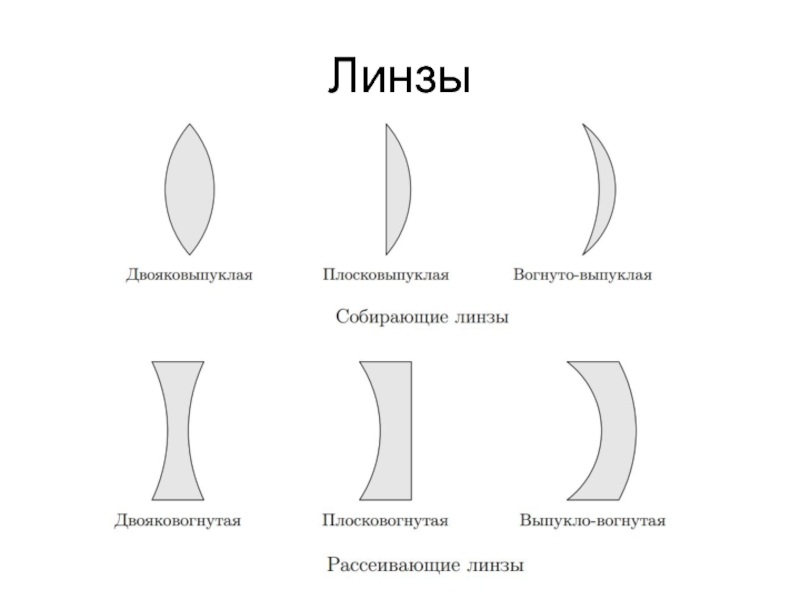
Линзы бывают
двояковыпуклые
двояковогнутые
плосковыпуклые
плосковогнутые
вогнуто-выпуклые
выпукло-вогнутые
СОБИРАЮЩИЕ
РАССЕИВАЮЩИЕ
Слайд 5Линзы
Теорема об изображении
Если перед линзой находится светящаяся точка S , то
преломления в линзе все лучи(или их продолжения) пересекаются в одной точке S’.
Слайд 6Линзы
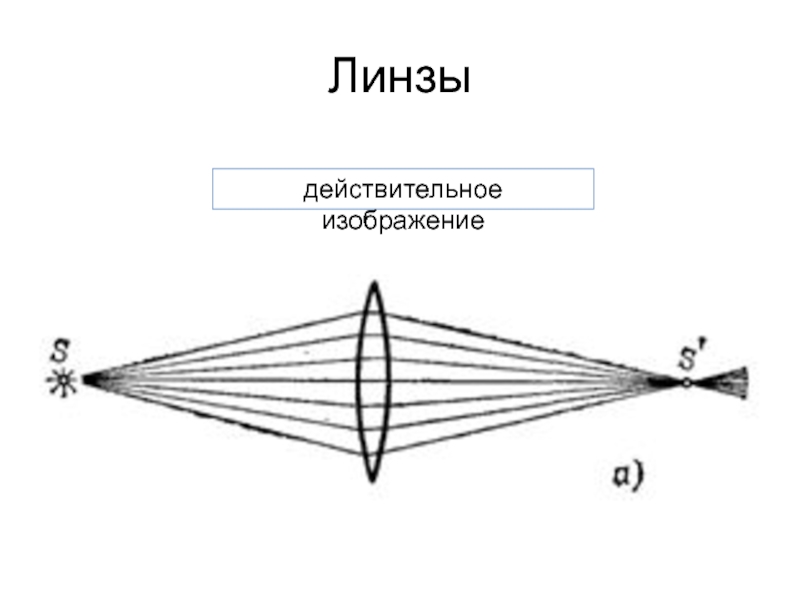
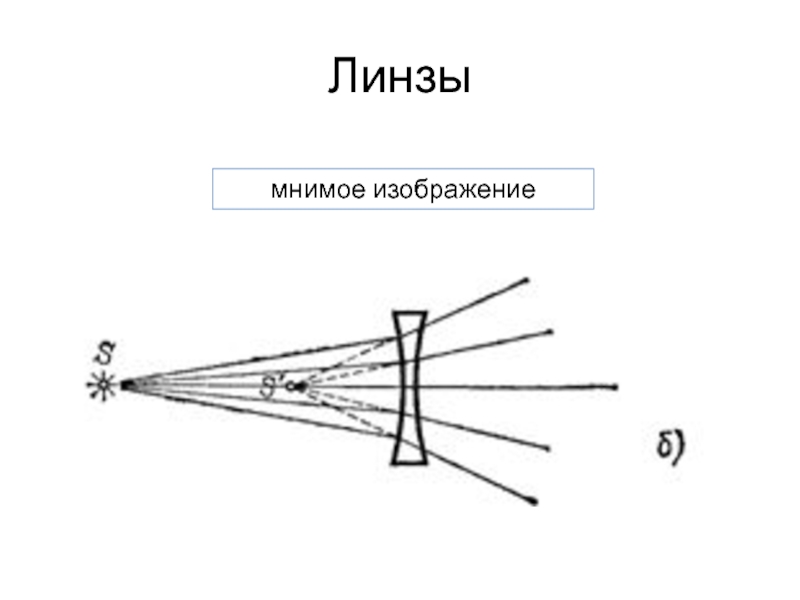
ИЗОБРАЖЕНИЕ
действительное
мнимое
изображение, полученное при пересечении (в точке S’) действительно преломлённых в линзе
Изображение, полученное при пересечении продолжения (в точке S’) преломлённых лучей в обратную сторону.
его видно на экране
его нельзя получить на экране
Слайд 9Построение изображений в линзах
Фокус – точка, в которой собирается параллельный пучок
Фокальная плоскость – плоскость, перпендикулярная оси линзы и представляющая собой геометрическое место фокусов
Фокусное расстояние – расстояние от фокальной плоскости до плоскости линзы.
Оптические оси - прямые, проходящие через оптический центр линзы О.
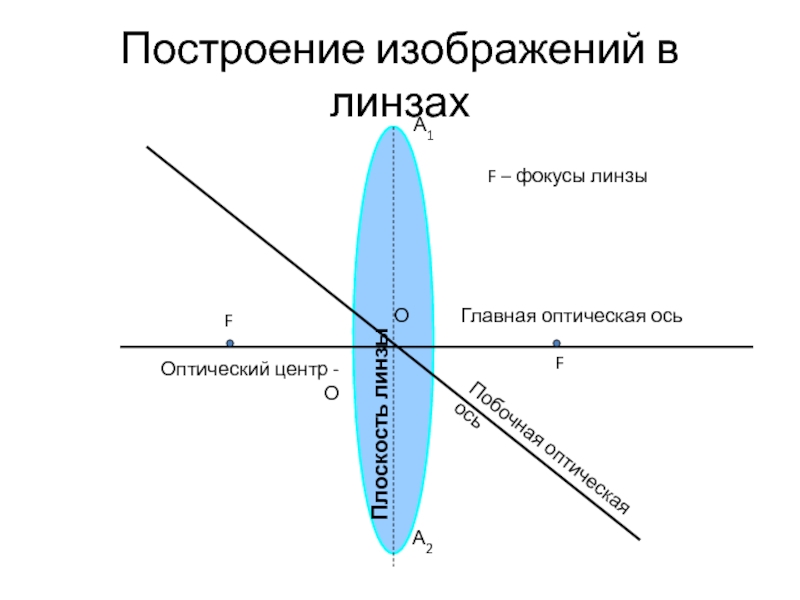
Слайд 11Построение изображений в линзах
При построении изображения светящейся точки или предмета из
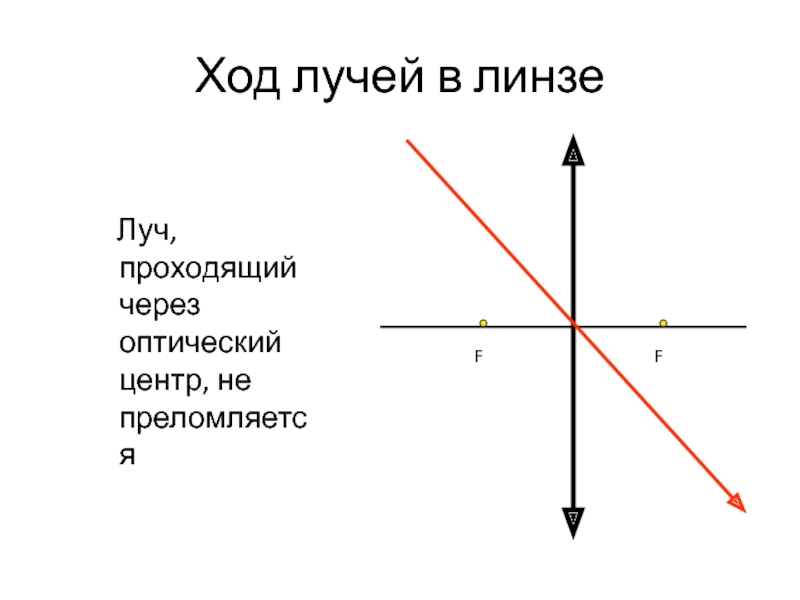
А) луч, проходящий через оптический центр линзы; он проходит через линзу, не преломляясь;
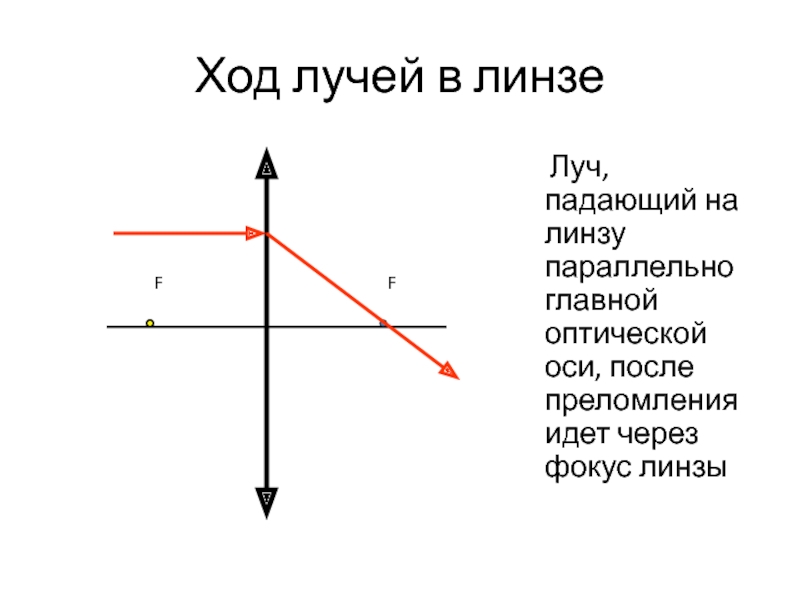
Б) луч, идущий параллельно какой-либо оптической оси; после преломления он проходит через фокус, лежащий на этой оптической оси;
В) луч, проходящий через передний фокус линзы, после преломления должен идти параллельно главной оптической оси;
Г) луч, проходящий через передний двойной фокус, после преломления пройдет через задний двойной фокус.
Слайд 12Построение изображений в линзах
Главная оптическая ось
Побочная оптическая ось
О
Оптический центр - О
F
F
F
А1
А2
Плоскость линзы
Слайд 14Ход лучей в линзе
Луч, падающий на линзу параллельно
F
F
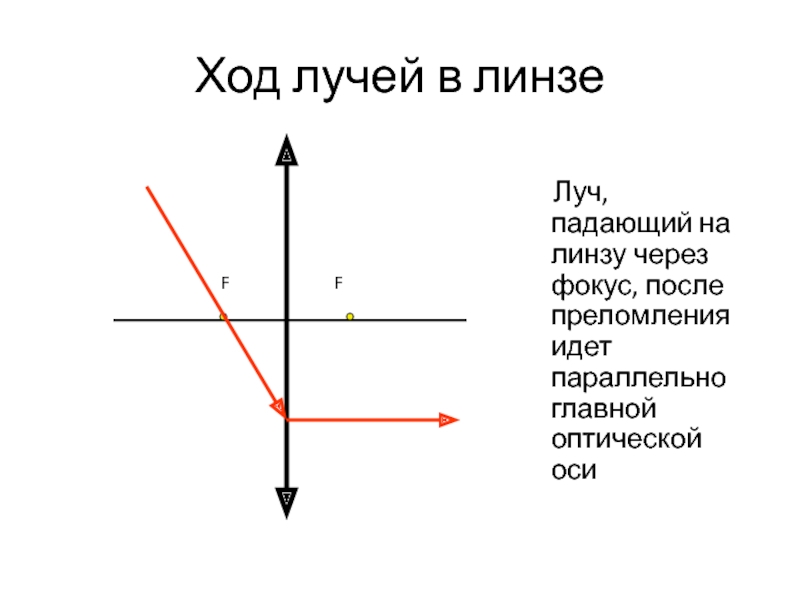
Слайд 15Ход лучей в линзе
Луч, падающий на линзу через
F
F
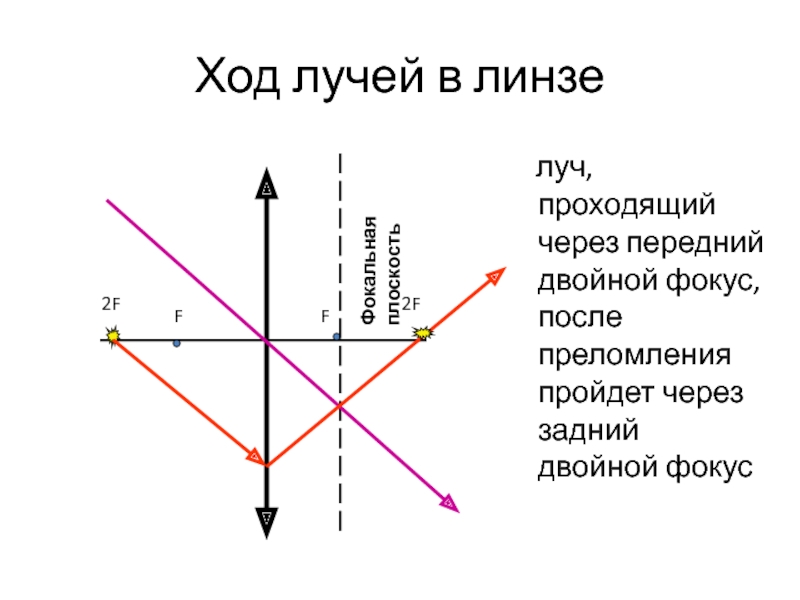
Слайд 16Ход лучей в линзе
луч, проходящий через передний двойной фокус,
Фокальная плоскость
F
F
2F
2F
Слайд 17Ход лучей в линзе
С помощью данных лучей можно построить изображение:
точечного
предмета
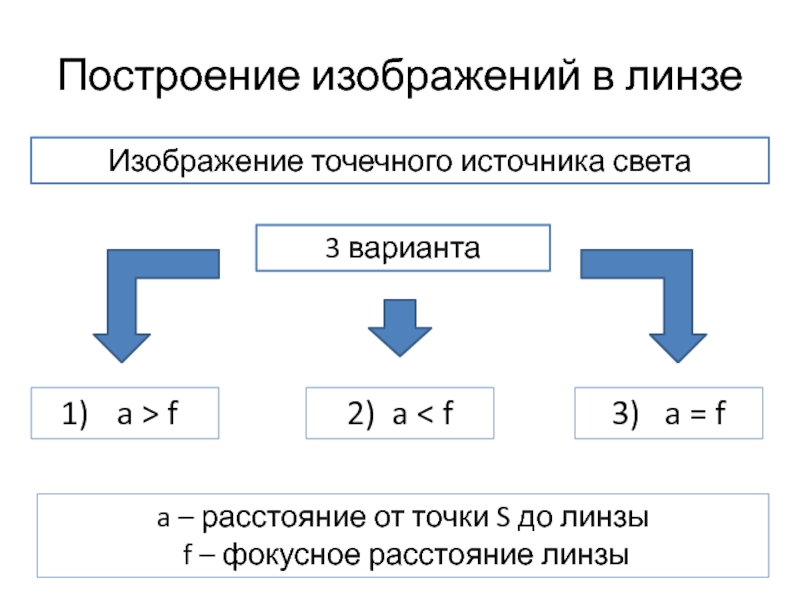
Слайд 18Построение изображений в линзе
Изображение точечного источника света
3 варианта
a > f
2)
3) a = f
a – расстояние от точки S до линзы
f – фокусное расстояние линзы
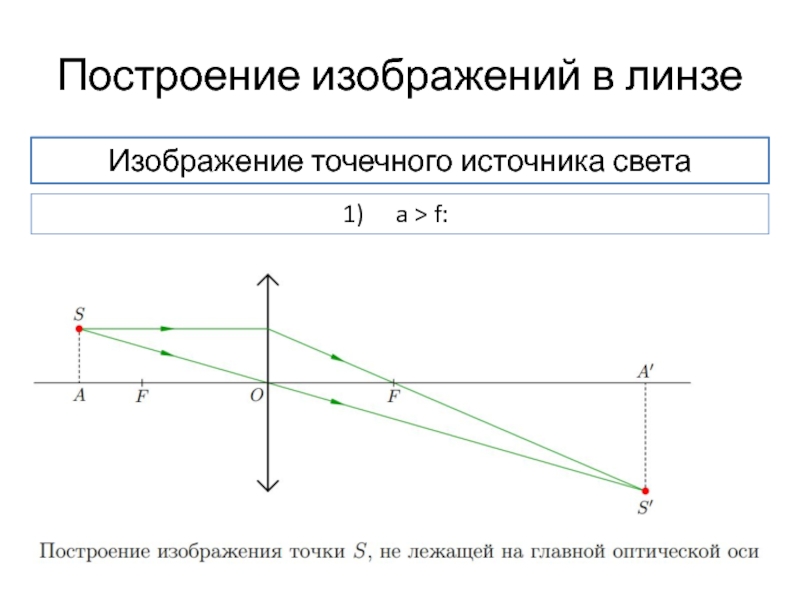
Слайд 19Построение изображений в линзе
Изображение точечного источника света
a > f:
Точечный источник света
Слайд 21Построение изображений в линзе
Изображение точечного источника света
a > f:
Если источник S
луч, идущий через оптический центр линзы — он не преломляется;
луч, параллельный главной оптической оси — после преломления он идёт через фокус.
Слайд 22Построение изображений в линзе
Изображение точечного источника света
a < f:
Точечный источник света
Слайд 23Построение изображений в линзе
Изображение точечного источника света
2) a < f:
S’
Слайд 24Построение изображений в линзе
Изображение точечного источника света
2) a < f:
Если
луч, идущий через оптический центр линзы — он не преломляется;
луч, параллельный главной оптической оси — после преломления он идёт через фокус.
Слайд 25Построение изображений в линзе
Изображение точечного источника света
3) a = f:
Точечный
Слайд 27Построение изображений в линзе
Изображение предмета
1) a > f:
3 ситуации
a) f
b) a = 2f
c) a > 2f
Слайд 28Построение изображений в линзе
Изображение предмета
a) f < a < 2f
Используется
Слайд 30Построение изображений в линзе
Изображение предмета
с) a > 2f
Используется в фотоаппаратах,
Слайд 33Используя лучи
и
примеры построений,
построить изображение в линзе
КРИТЕРИИ ОЦЕНКИ:
2 задания
3 задания – оценка «4»
4 задания – оценка «5»