- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятия о напряжениях презентация
Содержание
- 1. Понятия о напряжениях
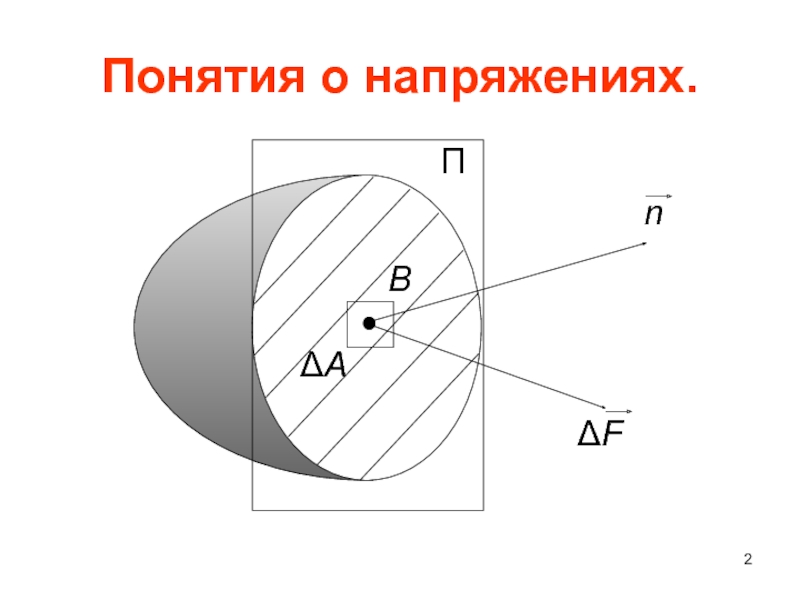
- 2. Понятия о напряжениях. ΔА B
- 3. Выделим в сечении малую площадку ΔА в
- 4. В пределе получаем: где
- 5. Напряжением называется интенсивность внутренней силы в данной
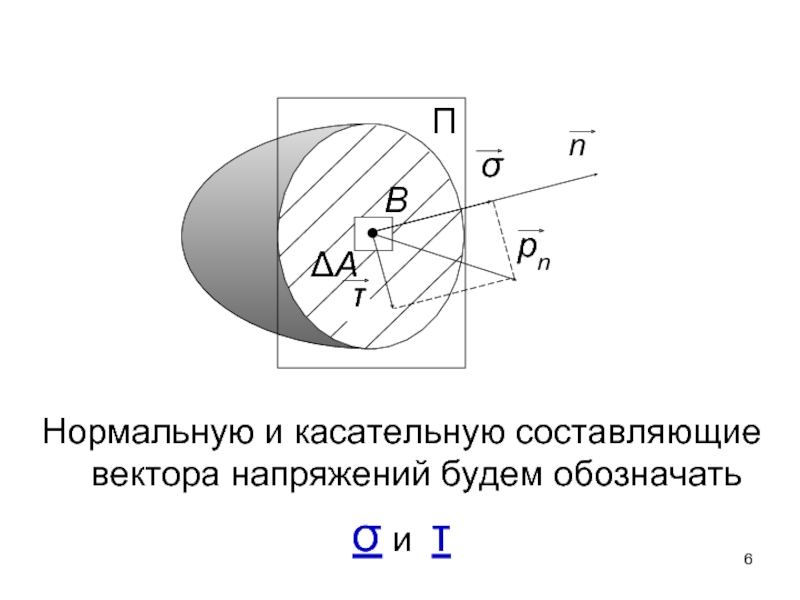
- 6. Нормальную и касательную составляющие вектора напряжений будем
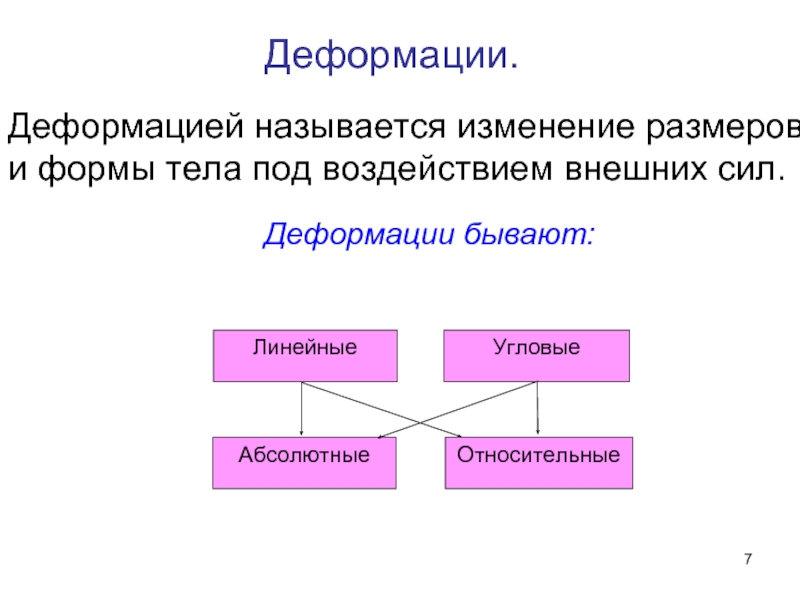
- 7. Деформации. Деформацией называется изменение размеров и формы тела под воздействием внешних сил. Деформации бывают:
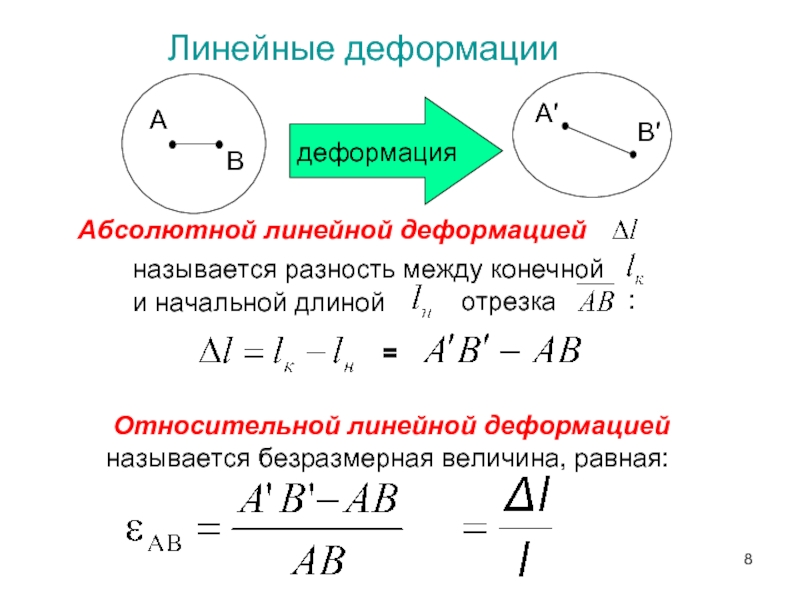
- 8. Линейные деформации Абсолютной линейной деформацией
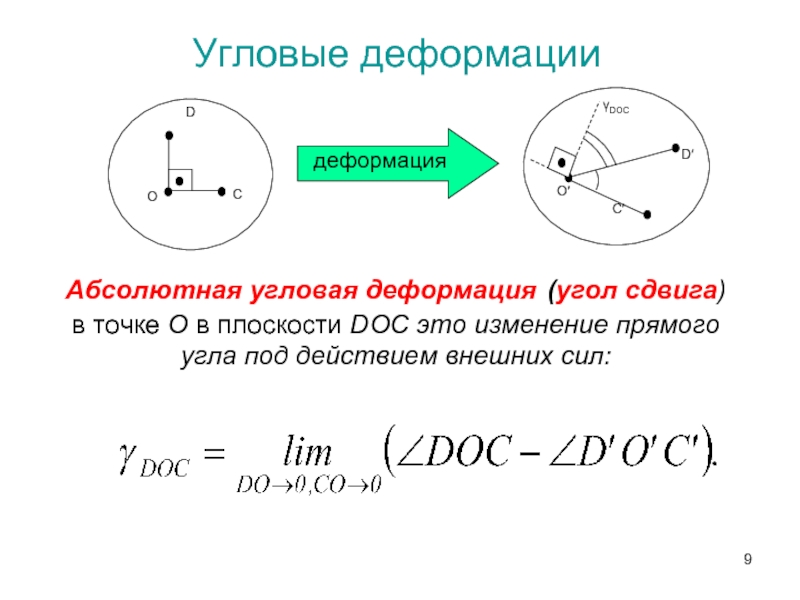
- 9. Угловые деформации Абсолютная угловая деформация
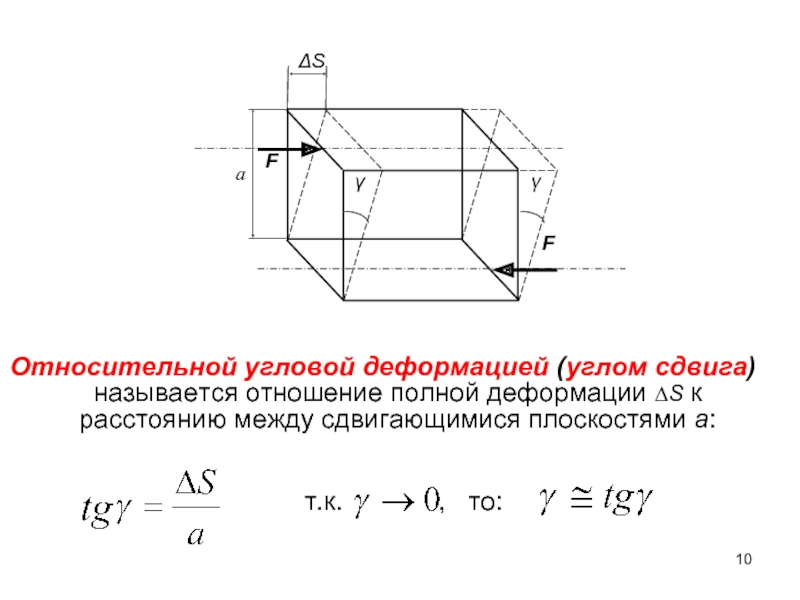
- 10. Относительной угловой деформацией (углом сдвига) называется отношение
- 11. Растяжение – сжатие, это способ
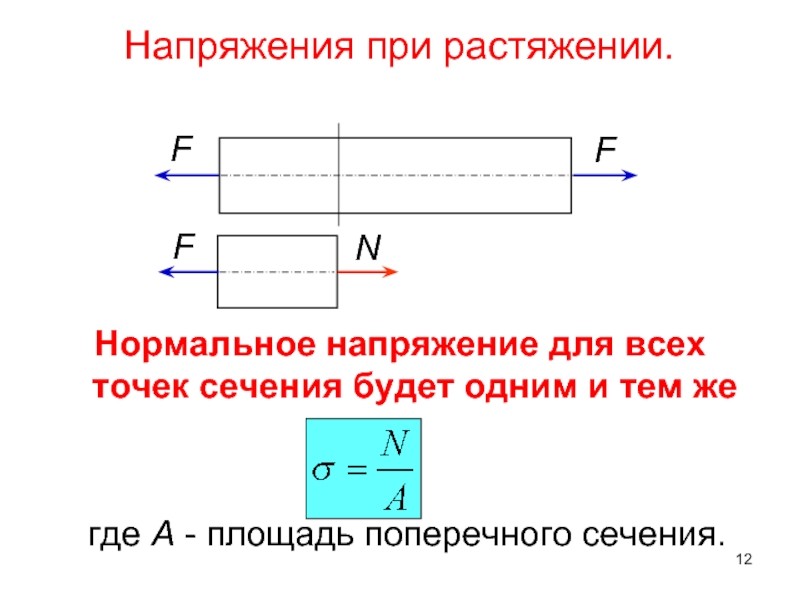
- 12. Нормальное напряжение для всех точек сечения будет
- 13. Закон Гука при растяжении. В упругой области
- 14. где: Е – модуль Юнга – модуль
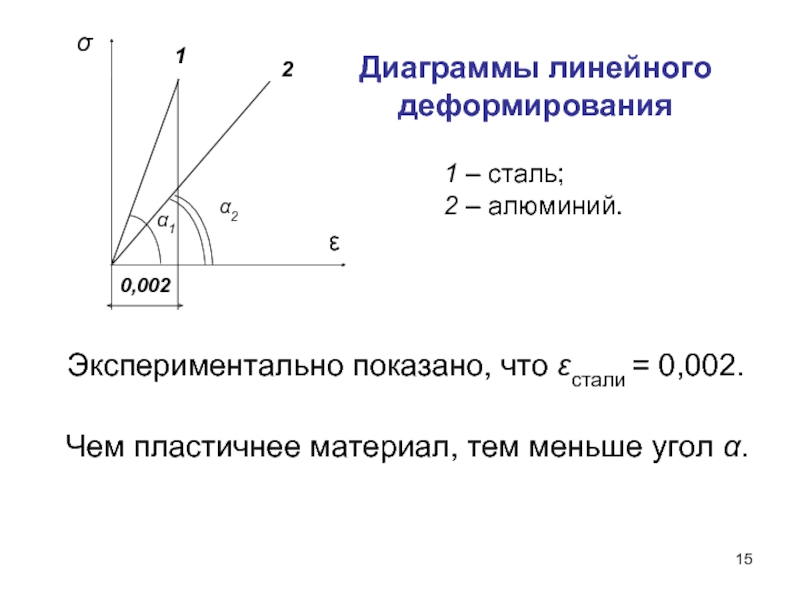
- 15. Диаграммы линейного деформирования 1 –
- 16. Закон Пуассона.
- 17. Отношение поперечной деформации к продольной деформации –
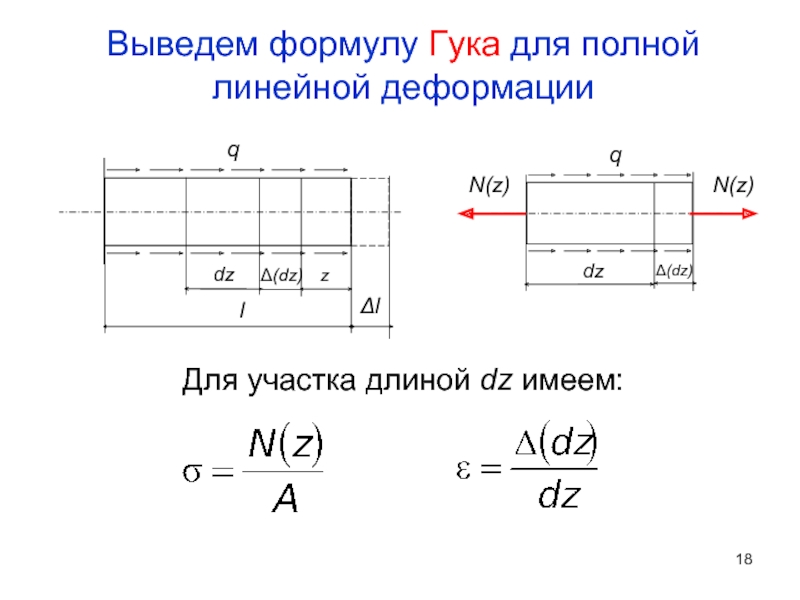
- 18. Выведем формулу Гука для полной линейной деформации
- 19. Подставим эти соотношения в закон Гука:
- 20. Пример: определить удлинение стержня Δl, под воздействием
- 21. Напряжения в наклонных сечениях при растяжении-сжатии Рассмотрим
- 22. т.к. Определим нормальные
- 23. Вывод:
- 24. Статически неопределимые системы при растяжении-сжатии Р
- 25. Изменение длины стержня при нагревании Абсолютное
Слайд 3 Выделим в сечении малую площадку ΔА в окрестности точки B с
Слайд 5 Напряжением называется интенсивность внутренней силы в данной точке поперечного сечения
Напряжение -
интенсивности внутренних сил.
Напряжение, как векторная величина, может быть представлено нормальной и касательной составляющими
(по отношению к площади сечения).
Слайд 7Деформации.
Деформацией называется изменение размеров и формы тела под воздействием внешних сил.
Деформации
Слайд 8Линейные деформации
Абсолютной линейной деформацией
называется разность между конечной
и
отрезка
:
=
Относительной линейной деформацией называется безразмерная величина, равная:
Слайд 9Угловые деформации
Абсолютная угловая деформация (угол сдвига) в точке О в
Слайд 10Относительной угловой деформацией (углом сдвига) называется отношение полной деформации ∆S к
Слайд 11
Растяжение – сжатие, это способ нагружения стержня, при котором внутренние
РАСТЯЖЕНИЕ – СЖАТИЕ ПРЯМОГО БРУСА.
Слайд 12Нормальное напряжение для всех точек сечения будет одним и тем же
где A - площадь поперечного сечения.
Напряжения при растяжении.
Слайд 13Закон Гука при растяжении.
В упругой области нагружения существует прямая пропорциональная зависимость
Слайд 14где: Е – модуль Юнга – модуль продольной упругости (модуль упругости
Размерность:
Естали = 2⋅105 МПа;
Еалюминия = 0,8⋅105 МПа.
ε - относительная линейная упругая
деформация. Величина безразмерная.
Слайд 15
Диаграммы линейного деформирования
1 – сталь;
2 – алюминий.
Экспериментально показано, что εстали =
Чем пластичнее материал, тем меньше угол α.
Слайд 16
Закон Пуассона.
- относительная продольная деформация
- относительная
- показано экспериментально
Слайд 17 Отношение поперечной деформации к продольной деформации – величина постоянная для любого
0 ≤ μ ≤ 0,5
– для любого изотропного материала
μ пробки = 0;
μчугуна = 0,23 ÷ 0,27;
μстали = 0,29 ÷ 0,33;
μмеди = 0,31 ÷ 0,33;
µкаучука = 0,47.
Слайд 19Подставим эти соотношения в закон Гука:
формула Гука для стержня с
формула Гука для стержня с постоянной нормальной нагрузкой
Для стержня, имеющего n различных участков, получаем:
EА - жесткость при растяжении-сжатии
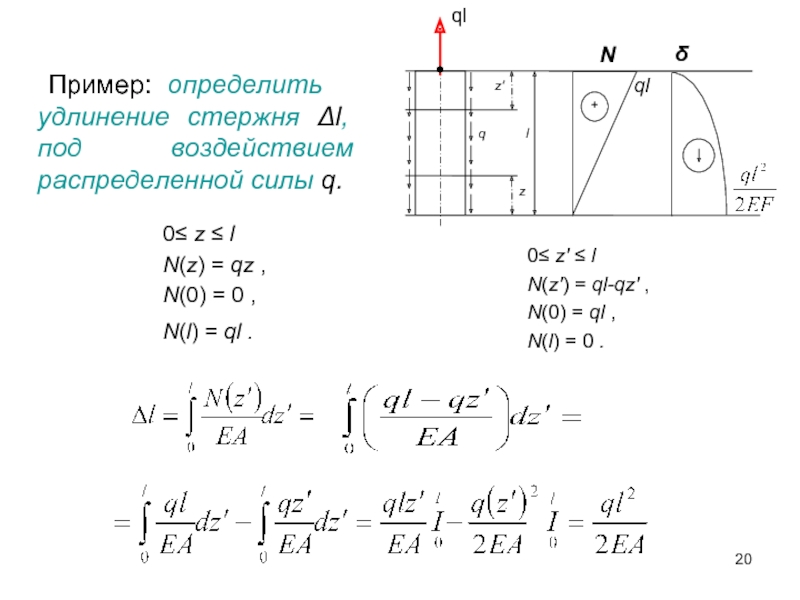
Слайд 20 Пример: определить удлинение стержня Δl, под воздействием распределенной силы q.
0≤ z
N(z) = qz ,
N(0) = 0 ,
N(l) = ql .
0≤ z′ ≤ l
N(z′) = ql-qz′ ,
N(0) = ql ,
N(l) = 0 .
ql
•
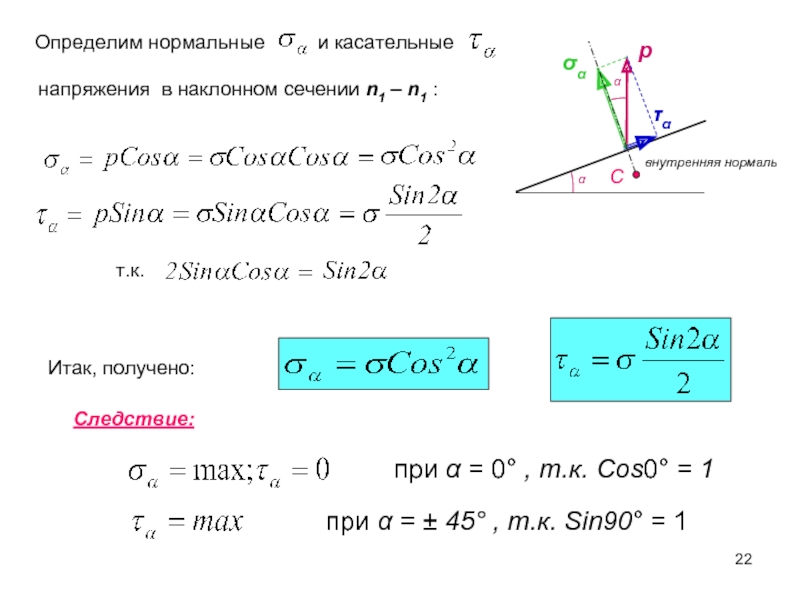
Слайд 21Напряжения в наклонных сечениях при растяжении-сжатии
Рассмотрим стержень, нагруженный растягивающей силой N.
При равномерном распределении сил упругости, полное напряжение р в наклонном сечении будет равно:
α • 0 против хода
часовой стрелки
Тогда площадь наклонного сечения n1 – n1 будет равна:
А – площадь поперечного сечения n0 – n0.
Т.к.
Слайд 22
т.к.
Определим нормальные
и касательные
напряжения в наклонном сечении n1 –
Итак, получено:
при α = 0° , т.к. Cos0° = 1
при α = ± 45° , т.к. Sin90° = 1
Следствие:
Слайд 23
Вывод:
максимальные касательные напряжения возникают на площадках, расположенных под углом 45°
Пример:
разрушение чугунного образца происходит по площадкам максимальных касательных напряжений.
Слайд 24Статически неопределимые системы
при растяжении-сжатии
Р
Ra
Rв
Основное уравнение равновесия
l
l
Дополнительное уравнение
Слайд 25 Изменение длины стержня при нагревании
Абсолютное удлинение стержня длиной
повышении его температуры на определяется
по формуле:
где
линейный коэффициент температурного
расширения материала, (1/град)