- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятия и постулаты термодинамики презентация
Содержание
- 1. Понятия и постулаты термодинамики
- 2. Эпиграф к термодинамике Это хорошо, Ватсон, что
- 3. Возникновение термодинамики Термодинамика, как наука зародилась в
- 4. Николя́ Леона́р Сади́ Карно́ (фр. Nicolas Léonard Sadi
- 5. Развитие термодинамики Развитие термодинамики шло параллельно со
- 6. Исходные понятия термодинамики С точки зрения учения
- 7. Параметры системы Опыт показывает, что состояние термодинамической
- 8. Параметры идеального газа - Объем Объем –
- 9. Параметры идеального газа - Давление С точки
- 10. Давление – Единицы измерения
- 11. Давление – Единицы измерения Миллиме́тр рту́тного столба́
- 12. Параметры идеального газа - Температура Молекулярно-кинетическая теория
- 13. Температура – Шкала Цельсия По шкале Цельсия
- 14. Температура – Шкала Кельвина
- 15. Температура и энергия
- 16. Моль вещества
- 17. Термическое уравнение состояния
- 18. Функции состояния Параметры P,V и T называют
- 19. Равновесные и неравновесные процессы Классическая термодинамика рассматривает
- 20. Равновесные и неравновесные процессы
- 21. Квазистатические процессы для идеального газа Для
- 22. Изохорический процесс Так называются нагрев или охлаждение
- 23. Изобарический процесс В этом процессе газ расширяется
- 24. Изотермический процесс Изотермическим процессом называют квазистатическое расширение
- 25. Первое начало термодинамики
- 26. Теплота Левая часть этого уравнения - δQ
- 27. Теплота Первым термин «калория» применил шведский физик
- 28. Теплота Для справки: Под калорийностью, или энергетической
- 29. Теплота Схема опыта Джоуля представлена на рисунке.
- 30. Теплота Опыт Джоуля повторялся неоднократно. Брались разные
- 31. Внутренняя энергия
- 32. Внутренняя энергия Разница в «значках» при теплоте
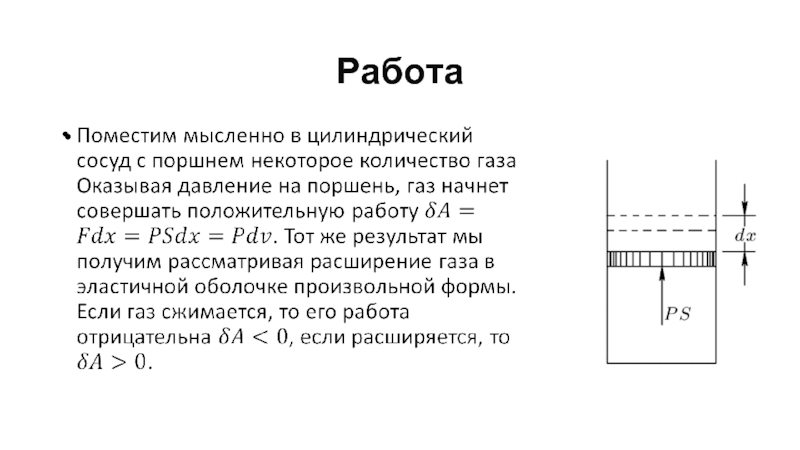
- 33. Работа
- 34. Работа
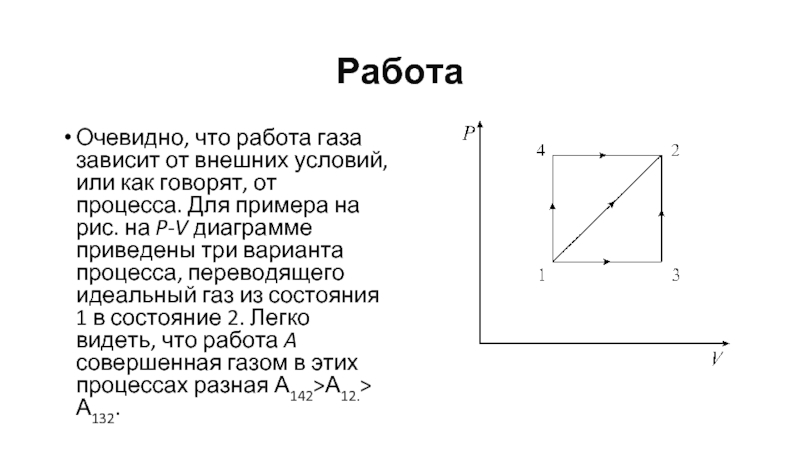
- 35. Работа Очевидно, что работа газа зависит от
- 36. Теплоемкость
- 37. Теплоемкость изохорического процесса
- 38. Теплоемкость изобарического процесса
- 39. Фон Майер, Юлиус Роберт
- 40. Теплоемкость изотермического процесса
- 41. Адиабатический процесс
- 42. Адиабатический процесс
- 43. Адиабатический процесс
- 44. Адиабатический процесс
- 45. Адиабатический процесс
- 46. Работа идеального газа в термодинамических процессах
- 47. Работа идеального газа в термодинамических процессах
- 48. Политропические процессы
- 49. Политропические процессы
- 50. Политропические процессы
- 51. До следующей лекции
Слайд 2Эпиграф к термодинамике
Это хорошо, Ватсон, что Вы меня просветили, но я
Артур Конан Дойль,
Рассказы о Шерлоке Холмсе
Слайд 3Возникновение термодинамики
Термодинамика, как наука зародилась в позапрошлом веке, как наука о
Слайд 4Николя́ Леона́р Сади́ Карно́ (фр. Nicolas Léonard Sadi Carnot); 1 июня 1796 — 24
В 1824 году вышла первая и единственная работа Сади Карно — «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance). Эта работа считается основополагающей в термодинамике. В ней был произведён анализ существовавших в то время паровых машин, и были выведены условия, при которых КПД достигает максимального значения (в паровых машинах того времени КПД не превышал 2 %). Помимо этого там же были введены основные понятия термодинамики: идеальная тепловая машина (см. тепловая машина), идеальный цикл (см. цикл Карно), обратимость и необратимость термодинамических процессов
Слайд 5Развитие термодинамики
Развитие термодинамики шло параллельно со становлением молекулярной физики. Эти разделы
Слайд 6Исходные понятия термодинамики
С точки зрения учения об атомах и молекулах термодинамическая
Слайд 7Параметры системы
Опыт показывает, что состояние термодинамической системы характеризуется небольшим набором параметров.
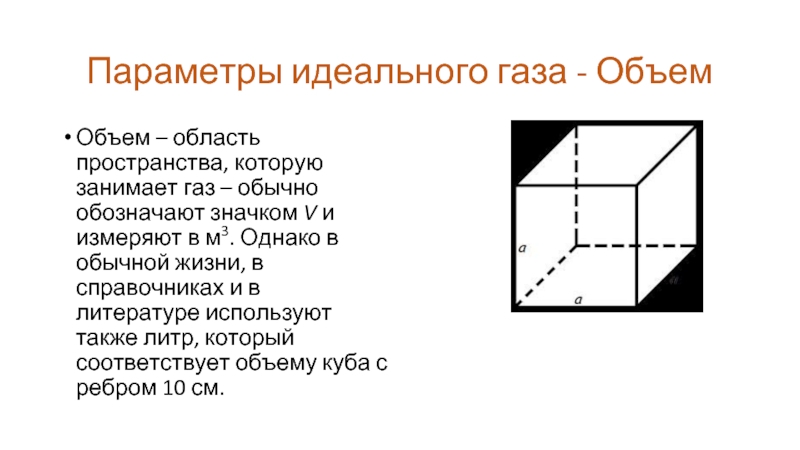
Слайд 8Параметры идеального газа - Объем
Объем – область пространства, которую занимает газ
Слайд 9Параметры идеального газа - Давление
С точки зрения молекулярной физики давление –
Слайд 11Давление – Единицы измерения
Миллиме́тр рту́тного столба́ (русское обозначение: мм рт. ст.;
В Российской Федерации миллиметр ртутного столба допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «медицина, метеорология, авиационная навигация»[1]. Международная организация законодательной метрологии (МОЗМ) в своих рекомендациях относит миллиметр ртутного столба к единицам измерения, «которые могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться, если они не используются»[
Слайд 12Параметры идеального газа - Температура
Молекулярно-кинетическая теория усмотрела глубокую аналогию между средней
Слайд 13Температура – Шкала Цельсия
По шкале Цельсия температура замерзания воды при давлении
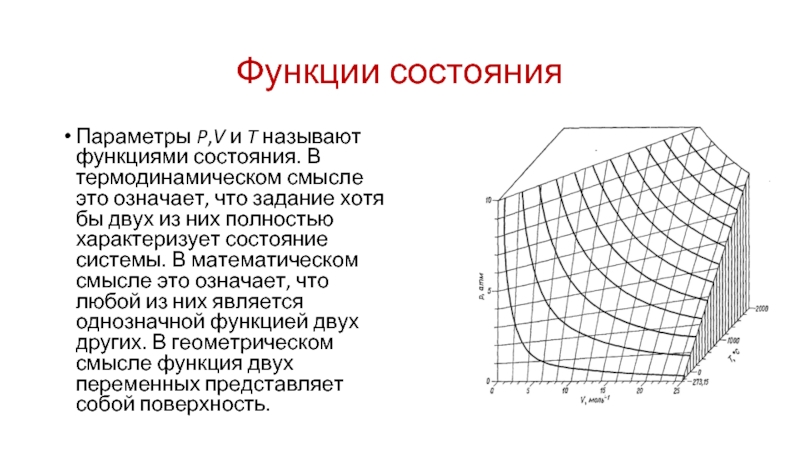
Слайд 18Функции состояния
Параметры P,V и T называют функциями состояния. В термодинамическом смысле
Слайд 19Равновесные и неравновесные процессы
Классическая термодинамика рассматривает только такие изменения состояния системы,
Самопроизвольный переход системы в равновесное состояние называется релаксацией, а время, затраченное на такой переход – временем релаксации. Релаксационные процессы – это процессы выравнивания. Они относятся к неравновесным процессам.
Слайд 21Квазистатические процессы для идеального газа
Для того, чтобы сделать производимые над газом
Слайд 22Изохорический процесс
Так называются нагрев или охлаждение газа при постоянном объеме. На
Слайд 23Изобарический процесс
В этом процессе газ расширяется или сжимается при постоянном давлении.
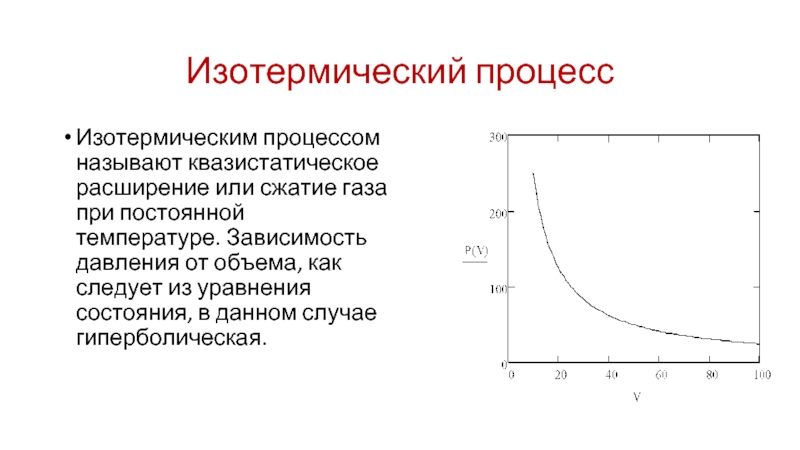
Слайд 24Изотермический процесс
Изотермическим процессом называют квазистатическое расширение или сжатие газа при постоянной
Слайд 26Теплота
Левая часть этого уравнения - δQ – обозначает тепло (бесконечно малую
Слайд 27Теплота
Первым термин «калория» применил шведский физик Иоганн Вильке (1732—1796). Калория определяется,
Слайд 28Теплота
Для справки: Под калорийностью, или энергетической ценностью, пищи подразумевается количество энергии,
Слайд 29Теплота
Схема опыта Джоуля представлена на рисунке. В теплоизолированном сосуде с водой
Слайд 30Теплота
Опыт Джоуля повторялся неоднократно. Брались разные жидкости, разные сосуды и мешалки,
1калория ≈ 4,18 джоулей.