- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Плоские электромагнитные волны. (Лекция 9) презентация
Содержание
- 1. Плоские электромагнитные волны. (Лекция 9)
- 2. ОПРЕДЕЛЕНИЯ В области, достаточно удаленной от вибратора
- 3. Монохроматическая волна. Поляризация. Монохроматической или гармонической волной
- 4. Тогда, направление вектора Е во всех точках
- 5. Уравнение плоской волны Рассмотрим распространение плоской волны
- 6. 2-е уравнение Максвелла В рассматриваемом случае у
- 7. 1-е уравнение Максвелла Подставив Нy m в
- 8. Решение волнового уравнения Назовем коэффициентом распространения Решение этого уравнения имеет вид:
- 9. Коэффициент распространения Возведем в квадрат Получим систему уравнений
- 10. Коэффициент распространения Решая систему уравнений, получим
- 11. Уравнения прямой и отраженной волны для Е.
- 12. Уравнения прямой и отраженной волны для
- 13. Уравнения плоских электромагнитных волн Мгновенное значение вектора Пойнтинга:
- 14. Амплитуды падающей и отраженной волн: Амплитуды волн
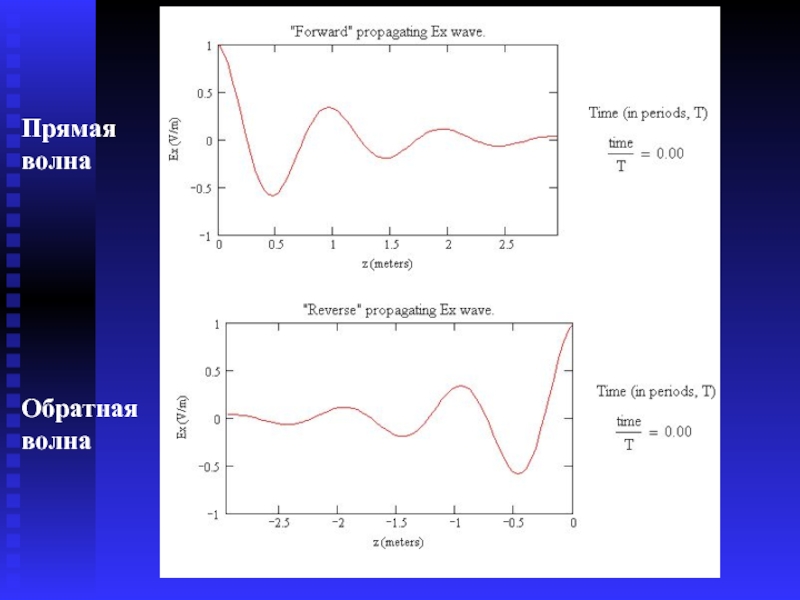
- 15. Прямая волна Обратная волна
- 16. Коэффициент затухания Быстрота затухания зависит от действительной
- 17. Затухание плоской волны При прохождении некоторого расстояния
- 18. Глубина проникновения поля Для среды с высокой
- 19. Волновое сопротивление Волновое сопротивление имеет индуктивный характер.
- 20. Фазовая скорость Фазовой скоростью называется скорость
- 21. Фазовая скорость Фазовой скоростью называется скорость
- 22. Фазовая скорость зависит от частоты. Такие среды называют диспергирующими Фазовая скорость
- 23. Длина волны Это расстояние, на котором фаза
- 24. ВЫВОД -1 В каждой точке поля мгновенное
- 25. ВЫВОД - 2 Направление вектора Е одинаково
- 26. Распространение плоской волны в идеальном диэлектрике Идеальным
- 27. Волновое сопротивление – вещественное число:
- 28. При z = 0 мгновенные значения векторов
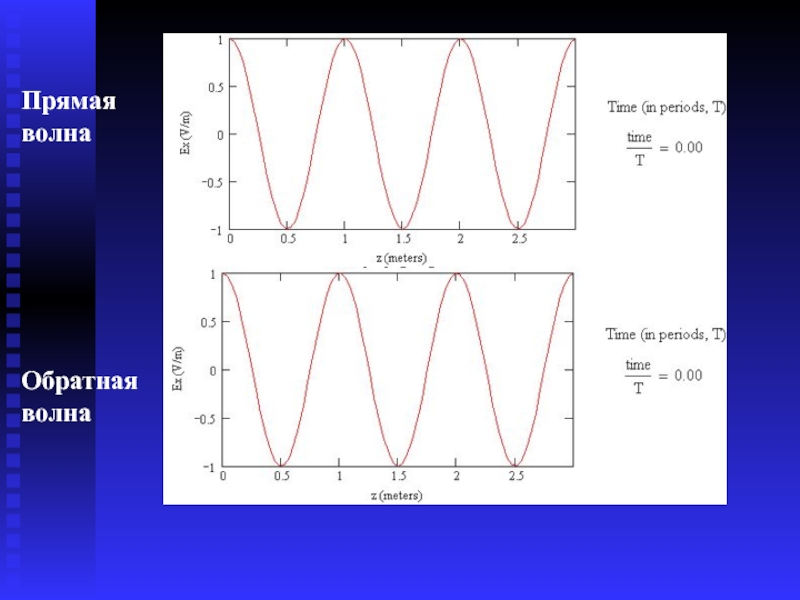
- 29. Прямая волна Обратная волна
- 30. Так как волновое сопротивление – RВ вещественное
ОПРЕДЕЛЕНИЯ В области, достаточно удаленной от вибратора поле имеет волновой характер. Волны называются сферическими, так как поверхности равной фазы
Слайд 2ОПРЕДЕЛЕНИЯ
В области, достаточно удаленной от вибратора
поле имеет волновой характер.
Волны называются сферическими, так как поверхности равной фазы – сферы.
При небольшую часть сферической поверхности можно считать плоской и волну в этой области рассматривать как плоскую.
Плоская волна называется однородной, если векторы поля Е и Н зависят от одной пространственной координаты и времени
Волны называются сферическими, так как поверхности равной фазы – сферы.
При небольшую часть сферической поверхности можно считать плоской и волну в этой области рассматривать как плоскую.
Плоская волна называется однородной, если векторы поля Е и Н зависят от одной пространственной координаты и времени
Слайд 3Монохроматическая волна. Поляризация.
Монохроматической или гармонической волной называется волна, у которой вектора
Е и Н изменяются синусоидально
Если плоская волна линейно поляризована, то направление векторов Е во всем пространстве параллельно друг другу (аналогично – вектор Н).
Слайд 4Тогда, направление вектора Е во всех точках поля одинаково, а углы,
которые вектор Е образует с осями координат – постоянны:
Уравнения однородной линейно поляризованной плоской монохрома-тической электромагнитной волны
Слайд 5Уравнение плоской волны
Рассмотрим распространение плоской волны в однородной среде:
Расположим координатные оси
так, чтобы вектор Е имел только одну проекцию – Ех.
Ех синусоидально зависит только от одной координаты Z и от времени t.
Свободные заряды в рассматриваемом пространстве отсутствуют
Ех синусоидально зависит только от одной координаты Z и от времени t.
Свободные заряды в рассматриваемом пространстве отсутствуют
Слайд 62-е уравнение Максвелла
В рассматриваемом случае у вектора Н только одна проекция
отлична от 0 – Нy . Комплексная амплитуда:
Слайд 71-е уравнение Максвелла
Подставив Нy m в 2-ое уравнение и отбросив индексы
у проекций векторов, получим:
ВОЛНОВОЕ УРАВНЕНИЕ
Слайд 8Решение волнового уравнения
Назовем коэффициентом распространения
Решение этого уравнения имеет вид:
Слайд 11Уравнения прямой и отраженной волны для Е.
Перейдем в уравнении
к мгновенным значениям,
считая, что
Мгновенное значение Е равно сумме ординат прямой и обратной волн. Епад – падающая волна распространяется в сторону возрастающих Z, а отраженная волна в сторону убывания Z
Слайд 12
Уравнения прямой и отраженной волны для Н.
Обозначим волновое сопротивление :
Перейдем к
мгновенным значениям:
Мгновенное значение напряженности магнитного поля равно разности ординат падающей и отраженной волн.
Слайд 14Амплитуды падающей и отраженной волн:
Амплитуды волн затухают в направлении распространения.
Падающая волна
– в направлении оси Z
Отраженная волна - в направлении -Z
Отраженная волна - в направлении -Z
Слайд 16Коэффициент затухания
Быстрота затухания зависит от действительной составляющей коэффициента распространения Г.
Он показывает
уменьшение амплитуды волна при ее распространении
Слайд 17Затухание плоской волны
При прохождении некоторого расстояния l амплитуда волны убывает:
Ослабление, испытываемое
плоской волной принято выражать в неперах или децибелах:
Слайд 18Глубина проникновения поля
Для среды с высокой проводимостью вводят понятие – глубина
проникновения поля.
Это расстояние, при прохождении которого электромагнитное поле ослабевает в е раз
Это расстояние, при прохождении которого электромагнитное поле ослабевает в е раз
Слайд 19Волновое сопротивление
Волновое сопротивление имеет индуктивный характер. Нпад и Нотр отстают соответственно
от Епад и Еотр на угол
Слайд 20
Фазовая скорость
Фазовой скоростью называется скорость перемещения плоскости равных фаз волны:
Фазовая скорость
падающей волны
Слайд 21
Фазовая скорость
Фазовой скоростью называется скорость перемещения плоскости равных фаз волны:
Фазовая скорость
обратной волны
Слайд 24ВЫВОД -1
В каждой точке поля мгновенное значение напряженности электрического поля равно
сумме ординат падающей и отраженной волн.
В каждой точке поля мгновенное значение напряженности магнитного поля равно разности ординат падающей и отраженной волн.
В каждой точке поля мгновенное значение напряженности магнитного поля равно разности ординат падающей и отраженной волн.
Слайд 25ВЫВОД - 2
Направление вектора Е одинаково во всех точках поля и
перпендикулярно к направлению вектора Н.
Оба вектора перпендикулярны к направлению распространения волны.
Плоские волны относятся к классу поперечных электромагнитных волн TEM (Transverse Electro-Magnetic)
Оба вектора перпендикулярны к направлению распространения волны.
Плоские волны относятся к классу поперечных электромагнитных волн TEM (Transverse Electro-Magnetic)
Слайд 26Распространение плоской волны в идеальном диэлектрике
Идеальным называют диэлектрик, у которого проводимость
Рассмотрим
диэлектрик , у которого
Тогда коэффициент поглощения
Коэффициент распространения – мнимое число:
Коэффициент фазы
Тогда коэффициент поглощения
Коэффициент распространения – мнимое число:
Коэффициент фазы
Слайд 27Волновое сопротивление – вещественное число:
Уравнения плоской волны примут вид:
Если среда не
ограниченна в направлении z, то М2=0 и существует только прямая волна.
Распространение плоской волны в идеальном диэлектрике
Слайд 28При z = 0 мгновенные значения векторов поля:
Следовательно амплитуды векторов
поля неизменны. Волна распространяется без затухания, среда непоглощающая.
Вектор Пойнтинга
Вектор Пойнтинга
Распространение плоской волны в идеальном диэлектрике
Слайд 30Так как волновое сопротивление – RВ вещественное число, то волны Е
и Н совпадают по фазе.
Фазовая скорость не зависит от частоты :
Фазовая скорость не зависит от частоты :
Распространение плоской волны в идеальном диэлектрике
