физических, химических и других процессах
Термодинамика базируется на двух основных законах установленных опытным путём.
Первый закон термодинамики характеризует количественную сторону процессов превращения энергии.
Второй закон устанавливает качественную сторону (направленность) процессов, происходящих в физических (термодинамических) системах.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первый закон термодинамики презентация
Содержание
- 1. Первый закон термодинамики
- 2. Отличительной чертой термодинамики является введение в совокупность
- 3. Как известно одним из фундаментальных законов природы
- 4. Термодинамика – это наука о закономерностях превращения
- 5. Под процессом совершения работы понимается такой процесс
- 6. Так как, работа является формой энергии в
- 7. Сказанное можно записать уравнением:
- 8. Для элементарного изменения состояния системы первый закон
- 9. Следует отметить, что термодинамика рассматривает определенные системы,
- 10. Термодинамическая система, внутри которой нет поверхностей раздела,
- 11. Совокупность всех гомогенных частей термодинамической системы, которые
- 12. Для исследования термодинамических систем используется термодинамический метод,
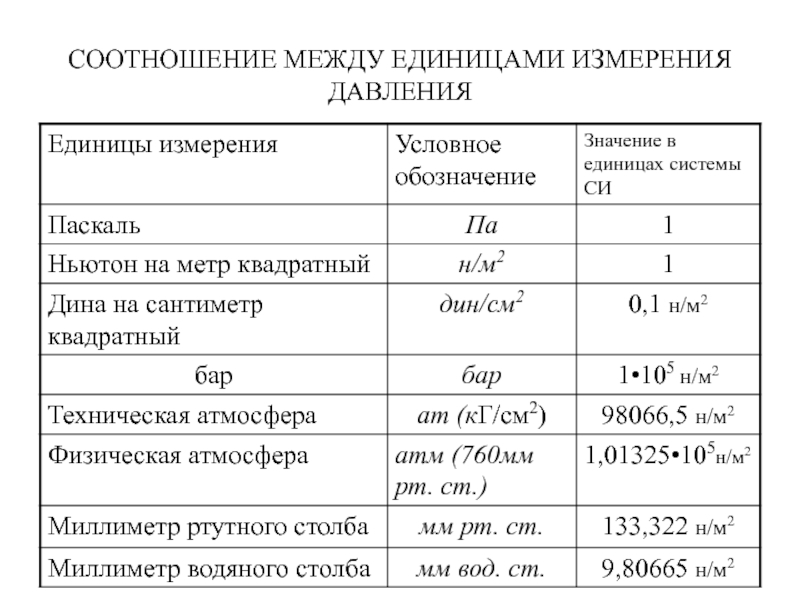
- 13. ПАРАМЕТРЫ СОСТОЯНИЯ Основными параметрами состояния являются давление,
- 14. СООТНОШЕНИЕ МЕЖДУ ЕДИНИЦАМИ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 15. Температура – это физическая величина, характеризующая степень
- 16. Шкала Фаренгейта: за начальную точку отсчёта принята
- 17. Уравнение взаимосвязи давления, температуры, удельного объёма называется
- 18. Для каждого вещества характер функциональной связи между
- 19. Теплоемкость. Классификация, соотношения различных теплоемкостей. Теплоёмкость (истинная
- 20. Функцией состояния Состояния термодинамической системы определяется функцией
- 21. Внутренней энергий U называется энергия системы, зависящая
- 22. Энтальпией Н (теплосодержанием, тепловой функцией) называется функция
- 23. Энтропией S называется функция состояния системы, дифференциал
- 24. Изохорно-изотермическим потенциалом называется характеристическая функция состояния системы
- 25. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ Если изменять внешние условия, в
- 26. Особенности характера каждого из процессов изменения состояния
- 27. Среди различных термодинамических процессов особый интерес представляют
- 28. ИЗОХОРНЫЙ ПРОЦЕСС Изохорический процесс, при котором
- 29. Уравнение состояния идеального газа на изохоре запишется
- 30. Для того чтобы определить параметры состояния 2,
- 31. Работа расширения системы в изохорном процессе равна
- 32. Если воспользоваться понятием о средней теплоемкости cvср,
- 33. Если теплоемкость в рассматриваемом интервале температур постоянна
- 34. ИЗОБАРНЫЙ ПРОЦЕСС Изобарический процесс, протекающий в условиях
- 35. Отсюда следует, что чем выше температура газа,
- 36. Количество теплоты, сообщаемой системе при нагреве (или
- 37. Из очевидного соотношения
- 38. Изменение энтропии в изобарном процессе, т. е. разность
- 39. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС Изотермический процесс, характеризующийся постоянством температуры
- 40. Важно подчеркнуть, что у любых веществ величина
- 41. Как следует из приведенного уравнения, работа системы
- 42. Изменение энтропии в изотермическом процессе, т. е.
- 43. Для идеального газа
- 44. АДИАБАТНЫЙ ПРОЦЕСС Адиабатический процесс, когда тело помещено
- 45. В реальных условиях процесс является адиабатным в
- 46. Течение газа в этом случае будет адиабатным,
- 47. Для определения связи между собой параметров различных
- 48. термических свойств (р и v) в изоэнтропном
- 49. Если в рассматриваемом интервале изменения состояния системы
- 50. Таким образом, для любого состояния системы в
- 51. Для твердых тел и жидкостей k весьма
- 52. Приведенное уравнение справедливо не только для изоэнтропного,
- 54. ПОЛИТРОПНЫЕ ПРОЦЕССЫ Политропными называют термодинамические процессы, удовлетворяющие
- 55. Понятие о политропных процессах было введено в
- 56. Реальные процессы сжатия в газовых двигателях и
- 57. Помимо уже отмеченной нами технической целесообразности введение
- 58. Последнее уравнение справедливо только для изотермического процесса
- 59. Работа расширения системы в политропном процессе между
- 61. Для идеального газа отношение теплоемкости ср к
- 62. Если теплоемкость сп в рассматриваемом интервале параметров
- 63. ДРОССЕЛИРОВАНИЕ. ЭФФЕКТ ДЖОУЛЯ — ТОМСОНА Из опыта
- 64. С процессом дросселирования приходится часто сталкиваться на
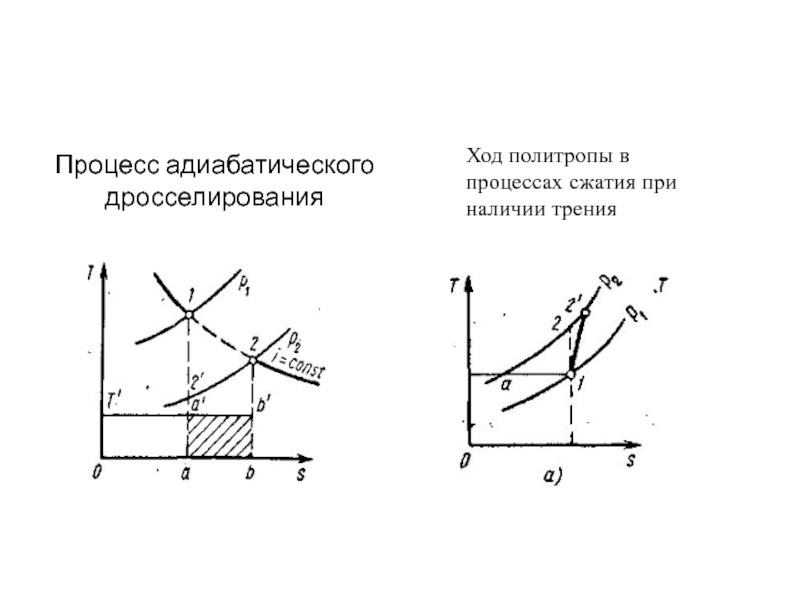
- 65. Процесс адиабатического дросселирования
Слайд 1ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Предметом изучения термодинамики являются закономерности превращения энергии в различных
Слайд 2Отличительной чертой термодинамики является введение в совокупность исследуемых видов энергии внутренней
энергии тел, что собственно и делает термодинамику общей наукой о превращениях энергии.
Любой макроскопический процесс сопровождается изменением внутренней энергии участвующих в процессе, вследствие чего превращение внутренней энергии является наиболее общей особенностью макроскопических процессов. Так если изменение внутренней энергия обусловленное движением составляющих тело частиц, называемым тепловым, то содержание термодинамики можно формулировать как изучение теплового движения. Термодинамика позволяет установить в каком направлении могут протекать различные физические и химические процессы в тех или иных системах. Термодинамика вскрывает связь между различными свойствами вещества.
Слайд 3Как известно одним из фундаментальных законов природы является закон сохранения энергии,
который гласит «энергия не исчезает и не возникает вновь, она лишь переходит из одного вида в другой в различных физических, химических и биологических процессах».
Справедливость положений общего закона сохранения энергии экспериментально для перехода тепловой энергии в другие виды было подтверждено работами Джоуля и других учёных, которыми был установлен принцип эквивалентности теплоты и работы, в соответствии с его содержанием закон называли законом сохранения и превращения энергии.
Закон сохранения и превращения энергии носит название первого закона термодинамики.
Согласно закону сохранения и превращения энергии изменение энергия изолированной системы происходит за счёт изменения внутренней энергии системы в другие виды.
Изменить внутреннюю энергию системы можно двумя способами:
1. Сообщить системе некоторое количество теплоты;
2. Совершить внешними силами над системой работу.
Слайд 4Термодинамика – это наука о закономерностях превращения энергии в теплоту или
работу.
Теплота является одним из наиболее важных понятий термодинамики. Все теплотехнические процессы связаны с преобразование исходной энергии в теплоту или работу.
Изменение теплоты, т.е. её передача или преобразование происходит в процессах теплообмена или совершения работы.
Под процессом теплообмена понимается любой процесс обмена энергией между телами, осуществляющийся путём непосредственного взаимодействия либо между молекулами и атомами этих тел (процесс теплопроводности и конвективного теплообмена), либо между молекулами и атомами одного тела и частицами (фотонами) электромагнитного излучения, испускаемого другими телами (процесс лучистого теплообмена).
Слайд 5Под процессом совершения работы понимается такой процесс взаимодействия какого-либо тела с
другими телами, в результате которого изменяется механическое движение этого тела или его положение по отношению к другим телам. Таковы, например, процессы соударения и их торможение вследствие явления трения, вращение турбины и т.п.
Джоуль своими опытами установил, что между затраченной работой L и количеством полученной теплоты Q существует прямая пропорциональность
Q = АL,
где А – коэффициент пропорциональности. Джоулем было установлено, что коэффициент пропорциональности А всегда сохраняет одно и тоже значение независимо от способа получения теплоты, вида работы, температуры тела и т.д.
Из результатов своих измерений Джоуль определил величину А, которую назвал тепловой эквивалент работы, а обратную ей величину J – механическим эквивалентом теплоты:
А =0,002345 ккал/(кгс•м)
J = 427 кгс•м/ккал
Слайд 6Так как, работа является формой энергии в процессе перемещения под действием
силы.
Действие силы может быть вычислено как произведение внешнего давления и площади, на которую это давление направлено.
Перемещение можно выразить как изменение объёма v рассматриваемой системы, делённое на её поперечное сечение F.
Следовательно, выполненная работа L равна произведению силы рF и перемещению Δv/ F, т.е.
L = (рF)•(Δv/ F) = р•Δv,
где р – постоянное давление, производящее изменение объёма Δv.
Следовательно, когда в результате подвода теплоты к телу температура тела повышается, а вследствие увеличения объёма тела производится внешняя работа, следовательно, подведённая к телу теплота расходуется на изменение внутренней энергии тела U и на совершение работы L.
Слайд 7Сказанное можно записать уравнением:
Q1-2 = ∆U1-2 + L1-2,
где Q1-2 – теплота, сообщённая телу при нагревании от состояния 1 до состояния 2;
∆U1-2 – изменение внутренней энергии тела в том же процессе равное разности внутренних энергий системы в точках 2 и 1;
L1-2 – работа, совершаемая телом в процессе 1-2.
Приведенное уравнение выражает собой математическую запись первого закона термодинамики.
В дифференциальной форме уравнение первого закона термодинамики запишется
dQ = dU + dL,
Исходя из приведенной математической следует, что «тепло, сообщённое системе, расходуется на изменение её внутренней энергии и на совершение системой работы против внешних сил» - формулировка первого закона термодинамики.
Слайд 8Для элементарного изменения состояния системы первый закон термодинамики запишется как
δQ = dU + δA
или
СdТ = dU + δA
где С - теплоёмкость системы; δA – работа равная сумме работы расширения, т.е. работы против внешнего давления, равной рвн dV, и работы δA*, совершаемой системой против других внешних сил:
δA = рвн dV + δA*.
Следует отметить, что работа расширения против сил внешнего давления производится только тогда, когда изменяется объём тела V и когда внешнее давление не равно нулю.
Если же V сохраняется постоянным, то какие бы изменения ни претерпевали другие параметры, характеризующие состояние тела, работа расширения равна нулю.
Таким образом, с точки зрения возможности совершения телом (системой) работы против сил р с параметр V является связанный с этой силой.
Слайд 9Следует отметить, что термодинамика рассматривает определенные системы, так называемые термодинамические системы.
Под термодинамической системой понимают совокупность макроскопических объектов (тел и полей), обменивающихся энергией в форме работы и в форме тепла как с друг другом, так и с внешней средой, т.е. с внешними по отношению к системе телами и полями.
Термодинамическая система называется замкнутой или изолированной, если отсутствует всякий обмен энергией между нею и внешней средой. Система называется изолированной в тепловом отношении или адиабатические изолированной, если отсутствует теплообмен между нею и окружающей средой. Термодинамическая система, обменивающая энергией с внешней средой только путём теплообмена, называется изолированной в механическом отношении.
Слайд 10Термодинамическая система, внутри которой нет поверхностей раздела, отделяющих друг от друга
макроскопические части системы, различающихся по своим свойствам и составу, называется гомогенной.
Термодинамическая система, не удовлетворяющая этому условию, называется гетерогенной. Примерами гетерогенных систем являются: тающий лёд, влажный пар, сплавы.
Система называется физически однородной, если её состав и физические свойства одинаковы для всех макроскопических частей этой системы, равных по объёму.
Состояние системы называют стационарным, если оно не изменяется во времени. Стационарное состояние системы называется равновесным, если его неизменность во времени не обусловлена протеканием какого-либо внешнего по отношению к системе процесса.
Слайд 11Совокупность всех гомогенных частей термодинамической системы, которые в отсутствие внешнего силового
воздействия являются физически однородными, называется фазой.
Различные вещества, входящие в термодинамическую систему, наименьшее число которых достаточно для образования всех фаз системы, называются компонентами (независимыми компонентами).
Гомогенная система, состоящая из двух и большего числа химически чистых веществ, называется раствором.
Один из компонентов раствора (обычно тот, который содержится в наибольшем количестве) называется растворителем, а остальные компоненты – растворёнными веществами.
Слайд 12Для исследования термодинамических систем используется термодинамический метод, суть которого заключается в
изучении свойств системы взаимодействующих тел путём анализа условий и количественных соотношений происходящих в системе превращений энергии.
Термодинамический метод используется для теоретического анализа общих закономерностей самых разнообразных явлений.
Для того чтобы анализировать выбранную термодинамическую систему необходимо конкретные физические условия, в которых находится вещество в системе, т.е. мы должны знать совокупность параметров которые характеризуют макроскопические свойства системы.
Такие параметры называются термодинамическими параметрами или параметрами состояния.
Слайд 13ПАРАМЕТРЫ СОСТОЯНИЯ
Основными параметрами состояния являются давление, температура и удельный (или молярный)
объём.
Давлением называется физическая величина р, равная отношению численного значения нормальной силы ∆Fn, действующей на участок поверхности тела площадью ∆S, к величине ∆S, стремящейся к нулю. р = (dF / dS) Единицы измерения давления:
в системе СИ– н/м², бар, мм рт. ст.;
внесистемной - мм. вод. ст., техническая атмосфера – ат. или кГ/см², физическая атмосфера – атм. Паскаль (Па) – давление, вызванное силой 1 ньютон (Н), равномерно распределённой по нормали к ней поверхности площадью 1 м2. Ньютон – сила, сообщающая телу массой 1 кг ускорением кг/с2.
Давлением называется физическая величина р, равная отношению численного значения нормальной силы ∆Fn, действующей на участок поверхности тела площадью ∆S, к величине ∆S, стремящейся к нулю. р = (dF / dS) Единицы измерения давления:
в системе СИ– н/м², бар, мм рт. ст.;
внесистемной - мм. вод. ст., техническая атмосфера – ат. или кГ/см², физическая атмосфера – атм. Паскаль (Па) – давление, вызванное силой 1 ньютон (Н), равномерно распределённой по нормали к ней поверхности площадью 1 м2. Ньютон – сила, сообщающая телу массой 1 кг ускорением кг/с2.
Слайд 15Температура – это физическая величина, характеризующая степень нагретости тела т.е. температура
характеризует тепловое состояние тела.
Измерение температуры можно производить только косвенным путём, основываясь на сравнительных величинах физических свойств тела, которые можно непосредственно замерить.
Применяемые для этой цели устройства называются термометрами, а устанавливаемая с их помощью шкала температуры – эмпирической. За начальную в эмпирических температурных шкалах принимаются характерные точки используемых веществ.
Шкала Цельсия (сто градусная шкала) – за начальную точку отсчёта (tо =0ºС) принята точка перехода воды в твёрдое состояние (лёд), за конечную – кипение воды
(tк =100ºС) при 1 атмосфере.
Слайд 16Шкала Фаренгейта: за начальную точку отсчёта принята (tо =32ºF = 0ºС),
за конечную – (tк = 212ºF=100ºС).
Шкала Кельвина. За начальную точку отсчёта температуры принимается точка, когда отсутствует движение молекул и атомов. Эту температуру называют абсолютным нулём, а шкалу абсолютной. ТоºК = tºС + 273,15ºС.
Удельный объём вещества (v) представляет собой объём, занимаемый единицей массы вещества.
Удельный объём связан с массой вещества G и его объёмом V соотношением v = V / G.
Удельный объём измеряется в м3/ кг или см3/г.
Слайд 17Уравнение взаимосвязи давления, температуры, удельного объёма называется уравнением состояния.
рv = RT,
где R – универсальная газовая постоянная, численно равна работе, совершаемая 1 молем идеального газа при изобарном нагреве (при постоянном давлении) на один градус.
При отсутствии внешних воздействий на систему состояния чистого вещества экспериментально установлено, если заданы два независимых параметра состояния любой другой параметр является однозначной функцией двух заданных параметров. Поскольку все параметры состояния «равноправные» при определении состояния вещества, то их взаимосвязь можно записать соотношениями:
Т = φ(р,v); р = ψ(Т,v); v = f(р,Т).
Слайд 18Для каждого вещества характер функциональной связи между р, v и Т
индивидуален и, следовательно, термодинамические свойства описываются своим уравнением состояния.
Связь между параметрами состояния может быть представлена в системе координат в виде так называемой термодинамической поверхности. В практических расчётах чаще всего термодинамические поверхности в системе координат на плоскости, в которых используются какие-либо два (из трёх) параметров состояния. При этом значение третьего параметра определяют для каждой пары заданных параметров из уравнения состояния или из эксперимента. Такого рода системы координат называют диаграммами состояния вещества. Например, р, v – диаграмма, v,Т – диаграмма и другие.
Слайд 19Теплоемкость. Классификация, соотношения различных теплоемкостей.
Теплоёмкость (истинная теплоёмкость) вещества называется отношение элементарного
количества тепла δQ, сообщённого телу в каком-либо процессе, к соответствующему изменению температуры вещества.
С = (δQ/dT)
или
С = Q /(Т2 – Т1)
Теплоёмкость зависит от массы тела, его химического состава и вида процесса.
Общее выражение для элементарного количества теплоты. Если известны аналитические выражения для внутренней энергии или энтальпии тела в виде функций параметров состояния, то при помощи первого начала термодинамики
Слайд 20Функцией состояния
Состояния термодинамической системы определяется функцией состояния – это такая физическая
характеристика системы, изменение которой при переходе системы из одного состояние в другое не зависит от вида соответствующего этому переходу термодинамического процесса, а целиком определяется значениями параметров начального и конечного состояний.
Такими функциями являются: внутренняя энергия, энтальпия, энтропия, изохорно-изотермический потенциал, изобарно-изотермический потенциал.
Такими функциями являются: внутренняя энергия, энтальпия, энтропия, изохорно-изотермический потенциал, изобарно-изотермический потенциал.
Слайд 21Внутренней энергий U называется энергия системы, зависящая только от её термодинамического
состояния.
Внутренняя энергия системы равна сумме:
а) кинетической энергии хаотического движения микрочастиц системы (молекул, атомов, илнов, свободных электронов и др.);
б) потенциальной энергии взаимодействия этих частиц;
в) энергии взаимодействия атомов или ионов в молекулах;
г)энергии электронных оболочек атомов и ионов;
д) внутриядерной энергии;
е) энергии электромагнитного излучения.
Слайд 22Энтальпией Н (теплосодержанием, тепловой функцией) называется функция состояния термодинамической системы, равная
сумме её внутренней энергии и произведения давления на объём системы, выраженной в тех же единицах:
Н = U + pV.
Энтальпия идеального газа зависит только от его абсолютной температуры и пропорциональна массе газа.
Энтальпия смеси идеальных газов равна сумме энтальпий всех газов, входящих в состав смеси.
Изоэнтальпийным называется термодинамический процесс, в котором энтальпия системы остаётся не изменой.
Слайд 23Энтропией S называется функция состояния системы, дифференциал которой в элементарном обратимом
процессе равен отношению бесконечно малого количества тепла, сообщённого системе, к абсолютной температуре последней:
dS = δQ /Т.
Энтропия сложной системы равна сумме всех её однородных частей.
Изоэнтропийным процессом называется термодинамический процесс, в котором энтропия системы не изменяется.
Энтропия физически однородной системы является функцией двух независимых параметров состояния.
Слайд 24Изохорно-изотермическим потенциалом называется характеристическая функция состояния системы
F = U –ТS при независимых переменных Т и V.
Изобарно-изотермическим потенциалом называется характеристическая функция состояния системы Ф = Н –ТS = U + pV - ТS при независимых переменных
Т и р.
Слайд 25ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
Если изменять внешние условия, в которых находится термодинамическая система, то
будет изменяться и состояние системы, т.е. термодинамические параметры, характеризующие состояние системы, будут иметь в разные моменты времени различные значения.
Последовательность изменений состояния системы составляет термодинамический процесс. Всякий процесс изменения состояния системы представляет собой отклонение от состояния равновесия. Нарушение равновесия приводит к возникновению внутри системы процессов, противодействующих отклонению от состояния равновесия. Этими внутренними процессами, компенсирующими нарушение равновесия и восстанавливающими его, являются элементарные процессы обмена энергией при столкновении составляющих тело элементарных частиц — молекул, ионов, электронов.
Последовательность изменений состояния системы составляет термодинамический процесс. Всякий процесс изменения состояния системы представляет собой отклонение от состояния равновесия. Нарушение равновесия приводит к возникновению внутри системы процессов, противодействующих отклонению от состояния равновесия. Этими внутренними процессами, компенсирующими нарушение равновесия и восстанавливающими его, являются элементарные процессы обмена энергией при столкновении составляющих тело элементарных частиц — молекул, ионов, электронов.
Слайд 26Особенности характера каждого из процессов изменения состояния тела определяются теми конкретными
физическими условиями, в которых протекает данный процесс. Простейшими процессами являются: изотермический процесс, характеризующийся постоянством температуры тела во время процесса (Т = const); изобарический процесс, протекающий в условиях постоянного давления на тело (р = const);
изохорический процесс, при котором объем тела остается в течение всего, процесса неизменным (V = const); адиабатический процесс, когда тело помещено в теплоизолирующую оболочку, не допускающую теплообмена между телом и окружающей средой.
В общем виде термодинамический процесс характеризуется условием X — const, где X — один из внешних или внутренних параметров системы или некоторая функция их.
Слайд 27Среди различных термодинамических процессов особый интерес представляют так называемые замкнутые или
круговые процессы, при которых система, пройдя через ряд последовательных состояний, возвращается к исходному, или начальному состоянию. Круговой процесс называют также циклом.
Равновесные процессы изменения состояния характеризуются определенными значениями термодинамических параметров и поэтому допускают графическое изображение.
Слайд 28ИЗОХОРНЫЙ ПРОЦЕСС
Изохорический процесс, при котором объем тела остается в течение всего,
процесса неизменным (V = const). Рассмотрим изохорный процесс, осуществляемый от состояния 1, в котором рабочее тело имеет давление р1 температуру T1 и объем V, до состояния 2.
Слайд 29Уравнение состояния идеального газа на изохоре запишется рV = RT отсюда
(р/Т) = const следовательно для процесса 1-2 будем иметь (р1 / Т1) = (р2 / Т2) или
p2 / р1 = Т2 / Т1.
В идеальном газе повышение температуры (нагрев газа) в сосуде постоянного объема всегда приводит к росту давления, причем давление растет тем быстрее, чем меньше значение v на данной изохоре (это следует из гиперболического характера изотермы идеального газа в
р, v -диаграмме).
Нагрев реальных газов и жидкостей также приводит к росту давления, причем давление в жидкости растет значительно быстрее, чем в газе.
Особенность, присущую изохорам воды при низких температурах, а именно, при температуре 3,98 0С плотность воды при атмосферном давлении проходит через максимум.
Слайд 30Для того чтобы определить параметры состояния 2, нужно знать один из
параметров в точке 2 (например, давление р2 или температуру Т2 и т. д.).
Поскольку состояние изменяется по изохоре, следовательно, оказывается заданным еще один параметр состояния — объем V.
Зная V и Т2 (или V и р2, или V и S2 и т.д.), с помощью диаграмм состояния, таблиц термодинамических свойств данного вещества или уравнения состояния можно определить все остальные параметры, характеризующие состояние рабочего тела в точке 2.
Слайд 31Работа расширения системы в изохорном процессе равна нулю. Из соотношения
l1-2 = ∫ р dv ,
очевидно, что для изохорного процесса, когда v = const,
l1-2 = 0.
Количество теплоты, сообщаемой системе при нагреве в изохорном процессе, определяется из уравнения первого закона термодинамики dq = du + р dv, так как для изохорного процесса dv = 0, то dq = du и, следовательно, количество теплоты, сообщаемой системе при нагреве от состояния 1 (параметры этого состояния v, Т1) до состояния 2 (параметры v, Т2), равно разности внутренних энергий и2 и и1:
q2-1 = u2 (v, Т2) - u1 (v, Т1).
После некоторых преобразований можно получить следующее соотношение:
Т2
q2-1 = ∫ сv dT.
Т1
Слайд 32Если воспользоваться понятием о средней теплоемкости cvср, то это соотношение можно
представить в следующем виде:
q2-1 = cvср (Т2-Т1).
Наконец, для случая, когда теплоемкость в рассматриваемом интервале температур постоянна, имеем:
q2-1 = cv (Т2-Т1).
Изменение энтропии в изохорном процессе определяется следующим образом. Из соотношения
Т2 Т2
s2 (v, Т2) - s1 (v, Т1) = ∫ [(∂s /∂T)]v dT = ∫ [(cv /T)]v dT
Т1 Т1
Располагая значениями теплоемкости Располагая значениями теплоемкости cv нетрудно с помощью этого соотношения подсчитать изменение энтропии в изохорном процессе.
Слайд 33Если теплоемкость в рассматриваемом интервале температур постоянна (и, следовательно, cv можно
вынести за знак интеграла), получаем
s2 (v, Т2) - s1 (v, Т1) = cv ℓn(Т2 /T1),
т. е. зависимость энтропии от температуры, на изохоре имеет логарифмический характер.
Слайд 34ИЗОБАРНЫЙ ПРОЦЕСС
Изобарический процесс, протекающий в условиях постоянного давления на тело (р
= const).
Если изобарный процесс в системе осуществляется от состояния 1 до состояния 2 и если известны параметры системы в состоянии 1, то для того чтобы определить параметры системы в состоянии 2, нужно знать один из параметров системы в точке 2 (второй параметр — давление— известен); другие параметры состояния системы в точке 2 могут быть определены с помощью диаграмм состояния, уравнения состояния или таблиц термодинамических свойств вещества так же, как и для изохорного процесса.
Параметры состояния идеального газа на изобаре связаны соотношением:
(v2 / v1)= (Т2 / Т1)
Если изобарный процесс в системе осуществляется от состояния 1 до состояния 2 и если известны параметры системы в состоянии 1, то для того чтобы определить параметры системы в состоянии 2, нужно знать один из параметров системы в точке 2 (второй параметр — давление— известен); другие параметры состояния системы в точке 2 могут быть определены с помощью диаграмм состояния, уравнения состояния или таблиц термодинамических свойств вещества так же, как и для изохорного процесса.
Параметры состояния идеального газа на изобаре связаны соотношением:
(v2 / v1)= (Т2 / Т1)
Слайд 35Отсюда следует, что чем выше температура газа, тем больше его удельный
объем (т. е. тем меньше плотность). При этом величина v на изобаре при повышении температуры растет тем быстрее, чем меньше давление.
Для реальных газов, жидкостей и твердых тел при нагреве также имеет место термическое расширение вещества на изобаре (за исключением некоторых аномальных областей состояния вроде упомянутой области аномалии воды при низких температурах).
При этом, как известно, при увеличении температуры на одно и то же значение газ расширяется гораздо больше, чем жидкость или твердое тело.
Работа расширения системы в изобарном процессе определяется следующим образом:
l1-2 = ∫ р dv = p(v2-v1).
Для идеального газа это соотношение может быть представлено также и в следующем виде:
l1-2 = R (Т2 - Т1)
Слайд 36Количество теплоты, сообщаемой системе при нагреве (или отдаваемой системой при охлаждении)
в изобарном процессе, определяется следующим образом. Из уравнения первого начала термодинамики, записанного в виде
dq = dh — v dp,
следует, что для изобарного процесса (dp=0) dq = dh и, следовательно, количество теплоты, сообщаемой системе при нагреве от состояния 1 (имеющего параметры p,T1) до состояния 2 (с параметрами р, Т2), равно разности энтальпий h2 и h1 в этих состояниях:
q2-1 = h2 (р, Т2) - h1 (р, Т1).
Значения h1 и h2, необходимые для вычисления q2-1 могут быть найдены из таблиц термодинамических свойств данного вещества или из диаграмм состояния этого вещества.
В свою очередь разность энтальпий двух состояний на изобаре может быть также выражена следующим образом.
Слайд 37Из очевидного соотношения
Т2 Т2
h2 (р, Т2) - h1 (р, Т1) = ∫ [(∂h /∂T)]р dT = ∫ cр dT
Т1 Т1
Отсюда следует, что выражение для количества теплоты в изобарном процессе может быть записано следующим образом:
Т2
q2-1 = ∫ cр dT
Т1
или, что то же самое,
q2-1 = cрср (Т2-Т1).
где cvср — средняя теплоемкость сР в интервале температур
Т1 —Т2.
Если ср не зависит от температуры, то
q2-1 = cр (Т2-Т1).
Слайд 38Изменение энтропии в изобарном процессе, т. е. разность энтропий, соответствующих состояниям 1 и
2, определяется из соотношения
Т2 Т2
s2 (р, Т2) - s1 (р, Т1) = ∫ [(∂s /∂T)]р dT = ∫ cр dT
Т1 Т1
Для случая, когда теплоемкость ср в рассматриваемом интервале температур не зависит от температуры и, следовательно, может быть вынесена за знак интеграла, получаем:
s2 (v, Т2) - s1 (v, Т1) = cр ℓn(Т2 /T1),
т. е. температурная зависимость энтропии на изобаре имеет логарифмический характер. Вполне понятно сходство этого уравнения с уравнением для разности энтропий на изохоре; различие состоит лишь в множителе перед In (Т2/Т1): в одном случае это изохорная теплоемкость cv, в другом — изобарная теплоемкость ср.
Слайд 39ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС
Изотермический процесс, характеризующийся постоянством температуры тела во время процесса
(Т
= const).
Если известны параметры одного состояния, то параметры другого, лежащего на той же изотерме, определяются, если известен еще какой-либо его параметр.
Для идеального газа давления и объемы в любых точках на изотерме связаны уравнением Бойля-Мариотта:
р1 v1 = р2 v2
т.е. зависимость объема от давления на изотерме для идеального газа имеет характер гиперболы.
Изотермы реального газа, жидкостей и твердых тел имеют более сложный характер.
Если известны параметры одного состояния, то параметры другого, лежащего на той же изотерме, определяются, если известен еще какой-либо его параметр.
Для идеального газа давления и объемы в любых точках на изотерме связаны уравнением Бойля-Мариотта:
р1 v1 = р2 v2
т.е. зависимость объема от давления на изотерме для идеального газа имеет характер гиперболы.
Изотермы реального газа, жидкостей и твердых тел имеют более сложный характер.
Слайд 40Важно подчеркнуть, что у любых веществ величина (dv/dp)T не может быть
положительной и, следовательно, всюду на изотерме с ростом давления удельный объем уменьшается.
Работа расширения системы в изотермическом процессе между точками изотермы 1 и 2 определяется с помощью общего соотношения
2
l1-2 = ∫ р dv
1
Для вычисления этого интеграла необходимо знать зависимость давления на изотерме от удельного объёма либо из уравнения состояния, либо непосредственно из эксперимента.
Для идеального газа уравнение работы расширения запишется как
l1-2 = RT ℓn(v2 / v1)
Слайд 41Как следует из приведенного уравнения, работа системы в изотермическом процессе равна
убыли свободной энергии системы.
Таким образом, располагая значениями свободной энергии в начале и в конце процесса, можно вычислить значение l1-2 .
Количество теплоты, подводимой к системе (или отдаваемой системой) в изотермическом процессе, определяется из известного соотношения dq=Tds так как Т=const, то l1-2 = Т(s2 - s1)
здесь s2 и s1 - энтропия в состояниях 2 и 1.
В случае идеального газа, для которого dи=сv dT, уравнение первого закона термодинамики можно записать в следующем виде: dq = сv dT + pdv,
т.е. количество работы, совершаемой идеальным газом в изотермическом процессе, равно количеству теплоты, подведённой к этому газу
q1-2 = l1-2 = RT ℓn(v2 / v1)
Слайд 42Изменение энтропии в изотермическом процессе, т. е. разность энтропий, соответствующих состояниям
1 и 2, вычисляется по уравнению, полученного в процессе ряда преобразований.
v2
s2 (Т, v2) - s1 (Т, v1) = ∫ [(∂р /∂T)]v dv
v1
Для того чтобы вычислить интегралы, стоящие в правой части уравнения, нужно располагать для данного вещества значениями (dv/dT)p или (др/дТ)v на изотерме, которые могут быть вычислены либо с помощью уравнений состояния, либо путем численного или графического дифференцирования экспериментальных данных по р, v, Т-зависимости данного вещества.
В случае идеального газа интегралы в уравнении легко могут быть вычислены.
Слайд 43Для идеального газа
(dv/dT)p = (R / р); (др/дТ)v = (R / v).
Отсюда получаем
s2 (Т, р2) - s1 (Т, р1) = RT ℓn(р2 / р1)
s2 (Т, v2) - s1 (Т, v1) = RT ℓn(v2 / v1)
Определим теплоемкость изотермического процесса. Из определения теплоемкости следует, что для изотермического процесса, у которого подвод (или отвод) теплоты к системе не приводит к изменению температуры системы, будет равна бесконечно сТ = ± ∞.
(знак плюс соответствует подводу теплоты к системе, знак минус — отводу теплоты от системы).
Слайд 44АДИАБАТНЫЙ ПРОЦЕСС
Адиабатический процесс, когда тело помещено в теплоизолирующую оболочку, не допускающую
теплообмена между телом и окружающей средой.
Адиабатным процессом называют такой термодинамический процесс, в котором к системе не подводится и от системы не отводится теплота, т. е.
dq = 0.
Термодинамическую систему, в которой протекает адиабатный процесс, можно представить себе в виде некоторого объема, ограниченного оболочкой, снабженной идеальной теплоизоляцией, абсолютно не пропускающей теплоту; такую оболочку называют адиабатной.
Адиабатным процессом называют такой термодинамический процесс, в котором к системе не подводится и от системы не отводится теплота, т. е.
dq = 0.
Термодинамическую систему, в которой протекает адиабатный процесс, можно представить себе в виде некоторого объема, ограниченного оболочкой, снабженной идеальной теплоизоляцией, абсолютно не пропускающей теплоту; такую оболочку называют адиабатной.
Слайд 45В реальных условиях процесс является адиабатным в тех случаях, когда система
снабжена хорошей теплоизоляцией или когда процесс расширения (сжатия) газа происходит настолько быстро, что не успевает произойти сколько-нибудь заметный теплообмен газа с окружающей средой.
Поскольку для обратимого процесса в соответствии с уравнением dq=Tds, с учетом (dq = 0) получаем, что в обратимом адиабатном процессе ds = 0, т. е. энтропия системы сохраняется постоянной. Иными словами, обратимый адиабатный процесс является в то же время изоэнтропным процессом.
Мы не случайно подчеркиваем здесь, что речь идет об обратимом адиабатном процессе, так как адиабатный процесс может быть и необратимым. Например, течение реального газа в шероховатой трубе, снабженной идеальной теплоизоляцией, исключающей процесс теплообмена через стенки трубы.
Слайд 46Течение газа в этом случае будет адиабатным, так как извне к
газу не подводится и от него не отводится теплота. Но поскольку течение реального газа в шероховатой трубе всегда сопровождается трением, приводящим к диссипации (рассеянию) энергии потока, этот процесс необратим: как и всякий необратимый адиабатный процесс, он идет с повышением энтропии системы. Для необратимых процессов имеет место неравенство Tds>dq.
В рассматриваемом случае необратимого адиабатного процесса dq=0, но ds>0. Следовательно, необратимый адиабатный процесс не является изоэнтропным.
Таким образом, можно сказать, что всякий изоэнтропный процесс в изолированной системе является адиабатным, но не всякий адиабатный процесс является изоэнтропным (изоэнтропными являются только обратимые адиабатные процессы).
Слайд 47Для определения связи между собой параметров различных состояний в обратимом адиабатном
процессе определим
дифференциальное уравнение изоэнтропного процесса.
Запишем объединенные уравнения первого и второго законов термодинамики
Tds = du + pdv; Tds = dh – vdp.
Для изоэнтропного процесса (ds=0) эти уравнения приобретают следующий вид:
du = - pdv; dh = vdp
отсюда
(∂u/∂v)s= - р; (∂h/∂p)s = v
С помощью этих соотношений нетрудно получить следующую зависимость:
(∂h/∂u)s = - (v/p) (∂p/∂v)s
Это и есть дифференциальное уравнение изоэнтропного процесса. Оно показывает, как связано изменение калорических свойств системы (h и и) с изменением ее
Слайд 48термических свойств (р и v) в изоэнтропном процессе. Введем следующее обозначение:
k = (∂h/∂u)s
Будем называть величину k показателем изоэнтропного процесса (или показателем изоэнтропы). С учетом введенного обозначения дифференциальное уравнение изоэнтропного процесса приобретает следующий вид:
- (v/p) (∂p/∂v)s = k
Произведение, стоящее в левой части уравнения , может быть преобразовано следующим образом:
dℓnp = -kℓnv
Это дифференциальное уравнение устанавливает связь между р и v в изоэнтропном процессе.
Интегрируя это соотношение между точками 1 и 2 на изоэнтропе, получаем:
v2
ℓn(p2 / p1) = - ∫ kdℓnv
v1
Слайд 49Если в рассматриваемом интервале изменения состояния системы (между точками 1 и
2) показатель изоэнтропы k остается неизменным, то k можно вынести за знак интеграла, и тогда можно получить:
ℓn(p2 / p1) = - k ℓn(v2 / v1)
или, что то же самое
ℓn(p2 / p1) = k ℓn(v1 / v2).
В свою очередь это соотношение может быть представлено в виде:
ℓn(p2 / p1) = ℓn(vk1 / vk2).
Потенциируя это равенство, получаем:
(p2 / p1) = (vk1 / vk2).
отсюда
p1 vk1 = p2 vk2
Аналогично, переводя систему по изоэнтропе в любое третье состояние с параметрами p3 и v3, можно показать, что
p1 vk1 = p2 vk2 = p3 vk3 = const.
Слайд 50Таким образом, для любого состояния системы в изоэнтропном процессе (при условии,
что показатель изоэнтропы k остается неизменным)
pvk = const.
Это соотношение носит название уравнения адиабаты Пуассона. Если показатель изоэнтропы k изменяется с изменением состояния системы и известен характер зависимости k на изоэнтропе, то для расчета величины р2 по известным р1 , v1 и v2 следует вычислить интеграл, стоящий в правой части, численными методами по известным значениям k.
Уравнения изоэнтропного процесса справедливы и для газа, и для жидкости, и для твердого тела.
Значение показателя изоэнтропы k (которое само по себе может быть использовано в качестве параметра состояния) оказывается существенно различным в различных фазовых состояниях вещества.
Слайд 51Для твердых тел и жидкостей k весьма велико, причем значение k
заметно изменяется с температурой. Так, для воды при t=0°С k=3602000, при t=50°С k=187000, при t=100°С k=22300. Для газов и паров значение k меняется с температурой (уменьшается) относительно слабо, причем для большинства газов значения k лежат в интервале
1,3—1,7; значения k заметно изменяются лишь вблизи пограничной кривой. Для воздуха показатель изоэнтропы в идеально-газовом состоянии равен примерно 1,40.
Работа расширения системы в любом изоэнтропном процессе определяется по формуле:
l1-2 = u1 – u2
это следует из уравнения dq = du + pdv (dq = 0).
Таким образом, в адиабатном (изоэнтропном) процессе работа расширения системы совершается за счёт убыли внутренней энергии системы.
Слайд 52Приведенное уравнение справедливо не только для изоэнтропного, т.е. обратимого адиабатного процесса,
но и не обратимого адиабатного процесса.
Для идеального газа уравнение для определения работы расширения, в зависимости от известных параметров, запишется как:
l1-2 = [R / (k-1)] (Т1 – Т2);
l1-2 = [p1 v1 / (k-1)];
l1-2 = [1 / (k-1)] (p1 v1 - p2 v2 ).
Так как для идеального газа внутренняя энергия зависит только от температуры и не зависит от объема, то в соответствии с уравнением du = сvdT имеем:
T1
u1(s1,T1) – u2 (s2,T2) = ∫ сvdT
T2
Слайд 53
T2
Отсюда l1-2 = ∫ сv dT.
T1
Если пренебречь зависимостью теплоемкости cv идеального газа от температуры или воспользоваться понятием средней в данном интервале температур теплоемкости cсрv, то уравнение может быть представлено в следующем виде:
l1-2 = сv (T1 - T2 )
Подчеркнем еще раз, что данное уравнение применимо и для реальных веществ, и для идеальных газов .
Изменение энтропии в изоэнтропном процессе также как и количество теплоты, подводимой к системе в изоэнтропном процессе, равно нулю.
Слайд 54ПОЛИТРОПНЫЕ ПРОЦЕССЫ
Политропными называют термодинамические процессы, удовлетворяющие уравнению
pvn = const
при произвольном, постоянном для данного политропного процесса значении п.
Величину п называют показателем политропы. Показатель политропы п для различных политропных процессов может принимать любые значения от +∞ до - ∞.
Кривую политропного процесса в диаграмме состояния называют политропой.
при произвольном, постоянном для данного политропного процесса значении п.
Величину п называют показателем политропы. Показатель политропы п для различных политропных процессов может принимать любые значения от +∞ до - ∞.
Кривую политропного процесса в диаграмме состояния называют политропой.
Слайд 55Понятие о политропных процессах было введено в термодинамике по аналогии с
понятием об адиабатных процессах. Уравнение политропного процесса по внешнему виду сходно с уравнением адиабаты; однако существенная разница между этими уравнениями состоит в том, что если показатель изоэнтропы (адиабаты) k является в общем случае величиной переменной, то уже само понятие политропного процесса основано на предположении о том, что показатель политропы п является постоянной величиной. В политропном процессе к системе может подводиться (или отводиться от нее) теплота.
Понятие о политропных процессах широко используется главным образом при изучении процессов сжатия и расширения в газовых двигателях; зачастую политропные процессы оказываются удобными для аппроксимации действительных газовых процессов в двигателях.
Слайд 56Реальные процессы сжатия в газовых двигателях и компрессорах часто не являются
ни адиабатными, ни изотермическими, а занимают промежуточное положение между этими двумя видами процессов. Поэтому, обычно встречаемые на практике значения показателя п политропного процесса лежат в интервале от 1 до k.
Для любых точек на политропе уравнение можно записать в виде:
p1 vn1 = p2 vn2
Если политропный процесс осуществляется в идеальном газе, то из выше приведенного уравнения и уравнения Клапейрона нетрудно получить:
T2 / T1 = (v1 /v2)(n-1); T2 / T1 = (р2 /р1)(n-1) /n
Эти уравнения устанавливают связь между р, v и Т в любых двух точках на политропе; первое уравнение справедливо и для реального, и для идеального газов, тогда как уравнения последнии — только для идеального газа.
Слайд 57Помимо уже отмеченной нами технической целесообразности введение понятия политропного процесса представляет
большую ценность и в методическом отношении. Понятие политропного процесса обобщает все остальные известные нам термодинамические процессы; нетрудно убедиться в том, что изохорный, изобарный, изотермический и адиабатный процессы представляют собой частные случаи политропных процессов.
В самом деле, из уравнения политропного процесса pvn = const очевидно, что политропный процесс с показателем п=0 представляет собой обычный изобарный процесс p = const
Из уравнения pvn = const, переписанного в виде p1/nv = const, очевидно, что политропный процесс с показателем п= ± ∞ - это изохорный процесс: v = const.
Уравнение политропы с показателем n=k превращается в уравнение адиабаты Пуассона pvk = const.
Наконец, уравнение политропы с показателем п=1 — это уравнение идеального газа pv = const.
Слайд 58Последнее уравнение справедливо только для изотермического процесса в идеальном газе; получить
из уравнения политропы уравнение изотермы реального газа нельзя. Конечно, процесс п=1 в реальном газе возможен, но этот процесс не является изотермическим.
На рисунке представлена р, v-диаграмма, в которой нанесены кривые различных политропных процессов.
Слайд 59Работа расширения системы в политропном процессе между точками 1 в 2
определяется с помощью уравнения
2
l1-2 = ∫ р dv
1
Так как для политропы в соответствии с pvn = const имеем
р = p1 vn1 / vn . Интегрируя выражение для l1-2 (при интегрировании учтем, что p1 vn1 постоянная величина), получаем для работы расширения в политропном процессе:
l1-2 = [(p1 v1) / (n-1) ]∙[1 – (v1 /v2) (n-1) ]
или, что тоже самое
l1-2 = [(p1 v1) / (n-1) ]∙[1 – (р2 /р1) (n-1)/n ]
Количество теплоты подводимое или отводимое в политропном процессе определяется исходя из уравнения
q2-1 = u2 – u1 + l1-2
Выполнив ряд математических преобразований получаем уравнение определения количество теплоты подводимое или отводимое в политропном процессе.
Слайд 60
T2 v2
q2-1 = ∫ сv dT + ∫ [Т(∂р/∂Т)v - р]∂v
T1 v1
Для расчетов с помощью этого уравнения нужно знать параметры обеих точек на политропе: Т1 и v1 , Т2 и v2.
Если мы имеем дело с политропным процессом в идеальном газе (следует заметить, что при расчете ряда политропных процессов в газовых двигателях и компрессорах идеально-газовое приближение оказывается вполне достаточным для технических расчетов), то уравнения для расчетов q2-1 могут быть приведены к более простому виду.
q2-1 = [(R/n-1) сv] (T1 - T2)
Поскольку в соответствии с уравнением Майера сР - cv=R, находим:
q2-1 = сv ∙ {[(ср / сv) – n] / (n-1)} ∙ (T1 - T2)
Слайд 61Для идеального газа отношение теплоемкости ср к cv представляет собой показатель
изоэнтропы идеального газа
kид=cр / cv. С учетом этого уравнения выражение получим преобразуется к виду
q2-1 = сv ∙ [(k – n) / (n-1)] ∙ (T1 - T2)
Это соотношение определяет количество теплоты, подводимой к идеальному газу (или отводимой от него) в политропном процессе.
Так как в соответствии с общим определением теплоемкости cx=dqx/dT, теплоемкость политропного процесса можно определить как сп = dqn / dT
отсюда
dqn = сп dT
тогда
2
q2-1 = ∫ сn dT
1
Слайд 62Если теплоемкость сп в рассматриваемом интервале параметров между точками 1 и
2 сохраняется постоянной, то получаем следующее уравнение для расчета количества теплоты, подводимой к системе в политропном процессе:
q2-1 = сn ∙ (T1 - T2)
Сравнивая полученные уравнения, можно сделать вывод о том, что фигурирующий в правой части комплекс
cv(k-n)/(n—1) представляет собой не что иное, как теплоемкость идеального газа в политропном процессе:
сn = сv ∙ [(k – n) / (n-1)]
Слайд 63ДРОССЕЛИРОВАНИЕ. ЭФФЕКТ ДЖОУЛЯ — ТОМСОНА
Из опыта известно, что если на пути
струи газа или жидкости, протекающей по трубе или какому-либо другому каналу, встречается препятствие, приводящее к внезапному резкому сужению поперечного сечения струи, а затем сечение струи увеличивается, то давление протекающего газа (жидкости) за препятствием всегда оказывается меньшим, чем перед ним. Такое препятствие называют местным сопротивлением.
Эффект падения давления струи рабочего тела в процессе протекания через сужения в канале называют дросселированием, или мятием.
Эффект падения давления струи рабочего тела в процессе протекания через сужения в канале называют дросселированием, или мятием.
Слайд 64С процессом дросселирования приходится часто сталкиваться на практике, например при движении
воды через неполностью открытый водопроводный кран или при движении воздуха через неполностью открытый воздушный шибер. В обоих случаях вследствие сопротивления дроссельного органа (крана или шибера) давление за ним уменьшается.
Физически падение давления за местным сопротивлением обусловлено диссипацией энергии потока, расходуемой на преодоление этого местного сопротивления.