перетворення
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Передаточна функція систем автоматики. Стуктурно-динамічні схеми систем автоматики та їх перетворення. (Лекція 2) презентация
Содержание
- 1. Передаточна функція систем автоматики. Стуктурно-динамічні схеми систем автоматики та їх перетворення. (Лекція 2)
- 2. Питання 1. Статичні та динамічні характеристики лінійних
- 3. Статична характеристика – залежність вихідного сигналу елементу
- 4. Статичні характеристики: Коефіцієнт передачі елементу являє собою
- 5. Статичні характеристики: Похибка елементу: абсолютна;
- 6. Динамічні характеристики: Передаточна функція. Часові характеристики:
- 7. Питання 2. Лінеаризація диференційних рівнянь.
- 8. Лінеаризація рівнянь елементів САУ Лінеаризацією називається заміна
- 9. ЗАДАЧА Лінеаризувати нелінійне диференційне рівняння
- 10. Алгоритм приведення лінеаризованого диференційного рівняння до стандартної
- 11. Питання 3. Передаточна функція
- 12. Пьер Симон Лаплас 23.03.1749 - 05.03.1827
- 13. Пряме перетворення Лапласа: Зворотне перетворення Лапласа: Основні
- 14. Передаточна функція: У загальному вигляді лінеаризоване рівняння елемента має вигляд:
- 15. Передаточною функцією автоматичного пристрою називається відношення зображень
- 16. Питання 4. Стуктурно-динамічні схеми систем автоматики та їх перетворення.
- 17. В системах автоматичного управління застосовуються наступні з’єднання елементів: послідовне; узгоджено-паралельне; зустрічно-паралельне.
- 18. Структурно-динамічна схема послідовного з’єднання Передаточна функція послідовного
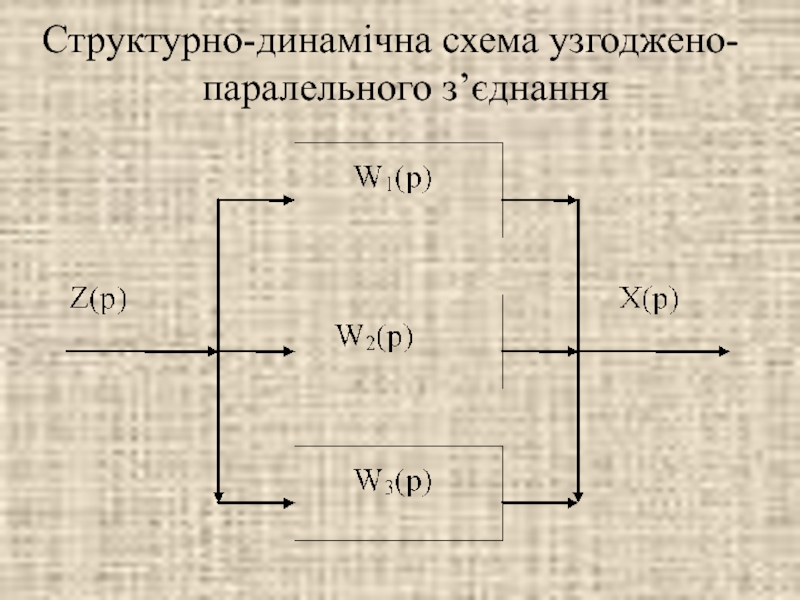
- 19. Структурно-динамічна схема узгоджено-паралельного з’єднання
- 20. Передаточна функція узгоджено-паралельного з’єднання ланок дорівнює алгебраїчній
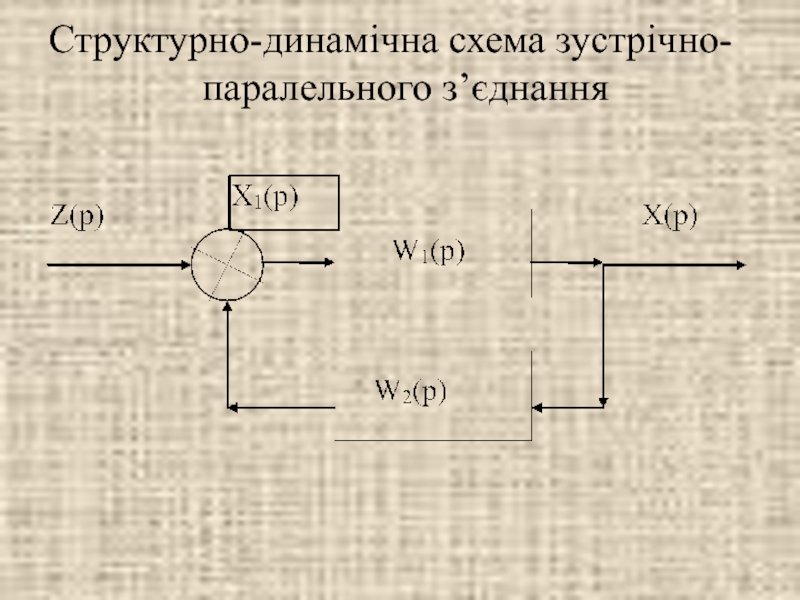
- 21. Структурно-динамічна схема зустрічно-паралельного з’єднання
- 22. Передаточна функція зустрічно-паралельного з’єднання ланок є дріб,
- 23. Завдання на самопідготовку: Абрамов Ю.А. “Основы пожарной автоматики“ стор. 94-102
Питання 1. Статичні та динамічні характеристики лінійних систем автоматики Можна виділити три типових
стани САУ: спокій або рівноважний стан; періодичні рухи; перехідний процес.
Слайд 1Лекція №2
Передаточна функція систем автоматики.
Стуктурно-динамічні схеми систем автоматики та їх
Слайд 2Питання 1. Статичні та динамічні характеристики лінійних систем автоматики
Можна виділити три
типових
стани САУ:
спокій або рівноважний стан;
періодичні рухи;
перехідний процес.
спокій або рівноважний стан;
періодичні рухи;
перехідний процес.
Слайд 3Статична характеристика – залежність вихідного сигналу елементу або системи від вхідного
в статичному режимі.
Статичний режим це такий режим, при якому всі сигнали, вхідні та вихідні, не змінюються у часі.
Ці характеристики визначаються або аналітично, або експериментально і представляються у вигляді: аналітичних залежностей, таблиць, графіків.
Слайд 4Статичні характеристики:
Коефіцієнт передачі елементу являє собою відношення вихідної величини елементу X
до вхідної величини Z або відношення диференціалів вихідної dx величини до диференціалу вхідної величини dz
Поріг чутливості – найменше значення вхідного сигналу, що здатне викликати зміну вихідного сигналу. Інтервал між порогами чутливості називається зоною нечутливості. Чим він більший тим елемент гірший.
Слайд 5Статичні характеристики:
Похибка елементу:
абсолютна;
відносна;
наведенна.
Похибка, яка виникає при
нормальних умовах експлуатації елементу (при яких він градуювався), називається основною.
При відхиленні умов експлуатації від нормальних до основної похибки додається похибка, яка називається додатковою.
Слайд 6Динамічні характеристики:
Передаточна функція.
Часові характеристики:
одинична перехідна функція;
імпульсна перехідна функція.
Частотні характеристики:
амплітудно-фазова ЧХ;
амплітудно-частотна;
фазово-частотна.
амплітудно-частотна;
фазово-частотна.
Диференційне рівняння
Слайд 8Лінеаризація рівнянь елементів САУ
Лінеаризацією називається заміна нелінійного диференційного рівняння (ДР) наближеним
до нього лінійним ДР.
Умови: а) заданий “опорний” (статичний) режим САУ. При цьому
z(t)= z0 =const; x(t)= x0 =const.
б) під час роботи САУ відхилення змінних від “опорних” значень невелике:
z(t)=z0+Δz(t) Δz(t) → 0
x(t)=x0+Δx(t) Δx(t) → 0
Умови: а) заданий “опорний” (статичний) режим САУ. При цьому
z(t)= z0 =const; x(t)= x0 =const.
б) під час роботи САУ відхилення змінних від “опорних” значень невелике:
z(t)=z0+Δz(t) Δz(t) → 0
x(t)=x0+Δx(t) Δx(t) → 0
Слайд 10Алгоритм приведення лінеаризованого диференційного рівняння до стандартної форми запису
Позбавляємось знаку Δ
перед змінними Δ x, Δ z.
В лівій частині рівняння записуємо вихідний сигнал та його похідні (х), в правій вхідний сигнал та його похідні (z).
Приводимо рівняння до такого вигляду, коли коефіцієнт при вихідному сигналі х дорівнює 1.
В лівій частині рівняння записуємо вихідний сигнал та його похідні (х), в правій вхідний сигнал та його похідні (z).
Приводимо рівняння до такого вигляду, коли коефіцієнт при вихідному сигналі х дорівнює 1.
Слайд 12Пьер Симон Лаплас
23.03.1749 - 05.03.1827
«То, что мы знаем, так ничтожно
по сравнению с тем, что мы не знаем»
астроном, физики математик.
Основные астрономические работы Лапласа относятся к области небесной механики.
Физические исследования Лапласа относятся к областям молекулярной физики, теплоты, акустики, оптики.
Лаплас — автор фундаментальных работ по математике и математической физике, прежде всего — трактата Аналитическая теория вероятностей
Слайд 13Пряме перетворення Лапласа:
Зворотне перетворення Лапласа:
Основні властивості перетворення Лапласа:
1. адитивність:
2. однорідність:
3. Правило
диференціювання:
Слайд 15Передаточною функцією автоматичного пристрою називається відношення зображень по Лапласу вихідного сигналу
до зображення по Лапласу вхідного сигналу при нульових початкових умовах
Слайд 17В системах автоматичного управління застосовуються наступні з’єднання елементів:
послідовне;
узгоджено-паралельне;
зустрічно-паралельне.
Слайд 18Структурно-динамічна схема послідовного з’єднання
Передаточна функція послідовного поєднання ланок дорівнює добутку передаточних
функцій ланок, які входять в це з'єднання:
Слайд 20Передаточна функція узгоджено-паралельного з’єднання ланок дорівнює алгебраїчній сумі передаточних функцій ланок,
які входять в це з'єднання:
Слайд 22Передаточна функція зустрічно-паралельного з’єднання ланок є дріб, в чисельнику якого записується
вираз для передаточної функції прямого ланцюга, а в знаменнику записується алгебраїчна сума одиниці та добутку передаточних функцій розімкнутого ланцюга.
