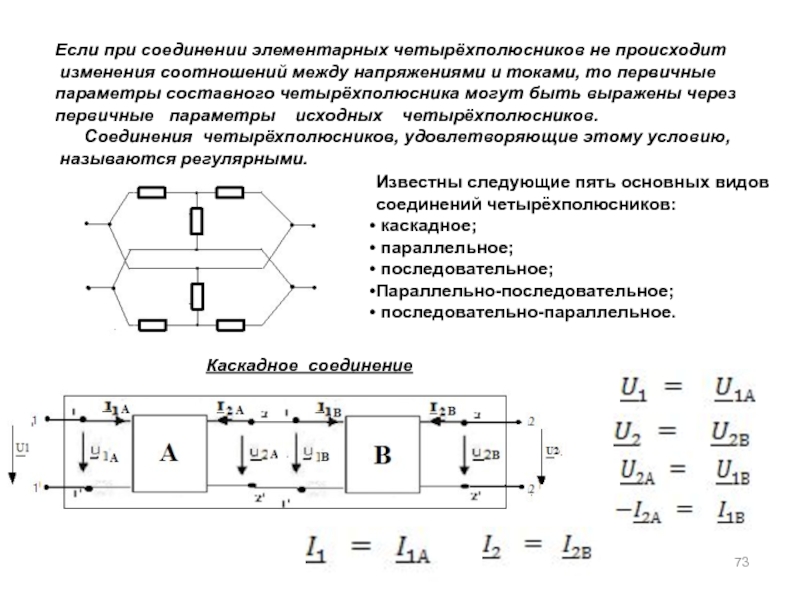
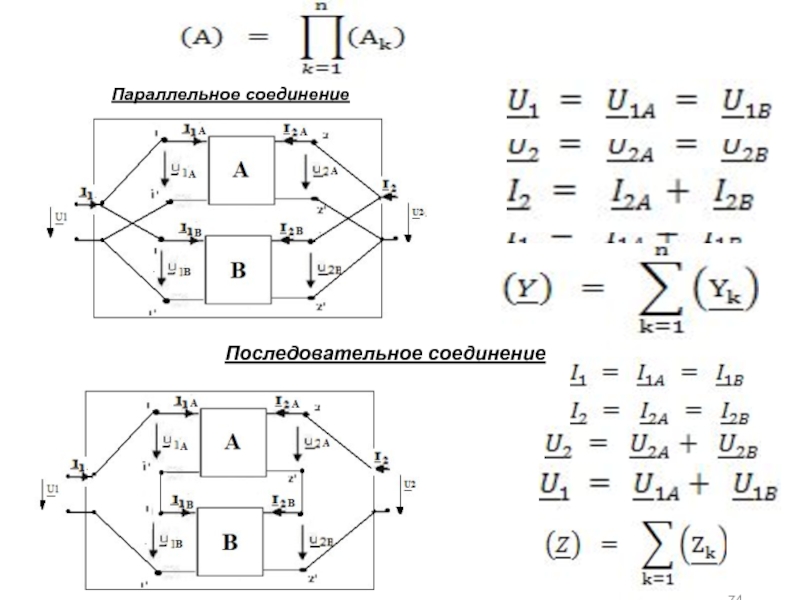
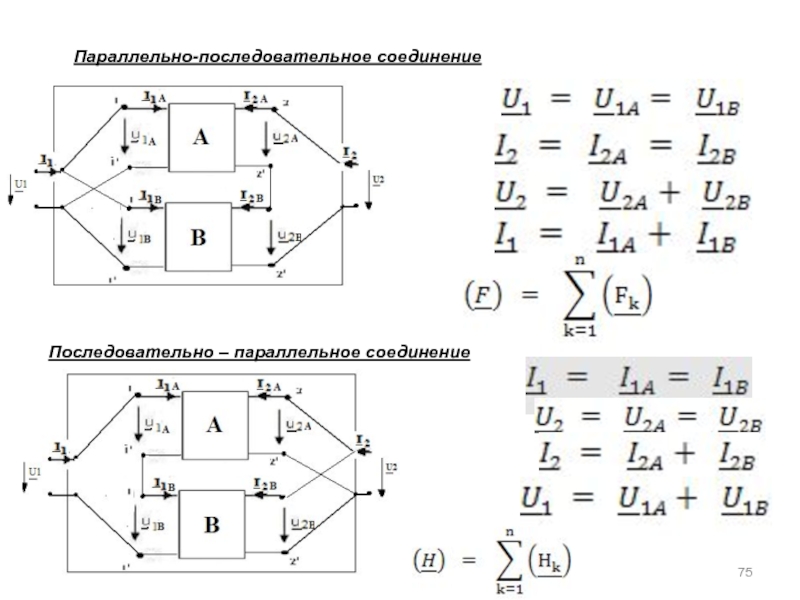
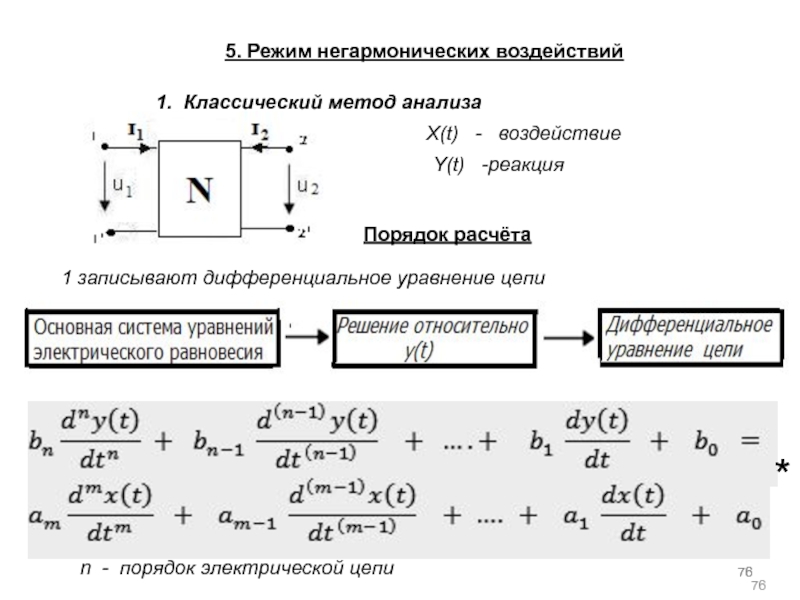
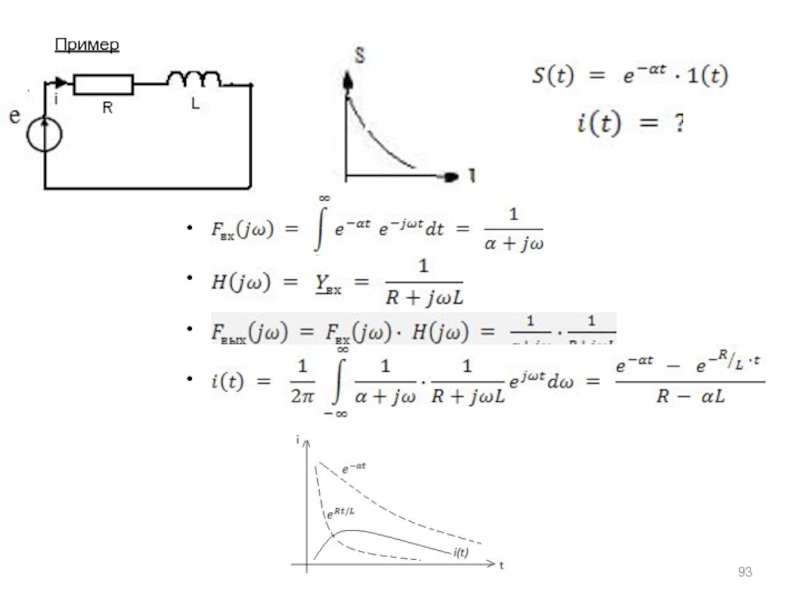
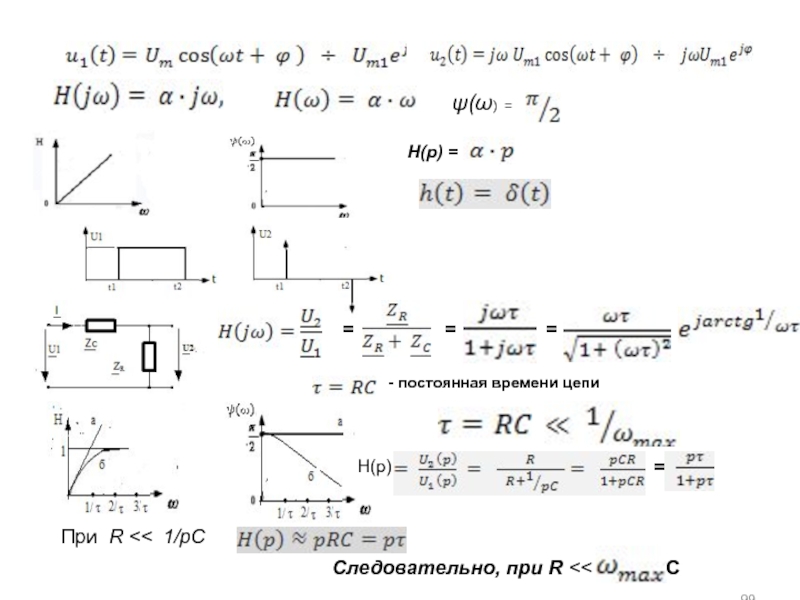
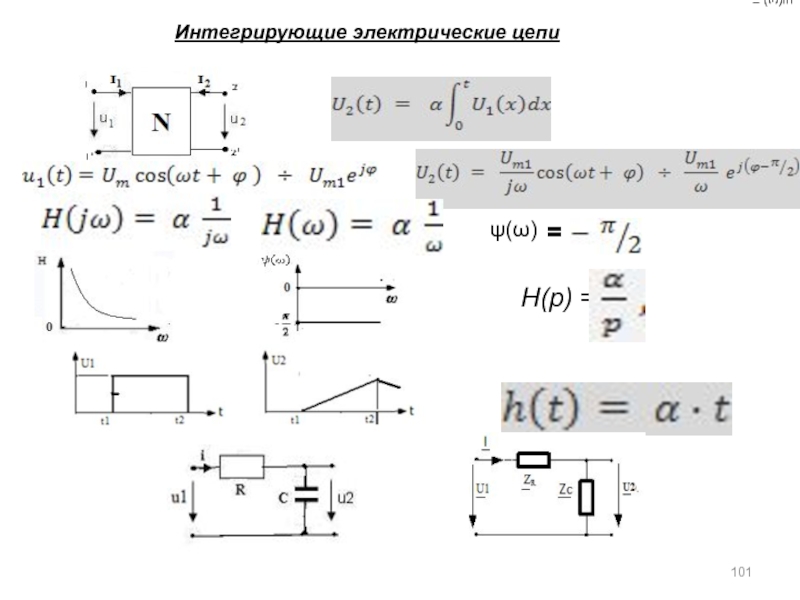
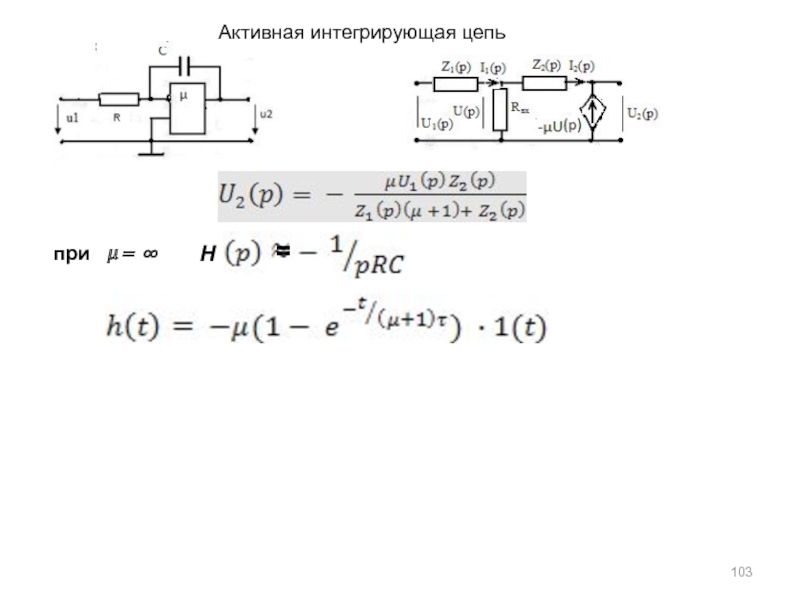
а) основная литература:
Попов В.П. Основы теории цепей. – М.: Высшая школа, 1985. –496 с.,
Попов В.П. Основы теории цепей. – М.: Высшая школа, 2013. –696 с.
Белецкий А.Ф. Теория линейных электрических цепей. – Санкт-Петербург: Лань, 2009. – 544 с.
Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под ред. В.П. Бакалова.- 2-е изд., перераб. и доп. - М.: Радио и связь, 2000. - 592 с.
Дмитриков В.Ф., Бакалов В.Ф., Крук Б.И. Основы теории цепей: Горячая линия- Телеком, 2009. – 596 с.
Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. –М: Высшая школа, 1986. –596 с.




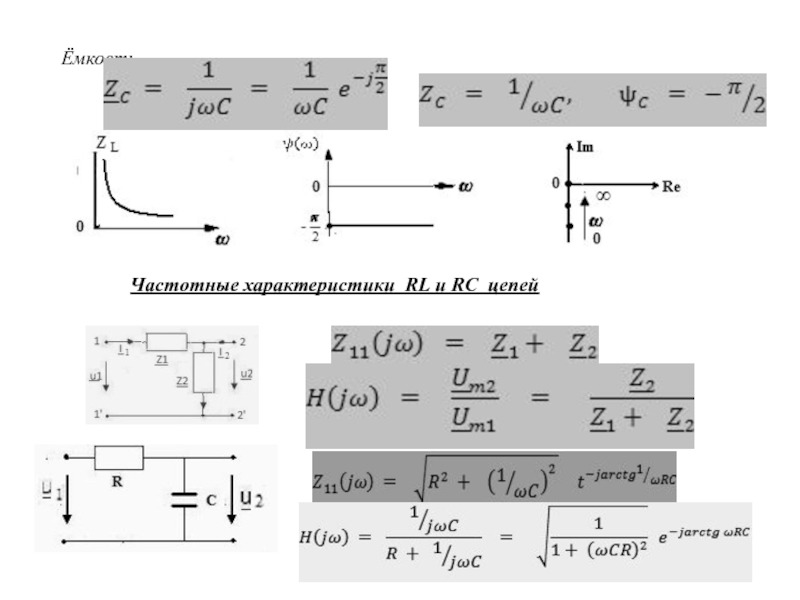
![ЁмкостьqC(t) = C uC(t)[ Ф ]iC = C duC / dt, . . wC =](/img/tmb/2/144157/fe74f45057f56415c8c6efe8f6065f69-800x.jpg)
![ИндуктивностьΨ(t) = L iL(t)uL = L diL/dt. . iL(t1) = .[ Гн ]uL(t) = Ψ(t)/](/img/tmb/2/144157/8dc8a38958c4fbf40065de90ea9fa21c-800x.jpg)