Вопросы, изложенные в лекции:
2.5 Цилиндрические и конические обечайки и замкнутые сферические оболочки
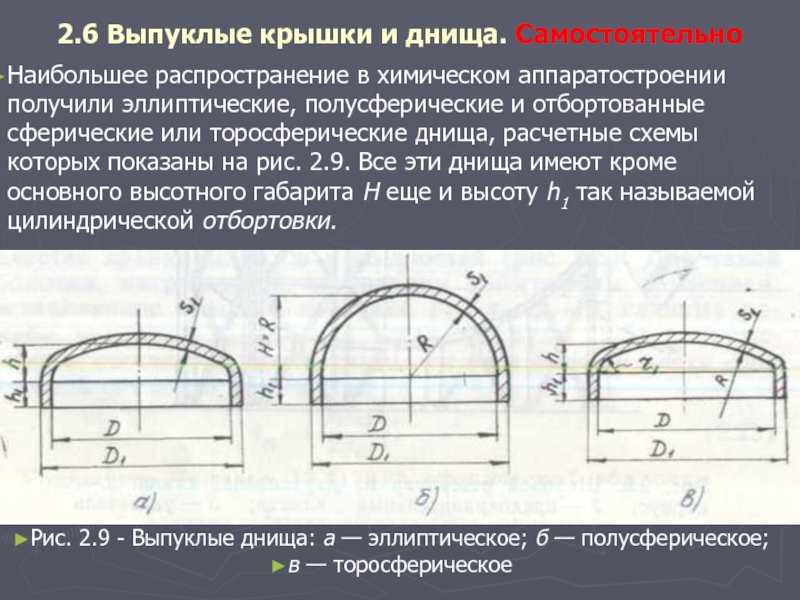
2.6 Выпуклые крышки и днища. Самстоятельно. Ист.1 с.28-31.
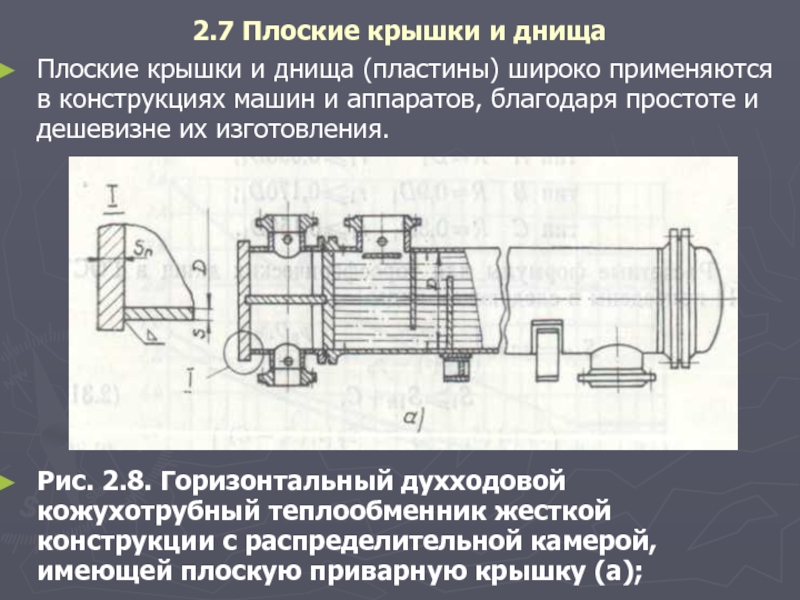
2.7 Плоские крышки и днища
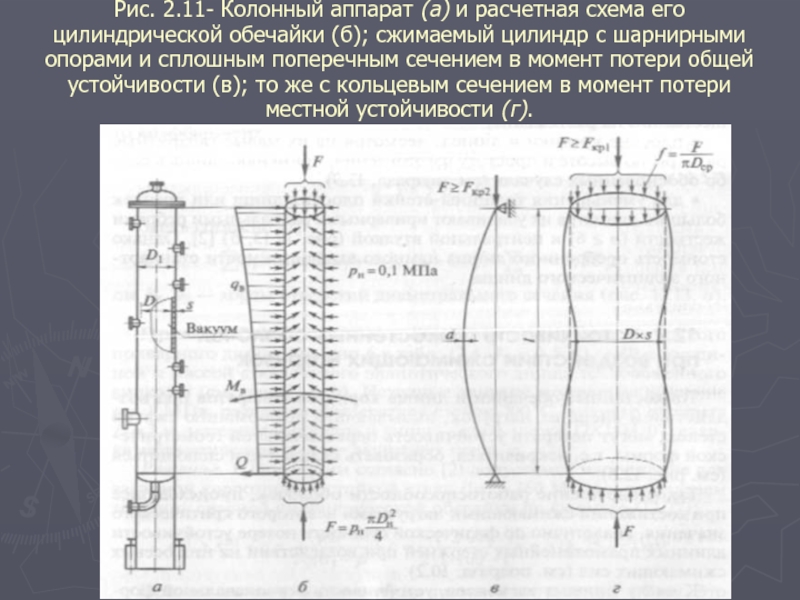
2.8 Устойчивость оболочек при воздействии сжимающих нагрузок
2.9 Гладкие конические обечайки и выпуклые днища Самостоятельно . Ист. 1, с. 49-52.
2.10 Узлы сопряжения оболочек. Самостоятельно . Ист. 2, с. 52-61.
Учебная литература:
Мильченко А.И. Особенности расчета типовых элементов химического оборудования. Корпуса аппаратов. Текст лекций, ЛТИ. – Ленинград, 1987, - 64с.
Мильченко А.И. Прикладная механика. Часть 2. Учебное пособие. – М: Изд. Центр Академия, 2013 – 256 с.



![Условие прочности по первой теории имеет вид σmax≤ [σ]. (2.8)Для нашего случая условие (2.8) запишем в](/img/tmb/5/438904/77fedbfa962414d2e442d04c10d267b7-800x.jpg)










![получимσmах= α·pp·(D/sl)2≤φ[σ]ОткудаВводя обозначения = kko, D = Dp и учитывая С, получим для проектного](/img/tmb/5/438904/9be8d1782db2a26d8c961ed92c9faeaa-800x.jpg)






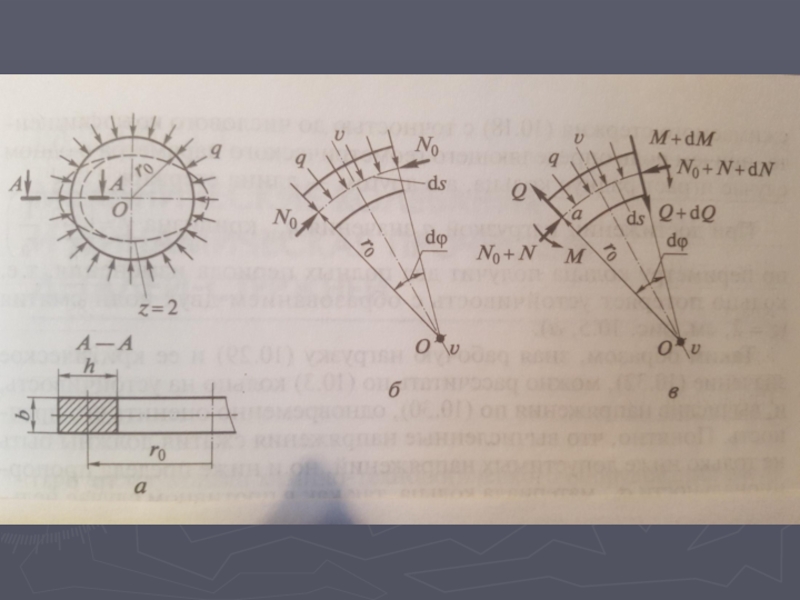
![При таком подходе допускаемое усилие [F] получается всегда ниже меньшего из двух допускаемых усилий [F]E](/img/tmb/5/438904/a3a6844d62c3ae735544b90502668c54-800x.jpg)






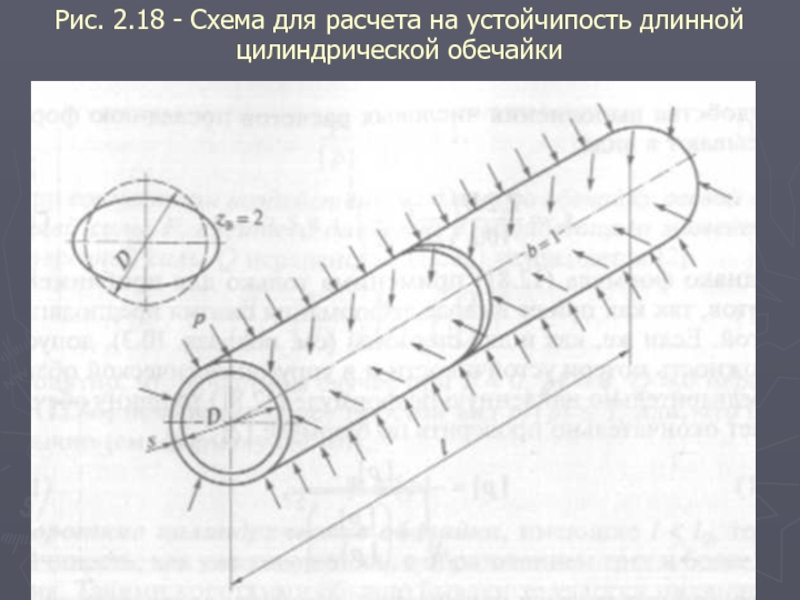



![Толщину же короткой обечайки для приближенных расчетов необходимо принять согласно ГОСТ [1] большей из следующих](/img/tmb/5/438904/589982070692f7514ea24016738c414f-800x.jpg)