ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные задачи динамики твердых тел. Уравнения Эйлера. Вращение вокруг неподвижной оси презентация
Содержание
- 1. Основные задачи динамики твердых тел. Уравнения Эйлера. Вращение вокруг неподвижной оси
- 2. 1. Основные задачи динамики твердого тела Дана
- 3. 2. Исходные ур-ия движение свободного твердого тела
- 4. 3. Сведение к задаче о враще-нии вокруг
- 5. 4. Вычисление момента количеств движения
- 6. 5. Уравнения вращения в непод-вижной системе координат
- 7. 6. Воспоминания из кинематики =
- 8. 7. Уравнения Эйлера Динамические уравнения Эйлера
- 9. 8. Вращение вокруг неподвижной оси Рассмотрим твердое
- 10. 9. Теорема об изменении количества движения 3)
- 11. 10. Теорема об изменении момента количеств движения
- 12. 11. Уравнения движения уравнения для определения поперечных
- 13. 12. Пример Равнобедренный прямоугольный треугольник вращается
- 14. 13. Условия совпадения динами-ческих и статических реакций
- 15. 14. Альтернативная форма ур-й для определения поперечных
- 16. 15. Альтернативная форма ур-й для определения поперечных
- 17. 16. Пример 1 Центр
- 18. 17. Пример 2: постановка задачи
- 19. 18. Пример 2: вычисление моментов инерции. Способ 1.
- 20. 19. Пример 2: вычисление моментов инерции. Способ 2.
- 21. 20. Пример 2: завершение
- 22. 21. Физический маятник Физическим маятником называется твердое
- 23. 22. Теорема Гюйгенса уравнение движения физического маятника
- 24. 23. Экспериментальное определение моментов инерции 3)Для нахождения
1. Основные задачи динамики твердого тела Дана система сил действующих на твердое тело. Требуется описать движение тела Будем различать три ситуации: Твердое тело свободно
Слайд 21. Основные задачи динамики твердого тела
Дана система сил действующих на твердое
тело. Требуется описать движение тела
Будем различать три ситуации:
Твердое тело свободно СВОБОДНОЕ ДВИЖЕНИЕ
Твердое тело закреплено в одной точке ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
Твердое тело закреплено в двух точках ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Совсемпросто
4) Твердое тело закреплено в 3-х, 4-х,… точках
Суперпросто
Слайд 32. Исходные ур-ия движение свободного твердого тела
Свободное твердое тело имеет шесть
степеней свободы
Например: координаты центра масс и углы Эйлера, определяющие ориентацию тела относительно центра масс
Для описания движения нужны шесть уравнений.
Первые три из них даются теоремой о движении центра масс
Вторые три – теоремой об изменении момента количеств движения
Они служат для нахождения положения центра масс
Эти уравнения будут служить для нахождения ориентации тела относительно центра масс
Слайд 43. Сведение к задаче о враще-нии вокруг неподвижной точки
Теорема об изменении
момента количеств движения дает те же уравнения как будто бы твердое тело вращалось вокруг неподвижной точки C
Слайд 65. Уравнения вращения в непод-вижной системе координат
НЕУДОБНЫ. Потому что не только
компоненты , но и тензора инерции изменяются со временем из-за того, что тело со временем изменяет свою ориентацию относительно неподвижных осей.
ИДЕЯ№1: Перейти в подвижную систему координат, жестко связанную с телом
ИДЕЯ№2: Направить оси (xyz) по главным осям тензора инерции для точки О
Слайд 87. Уравнения Эйлера
Динамические уравнения Эйлера
Кинематические уравнения Эйлера
ПОВТОРИТЬ!
Полная система уравнений вращения тела
вокруг неподвижной точки
+
Слайд 98. Вращение вокруг неподвижной оси
Рассмотрим твердое тело, имеющее 2 неподвижные точки
О, О1
неподвижная система координат
подвижная система координат, жестко связанная с телом
реакции связей в О, О1
главный вектор и главный момент внешних сил
1) теоремы об изменении количества движения и момента количества движения (в неподвижной системе координат)
2) переход в подвижную систему координат
воспользовались известным из кинематики фактом:
абсолютная производная
относительная производная
(1)
(2)
Слайд 109. Теорема об изменении количества движения
3) вычисляем фигурирующие в (1) вектора
в подвижной СК
Слайд 1110. Теорема об изменении момента количеств движения
4) вычисляем фигурирующие в (2)
вектора в подвижной СК
Слайд 1211. Уравнения движения
уравнения для определения поперечных реакций
диф. ур-ие вращения Т.Т вокруг
оси
уравнение для определения
Слайд 1312. Пример
Равнобедренный прямоугольный треугольник вращается вокруг вертикальной оси, к которой он
подвешен своим катетом. Найти боковые давления на опоры. Треугольник считать тонкой однородной пластинкой.
Слайд 1413. Условия совпадения динами-ческих и статических реакций
уравнения для определения динамических поперечных
реакций
уравнения для определения статических поперечных реакций
При каких условиях динамические поперечные реакции совпадают со статическими?
ур-ия для
ур-ия для
определитель обеих систем
Динамические реакции при вращении твердого тела равны статическим
Ось вращения является главной центральной осью инерции тела.
Слайд 1514. Альтернативная форма ур-й для определения поперечных реакций
Исходные уравнения для
определения динамических поперечных реакций
(1)
(2)
(3)
(4)
(1a)
(2a)
(2a)
Слайд 1615. Альтернативная форма ур-й для определения поперечных реакций
(1a)
(2a)
(3a)
(4a)
Окончательный вид уравнений
для определения поперечных реакций в системе координат
Уравнения для определения дополнительных поперечных реакций
(1a)
(2a)
(3a)
(4a)
Слайд 1716. Пример 1
Центр тяжести махового колеса, вес которого Р = 300
кГ, находится на расстоянии 1 мм от горизонтальной оси вала; расстояния подшипников от колеса равны между собой. Найти реакции подшипников, если вал вращается равномерно, делая n=1200 об/мин. Маховик имеет
плоскость симметрии, перпендикулярную к оси вращения.
плоскость симметрии, перпендикулярную к оси вращения.
Статические реакции
Дополнительные реакции
Слайд 1817. Пример 2: постановка задачи
Вычислить добавочные динамические реакции в подшипниках А
и В при вращении вокруг оси АВ однородного тонкого кругового диска CD, предполагая, что ось АВ проходит через центр диска,
но вследствие неправильного рассвер-ливания втулка составляет с перпенди-
куляром к плоскости диска
но вследствие неправильного рассвер-ливания втулка составляет с перпенди-
куляром к плоскости диска
Дано: масса диска m = 3,27 кГ, радиус его r = 20 см, число оборотов n = 30 000 об/мин, расстояния AO = 50 см, ОВ = 30 см.
Статические реакции
Слайд 2221. Физический маятник
Физическим маятником называется твердое тело, вращающееся вокруг неподвижной оси
под действием силы тяжести.
Рассмотрим случай, когда ось вращения горизонтальна. Проведем через центр тяжести С тела плоскость, перпендикулярную к оси вращения. Точка пересечения О этой плоскости с осью вращения называется точкой подвеса.
диф. ур-ие вращения тела вокруг оси z
уравнение движения физического маятника
Случай малых колебаний
Период колебаний
Слайд 2322. Теорема Гюйгенса
уравнение движения физического маятника
уравнение движения математического маятника
Математический маятник с
длиной будет двигаться как физический
Приведенная длина физического маятника
Центр качания
=
Свойство взаимности (теорема Гюйгенса): Если старый центр качания сделать новой точкой подвеса, то старая точка подвеса станет новым центром качания
Д-во:
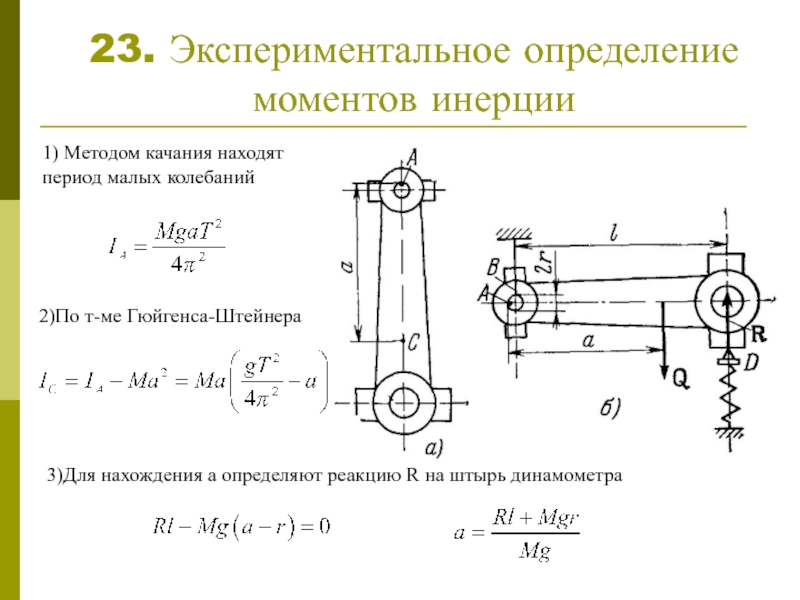
Слайд 2423. Экспериментальное определение моментов инерции
3)Для нахождения а определяют реакцию R на
штырь динамометра
1) Методом качания находят период малых колебаний
2)По т-ме Гюйгенса-Штейнера
