- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптика. Геометрическая оптика презентация
Содержание
- 1. Оптика. Геометрическая оптика
- 2. РАЗДЕЛ ОПТИКИ, В КОТОРОМ ИЗУЧАЮТСЯ ЗАКОНЫ РАСПРОСТРАНЕНИЯ
- 3. Основные понятия геометрической оптики Точечный источник света
- 4. Законы геометрической оптики Закон прямолинейного распространения света
- 5. Явление полного отражения Полное отражение света
- 6. Принцип Ферма В основу геометрической оптики
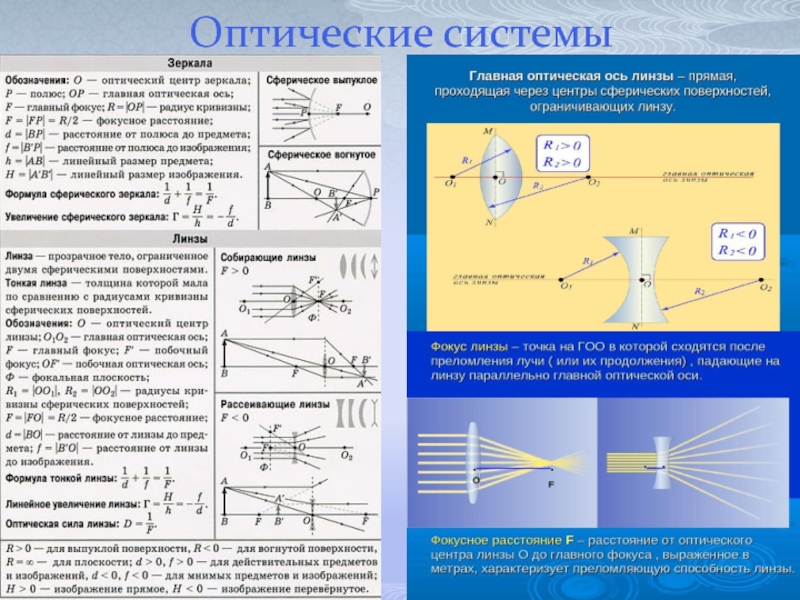
- 7. Оптические системы
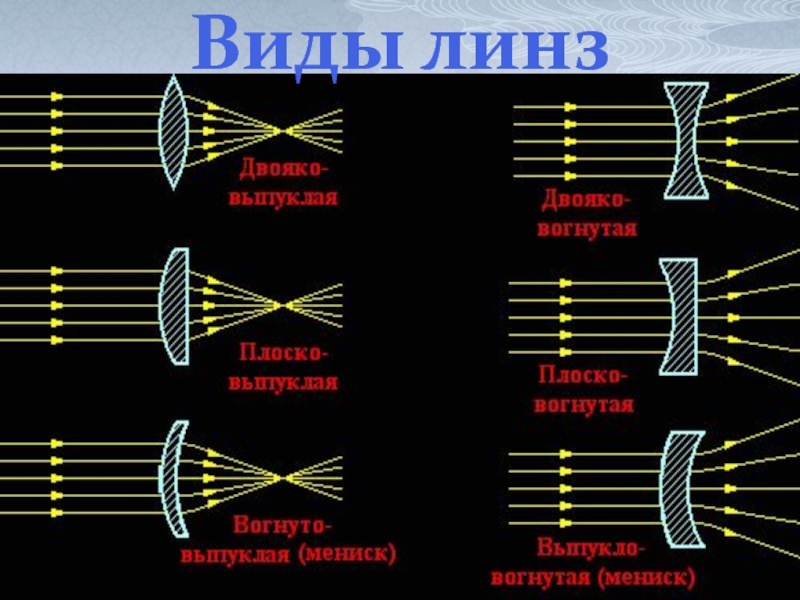
- 8. Виды линз
- 9. ДЛЯ ПОСТРОЕНИЯ ИЗОБРАЖЕНИЙ В ТОНКИХ ЛИНЗАХ ИСПОЛЬЗУЮТСЯ СЛЕДУЮЩИЕ ЛУЧИ: Три «замечательных» луча
- 10. Построение изображений в собирающей линзе Предмет находится
- 11. Предмет находится между фокусом и двойным фокусом
- 12. Предмет находится за двойным фокусом 1)
- 13. Построение изображений в рассеивающей линзе 1)
- 14. Построение изображений в зеркалах Плоские зеркала Изображение в плоском зеркале - мнимое Сферические зеркала
- 15. Аберрации оптических систем – искажение изображения в
- 16. Абберации Кома. Если через оптическую систему проходит
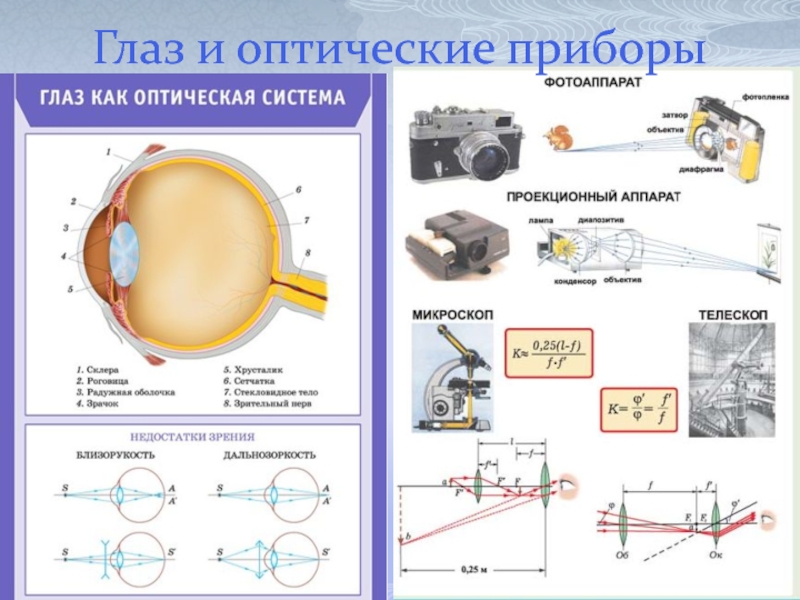
- 17. Глаз и оптические приборы
- 18. Фотометрические величины и единицы их измерения Яркость
- 19. Принцип Гюйгенса Христиан Гюйгенс
- 20. Интерференция света
- 21. Интерференция световых волн Интерференция света (от лат.
- 22. Пусть две волны одинаковой частоты, накладываясь
- 23. Условие интерференционных максимума и минимума Когерентные
- 24. Опыт Юнга (1802 г.) Положение точки
- 25. Расстояние между интерференционными полосами – расстояние между
- 26. Способы наблюдения интерференции
- 27. Зеркала Френеля Огюстен Жан Френель (1788
- 28. Бипризма Френеля Изготовленные из одного куска
- 29. Интерференция света при отражении от тонких пленок
- 30. Кольца Ньютона При отражении от
- 31. Применение интерференции Просветление оптики В основе просветления
- 32. ДИФРАКЦИЕЙ НАЗЫВАЕТСЯ СОВОКУПНОСТЬ ЯВЛЕНИЙ, НАБЛЮДАЕМЫХ ПРИ РАСПРОСТРАНЕНИИ
- 33. Принцип Гюйгенса - Френеля Для определения
- 34. Дифракция Френеля
- 35. Зоны Френеля Френель показал, что нахождение амплитуд
- 36. Площадь зон Френеля Площадь сферического сегмента
- 37. Дифракция от круглого отверстия
- 38. Дифракция от круглого диска
- 39. Дифракция от прямолинейного края полуплоскости Расположим полуплоскость
- 40. Зонная пластинка
- 41. ЙОЗЕФ ФРАУНГОФЕР (1787 – 1826 ГГ.)
- 42. Дифракция Фраунгофера на одной щели Плоская
- 43. Дифракционная решетка – система параллельных щелей равной
- 44. Дифракция на пространственной решетке. Формула Вульфа-Брэгга.
- 45. Поляризация света
- 46. Естественный и поляризованный свет
- 47. Степень поляризации Если пропустить частично поляризованный свет
- 49. Поляризация при отражении и преломлении. Закон Брюстера
- 50. Двойное лучепреломление – разделение упавшего на
- 51. Кристаллы, обладающие двойным лучепреломлением, подразделяются на одноосные
- 52. Двойное лучепреломление объясняется анизотропией кристаллов. В
- 53. Прохождение плоскополяризованного света через кристаллическую пластинку За
- 54. Взаимодействие ЭМВ с веществом
- 55. ЯВЛЕНИЯ, ОБУСЛОВЛЕННЫЕ ЗАВИСИМОСТЬЮ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ВЕЩЕСТВА ОТ
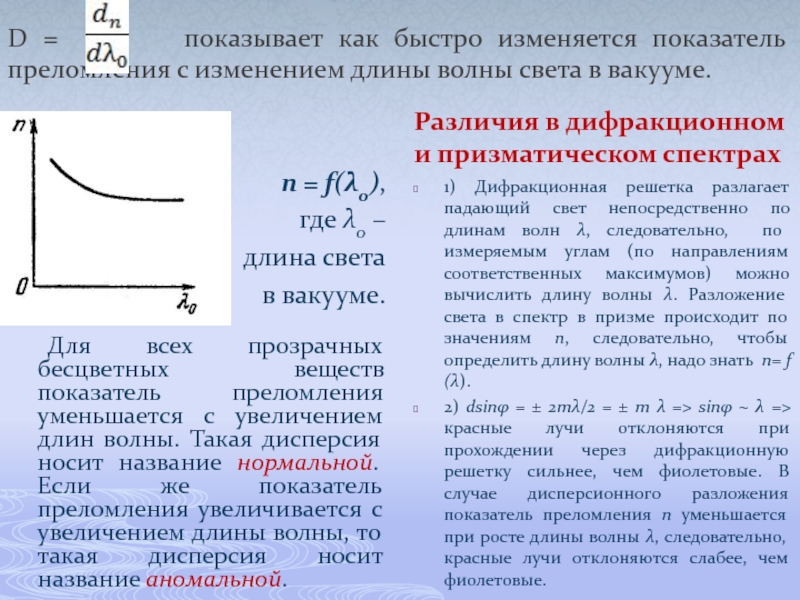
- 56. D = показывает как
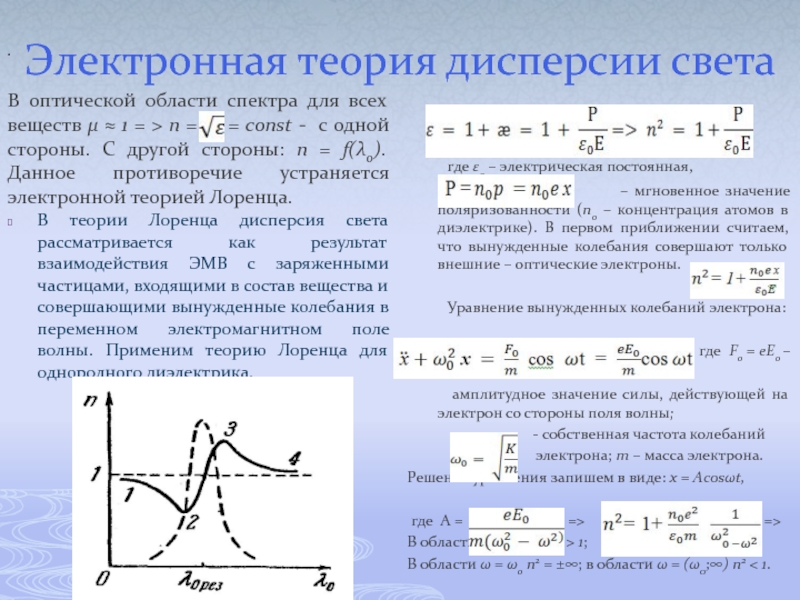
- 57. Электронная теория дисперсии света В оптической
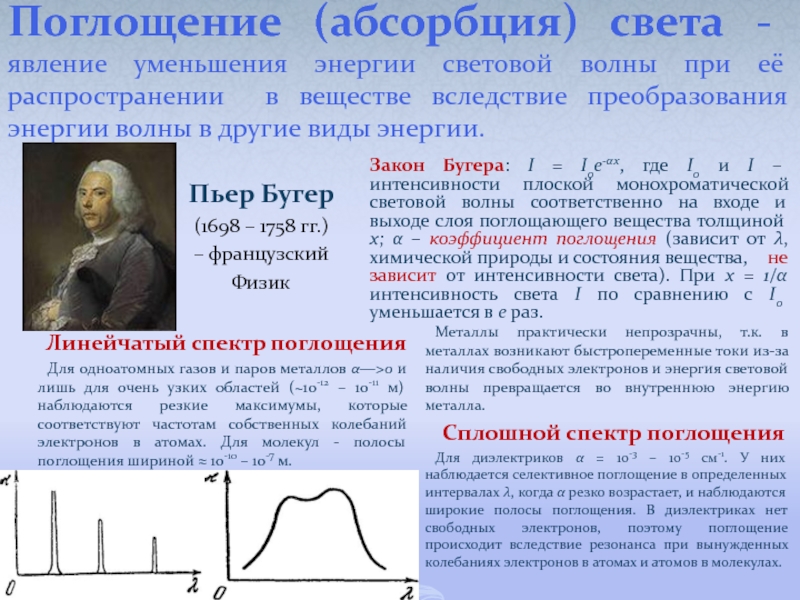
- 58. Поглощение (абсорбция) света - явление уменьшения энергии
- 59. Рассеяние света – дифракция на мелких
- 60. Эффект Вавилова-Черенкова (1934 г.) С.И. Вавилов (1892
Слайд 2РАЗДЕЛ ОПТИКИ, В КОТОРОМ ИЗУЧАЮТСЯ ЗАКОНЫ РАСПРОСТРАНЕНИЯ СВЕТА НА ОСНОВЕ ПРЕДСТАВЛЕНИЯ
Геометрическая оптика -
Слайд 3Основные понятия геометрической оптики
Точечный источник света – это источник света, размерами
Световой луч – нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии.
Границы применимости геометрической оптики:
Если наблюдение ведется на расстоянии, большем d2/?, где d – размер предмета, то начинают проявляться волновые свойства света.
Слайд 4Законы геометрической оптики
Закон прямолинейного распространения света
свет в оптически однородной среде распространяется
Закон отражения
Луч падающий, луч отраженный, а также перпендикуляр, восстановленный в точке падения луча на границе раздела двух сред, лежат в одной плоскости. Угол отражения равен углу падения.
Закон независимости световых пучков
Эффект, производимый пучком, не зависит от того, действуют ли одновременно пучки или они устранены.
Закон преломления
Луч падающий, луч преломленный, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.
n21 – относительный показатель преломления второй среды по отношению к первой.
n – абсолютный показатель преломления среды относительно вакуума.
Слайд 5Явление полного отражения
Полное отражение света наблюдается при распространении света из
Преломленный луч удаляется от нормали и угол преломления становится все больше пока преломленный луч не станет скользить по границе раздела двух сред, т.е. будет наблюдаться исчезновение преломленного луча.
Исчезновение (скольжение по границе раздела двух сред) преломленного луча наблюдается при некотором угле ?пр., называемом предельным углом. При углах падения ? > ?пр. падающий луч полностью отражается.
По мере приближения угла падения к предельному углу интенсивность преломленного луча уменьшается, а отраженного луча растет. При ? = ?пр. интенсивность преломленного луча стремится к нулю, а интенсивность отраженного луча становится равна интенсивности падающего луча. При углах падения ? = (?пр.; ?/2) луч полностью отражается в среду падения без преломления.
Слайд 6Принцип Ферма
В основу геометрической оптики может быть положен принцип, установленный французским
,
где υ - скорость света в данной точке среды =˃
dt = ( =˃ τ =
– время, затрачиваемое светом на прохождение пути от 1 до 2.
L = - оптическая длина пути;
L = nS – в однородной среде.
τ = =˃
принцип Ферма: свет распространяется по такому пути, оптическая длина которого минимальна. Из принципа Ферма =˃ обратимость световых лучей.
Слайд 9ДЛЯ ПОСТРОЕНИЯ ИЗОБРАЖЕНИЙ В ТОНКИХ ЛИНЗАХ ИСПОЛЬЗУЮТСЯ СЛЕДУЮЩИЕ ЛУЧИ:
Три «замечательных» луча
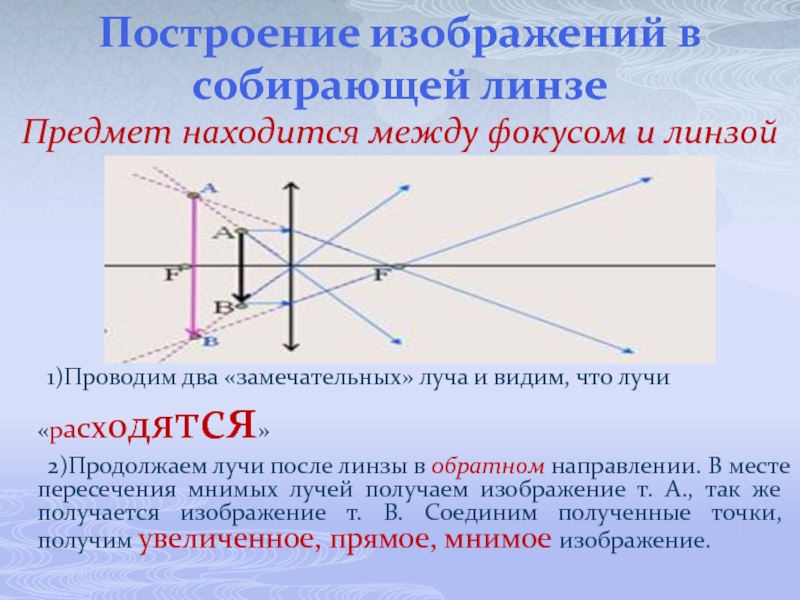
Слайд 10Построение изображений в собирающей линзе
Предмет находится между фокусом и линзой
1)Проводим два
2)Продолжаем лучи после линзы в обратном направлении. В месте пересечения мнимых лучей получаем изображение т. А., так же получается изображение т. В. Соединим полученные точки, получим увеличенное, прямое, мнимое изображение.
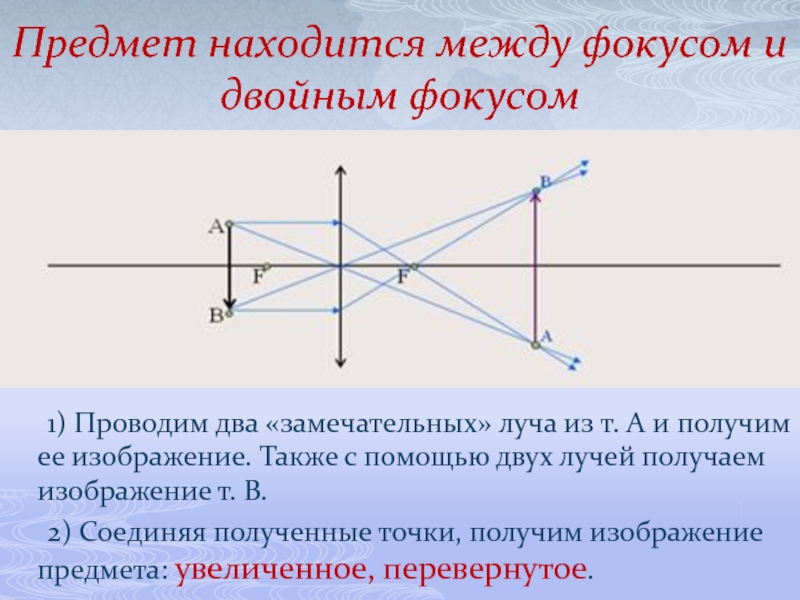
Слайд 11Предмет находится между фокусом и двойным фокусом
1) Проводим два «замечательных»
2) Соединяя полученные точки, получим изображение предмета: увеличенное, перевернутое.
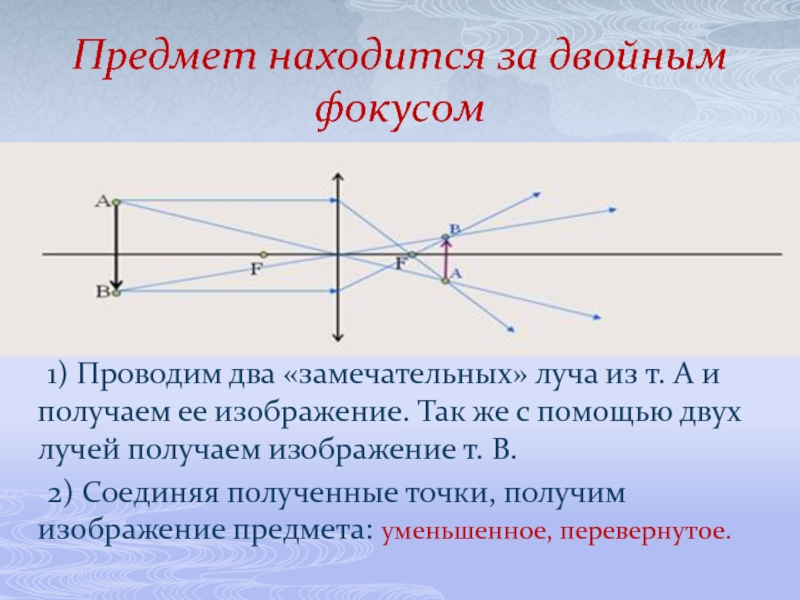
Слайд 12Предмет находится за двойным фокусом
1) Проводим два «замечательных» луча из т.
2) Соединяя полученные точки, получим изображение предмета: уменьшенное, перевернутое.
Слайд 13Построение изображений в рассеивающей линзе
1) Проводим луч из т. А через
2) Проводим луч из т. А параллельно оси, он преломится так, что его мнимое продолжение пройдет через фокус.
3) На пересечении двух лучей получаем изображение т. А. Аналогично получаем изображение т.В.
4) Соединяя полученные точки получаем изображение предмета: всегда мнимое, уменьшенное, прямое.
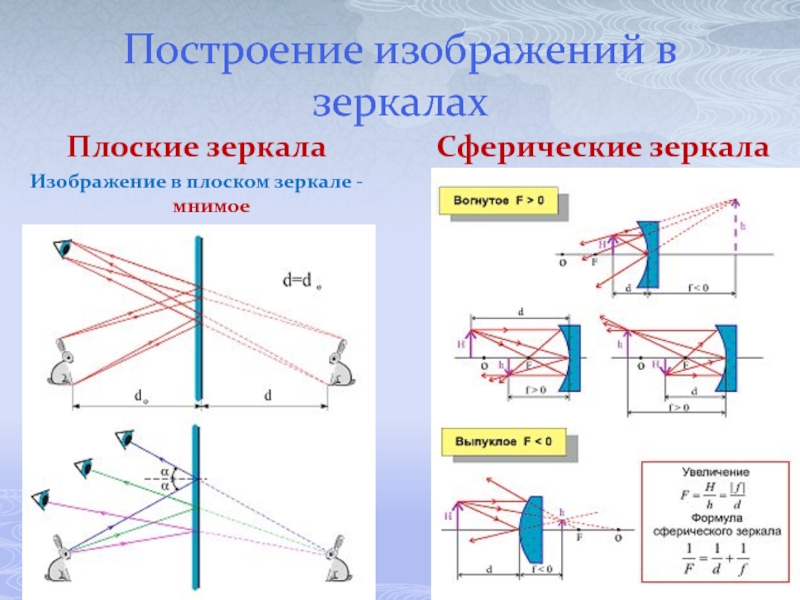
Слайд 14Построение изображений в зеркалах
Плоские зеркала
Изображение в плоском зеркале - мнимое
Сферические зеркала
Слайд 15Аберрации оптических систем – искажение изображения в оптических системах
Сферическая аберрация
Возникает
Слайд 16Абберации
Кома. Если через оптическую систему проходит широкий пучок от светящейся точки,
Дисторсия. При такой погрешности при больших углах падения лучей на линзу линейное увеличение для точек предмета, находящихся на разных расстояниях от главной оптической оси, несколько различается. Вследствие этого нарушается геометрическое подобие между предметами. Опасна в случаях проведения аэрофотосъемок, в микроскопии и т.д. Исправляют подбором составных частей оптической системы.
Астигматизм обусловлен неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на него светового пучка. Изображение точки, удаленной от главной оптической оси, наблюдается на экране в виде расплывчатого пятна эллиптической формы. Это пятно может вырождаться в прямую (вертикальную или горизонтальную) в зависимости от расстояния от экрана до оптического центра.
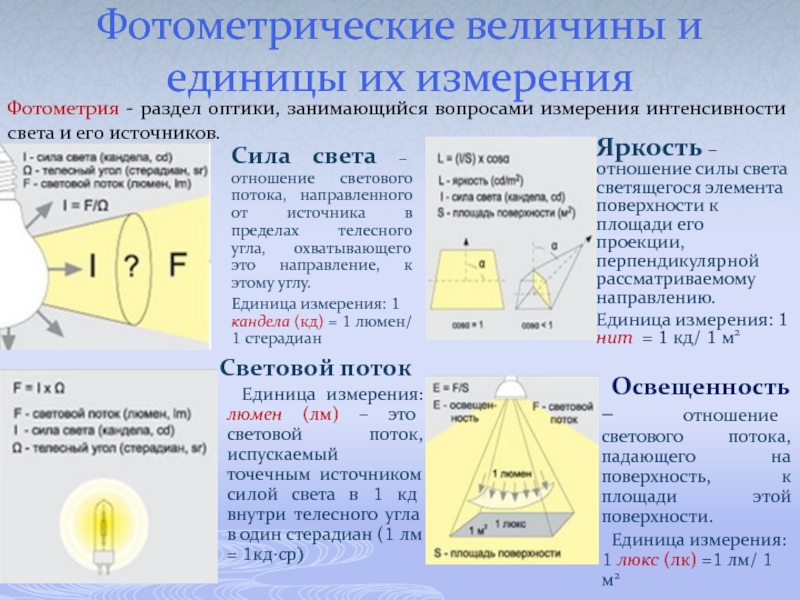
Слайд 18Фотометрические величины и единицы их измерения
Яркость – отношение силы света светящегося
Единица измерения: 1 нит = 1 кд/ 1 м2
Световой поток
Единица измерения: люмен (лм) – это световой поток, испускаемый точечным источником силой света в 1 кд внутри телесного угла в один стерадиан (1 лм = 1кд·ср)
Сила света – отношение светового потока, направленного от источника в пределах телесного угла, охватывающего это направление, к этому углу.
Единица измерения: 1 кандела (кд) = 1 люмен/ 1 стерадиан
Освещенность – отношение светового потока, падающего на поверхность, к площади этой поверхности.
Единица измерения: 1 люкс (лк) =1 лм/ 1 м2
Фотометрия - раздел оптики, занимающийся вопросами измерения интенсивности света и его источников.
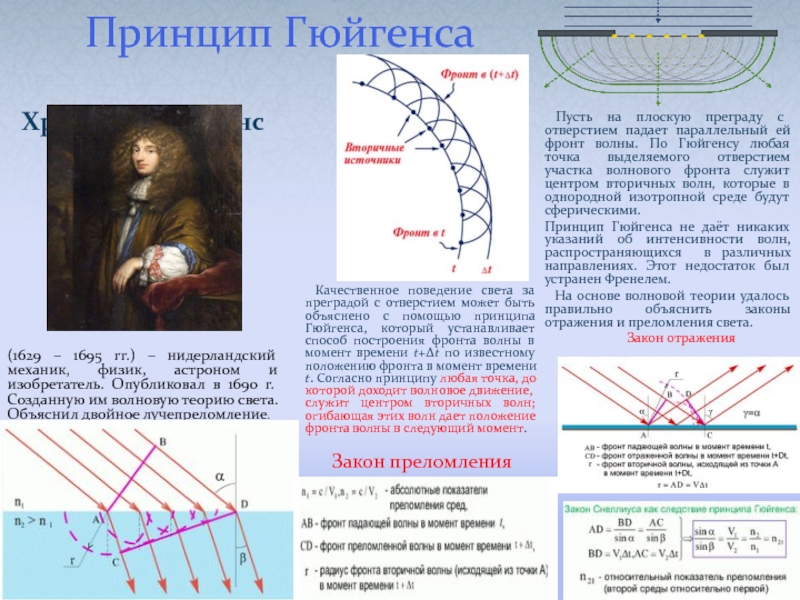
Слайд 19Принцип Гюйгенса
Христиан Гюйгенс
(1629 – 1695 гг.) – нидерландский механик, физик,
Качественное поведение света за преградой с отверстием может быть объяснено с помощью принципа Гюйгенса, который устанавливает способ построения фронта волны в момент времени t+Δt по известному положению фронта в момент времени t. Согласно принципу любая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент.
Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны. По Гюйгенсу любая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной изотропной среде будут сферическими.
Принцип Гюйгенса не даёт никаких указаний об интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем.
На основе волновой теории удалось правильно объяснить законы отражения и преломления света.
Закон отражения
Закон преломления
Слайд 21Интерференция световых волн
Интерференция света (от лат. inter – взаимно, между собой
Интерференция волн – одно из основных свойств волн любой природы. Интерференция света объясняет окраску тонких масляных пленок на поверхности воды, металлический отлив в окраске крыльев насекомых и птиц, голубоватый цвет просветленных линз оптических приборов.
Впервые интерференционные явления были исследованы И. Ньютоном, но он не смог их объяснить с точки зрения корпускулярной теории. Впервые интерференция была правильно объяснена с волновой точки зрения Т. Юнгом и О. Френелем. в начале XIXв.
Необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
Этому условию удовлетворяют монохроматические волны – волны определенной и строго постоянной частоты.
Волну можно приближенно считать монохроматической только в течение времени
, где ? ког. - время когерентности.
За промежуток времени ?ког. разность фаз колебаний изменится на ?.
Время когерентности – время, по истечении которого разность фаз волны в некоторой, но одной и той же точке пространства, изменяется на ?.
Слайд 22
Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в
х1 = А1cos (?t+?1); х2 = А2cos (?t+?2)
За меру интенсивности световой волны принимаем квадрат амплитуды световой волны: I = А2, тогда
Если разность фаз (?2 - ?1) = const, то колебания когерентны и
Если cos φ > 0, то I > I1+I2
Если cos φ < 0, то I < I1+I2
При наложении когерентных световых волн происходит перераспределение светового потока в пространстве, следовательно, в одних местах возникают максимумы, а в других минимумы интенсивности. Это явление носит название интерференции волн. Особенно отчетливо наблюдается при равной интенсивности интерферирующих волн: I1 = I2.
В максимумах: I = 4I1; в минимумах: I = 0 (для некогерентных волн везде: I = 2I1).
Некогерентность естественных источников света обусловлена тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью порядка 10-8 с и протяженностью около 3 м. Фаза нового цуга никак не связана с фазой предыдущего цуга. В испускаемой телом световой волне излучение одной группы атомов через время порядка 10-8 с сменяется излучением другой группы.
Слайд 23Условие интерференционных
максимума и минимума
Когерентные световые волны можно получить, разделив (с
Первая волна возбудит колебание:
Вторая волна возбудит колебание:
Разность фаз двух ввууувколебаний:
Оптическая разность хода:
? = n2s2 – n1s1 = L2 – L1, где L – оптическая длина пути; s – геометрическая длина пути; n – показатель преломления среды.
Если оптическая разность хода равна целому числу длин волн, то
? = ± m?0 (m = 0, 1, 2, …) – условие интерференционного максимума
Если оптическая разность хода равна полуцелому числу длин волн, то
? = ± (2m + 1)?0/2 (m = 0, 1, 2, …) – условие интерференционного минимума
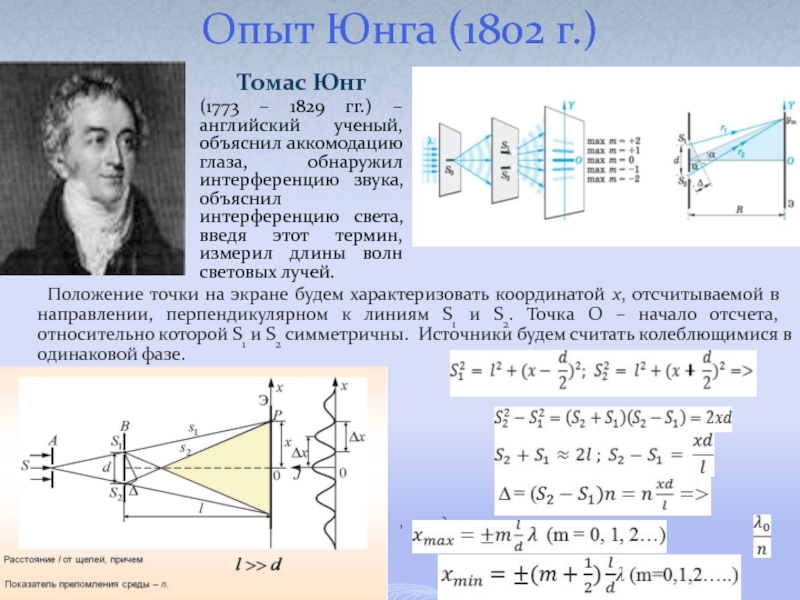
Слайд 24Опыт Юнга (1802 г.)
Положение точки на экране будем характеризовать координатой х,
, где λ =
Томас Юнг
(1773 – 1829 гг.) – английский ученый, объяснил аккомодацию глаза, обнаружил интерференцию звука, объяснил интерференцию света, введя этот термин, измерил длины волн световых лучей.
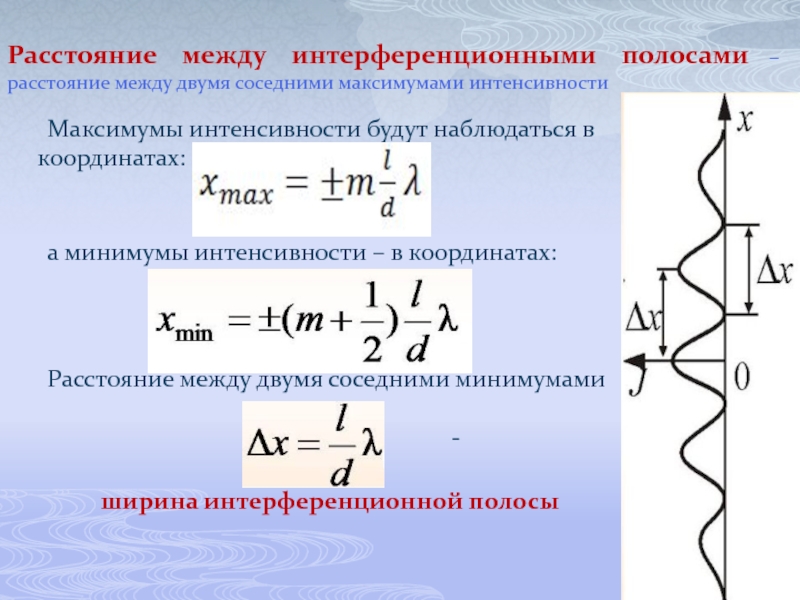
Слайд 25Расстояние между интерференционными полосами – расстояние между двумя соседними максимумами интенсивности
Максимумы
(m = 0, 1, 2, …)
а минимумы интенсивности – в координатах:
Расстояние между двумя соседними минимумами
-
ширина интерференционной полосы
Слайд 27Зеркала Френеля
Огюстен Жан Френель
(1788 – 1827 гг.) – французский физик,
Два плоских соприкасающихся зеркала OM и ON располагаются так, что их отражающие поверхности образуют угол, близкий к π (соответственно, угол φ- очень мал). Параллельно линии пересечения зеркал О на расстоянии r от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников S1 и S2.
Непрозрачный Э1 преграждает свету путь от источника S к экрану Э.
OQ- отражение луча SO от зеркала OM;
OP- отражение луча SO от зеркала ON;
Угол POQ = 2φ ; OS1= OS = r = OS2.
d = 2rsin φ ≈ 2rφ , так как φ ―>0;
а = rcosφ ≈ r =>
l = r + b, где b - расстояние от линии пересечения зеркал О до экрана Э.
Так как
∆х = ,
то ∆х = – ширина интерферен. полосы.
Область перекрытия волн имеет протяженность 2btgφ ≈ 2bφ.
Разделим эту длину на ширину полосы ∆х, найдём максимальное число интерференционных полос, которые можно наблюдать с помощью зеркал Френеля:
N =
Слайд 28Бипризма Френеля
Изготовленные из одного куска стекла две призмы с малым преломляющим
Если ζ ―> 0 и углы падения лучей на грань призмы не очень велики, то все лучи отклоняются призмой на практически одинаковый угол:
, где
n-показатель преломления призмы.
В результате образуются две когерентные цилиндрические волны, исходящие из мнимых S1 и S2, лежащих в одной плоскости с S.
d = 2asinφ≈2aφ = 2а(n-1) ζ – расстояние между источниками.
l = a+b – расстояние от источников до экрана.
Т.к. Δх = , то Δx = -
ширина интерференционной полосы.
2btgφ ≈ 2bφ = 2b(n-1) ζ – область перекрытия волн PQ.
N = -
максимальное число наблюдаемых полос.
Слайд 29Интерференция света при отражении от тонких пленок
b
При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световых волны, которые при известных условиях могут интерферировать.
Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных луча, один их которых отражается от верхней поверхности пластинки, второй – от нижней.
Δ = ns2 – s1 - разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в т. С, где s1 = BC, s2 = AO+OC.
Δ = 2 b tgϑ2sinϑ1 = 2b
Т.к. n sinϑ2 = sinϑ1 и
ncosϑ2 =
получим, что Δ = 2b
В т. С отражение происходит от границы раздела среды, оптически менее плотной, со средой, оптически более плотной. Следовательно, фаза волны претерпевает изменение на π.
В т. О отражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, так что скачка фазы не происходит (возникает φ= π).
Δ = 2b
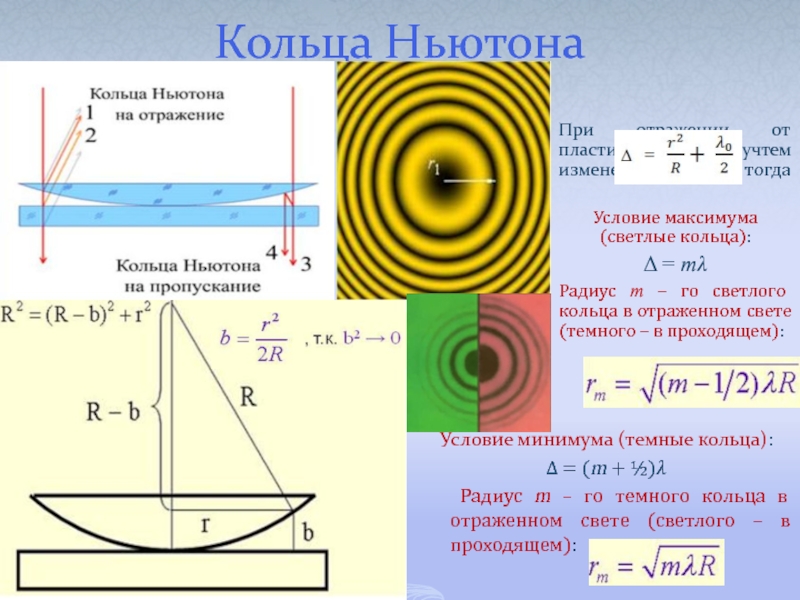
Слайд 30Кольца Ньютона
При отражении от пластинки учтем изменение фазы на ?, тогда
Условие
Δ = m?
Радиус m – го светлого кольца в отраженном свете (темного – в проходящем):
Условие минимума (темные кольца):
Δ = (m + ½)?
Радиус m – го темного кольца в отраженном свете (светлого – в проходящем):
Слайд 31Применение интерференции
Просветление оптики
В основе просветления оптики лежит интерференция при отражении от
Толщина пленки подбирается так, чтобы волны, отраженные от обеих поверхностей, гасили друг друга. Особенно хороший результат достигается в случае:
Одновременного гашения всех длин волн невозможно, то толщина пленки объектива подбирается так, чтобы гасились отраженные волны средней части спектра (зеленые):
Поэтому объективы с просветленной оптикой имеют характерный сиреневый оттенок.
Интерферометры –
приборы, позволяющие оценить качество обработки поверхности с точностью до 10-8 м по искривлению интерференционных полос.
Интерферометр Майкельсона (использован для проверки гипотезы о светоносном эфире)
Слайд 32 ДИФРАКЦИЕЙ НАЗЫВАЕТСЯ СОВОКУПНОСТЬ ЯВЛЕНИЙ, НАБЛЮДАЕМЫХ ПРИ РАСПРОСТРАНЕНИИ СВЕТА В СРЕДЕ С
Дифракция света
Слайд 33Принцип Гюйгенса - Френеля
Для определения колебания в т. Р, лежащей
Световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. В качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.
Слайд 35Зоны Френеля
Френель показал, что нахождение амплитуд результирующего колебания может быть осуществлено
Определим амплитуду светового колебания, возбуждаемого в точке Р сферической волной, распространяющейся в изотропной однородной среде из точечного источника.
Волновые поверхности такой волны симметричны относительно SP. Разобьем волновую поверхность на кольцевые зоны, построенные так, что расстояния от краёв любой зоны до точки Р отличаются на λ/2 – зоны Френеля.
Расстояние от внешнего края m -й зоны до точки Р:
,
где b - расстояние от вершины волновой поверхности О до точки Р.
Результирующие колебания, создаваемые любой из зон в целом, будут для соседних зон отличается по фазе на π.
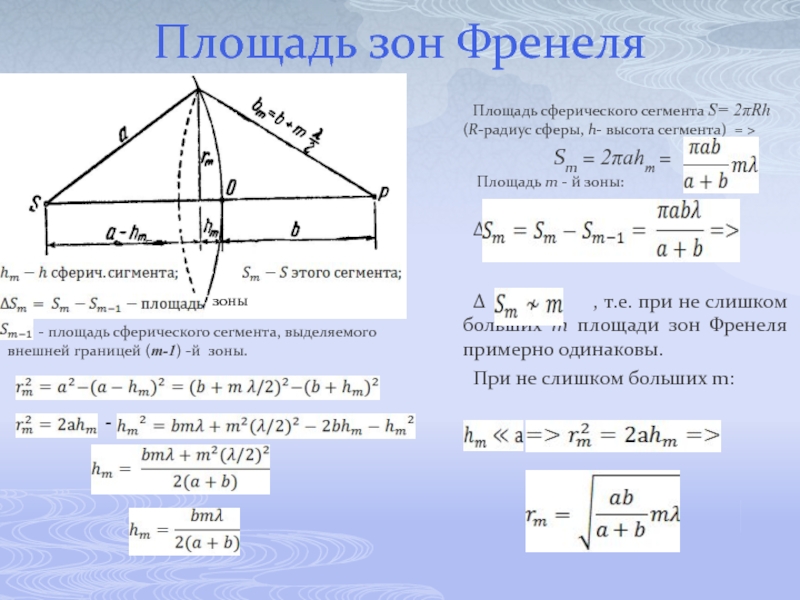
Слайд 36Площадь зон Френеля
Площадь сферического сегмента S= 2πRh (R-радиус сферы, h- высота
Sm = 2πahm =
Площадь m - й зоны:
Δ
Δ , т.е. при не слишком больших m площади зон Френеля примерно одинаковы.
При не слишком больших m:
зоны
- площадь сферического сегмента, выделяемого внешней границей (m-1) -й зоны.
-
Слайд 37Дифракция от круглого отверстия
Поставим на пути сферической световой волны непрозрачный Э
Фазы колебаний, возбуждаемых соседними зонами, отличаются на π, следовательно:
A = А1 – А2 + А3 – А4 +…±Аm
Берем знак «+», если m – нечетное,
знак «-» , если m- четное.
Представим:
Выражение в скобках равно 0. Тогда
) + (
Слайд 38Дифракция от круглого диска
Поместим между источником S и точкой Р
А = =
= -
А =
Освещенность может зависить только от расстояния r до точки Р. При небольшом числе закрытых зон => интенсивность в точке Р будет почти как в отсутствии преграды. Дифракционная картина имеет вид чередующийся светлых и темных концентрических колец. В центре картины помещается светлое пятно.
Если диск закрывает лишь небольшую часть центральной зоны, он не отбрасывает тень - освещенность как при отсутствии преград. Если диск закрывает много зон Френеля, чередование светлых и темных колец наблюдается только в узкой области на границе геометрической тени (Аm+1<< A1, светлое пятно отсутствует в центре и освещенность в области геометрической тени=0). Светлое пятнышко в центре тени, отбрасываемой диском, - пятно Пуассона (1818 г.)
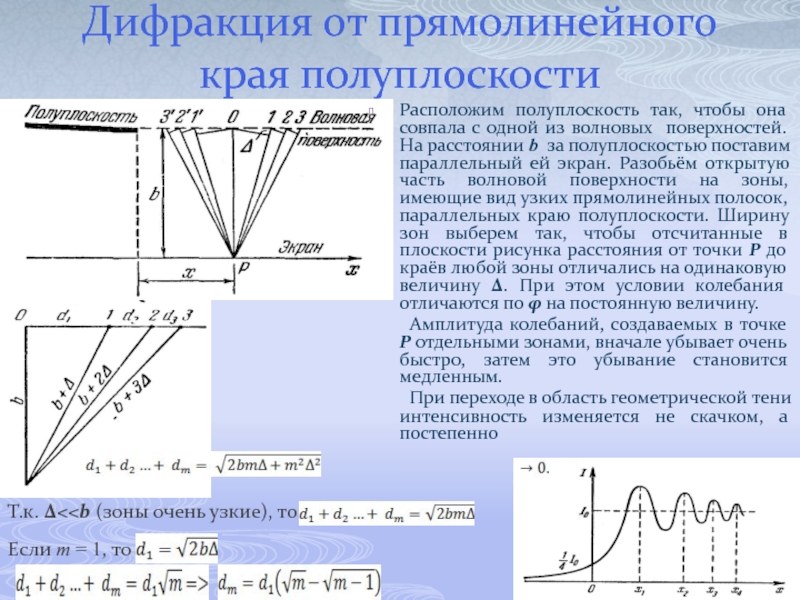
Слайд 39Дифракция от прямолинейного края полуплоскости
Расположим полуплоскость так, чтобы она совпала с
Амплитуда колебаний, создаваемых в точке Р отдельными зонами, вначале убывает очень быстро, затем это убывание становится медленным.
При переходе в область геометрической тени интенсивность изменяется не скачком, а постепенно
Т.к. Δ<
Если m = 1, то
Слайд 40Зонная пластинка
Пластинка, перекрывающая четные зоны.
Колебания от четных и
Слайд 41ЙОЗЕФ ФРАУНГОФЕР (1787 – 1826 ГГ.) – НЕМЕЦКИЙ ФИЗИК, ОПТИК, ИЗ
Дифракция Фраунгофера
(дифракция в параллельных лучах)
Слайд 42Дифракция Фраунгофера на одной щели
Плоская монохроматическая волна падает нормально плоскости узкой
? = NF = аsin?,
где F – основание перпендикуляра, опущенного из т. М на луч ND.
Открытую часть волновой поверхности в плоскости щели MN разбивают на зоны Френеля, имеющие вид полос. Ширина каждой зоны выбирается так, чтобы ? = ?/2. Все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе, т.к. плоскость щели совпадает с волновым фронтом (свет падает нормально). Амплитуды вторичных волн равны, т.к. зоны Френеля одинаковы по площади и одинаковы наклонены к направлению наблюдения.
Если число зон Френеля четное, то
а sin? = ±2m?/2 (m = 1, 2, 3, …)
в т. В – дифракционный минимум (полная темнота)
Если число зон Френеля нечетное, то
а sin? = ± (2m + 1)?/2 (m = 1, 2, 3, …) – дифракционный максимум.
? = 0 : щель действует как одна зона Френеля (в т. В0 – центральный дифракционный максимум).
При сужении щели центральный максимум расширяется с уменьшением его яркости. При расширении щели (а>?) дифракционные полосы сужаются и становятся ярче с увеличением их числа. При а>>? в центре – резкое изображение источника света. При а = ? (sin ? = 1): центральный максимум расплывается в бесконечность и экран освещен равномерно. При а≲? приближенный метод Френеля не применяют, т.к. волновое поле в плоскости щели нельзя отождествлять с неискаженным полем падающей волны.
Слайд 43Дифракционная решетка – система параллельных щелей равной ширины, лежащих в одной
Постоянная (период) решетки:
d = a+b,
где а – ширина щели;
b – ширина непрозрачных
промежутков.
В тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть прежние (главные) минимумы интенсивности будут наблюдаться в направлениях:
Вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, то есть возникнут дополнительные минимумы. Дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода λ/2; 3λ/2, …
Δ = CF = (a+b)sinφ => Δ = d sinφ
Если дифракционная решетка состоит из N щелей, то
условие главных min:
условие главных max:
условие дополнительного минимума:
условие дополнительных минимумов
условие главных максимумов
Т. е. между двумя главными максимумами располагается один дополнительный минимум.
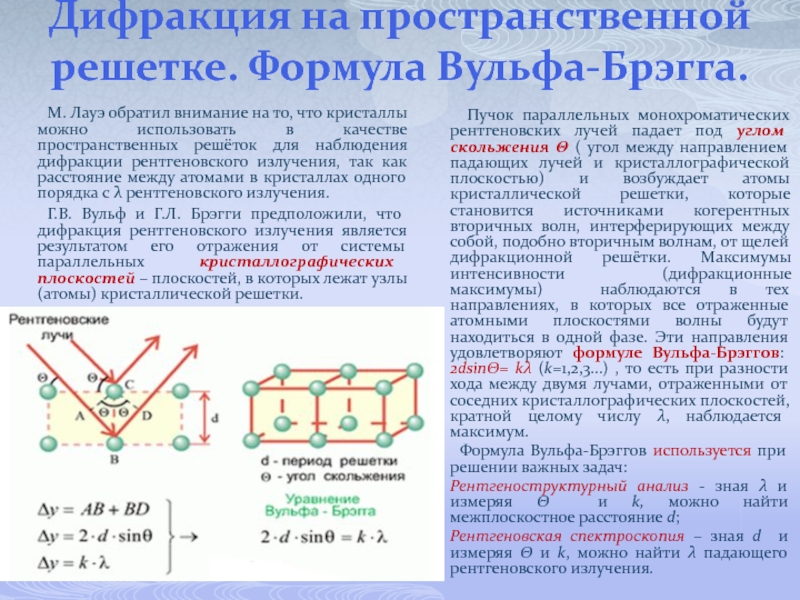
Слайд 44Дифракция на пространственной решетке. Формула Вульфа-Брэгга.
М. Лауэ обратил внимание на то,
Г.В. Вульф и Г.Л. Брэгги предположили, что дифракция рентгеновского излучения является результатом его отражения от системы параллельных кристаллографических плоскостей – плоскостей, в которых лежат узлы (атомы) кристаллической решетки.
Пучок параллельных монохроматических рентгеновских лучей падает под углом скольжения Θ ( угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становится источниками когерентных вторичных волн, интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решётки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одной фазе. Эти направления удовлетворяют формуле Вульфа-Брэггов: 2dsinΘ= kλ (k=1,2,3…) , то есть при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу λ, наблюдается максимум.
Формула Вульфа-Брэггов используется при решении важных задач:
Рентгеноструктурный анализ - зная λ и измеряя Θ и k, можно найти межплоскостное расстояние d;
Рентгеновская спектроскопия – зная d и измеряя Θ и k, можно найти λ падающего рентгеновского излучения.
Слайд 46Естественный и поляризованный свет
Следствием теории Максвелла является поперечность световых волн. Вектор
Для получения поляризованного света используют приборы, пропускающие колебания только определенного направления вследствие анизоторопности среды, являющейся основной рабочей частью устройства (например, турмалин) – поляризаторы. Они свободно пропускают колебания, параллельные плоскости, которую мы будем называть плоскостью поляризатора, и полностью или частично задерживают колебания, перпендикулярные к его плоскости. Поляризатор, частично задерживающий перпендикулярные к его плоскости колебания, называется несовершенным. Свет, который получается на выходе из несовершенного поляризатора, частично поляризован (смесь естественного и плоскополяризованного света).
Слайд 47Степень поляризации
Если пропустить частично поляризованный свет через поляризатор, то при вращении
-
степень поляризации
Для плоскопляризованного света:
Imin = 0; P = 1
Для естественного света:
Imin = Imax; Р = 0
Слайд 48
Этьен Луи Малюс
(1775 – 1812 гг.)
– французский физик.
Колебания
I = Icos2φ, где I – интенсивность колебания с амплитудой А.
В естественном свете все φ равновероятны, следовательно, доля света, прошедшего через поляризатор, будет равна среднему значению cos2φ , т.е. ½.
Пусть на поляризатор падает плоскополяризованный свет амплитудой А0 и интенсивностью I0. Сквозь прибор пройдет составляющая с А = А0cosφ, где φ – угол между плоскостью колебаний падающего света и плоскостью поляризатора.
Закон Малюса (1809 г.)
Слайд 49Поляризация при отражении и преломлении. Закон Брюстера (1815 г.).
Если угол падения
Закон Брюстера: tgϴБр = n21
При угле падения ϴБр, отраженный луч полностью поляризован (содержит только колебания, перпендикулярные к плоскости падения). Степень поляризации преломленного луча при угле падения, равном ϴБр, достигает наибольшего значения, однако этот луч остается поляризованным только частично. При падении света под углом ϴБр, отраженный луч перпендикулярен преломленному.
Дэвид Дэвид Брюстер
(1781 – 1868 гг.) –
шотландский физик.
Слайд 50Двойное лучепреломление – разделение упавшего на прозрачные кристаллы (кроме кристаллов кубической
Расмус (Эразм) Бартолин (1625 – 1698 гг.) – датский ученый впервые открыл в 1669 г. для исландского шпата явление двойного лучепреломления.
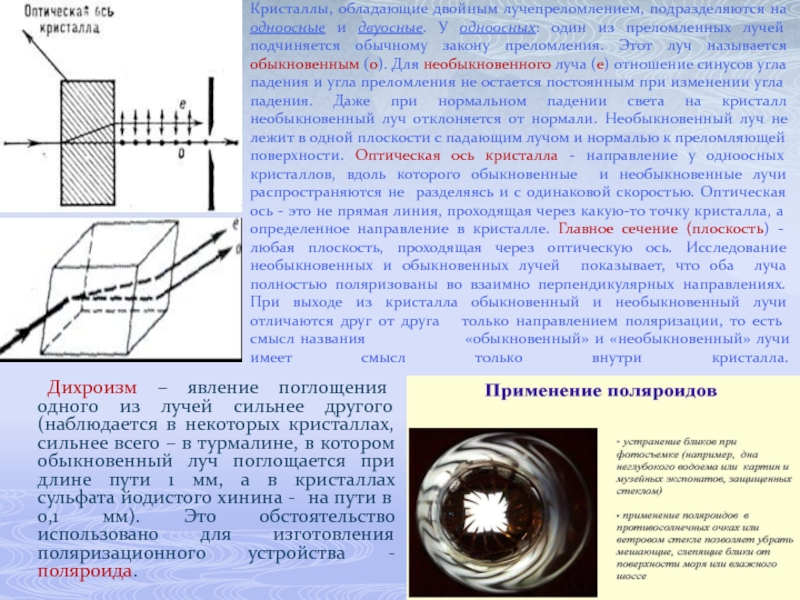
Слайд 51Кристаллы, обладающие двойным лучепреломлением, подразделяются на одноосные и двуосные. У одноосных:
Дихроизм – явление поглощения одного из лучей сильнее другого (наблюдается в некоторых кристаллах, сильнее всего – в турмалине, в котором обыкновенный луч поглощается при длине пути 1 мм, а в кристаллах сульфата йодистого хинина - на пути в 0,1 мм). Это обстоятельство использовано для изготовления поляризационного устройства - поляроида.
Слайд 52 Двойное лучепреломление объясняется анизотропией кристаллов. В кристаллах некубической системы диэлектрическая
Волновая поверхность необыкновенных лучей – эллипсоид вращения. В местах пересечения с оптической осью кристалла этот эллипсоид и сфера (для обыкновенных лучей) соприкасаются. Эллипсоид необыкновенного луча вписан в сферу обыкновенного луча (эллипсоид скоростей вытянут вдоль оптической оси) – положительный кристалл. Эллипсоид описан вокруг сферы (эллипсоид скоростей растянут в направлении, перпендикулярном оптической оси) – отрицательный кристалл.
-
В зависимости от того, какая из этих скоростей, vo или ve, больше, различают положительные и отрицательные кристаллы.
Слайд 53Прохождение плоскополяризованного света через кристаллическую пластинку За время прохождения через пластинку между
Пластинка в четверть волны
Вырезанная параллельно оптической оси пластинка, для которой оптическая разность хода:
(no – ne)d = mλ0 + λ0/4, где (m = 0,1,2,…)
называется пластинкой в четверть волны (пластинкой λ/4).
Плоскополяризованный свет, пройдя такую пластику, превращается в эллиптически поляризованный.
При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают .
Если на пути эллиптически поляризованного света поставить пластинку в λ/4, расположив её оптическую ось вдоль одной из осей эллипса, то пластинка внесет дополнительную разность фаз π/2, следовательно, разность фаз двух плоскополяризованных волн, дающих в сумме эллиптически поляризованную волну, станет равной 0 или π, так что наложение этих волн даст плоскополяризованную волну.
Пластинка в полволны
Вырезанная параллельно оптической оси пластинка, для которой оптическая разность хода:
(no – ne)d = mλ0 + λ0/2, где (m = 0,1,2,…)
называется пластинкой в полволны (пластинкой λ/2).
Слайд 55ЯВЛЕНИЯ, ОБУСЛОВЛЕННЫЕ ЗАВИСИМОСТЬЮ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ВЕЩЕСТВА ОТ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ
Дисперсия света
(открыта И. Ньютоном
в 1672 г.)
Слайд 56D = показывает как быстро изменяется показатель преломления
n = f(λ0),
где λ0 –
длина света
в вакууме.
Для всех прозрачных бесцветных веществ показатель преломления уменьшается с увеличением длин волны. Такая дисперсия носит название нормальной. Если же показатель преломления увеличивается с увеличением длины волны, то такая дисперсия носит название аномальной.
Различия в дифракционном и призматическом спектрах
1) Дифракционная решетка разлагает падающий свет непосредственно по длинам волн λ, следовательно, по измеряемым углам (по направлениям соответственных максимумов) можно вычислить длину волны λ. Разложение света в спектр в призме происходит по значениям n, следовательно, чтобы определить длину волны λ, надо знать n= f (λ).
2) dsinφ = ± 2mλ/2 = ± m λ => sinφ ~ λ => красные лучи отклоняются при прохождении через дифракционную решетку сильнее, чем фиолетовые. В случае дисперсионного разложения показатель преломления n уменьшается при росте длины волны λ, следовательно, красные лучи отклоняются слабее, чем фиолетовые.
Слайд 57Электронная теория дисперсии света
В оптической области спектра для всех веществ
В теории Лоренца дисперсия света рассматривается как результат взаимодействия ЭМВ с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны. Применим теорию Лоренца для однородного диэлектрика.
где ε0 – электрическая постоянная,
– мгновенное значение поляризованности (n0 – концентрация атомов в диэлектрике). В первом приближении считаем, что вынужденные колебания совершают только внешние – оптические электроны.
Уравнение вынужденных колебаний электрона:
, где F0 = eE0 –
амплитудное значение силы, действующей на электрон со стороны поля волны;
- собственная частота колебаний
электрона; m – масса электрона.
Решение уравнения запишем в виде: х = Аcosωt,
где А = => =>
В области ω = (0;ω0) n2 > 1;
В области ω = ω0 n2 = ±∞; в области ω = (ω0;∞) n2 < 1.
.
Слайд 58Поглощение (абсорбция) света - явление уменьшения энергии световой волны при её
Пьер Бугер
(1698 – 1758 гг.)
– французский
Физик
Линейчатый спектр поглощения
Для одноатомных газов и паров металлов α―>0 и лишь для очень узких областей (~10-12 – 10-11 м) наблюдаются резкие максимумы, которые соответствуют частотам собственных колебаний электронов в атомах. Для молекул - полосы поглощения шириной ≈ 10-10 – 10-7 м.
Закон Бугера: I = I0e-αx, где I0 и I – интенсивности плоской монохроматической световой волны соответственно на входе и выходе слоя поглощающего вещества толщиной х; α – коэффициент поглощения (зависит от λ, химической природы и состояния вещества, не зависит от интенсивности света). При х = 1/α интенсивность света I по сравнению с I0 уменьшается в е раз.
Металлы практически непрозрачны, т.к. в металлах возникают быстропеременные токи из-за наличия свободных электронов и энергия световой волны превращается во внутреннюю энергию металла.
Сплошной спектр поглощения
Для диэлектриков α = 10-3 – 10-5 см-1. У них наблюдается селективное поглощение в определенных интервалах λ, когда α резко возрастает, и наблюдаются широкие полосы поглощения. В диэлектриках нет свободных электронов, поэтому поглощение происходит вследствие резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах.
Слайд 59Рассеяние света –
дифракция на мелких неоднородностях
Световые волны, дифрагируя на
Колебания электронов, вызванные рассеиваемым световым пучком, происходят в плоскости, перпендикулярной к пучку. Свет, рассеиваемый частицами в направлениях, перпендикулярных к пучку, будет полностью поляризован. В направлениях, образующих с пучком угол, отличный от прямого, рассеянный свет поляризован частично.
В результате рассеяния света в боковых направлениях интенсивность в направлении распространения убывает быстрее, чем в случае одного поглощения, следовательно:
для мутной среды: I = I0e-(α + α’)x , где
α’ – коэффициент экстинкции, обусловленный рассеянием.
Если размеры неоднородностей малы по сравнению с λ (не более 0,1 λ), то интенсивность рассеянного света пропорциональна четвертой степени частоты (обратно пропорциональна четвертой степени длины волны):
I ~ ω4 ~ 1/λ4 - закон Рэлея.
Если размеры неоднородностей сравнимы с λ, то электроны, находящиеся в различных местах неоднородности, колеблются с заметным сдвигом по φ=> I~ω2.
Слайд 60Эффект Вавилова-Черенкова (1934 г.)
С.И. Вавилов (1892 – 1951 гг.) –основатель отечественной
Согласно электромагнитной теории, заряженная частица излучает ЭМВ лишь при движении с ускорением. И.Е. Тамм и И.М. Франк показали, что это утверждение справедливо до тех пор, пока скорость заряженной частицы не превышает фазовой скорости ЭМВ. Если частица движется со скоростью, большей фазовой для этой среды, то она излучает ЭМВ. Особенность данного эффекта: распространение излучения только по направлениям, составляющим острый угол ϑ с траекторией частицы, т.е. вдоль образующих конуса, ось которого совпадает с направлением скорости частицы.
В излучении Вавилова – Черенкова преобладают короткие волны => оно окрашено в голубой цвет.
П.А. Черенков
(1904 – 1990 гг.) – советский физик, лауреат Нобелевской премии (1958 г.) совместно с И.Е. Таммом и И.М. Франком за объяснение эффекта Вавилова - Черенкова.
cosϑ = c/nv