- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Охлаждение, нагревание тел конечных размеров. Нагрев параллелепипеда презентация
Содержание
- 1. Охлаждение, нагревание тел конечных размеров. Нагрев параллелепипеда
- 2. Нагрев параллелепипеда Заготовка (параллелепипед) с
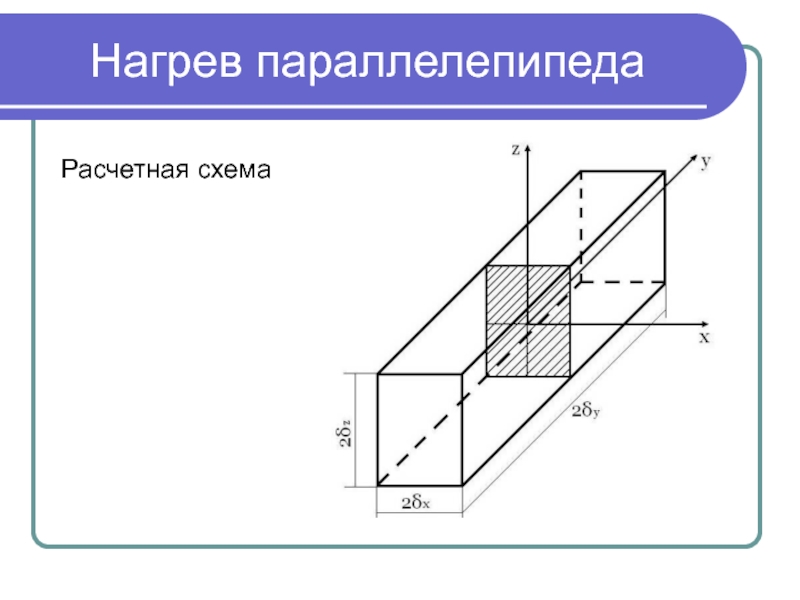
- 3. Нагрев параллелепипеда Расчетная схема
- 4. Нагрев параллелепипеда Дифференциальное уравнение температурного поля при
- 5. Начальные условия Считаем, что в начале процесса
- 6. Граничные условия Из условий геометрической и
- 7. Граничные условия Теплообмен на поверхности заготовки
- 8. Решение Решение системы (1)-(8) в безразмерном виде
- 9. Температура где
- 10. Температура
- 11. Температура Решение задачи о равномерном нагреве пластины известно:
- 12. Характеристические уравнения Значения
- 13. Температура Решение задачи можно выразить через безразмерные
- 14. Безразмерные величины где:
- 15. Средняя температура Средняя температура заготовки (параллелепипеда) определяется
- 16. Средняя температура где:
- 17. Охлаждение длинного прямоугольного стержня Пусть стержень имеет
- 18. Охлаждение длинного прямоугольного стержня
- 19. .
- 20. .
- 21. .
- 22. .
- 23. .
- 24. .
- 25. .
- 26. .
- 27. .
- 28. .
- 29. .
- 30. .
- 31. .
- 32. .
- 33. Охлаждение цилиндра конечной длины Ограниченный цилиндр можно
- 34. Охлаждение цилиндра конечной длины Температура:
- 35. Охлаждение цилиндра конечной длины Характеристические уравнения:
- 36. Охлаждение цилиндра конечной длины Температура:
- 37. .
- 38. .
- 39. Средняя температура Средняя температура цилиндра конечных размеров
- 40. Вопросы к экзамену Охлаждение параллелепипеда. Охлаждение длинного прямоугольного стержня. Охлаждение цилиндра конечной длины.
Слайд 2Нагрев параллелепипеда
Заготовка (параллелепипед) с размерами
помещена в среду,
Слайд 4Нагрев параллелепипеда
Дифференциальное уравнение температурного поля при отсутствии внутренних источников теплоты имеет
(1)
Слайд 5Начальные условия
Считаем, что в начале процесса температура в заготовке распределена равномерно,
(2)
Слайд 7Граничные условия
Теплообмен на поверхности заготовки подчиняется закону Ньютона-Рихмана:
(7)
(8)
Слайд 8Решение
Решение системы (1)-(8) в безразмерном виде можно представить как произведение трех
Слайд 15Средняя температура
Средняя температура заготовки (параллелепипеда) определяется также как произведение трех температур
Слайд 17Охлаждение длинного прямоугольного стержня
Пусть стержень имеет ограниченные размеры в направлении осей
Данное тело можно представить как результат пересечения двух неограниченных пластин во взаимно перпендикулярном направлении.
Слайд 18Охлаждение длинного прямоугольного стержня
.
Дифференциальное уравнение температурного поля при отсутствии внутренних источников
(1)
Слайд 19.
Начальные условия
Считаем, что в начале процесса температура в стержне распределена равномерно,
(2)
Слайд 21.
.
Граничные условия
Теплообмен на поверхности стержня подчиняется закону Ньютона-Рихмана:
(5)
(6)
Слайд 28.
.
Средняя температура
Средняя температура стержня определяется также как произведение трех температур для
Слайд 30.
.
Охлаждение цилиндра конечной длины
Пусть внутри источник теплоты отсутствует:
Пусть
Тогда дифференциальное уравнение
(1)