движения точки
§ 2. Теорема моментов
§ 3. Работа силы
3.1. Элементарная работа силы
3.2. Работа силы на конечном перемещении
3.3. Примеры вычисления работы силы
§ 4. Теорема об изменении кинетической энергии материальной точки
§ 5. Несвободное движение точки (Принцип Даламбера)
5.1. Принцип Даламбера
5.2. Относительное движение точки
5.3. Частные случаи
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общие теоремы динамики точки презентация
Содержание
- 1. Общие теоремы динамики точки
- 2. Количеством движения материальной точки называется векторная
- 3. Импульс силы за некоторый промежуток времени
- 4. § 1. Теорема об изменении количества движения
- 5. Теорема об изменении количества движения точки (в
- 6. Если задача пространственная (1-я задача динамики)
- 7. § 2. Теорема моментов Моментом количества
- 8. Продифференцируем момент количества движения по времени или
- 9. Основное уравнение динамики умножим слева векторно на радиус-вектор или
- 10. Спроектируем обе части равенства на ось Z,
- 11. Если то Момент количества движения точки
- 12. Пример. Рассмотрим движение материальной точки под действием центральной силы из (¤) =>
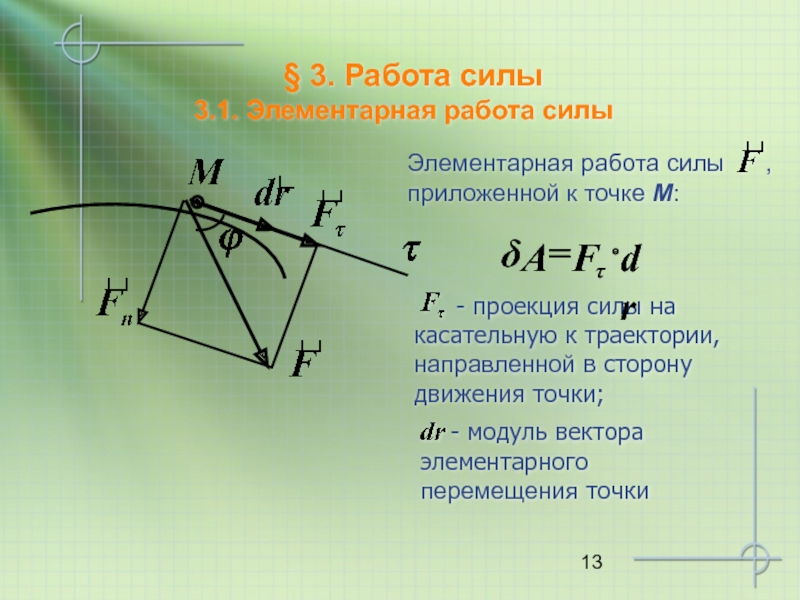
- 13. § 3. Работа силы 3.1. Элементарная работа силы
- 14. δA > 0, если Fτ > 0
- 15. тогда ( * ) – аналитическое
- 16. 3.2. Работа силы на конечном перемещении
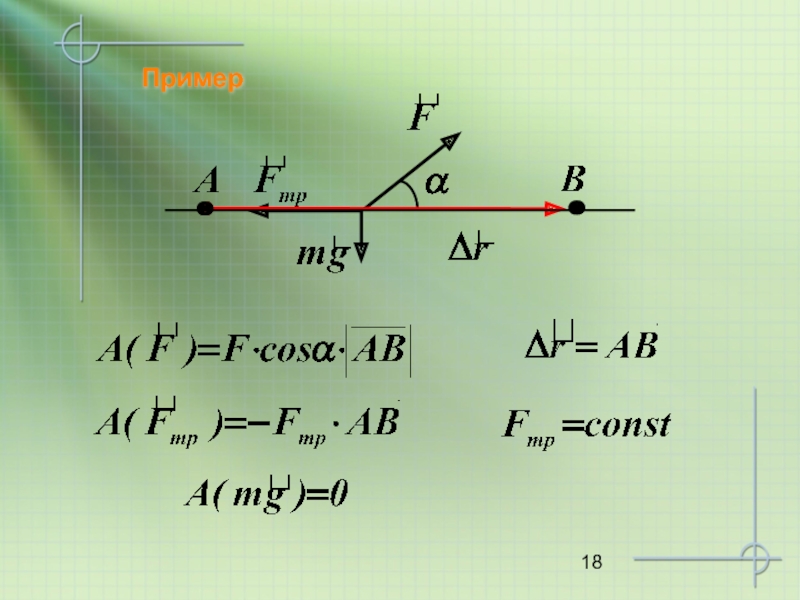
- 17. 3.3. Примеры вычисления работы силы а) Работа постоянной силы на конечном перемещении (1)
- 18. Пример
- 19. б) Работа силы тяжести Воспользуемся (1) и вычислим работу силы тяжести на перемещении AB: или
- 20. в) Работа линейной силы упругости
- 21. § 4. Теорема об изменении кинетической энергии
- 22. Кинетической энергией материальной точки называется скалярная величина,
- 23. Интегрируем (5): Изменение кинетической энергии материальной точки
- 24. § 5 Несвободное движение точки (Принцип Даламбера)
- 25. Жа́н Леро́н Д’Аламбе́р (фр. Jean Le
- 26. 5.1. Принцип Даламбера - векторную
- 27. - уравнение принципа Даламбера Если
- 28. Можно применять и для системы материальных точек,
- 29. 5.2. Относительное движение точки Основной
- 30. Все уравнения и теоремы механики для относительного
- 31. если точка по отношению к подвижным
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость Элементарным импульсом силы называется векторная величина, равная произведению силы на элементарный промежуток времени
Слайд 2 Количеством движения материальной точки называется векторная величина, равная произведению массы
точки на ее скорость
Элементарным импульсом силы называется векторная величина, равная произведению силы на элементарный промежуток времени
Слайд 3 Импульс силы за некоторый промежуток времени равен определенному интегралу от
элементарного импульса, взятого по этому промежутку
В случае постоянной силы
В случае движения матер. точки в пространстве
Импульс силы характеризует действие силы на материальную точку за время τ
Слайд 4§ 1. Теорема об изменении количества движения точки
(в дифференциальной форме)
Производная по
времени от количества движения точки равна сумме действующих на нее сил
Слайд 5Теорема об изменении количества движения точки
(в интегральной форме)
Изменение количества движения точки
за некоторый промежуток времени равно сумме импульсов всех действующих на нее сил за тот же промежуток времени
Слайд 6Если задача пространственная
(1-я задача динамики)
Зная, как изменяется скорость
точки, определить импульс действующих сил
(2-я задача динамики)
Зная импульсы действующих сил, определить, как изменяется скорость точки при движении
(2-я задача динамики)
Зная импульсы действующих сил, определить, как изменяется скорость точки при движении
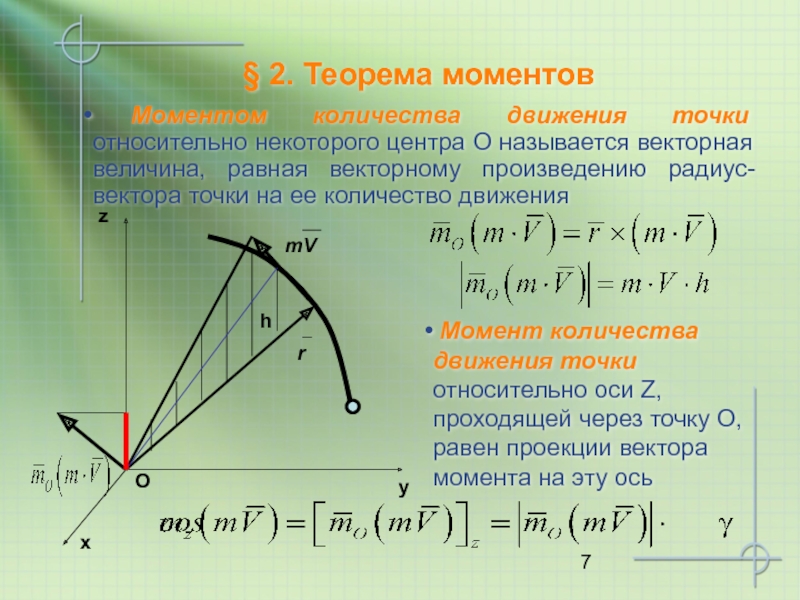
Слайд 7§ 2. Теорема моментов
Моментом количества движения точки относительно некоторого центра
О называется векторная величина, равная векторному произведению радиус-вектора точки на ее количество движения
Момент количества движения точки относительно оси Z, проходящей через точку О, равен проекции вектора момента на эту ось
h
Слайд 8Продифференцируем момент количества движения по времени
или
Теорема моментов относительно центра
Производная по времени
от момента количества движения точки, взятого относительно неподвижного центра, равна моменту действующей на точку силы относительно того же центра
Слайд 10Спроектируем обе части равенства на ось Z, получим
Теорема моментов относительно оси
Производная
по времени от момента количества движения точки, взятого относительно некоторой оси Z, равна моменту действующей на точку силы относительно той же оси
Слайд 11Если
то
Момент количества движения точки относительно некоторого центра есть величина постоянная, если
момент действующей на точку силы относительно того же центра равен нулю
Теорема сохранения момента количества движения
(¤)
Слайд 14δA > 0, если Fτ > 0
Поскольку Fτ = m·aτ =
m dV/dt , то работа силы характеризует действие силы по изменению величины скорости точки
Fτ = Fcosφ, тогда δA = Fcosφ·dr
Элементарная работа равна скалярному произведению вектора силы на вектор элементарного перемещения точки ее приложения
δA < 0, если Fτ < 0
δA = 0, если Fτ = 0
Слайд 16 3.2. Работа силы на конечном перемещении
Работа силы на конечном перемещении
есть предел суммы элементарных работ
или
Работа силы на конечном перемещении AB равна взятому вдоль этого перемещения криволинейному интегралу от элементарной работы
Слайд 19б) Работа силы тяжести
Воспользуемся (1) и вычислим работу силы тяжести на
перемещении AB:
или
Слайд 21§ 4. Теорема об изменении кинетической энергии материальной точки
, тогда
Дифференциал кинетической
энергии материальной точки равен элементарной работе всех сил, действующих на точку
Слайд 22Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы
точки на квадрат ее скорости
Слайд 23Интегрируем (5):
Изменение кинетической энергии материальной точки на некотором ее перемещении равно
сумме работ сил, действующих на точку на этом же перемещении
Слайд 24§ 5 Несвободное движение точки
(Принцип Даламбера)
Уравнения движения или условия
равновесия можно получить, положив в основу другие общие положения, называемые принципами механики
Предложил их в XVIII веке французский ученый Жан Лерон Д’Аламбер
Слайд 25Жа́н Леро́н Д’Аламбе́р (фр. Jean Le Rond d'Alembert; 16 ноября 1717
—
29 октября 1783) французский философ, механик и математик
Слайд 26 5.1. Принцип Даламбера
- векторную величину, равную по модулю ma
и направленную в противоположную сторону ускорения, называют силой инерции
Слайд 27- уравнение принципа Даламбера
Если движущуюся точку в некоторый момент
времени остановить, приложив к ней силу инерции, то образовавшаяся совокупность сил – активной, реакции связи и силы инерции – будет представлять собой уравновешенную систему сил
Слайд 28Можно применять и для системы материальных точек, только необходимо помнить, что
никакие
реальные силы инерции на точку не действуют, это фиктивные силы
никакого равновесия нет, а есть движение, и уравнения статики записываются формально
силы инерции вводят только тогда, когда для решения задачи применяют принцип Даламбера
никакого равновесия нет, а есть движение, и уравнения статики записываются формально
силы инерции вводят только тогда, когда для решения задачи применяют принцип Даламбера
Слайд 29
5.2. Относительное движение точки
Основной закон динамики, общие теоремы и уравнение
принципа Даламбера выполняются только в инерциальных системах отсчета!!!
Слайд 30Все уравнения и теоремы механики для относительного движения точки составляются так
же, как уравнения абсолютного движения, если при этом к действующим на точку силам добавить переносную и кориолисову силы инерции!
5.3. Частные случаи
если подвижные координатные оси движутся поступательно, то
если подвижные координатные оси перемещаются поступательно, равномерно и прямолинейно, то
