- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общие теоремы динамики точки презентация
Содержание
- 1. Общие теоремы динамики точки
- 2. Цель лекции Цель лекции Ознакомиться с
- 3. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ Введение теоремы об
- 4. ИМПУЛЬС ТОЧКИ Теорема об изменении импульса
- 5. ИМПУЛЬС СИЛЫ Теорема об изменении импульса
- 6. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ИМПУЛЬСА Теорема об изменении
- 7. ДОКАЗАТЕЛЬСТВО Теорема об изменении импульса
- 8. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА Теорема об изменении
- 9. ПРИМЕР Теорема об изменении импульса
- 10. МОМЕНТ ИМПУЛЬСА ТОЧКИ Момент
- 11. МОМЕНТ ИМПУЛЬСА ТОЧКИ Теорема об изменении момента импульса O
- 12. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА ИМПУЛЬСА Производная по
- 13. ДОКАЗАТЕЛЬСТВО Теорема об изменении момента импульса
- 14. ПРОЕКЦИИ МОМЕНТА ИМПУЛЬСА Теорема об изменении момента импульса
- 15. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Теорема об
- 16. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ
- 17. ДВИЖЕНИЕ ПЛАНЕТ ?
- 18. ДВИЖЕНИЕ ПЛАНЕТ Теорема об изменении момента
- 19. ДВИЖЕНИЕ ПЛАНЕТ Теорема об изменении момента импульса
- 20. ДВИЖЕНИЕ ПЛАНЕТ Теорема об изменении момента
- 21. ДВИЖЕНИЕ ПЛАНЕТ Теорема об изменении момента импульса Иоганн Кеплер (1571 - 1630)
- 22. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТОЧКИ- Теорема об изменении
- 23. РАБОТА СИЛЫ Теорема об изменении энергии
- 24. РАБОТА СИЛЫ
- 25. РАБОТА СИЛЫ Теорема об изменении энергии
- 26. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ЭНЕРГИИ Теорема об
- 27. ДОКАЗАТЕЛЬСТВО Теорема об изменении энергии Запишем
- 28. ДОКАЗАТЕЛЬСТВО Теорема об изменении энергии Умножим
- 29. ПРИМЕР Теорема об изменении энергии
- 30. ПРИМЕР Теорема об изменении энергии Будем
- 31. ПРИМЕР Теорема об изменении энергии Запишем
- 32. ПРИМЕР Теорема об изменении энергии Согласно
- 33. ПОТЕНЦИАЛЬНЫЕ СИЛЫ
- 34. ПОТЕНЦИАЛЬНЫЕ СИЛЫ
- 35. ПОТЕНЦИАЛЬНЫЕ СИЛЫ. ПРИМЕР Попробуем
- 36. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ Замечание Потенциал
- 37. ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Теорема об изменении импульса
- 38. РАБОТА ПОТЕНЦИАЛЬНЫХ СИЛ Теорема об изменении энергии
- 39. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ Заключение Какие из
- 40. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ Заключение Как происходит движение
- 41. ТЕМА СЛЕДУЮЩЕЙ ЛЕКЦИИ Заключение Динамика механической системы
Слайд 2Цель лекции
Цель лекции
Ознакомиться с общими теоремами динамики материальной точки и
План лекции
Введение
Теорема об изменении импульса точки
Теорема об изменении момента импульса точки
Движение в центральном поле
Теорема об изменении кинетической энергии точки
Работа силы. Потенциальные силы
Заключение
Слайд 3ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
Введение
теоремы об изменении …
импульса
момента импульса
кинетической энергии
Зачем нам нужны
оптимальная методика решения задач
на основе теорем динамики для точки
мы построим динамику механической системы
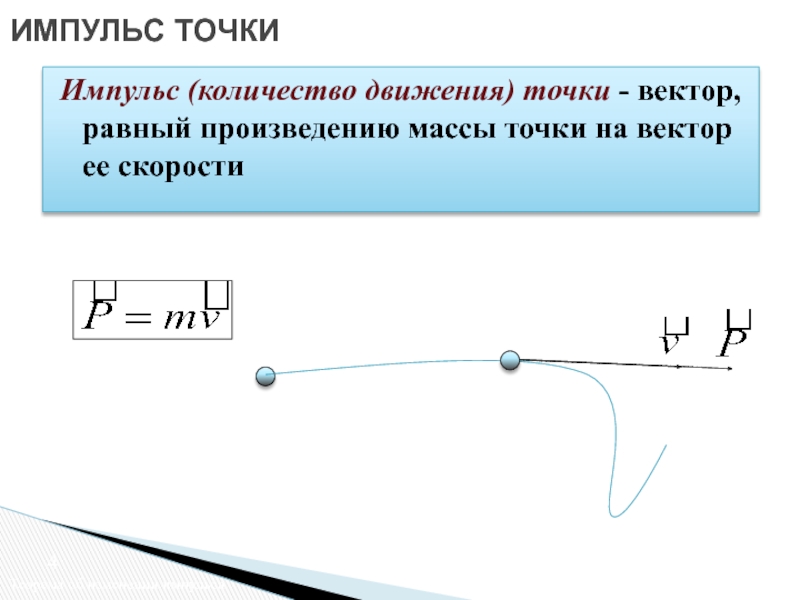
Слайд 4ИМПУЛЬС ТОЧКИ
Теорема об изменении импульса
Импульс (количество движения) точки - вектор, равный
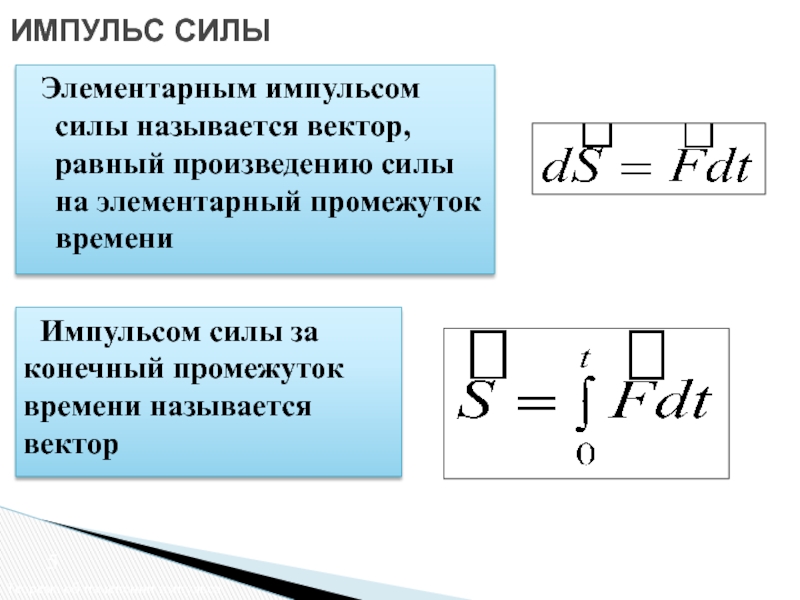
Слайд 5ИМПУЛЬС СИЛЫ
Теорема об изменении импульса
Элементарным импульсом силы называется вектор, равный
Импульсом силы за конечный промежуток времени называется вектор
Слайд 6ТЕОРЕМА ОБ ИЗМЕНЕНИИ ИМПУЛЬСА
Теорема об изменении импульса
Изменение импульса материальной точки
Производная по времени от импульса материальной точки равна равнодействующей приложенных к точке сил
Слайд 7ДОКАЗАТЕЛЬСТВО
Теорема об изменении импульса
Запишем дифф. уравнение движения точки
Учитывая
получим
или
Умножив обе части уравнения на элементарный промежуток времени и проинтегрировав, получим
или
Теорема доказана
Слайд 8ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Теорема об изменении импульса
Пусть
В этом случае
Если
Если проекция на какую-нибудь ось равнодействующей приложенных к точке сил равна нулю, то проекция импульса точки на эту ось сохраняется
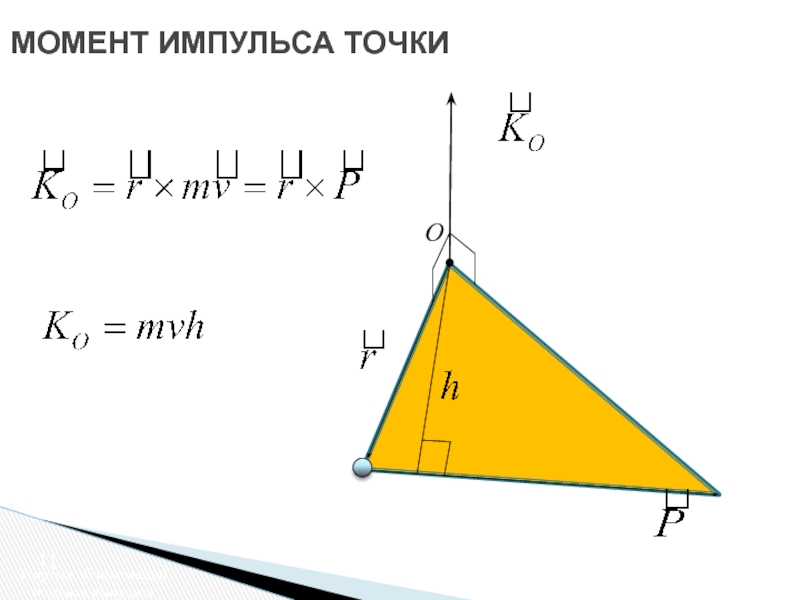
Слайд 10МОМЕНТ ИМПУЛЬСА ТОЧКИ
Момент импульса
(момент количества движения) точки -вектор, определяемый
равенством
- радиус-вектор точки, проведенный из центра O
Теорема об изменении момента импульса
Слайд 12ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА ИМПУЛЬСА
Производная по времени от момента импульса материальной
Теорема об изменении момента импульса
Слайд 13ДОКАЗАТЕЛЬСТВО
Теорема об изменении момента импульса
Запишем теорему об изменении
импульса
Рассмотрим выражение
Умножим обе части уравнения векторно на радиус-вектор точки
Теорема доказана
Таким образом,
Слайд 15ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Теорема об изменении момента импульса
Пусть
В этом
Если момент равнодействующей приложенных к материальной точке сил относительно какого-либо центра равен нулю, то момент импульса точки сохраняется
Слайд 16ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ
Действующую на материальную точку точку
?
Пример
Теорема об изменении момента импульса
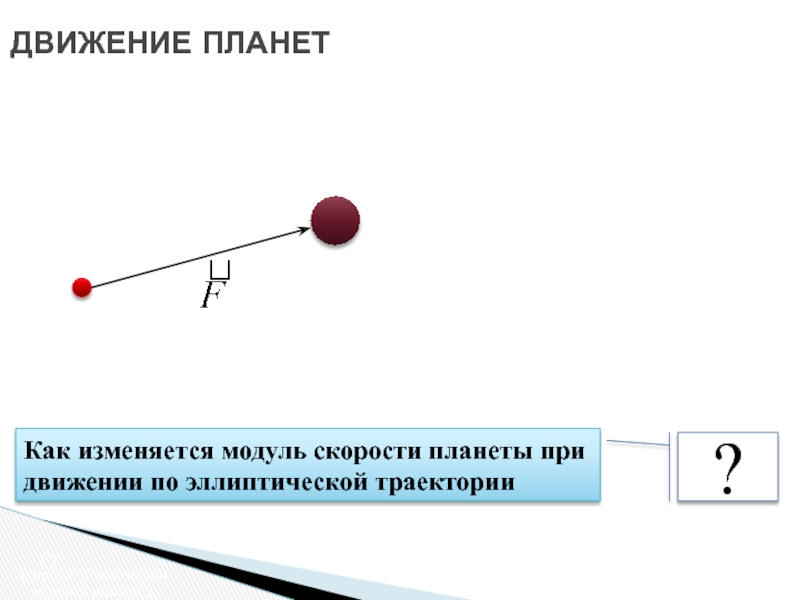
Слайд 17ДВИЖЕНИЕ ПЛАНЕТ
?
Как изменяется модуль скорости планеты при движении по эллиптической траектории
Теорема
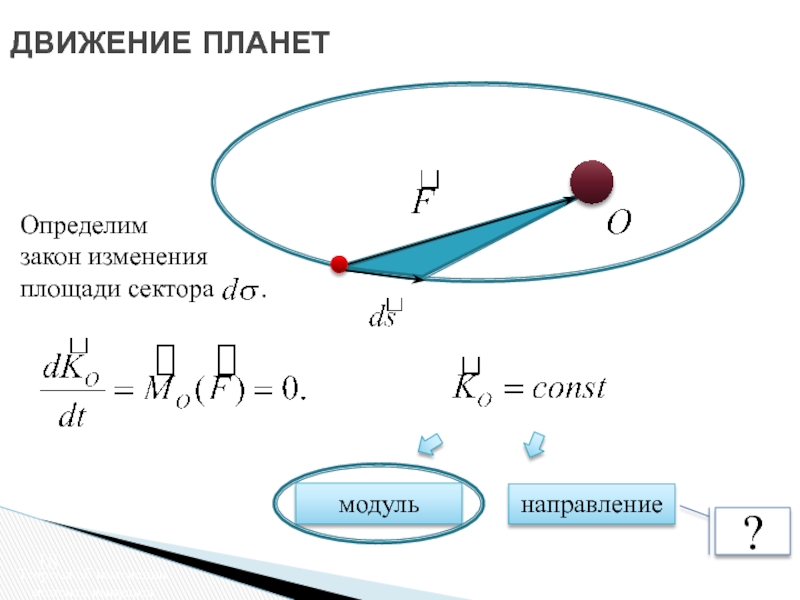
Слайд 18ДВИЖЕНИЕ ПЛАНЕТ
Теорема об изменении момента импульса
Определим
закон изменения
площади
модуль
направление
?
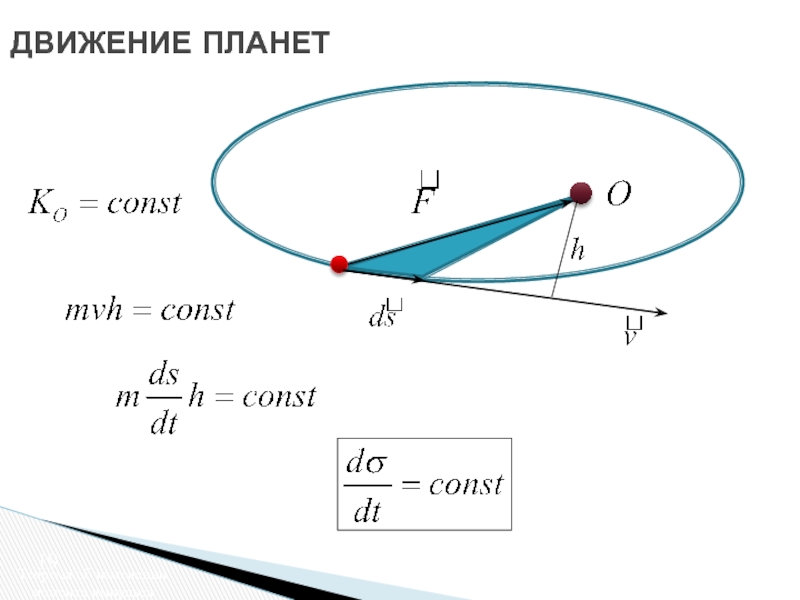
Слайд 20ДВИЖЕНИЕ ПЛАНЕТ
Теорема об изменении момента импульса
Каждая планета движется в плоскости, проходящей
Слайд 22КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТОЧКИ-
Теорема об изменении энергии
скалярная величина, равная половине
Слайд 25РАБОТА СИЛЫ
Теорема об изменении энергии
Элементарная работа силы –
величина, равная скалярному
Работа силы на конечном перемещении –
интеграл от элементарной работы, взятый вдоль этого перемещения
Слайд 26ТЕОРЕМА ОБ ИЗМЕНЕНИИ ЭНЕРГИИ
Теорема об изменении энергии
Изменение кинетической энергии точки на
Слайд 27ДОКАЗАТЕЛЬСТВО
Теорема об изменении энергии
Запишем дифф. уравнение движения точки
Спроектируем его на
Представим тангенциальное ускорение в виде
и учтем, что проекция силы
Слайд 28ДОКАЗАТЕЛЬСТВО
Теорема об изменении энергии
Умножим обе части уравнения на элементарное перемещение и
Теорема доказана
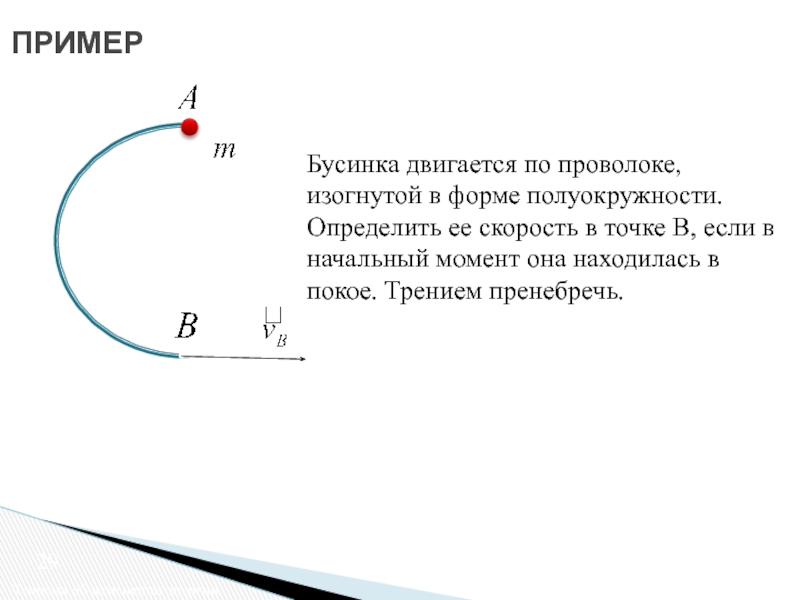
Слайд 29ПРИМЕР
Теорема об изменении энергии
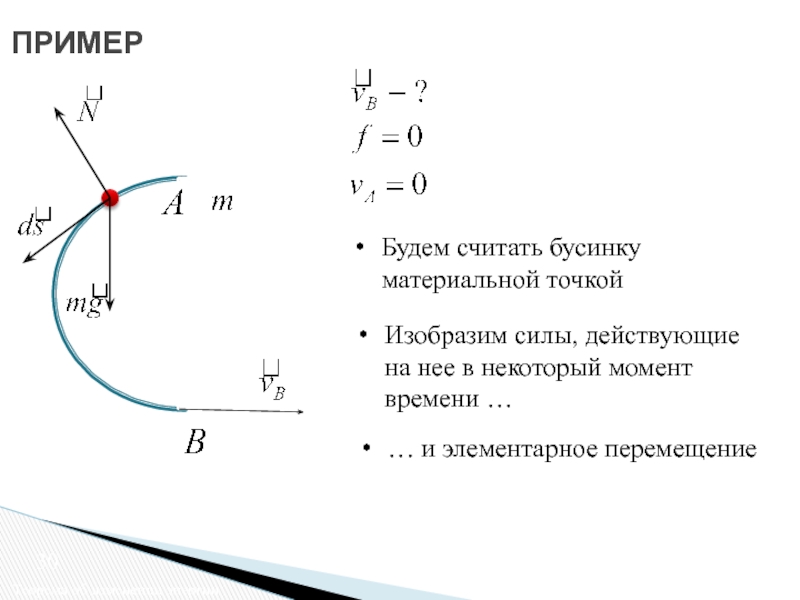
Бусинка двигается по проволоке, изогнутой в форме полуокружности.
Слайд 30ПРИМЕР
Теорема об изменении энергии
Будем считать бусинку материальной точкой
Изобразим силы, действующие
… и элементарное перемещение
Слайд 32ПРИМЕР
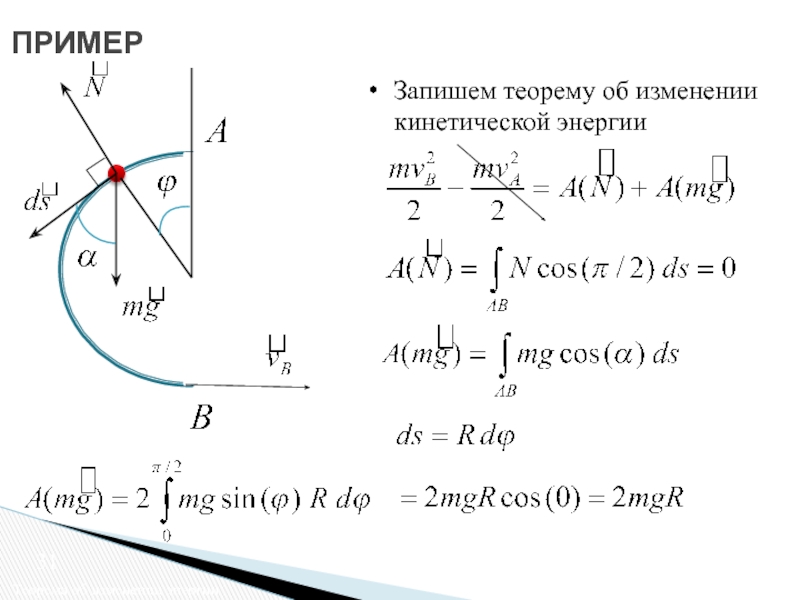
Теорема об изменении энергии
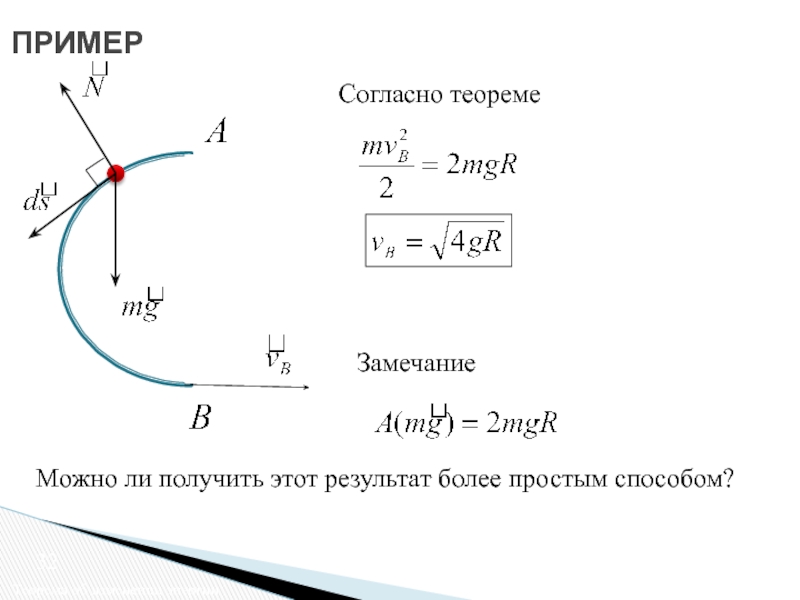
Согласно теореме
Замечание
Можно ли получить этот результат более простым
Слайд 33ПОТЕНЦИАЛЬНЫЕ СИЛЫ
Градиентом называется вектор с компонентами
Сила называется потенциальной (консервативной),
Теорема об изменении энергии
Слайд 34ПОТЕНЦИАЛЬНЫЕ СИЛЫ
Работа потенциальной силы не зависит от формы траектории точки
Теорема об изменении энергии
Слайд 35ПОТЕНЦИАЛЬНЫЕ СИЛЫ. ПРИМЕР
Попробуем построить потенциал для силы тяжести
Теорема об изменении энергии
Слайд 36ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Замечание
Потенциал определяется с точностью до некоторой не зависящей от
Потенциальной энергией точки, находящейся под действием консервативной силы, называется величина
Пусть
Теорема об изменении энергии
Слайд 37ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Теорема об изменении импульса
Для точки, находящейся под действием потенциальной
При движении точки она сохраняется.
Если на точку действует несколько потенциальных сил
Запишем теорему об изменении кинетической энергии для точки, находящейся под действием потенциальной силы
Слайд 39ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
Заключение
Какие из уравнений динамики точки записываются в виде векторных
Что такое импульс материальной точки?
Как определяется импульс силы за конечный промежуток времени?
При каких условиях количество движения системы не изменяется?
Как определяется и момент количества движения точки?
Чему равна проекция момента количества движения точки относительно центра на ось?
Слайд 40ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
Заключение
Как происходит движение материальной точки под действием центральной силы?
Как определяется работа постоянной силы на прямолинейном перемещении точки, к которой она приложена? А если сила переменная и точка перемещается по кривой?
Что понимают под элементарной работой силы и как она связана с работой силы на конечном перемещении точки, к которой она приложена? Когда элементарная работа равна нулю?