к.т.н., доц. Коротков Б.П.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общие понятия остойчивости презентация
Содержание
- 1. Общие понятия остойчивости
- 2. Рассмотренные вопросы 1. Общие понятия об
- 3. Знание, понимание и профессиональные навыки в соответствии
- 4. Знание, понимание и профессиональные навыки в соответствии
- 5. 1. Общие понятия об остойчивости
- 6. Остойчивостью называется способность плавающего судна, выведенного из
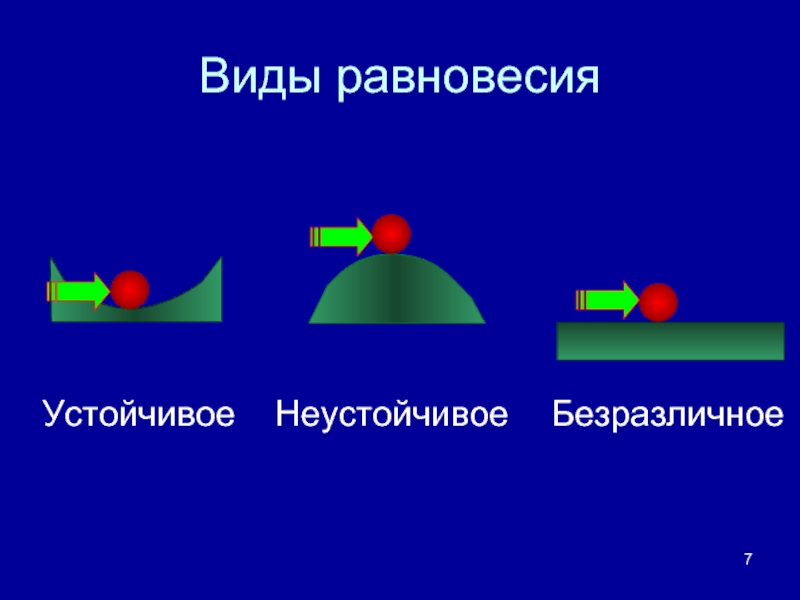
- 7. Виды равновесия Устойчивое Неустойчивое Безразличное
- 8. Начальная остойчивость – это остойчивость судна по
- 9. Признак начальной остойчивости Судно остойчиво, если после
- 10. Произвольное отклонение складывается из составляющих: - Вертикальное
- 11. Судно всегда остойчиво Судно в
- 12. Поперечное наклонение судна Судно остойчиво
- 13. Признак остойчивости равновесия судна Судно остойчиво, если оно остойчиво на всех возможных наклонениях
- 14. Определения - Ось наклонения – это линия
- 15. Ось, плоскость и угол наклонения След
- 16. 2. Равнообъемные наклонения
- 17. Равнообъемные наклонения При равнообъемных наклонениях величина погруженного
- 18. Произвольное наклонение судна Равнообъемное наклонение 2.
- 19. Признак остойчивости судна Судно является остойчивым, если
- 20. Выдающийся ученый, математик, механик и астроном, один
- 21. Могила Л. Эйлера на кладбище Александро-Невской Лавры
- 22. Теорема Эйлера о равнообъемных наклонениях: - Бесконечно близкие
- 23. Использование теоремы Эйлера Теорема Эйлера применима и
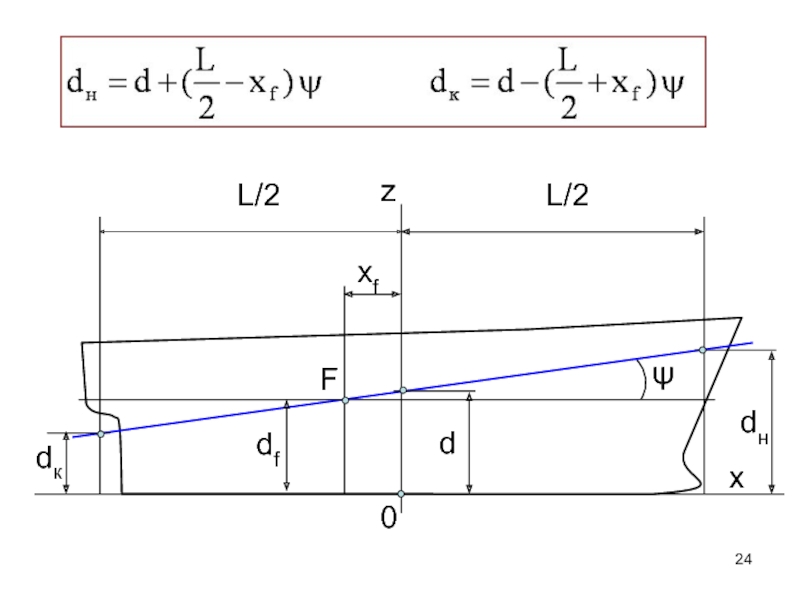
- 24. x xf d df dк dн z ψ 0 F
- 25. Уточненное определение объемного водоизмещения V при посадке
- 26. 3. Перемещения центра величины при равнообъемных наклонениях
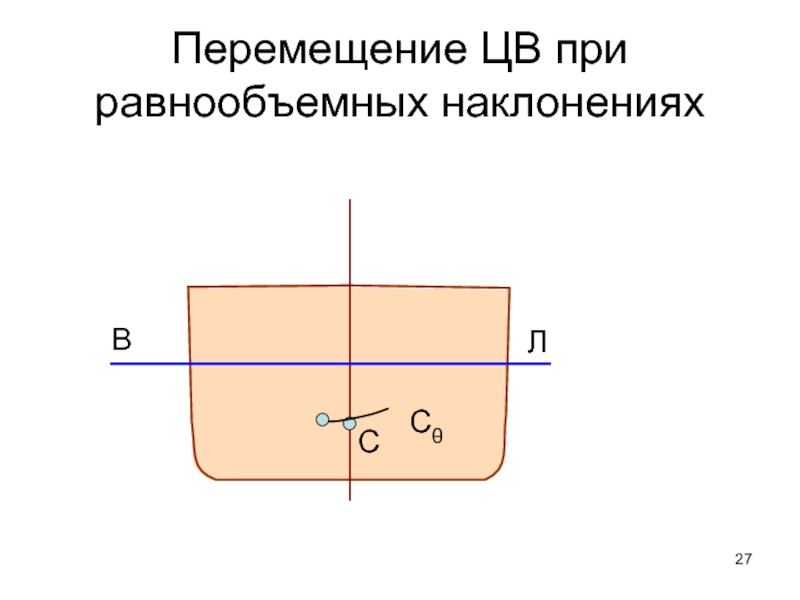
- 27. Перемещение ЦВ при равнообъемных наклонениях Сθ В Л
- 28. Приращения координат ЦВ при поперечном наклонении на
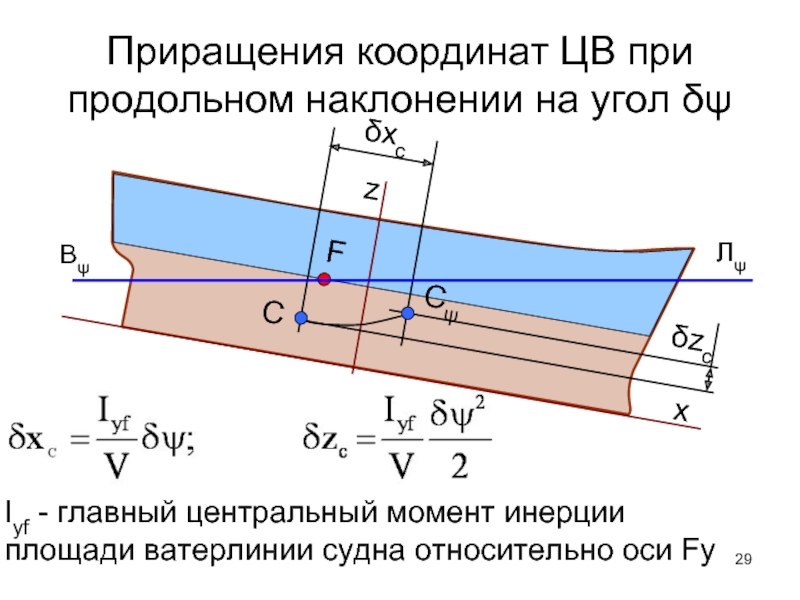
- 29. Приращения координат ЦВ при продольном наклонении на
- 30. Приращения координат ЦВ Моменты инерции характеризуют распределение
- 31. Уточнение xc судна, сидящего с дифферентом по
- 32. «Кривая С» При равнообъемных наклонениях ЦВ судна
- 33. Перемещения силы плавучести при наклонениях Сила плавучести
- 34. Перемещение ЦВ при равнообъемном поперечном наклонении на
- 35. Задание на самостоятельную работу: «Теория судна. Статика» п.п. 2.1, 2.2
- 36. Конец
Рассмотренные вопросы 1. Общие понятия об остойчивости 2. Равнообъемные наклонения 3. Перемещения центра величины при равнообъемных наклонениях
Слайд 1ГУМРФ им. адмирала С.О. Макарова
Факультет навигации и связи
Теория судна
Статика
Лекция №4
Общие понятия
остойчивости
Слайд 2Рассмотренные вопросы
1. Общие понятия об остойчивости
2. Равнообъемные наклонения
3. Перемещения центра величины
при равнообъемных наклонениях
Слайд 3Знание, понимание и профессиональные навыки в соответствии с минимальным стандартом компетентности
для вахтенных помощников капитана судов (в соответствии с ПДНВ)
Знание влияния груза, включая тяжеловесные грузы, на мореходность и остойчивость судна
Рабочее знание и применение информации об остойчивости, посадке и напряжениях, диаграмм и устройств для расчета напряжений в корпусе
Слайд 4Знание, понимание и профессиональные навыки в соответствии с минимальным стандартом компетентности
для капитанов и старших помощников капитана (в соответствии с ПДНВ)
Понимание основных принципов устройства судна, теорий и факторов, влияющих на посадку и остойчивость, а также мер, необходимых для обеспечения безопасной посадки и остойчивости
Слайд 6 Остойчивостью называется способность плавающего судна, выведенного из положения равновесия воздействием внешних
сил, вновь возвращаться в первоначальное положение после прекращения действия этих сил
Слайд 8 Начальная остойчивость – это остойчивость судна по отношению к бесконечно малым
отклонениям от положений равновесия
Остойчивость
Начальная остойчивость
Остойчивость на больших
наклонениях
Слайд 9Признак начальной остойчивости
Судно остойчиво, если после любого произвольного бесконечно малого отклонения,
изменяющего его посадку, будучи предоставленным самому себе, оно возвращается в исходное положение равновесия
Слайд 10Произвольное отклонение складывается из составляющих:
- Вертикальное отклонение
Горизонтальные отклонения
Угловые отклонения (крен и/или
дифферент)
Угловые отклонения в вертикальной плоскости называют наклонениями судна (поперечными и продольными)
Угловые отклонения в вертикальной плоскости называют наклонениями судна (поперечными и продольными)
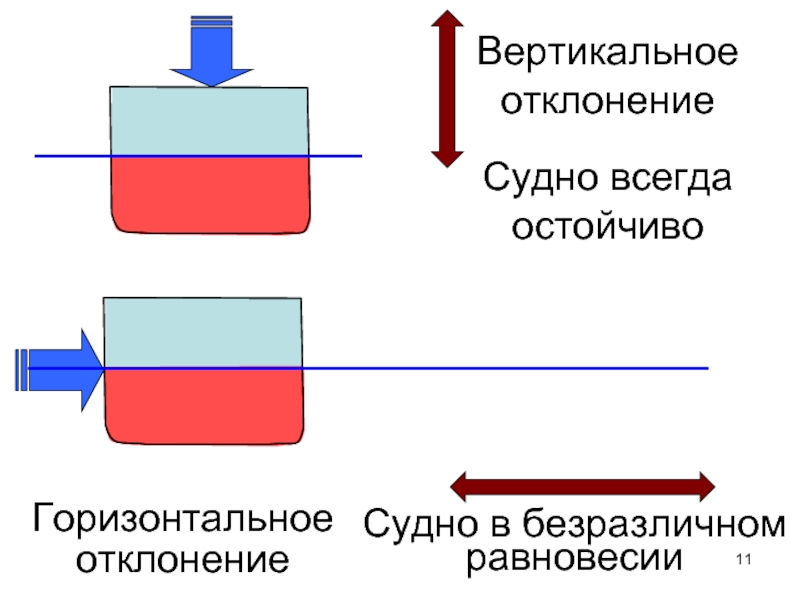
Слайд 11
Судно всегда остойчиво
Судно в безразличном равновесии
Вертикальное отклонение
Горизонтальное
отклонение
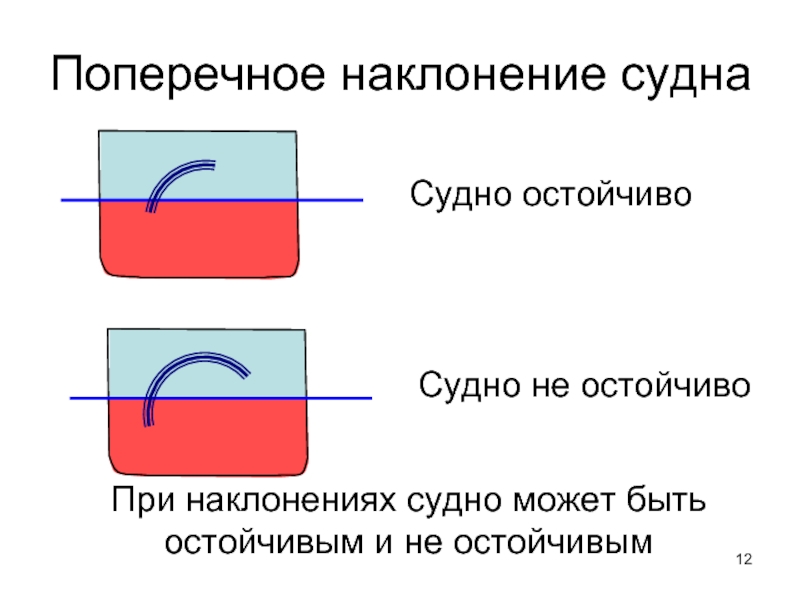
Слайд 12Поперечное наклонение судна
Судно остойчиво
Судно не остойчиво
При наклонениях судно может быть
остойчивым и не остойчивым
Слайд 13Признак остойчивости равновесия судна
Судно остойчиво, если оно остойчиво на всех возможных
наклонениях
Слайд 14Определения
- Ось наклонения – это линия пересечения исходной и конечной ватерлиний
при наклонениях
- Плоскость наклонения –плоскость, перпендикулярная оси наклонения и проходящая через центр величины судна при исходной посадке
- Угол наклонения – это угол между исходной и конечной ватерлиниями
- Плоскость наклонения –плоскость, перпендикулярная оси наклонения и проходящая через центр величины судна при исходной посадке
- Угол наклонения – это угол между исходной и конечной ватерлиниями
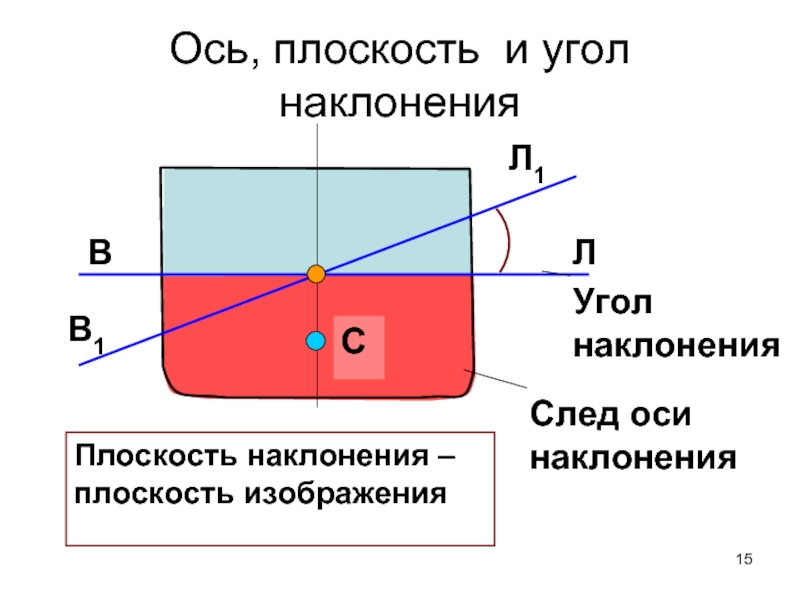
Слайд 15Ось, плоскость и угол наклонения
След оси
наклонения
Угол наклонения
В1
Л1
Плоскость наклонения – плоскость изображения
C
Слайд 17Равнообъемные наклонения
При равнообъемных наклонениях величина погруженного объема судна остается постоянной
Произвольное наклонение
судна можно представить, как:
Равнообъемное наклонение
Вертикально-поступательное перемещение
Равнообъемное наклонение
Вертикально-поступательное перемещение
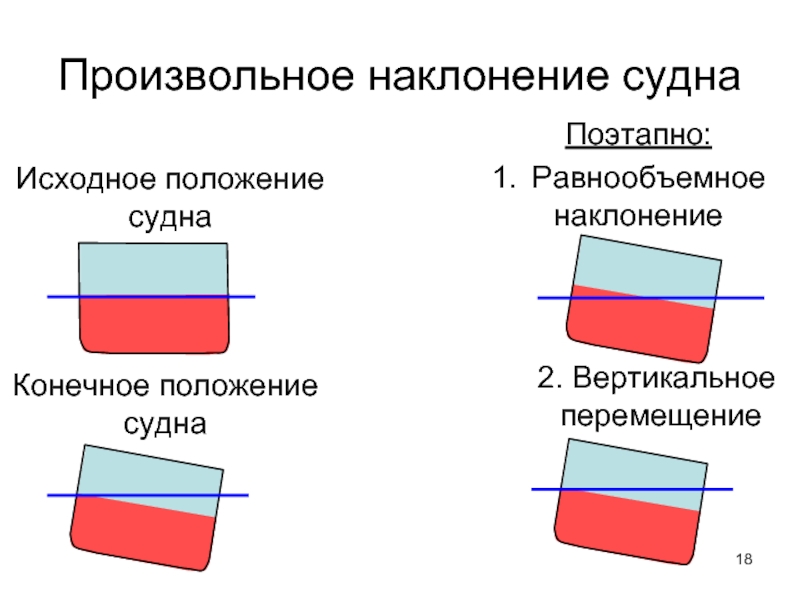
Слайд 18Произвольное наклонение судна
Равнообъемное
наклонение
2. Вертикальное
перемещение
Исходное положение
судна
Конечное положение
судна
Поэтапно:
Слайд 19Признак остойчивости судна
Судно является остойчивым, если оно остойчиво по отношению к
любым возможным бесконечно малым равнообъемным наклонениям из данного положения равновесия
В дальнейшем рассматриваем только поперечные и продольные наклонения с углами крена θ и дифферента ψ
В дальнейшем рассматриваем только поперечные и продольные наклонения с углами крена θ и дифферента ψ
Слайд 20Выдающийся ученый, математик, механик и астроном, один из основателей науки «теория
корабля»
В 1731-41 и с 1766
академик Санкт-Петербургской Академии Наук
Леонард Эйлер
(1707-83)
Слайд 22Теорема Эйлера о равнообъемных наклонениях:
- Бесконечно близкие равнообъемные ватерлинии пересекаются по оси,
проходящей через их общий центр тяжести
- Ось бесконечно малого равнообъемного наклонения проходит через центр тяжести площади ватерлинии
- Ось бесконечно малого равнообъемного наклонения проходит через центр тяжести площади ватерлинии
Слайд 23Использование теоремы Эйлера
Теорема Эйлера применима и для небольших конечных наклонений
Теорема Эйлера
используется в практических задачах уточнения посадки и определения ЭПО судна, сидящего с дифферентом
Слайд 25Уточненное определение объемного водоизмещения V при посадке судна с небольшим дифферентом:
В
грузовой размер V(d) войти с осадкой df = d + xf ψ
Определить V, соответствующую посадке без дифферента с осадкой df
По теореме Эйлера она равна V судна, сидящего с дифферентом с осадкой d на миделе
Определить V, соответствующую посадке без дифферента с осадкой df
По теореме Эйлера она равна V судна, сидящего с дифферентом с осадкой d на миделе
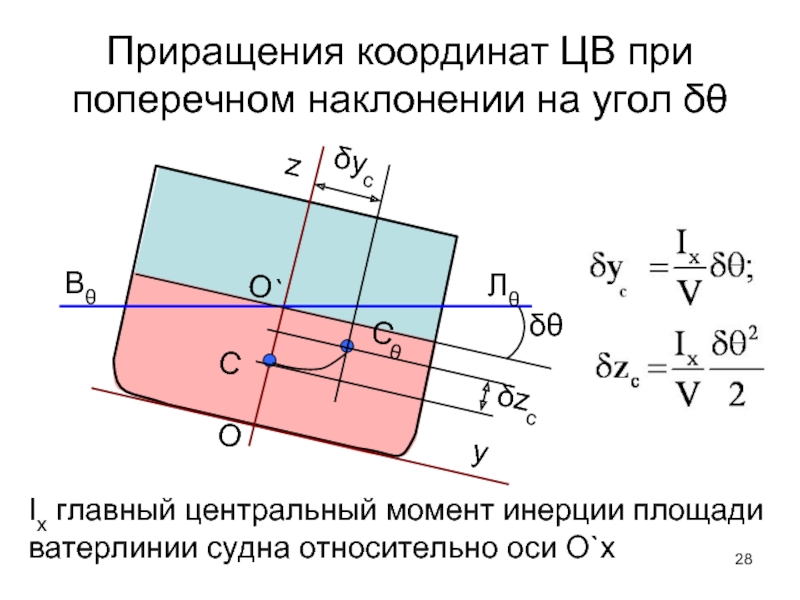
Слайд 28Приращения координат ЦВ при поперечном наклонении на угол δθ
δzc
δyc
δθ
Ix главный центральный
момент инерции площади ватерлинии судна относительно оси O`x
Слайд 29Приращения координат ЦВ при продольном наклонении на угол δψ
Вψ
Лψ
Iyf - главный
центральный момент инерции площади ватерлинии судна относительно оси Fy
Слайд 30Приращения координат ЦВ
Моменты инерции характеризуют распределение площади ватерлинии относительно осей O`x
и Fy
Ix и Iyf – величины положительные
Знаки δyc и δxc совпадают со знаками δθ и δψ соответственно
δzc всегда положительно
Ix и Iyf – величины положительные
Знаки δyc и δxc совпадают со знаками δθ и δψ соответственно
δzc всегда положительно
Слайд 31Уточнение xc судна, сидящего с дифферентом по кривым элементов ТЧ (гидростатическим
кривым)
По кривой xc(d) найти xc при осадке d
По кривой R(d) найти R при осадке d
Вычислить xcψ = xc + R tgψ ≈ xc + R ψ
Слайд 32«Кривая С»
При равнообъемных наклонениях ЦВ судна всегда смещается в сторону наклонения
и вверх по отношению к своему исходному положению
2. «Кривая С» - это плоская кривая линия, по которой перемещается ЦВ судна при равнообъемных наклонениях в одной плоскости
2. «Кривая С» - это плоская кривая линия, по которой перемещается ЦВ судна при равнообъемных наклонениях в одной плоскости
Слайд 33Перемещения силы плавучести при наклонениях
Сила плавучести приложена в ЦВ судна, следовательно,
при наклонениях точка ее приложения перемещается в соответствии с описанными выше перемещениями ЦВ
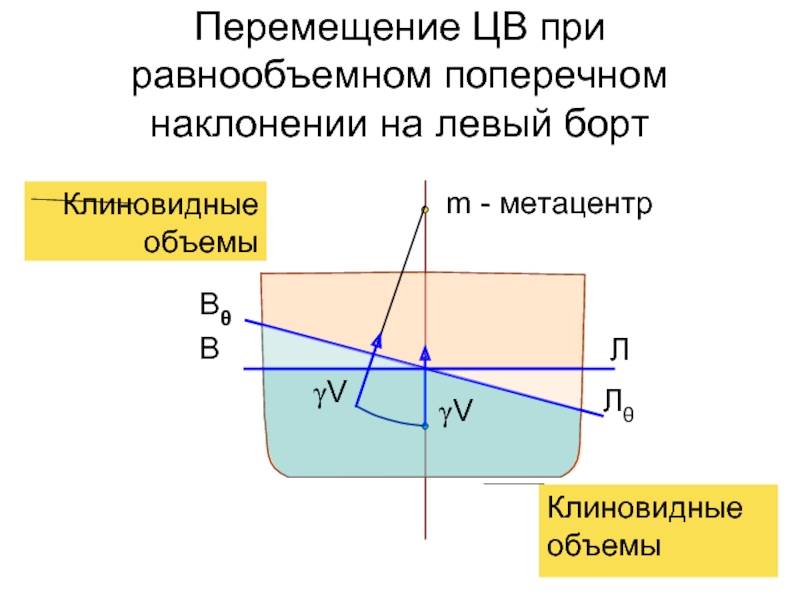
Слайд 34Перемещение ЦВ при равнообъемном поперечном наклонении на левый борт
m - метацентр
γV
Клиновидные объемы
γV
Клиновидные объемы
В
Л
