- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Напряженное состояние в грунтах. (Лекция 5) презентация
Содержание
- 1. Напряженное состояние в грунтах. (Лекция 5)
- 3. Распределение напряжений в
- 4. Характер распределения напряжений Два направления изучения напряженного
- 5. Отличия грунтов основания
- 6. Работа оснований сооружений в зависимости от принятой
- 7. Д о п у
- 8. 1 - основание в допредельном состоянии, 2-
- 9. I фаза - упругих деформаций
- 10. II фаза –
- 11. III фаза – интенсивных сдвигов (участок III) Ркр.нач.≤ Р
- 12. Давление, соответствующее началу появления областей
- 13. IVфаза – выпирания Р ≥ Р кр.пред.
- 14. С помощью теории упругости можно только определить
- 15. 5.3 Расчетные модели грунтовых оснований
- 16. Модель Фусса-Винклера Коэффициент пропорциональности между нагрузкой и деформацией называется коэффици-ентом постели.
- 17. Модель линейно-деформируемого
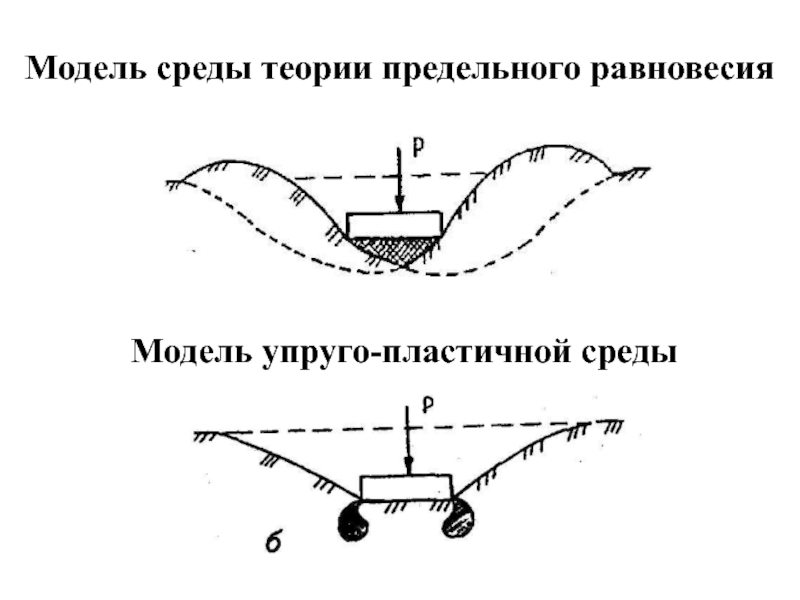
- 18. Модель среды теории предельного равновесия Модель упруго-пластичной среды
- 19. σz σу σх τух τху τzx τxz
- 20. Схема к определению напряжений при действии сосредоточенной
- 21. Схема распределения напряжений по полушаровой поверхности с
- 22. При одном и том
- 23. (1) где а -
- 24. Подставив в формулу (1)
- 25. Вертикальные нормальные напряжения
- 26. (7)
- 27. обозначив формула примет вид:
- 28. Перемещения, параллельные осям координат:
- 29. Р1 =Р2=Р3, R1 < R2 < R3,
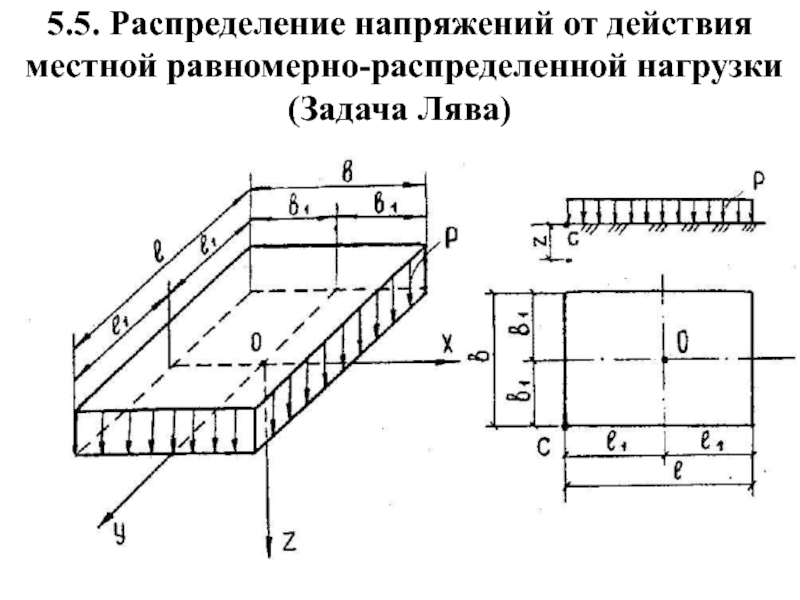
- 30. 5.5. Распределение напряжений от действия местной равномерно-распределенной нагрузки (Задача Лява)
- 31. Для точек, расположенных на вертикали,
- 32. Сжимающие напряжения, возникающие
- 33. Напряжение под угловыми точками
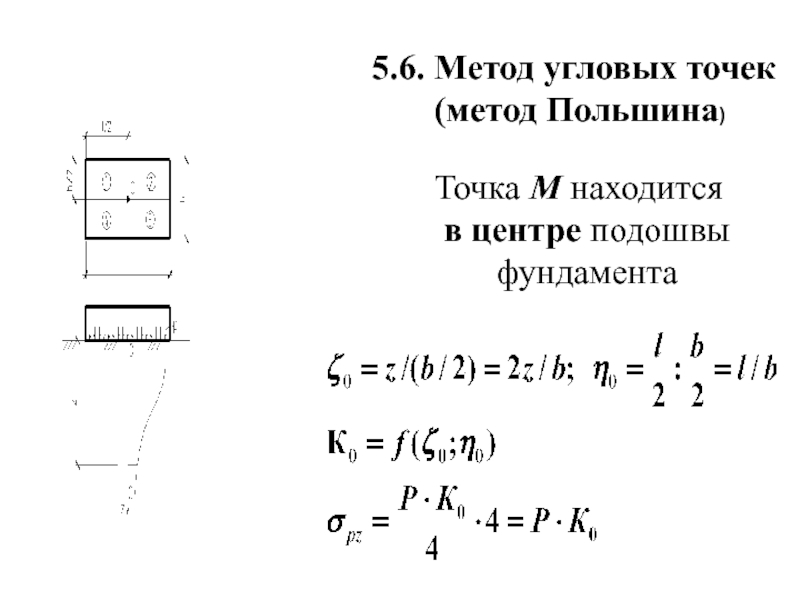
- 34. 5.6. Метод угловых точек
- 35. Точка М находится внутри прямоугольника и не проходит через его центр;
- 36. Точка М расположена за пределами контура прямоугольника загружения
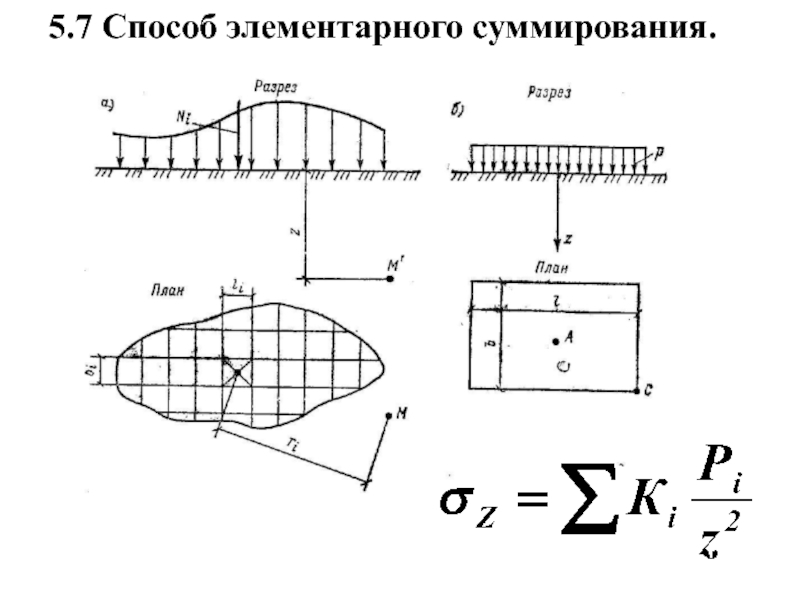
- 37. 5.7 Способ элементарного суммирования.
Слайд 2
Слайд 3 Распределение напряжений в грунтовой толще зависит от
- характера и режима нагружения массива;
- инженерно-геологических и гидрогеологи-ческих особенностей площадки строительства;
- состава и физико-механических свойств грунтов.
5.1. Основы напряженного состояния
грунтов оснований
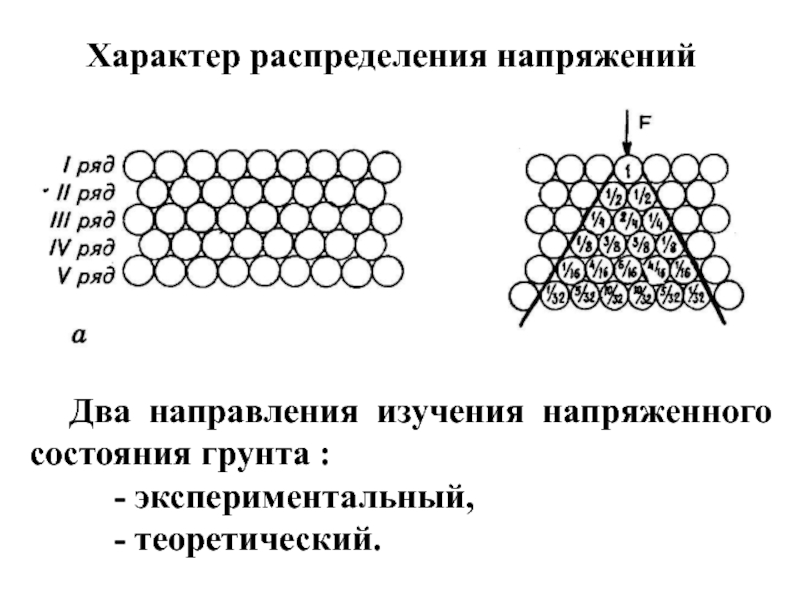
Слайд 4Характер распределения напряжений
Два направления изучения напряженного состояния грунта :
- теоретический.
Слайд 5 Отличия грунтов основания от материалов
строительных конструкций:
малая прочность и большая деформируемость;
деформация во времени при постоянной нагрузке
возрастает;
неоднородность грунтов и их свойств в основании
фундаментов;
неоднородность напряжений в грунтовой толще в
естественных условиях и сложность их измерений
под действием внешней нагрузки;
различие закономерностей изменения напряжен-
ного состояния грунтов, однородных по составу,
но при различной величине внешней нагрузки.
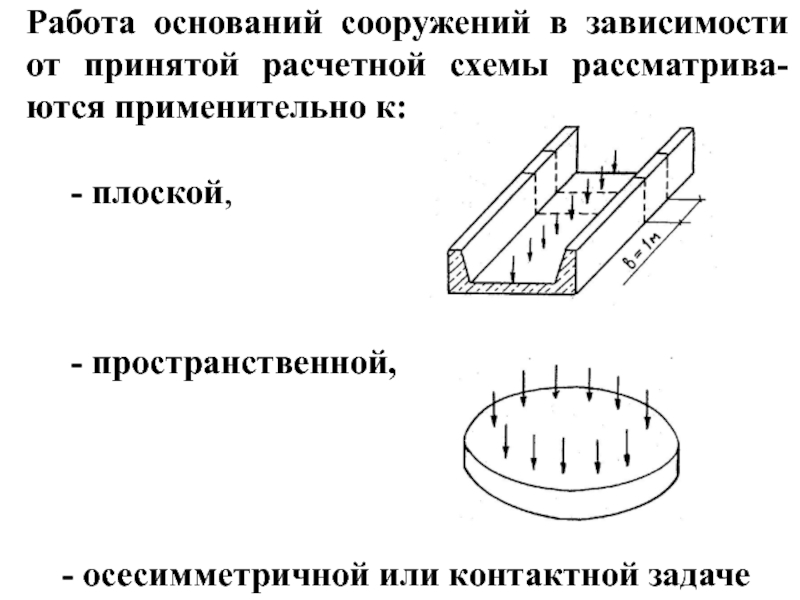
Слайд 6Работа оснований сооружений в зависимости от принятой расчетной схемы рассматрива-ются применительно
- плоской,
- пространственной,
- осесимметричной или контактной задаче
Слайд 7 Д о п у щ е н и
1. Давление на грунт не превышает вели-чины начального критического Р ≤ Р кр.нач.
2. Грунт нагружается только один раз.
3. Грунт является сплошным телом.
4. Грунт является изотропным телом.
5.2. Фазы напряженного состояния грунта.
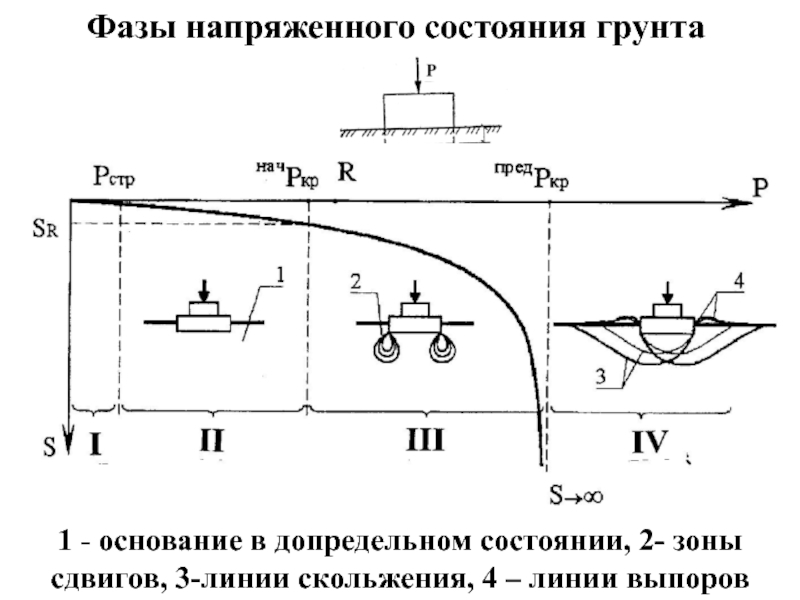
Слайд 81 - основание в допредельном состоянии, 2- зоны сдвигов, 3-линии скольжения,
Фазы напряженного состояния грунта
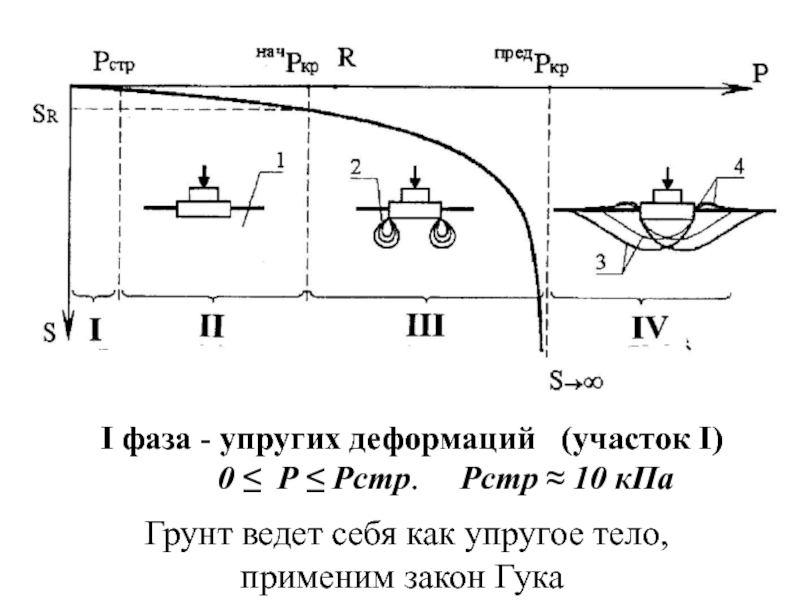
Слайд 9 I фаза - упругих деформаций (участок I)
0 ≤ Р ≤ Рстр. Рстр ≈ 10 кПа
Грунт ведет себя как упругое тело,
применим закон Гука
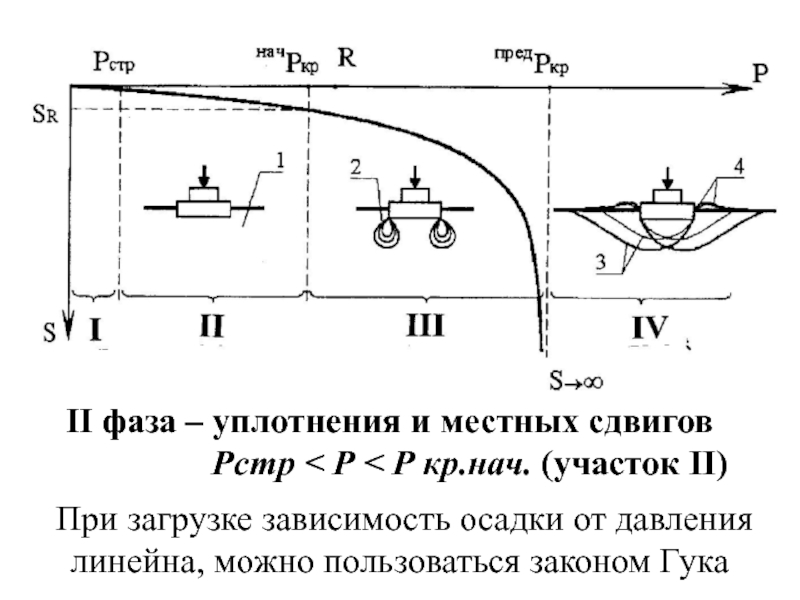
Слайд 10 II фаза – уплотнения и местных сдвигов
Рстр < Р < Р кр.нач. (участок II)
При загрузке зависимость осадки от давления линейна, можно пользоваться законом Гука
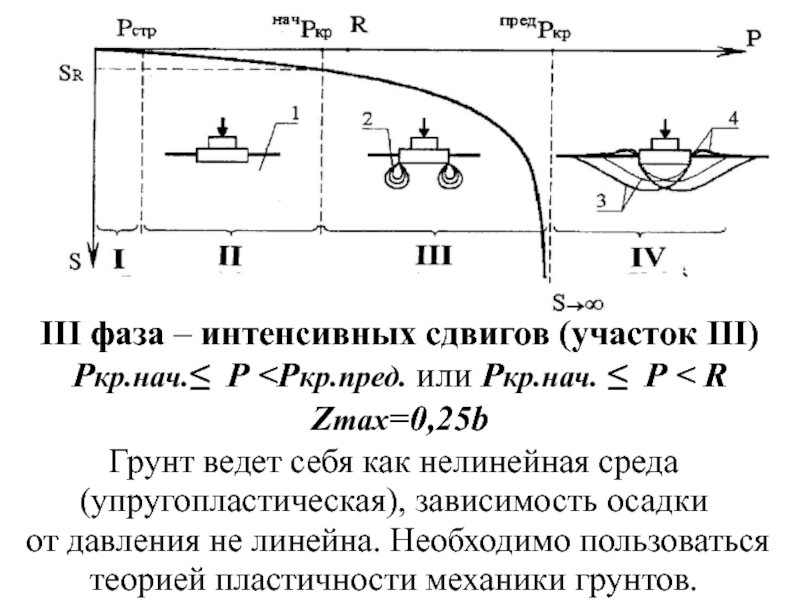
Слайд 11III фаза – интенсивных сдвигов (участок III)
Ркр.нач.≤ Р
Грунт ведет себя как нелинейная среда (упругопластическая), зависимость осадки
от давления не линейна. Необходимо пользоваться теорией пластичности механики грунтов.
Слайд 12 Давление, соответствующее началу появления областей пластических деформаций (сдвигов
Давление, соответствующее исчерпанию несущей способности грунта основания, назы-вается предельным критическим давлением, Р кр. пред.
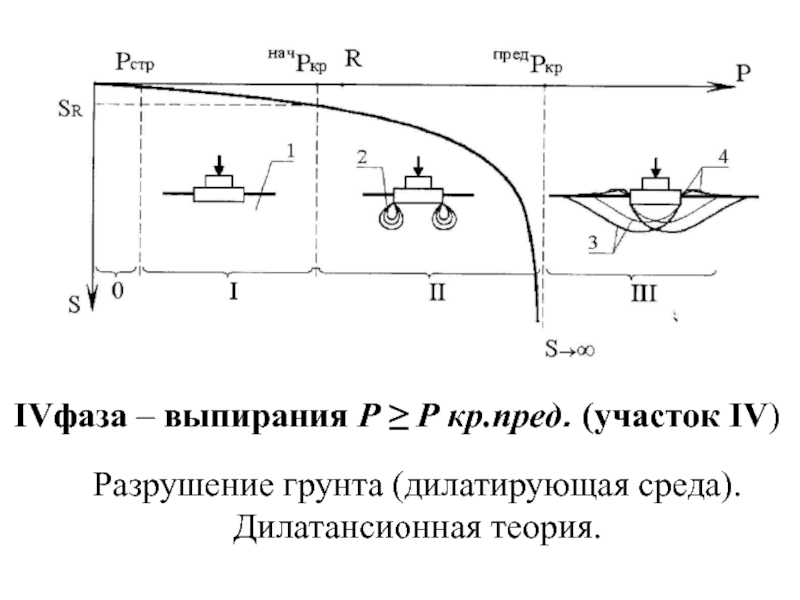
Слайд 13IVфаза – выпирания Р ≥ Р кр.пред. (участок IV)
Разрушение грунта
Слайд 14С помощью теории упругости можно только определить конечную осадку при Р
Несоблюдение этого условия может привести
к значительным ошибкам в расчетах.
Осадки во времени определяют с помощью теории фильтрационной консолидации.
Слайд 155.3 Расчетные модели грунтовых оснований
Две группы:
- линейные модели, в которых зависимость между напряжениями и деформациями является линейной;
- нелинейные, в которых эта зависимость является нелинейной
Слайд 16Модель Фусса-Винклера
Коэффициент пропорциональности между нагрузкой и деформацией
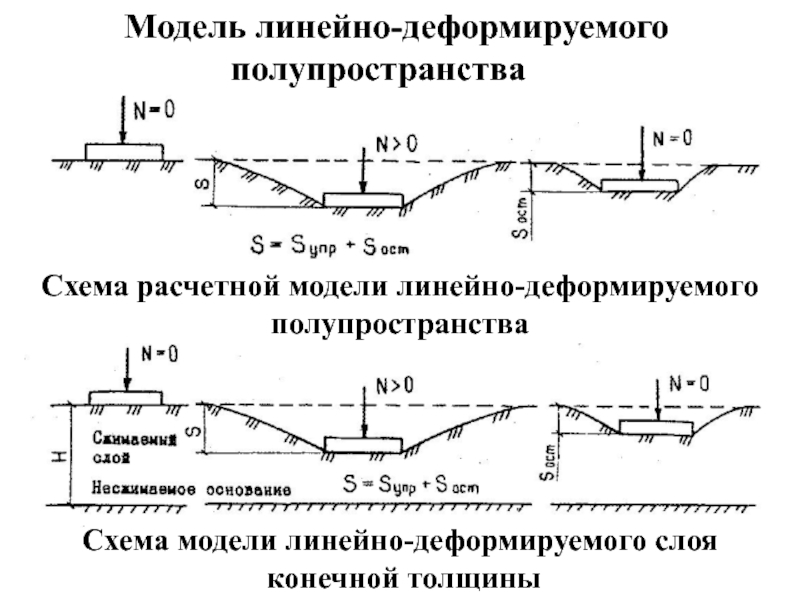
Слайд 17Модель линейно-деформируемого
полупространства
Схема расчетной модели линейно-деформируемого
Схема модели линейно-деформируемого слоя
конечной толщины
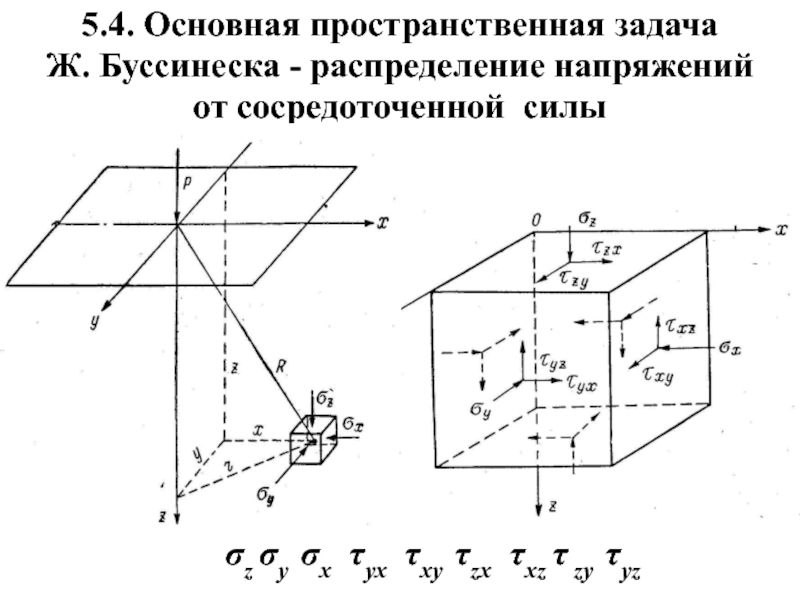
Слайд 19σz σу σх τух τху τzx τxz τ zy τyz
5.4. Основная
Ж. Буссинеска - распределение напряжений
от сосредоточенной силы
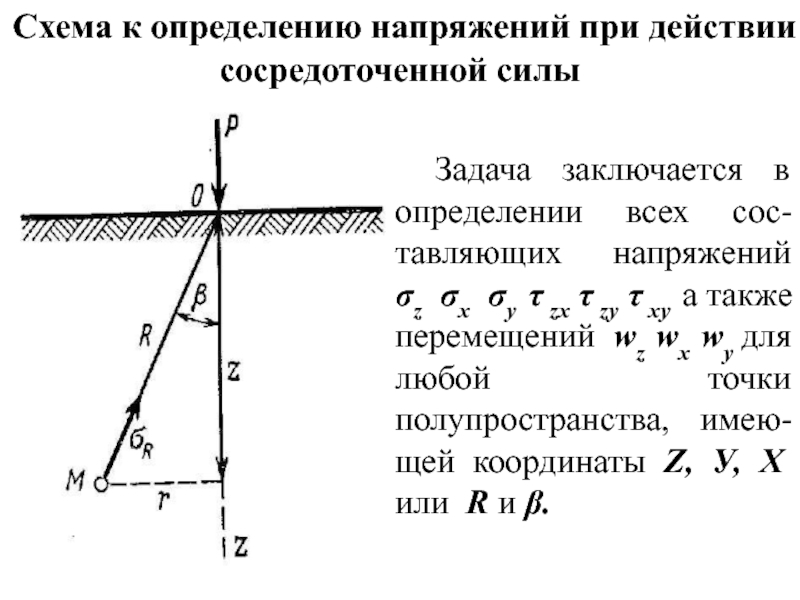
Слайд 20Схема к определению напряжений при действии сосредоточенной силы
Задача заключается в
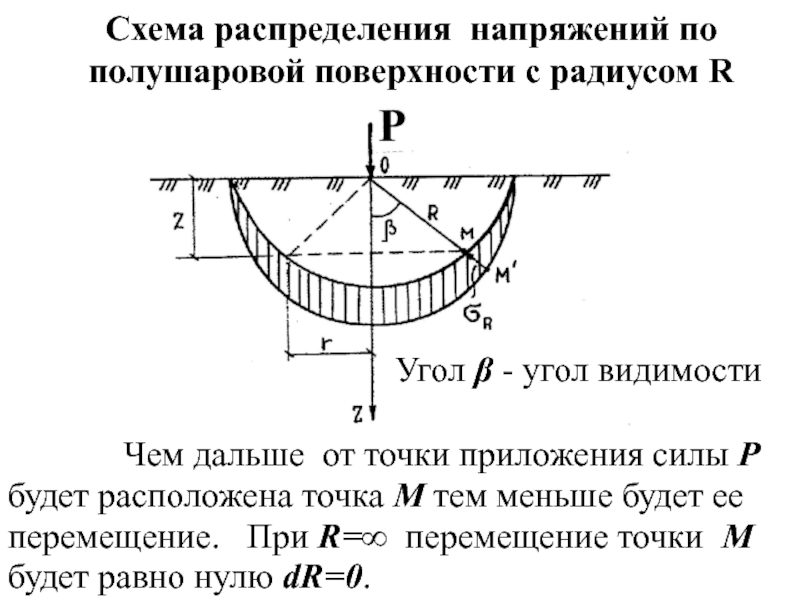
Слайд 21Схема распределения напряжений по полушаровой поверхности с радиусом R
Угол β - угол видимости
Слайд 22 При одном и том же значении R для
Наибольшее перемещение получит точка, рас-положенная по оси z, т.е. β=0.
С увеличением угла β перемещения по направ-лению радиуса R уменьшаются, и в случае β=900 (на поверхности грунта) при малых деформациях будут равны нулю.
В точке приложения силы, где R=0 следует σz =∞.
Слайд 23
(1)
где а - коэффициент, определяемый из условия
радиальных напряжений при действии сосредо-
точенной силы
Р-ΣσR=0
Приняв как постулат, что σR прямо пропорцио- нально cosβ и обратно R2, можно записать зависи-мость
Тогда можно записать
(2)
Слайд 24 Подставив в формулу (1) а, получим формулу Буссинеска
(3)
Слайд 27обозначив
формула примет вид:
где К – коэффициент
определяется для ряда значений r/z
r – расстояние по горизонтали от оси Z,
проходящей через точку приложения
сосредоточенной силы
z – глубина рассматриваемой точки.
(9)
(10)
Слайд 29Р1 =Р2=Р3, R1 < R2 < R3, r1σz3
К -
по таблице (или формуле)
Напряжения от действия группы сил
Слайд 305.5. Распределение напряжений от действия
местной равномерно-распределенной нагрузки
(Задача Лява)
Слайд 31
Для точек, расположенных на вертикали, проходящей через центр загруженной площади, формула
Для точек, расположенных на глубине на прямых, проходящих через углы загружаемой площади, угло-вое напряжение определяется по формуле:
Слайд 32 Сжимающие напряжения, возникающие под центром О прямоугольной
σ z =К⋅ р
где К – коэффициент, принимаемый по табл.СНиП
как функции относительной глубины β=2z/b
или β=z/b и соотношению сторон прямо-
угольной площади загрузки α=l/b принимают
в зависимости от величин
К=f(2z / b, l / b) η = l / b и ζ = 2z / b
где l – длинная сторона прямоугольной площади
загружения; b - ее ширина.
р - равномерно-распределенное давление.
Слайд 33 Напряжение под угловыми точками определяют по формуле:
σ z
К - коэффициент рассеивания напряжений для угловых точек, определяются по таблицам СНиП или любого учебника в зависимости от величин
η = l / b и ζ = z / b.
Формула σz =0,25К⋅р – используется для
определения влияния фундаментов друг на друга.