Русакова Н.П.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моменты импульса (угловые моменты). Часть первая презентация
Содержание
- 1. Моменты импульса (угловые моменты). Часть первая
- 2. Лекция № 6 2 Атом в квантовой
- 3. Лекция № 6 3 Классическое определение: Моме́нт
- 4. Чтобы определить количество движения (момент импульса) ē
- 5. Лекция № 6 5 Скорость движения ē по орбите:
- 6. Лекция № 6 6 Размер атома (Боровский радиус)
- 7. Лекция № 6 7 Момент импульса: Классическое
- 8. Лекция № 6 8 Момент импульса: Может
- 9. Лекция № 6 9 Одновременное значение только
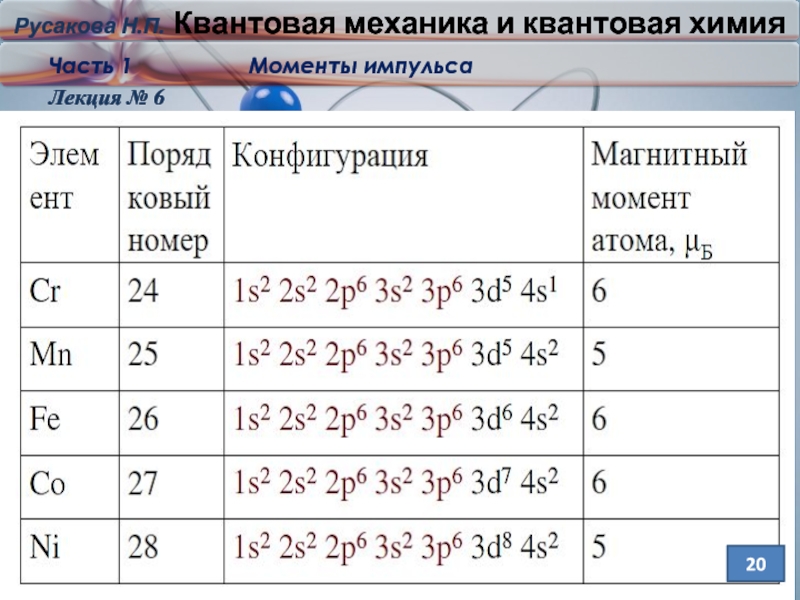
- 10. Лекция № 6 10
- 11. Лекция № 6 11 S = πR2
- 12. Лекция № 6 12
- 13. Лекция № 6 13 Cпин 1925- Гаудсмит
- 14. Лекция № 6 14 Собственному механическому моменту
- 15. Лекция № 6 2 Состояние электрона в
- 16. Лекция № 6 19
- 17. Лекция № 6 16
- 18. Лекция № 6 17
- 19. Лекция № 6 18
- 20. Лекция № 6 20
- 21. Лекция № 6 21 Спасибо за внимание!
- 22. Задание на усвоение Что представляет собой механический
Слайд 2Лекция № 6
2
Атом в квантовой механике
Атом водорода в
квантовой механике:
Движение
двух заряженных частиц (ē в поле ядра):
Масса ядра » массы ē. Ядро – неподвижно. Вращательное движение ē, зависящее от ē массы, её распределения по объёму атома и скорости её вращения.
А это –
МОМЕНТ ИМПУЛЬСА ē
Масса ядра » массы ē. Ядро – неподвижно. Вращательное движение ē, зависящее от ē массы, её распределения по объёму атома и скорости её вращения.
А это –
МОМЕНТ ИМПУЛЬСА ē
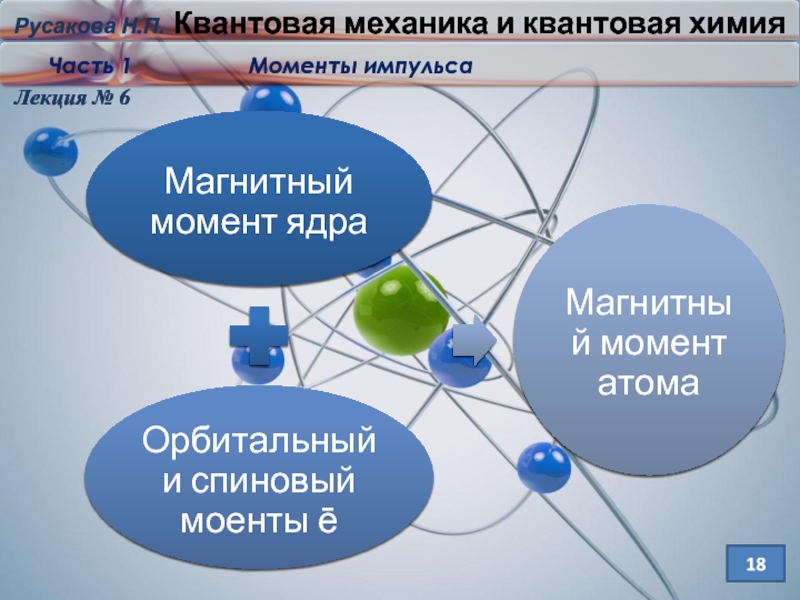
Механический момент атома
I= L+S
Слайд 3Лекция № 6
3
Классическое определение:
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент,
момент количества движения) характеризует количество вращатель-ного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение
Момент импульса L материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
(https://ru.wikipedia.org )
Момент импульса L материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
(https://ru.wikipedia.org )
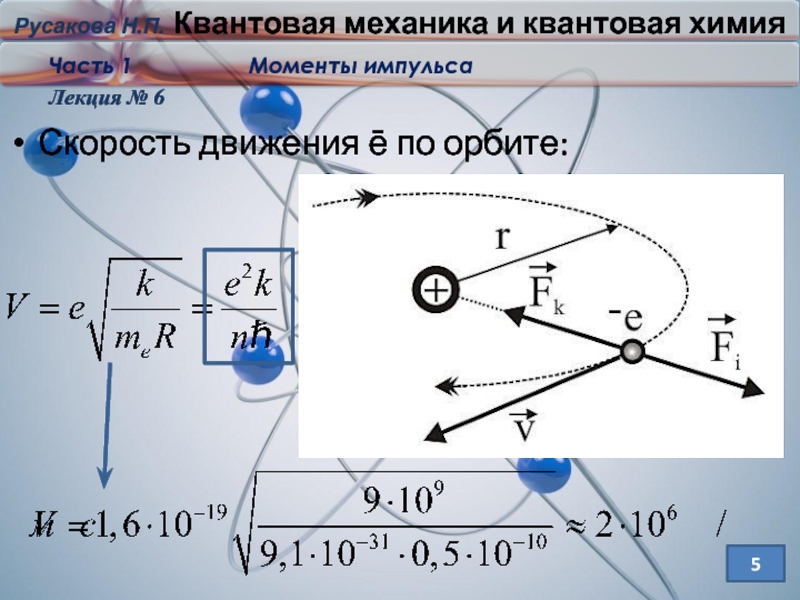
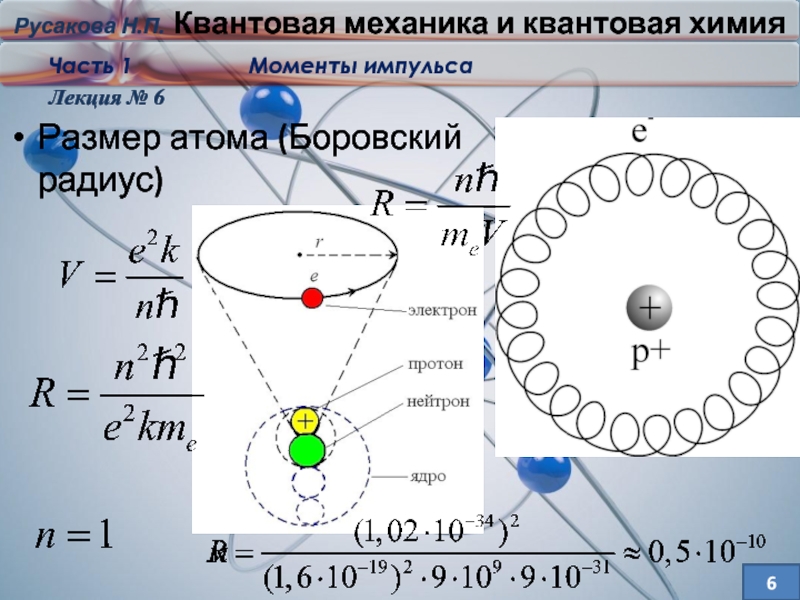
Слайд 4Чтобы определить количество движения (момент импульса) ē необходимо знать:
Размер атома (Боровский
радиус -радиус ближайшей к ядру орбиты электрона атома водорода).
= 5,2917720859(36)·10−11 м
α - Постоя́нная то́нкой структу́ры является фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия
Скорость движения ē по ор- бите атома
= 5,2917720859(36)·10−11 м
α - Постоя́нная то́нкой структу́ры является фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия
Скорость движения ē по ор- бите атома
Лекция № 6
4
Слайд 7Лекция № 6
7
Момент импульса:
Классическое пон.:
Проекция импульса ē на ось Z –
(и любое другое выделенное направление) не зависит от времени
Слайд 8Лекция № 6
8
Момент импульса:
Может принимать только значения пропорциональные целому числу :
Квантование
момента импульса:
В кв. мех. Каждой физ. величине а сопоставляется оператор Â.
Для момента импульса в кв. мех вводятся четыре оператора:
Одновременное значение могут иметь: и одна из проекций оператора импульса на оси. Две остальные остаются неопределёнными
В кв. мех. Каждой физ. величине а сопоставляется оператор Â.
Для момента импульса в кв. мех вводятся четыре оператора:
Одновременное значение могут иметь: и одна из проекций оператора импульса на оси. Две остальные остаются неопределёнными
Слайд 9Лекция № 6
9
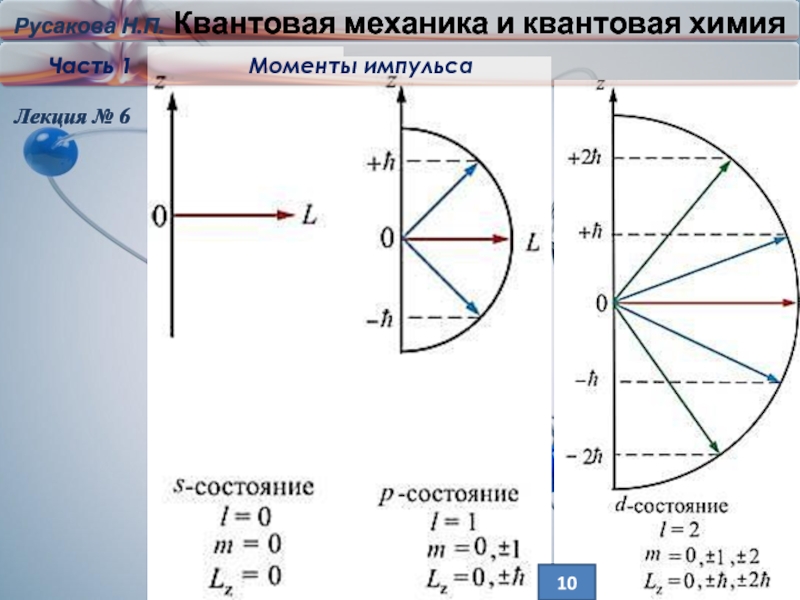
Одновременное значение только двух операторов момента импульса означает, что
вектор момента не имеет определённого направления и не может быть изображён (как в классической мех.).
Решением уравнения: ψ=L2ψ
будут собственные значения оператора :
L=ћ
l=0,1,…,n-1 l- орбитальное (азимутальное) квантовое число
Решением уравнения: ψ=L2ψ
будут собственные значения оператора :
L=ћ
l=0,1,…,n-1 l- орбитальное (азимутальное) квантовое число
Слайд 13Лекция № 6
13
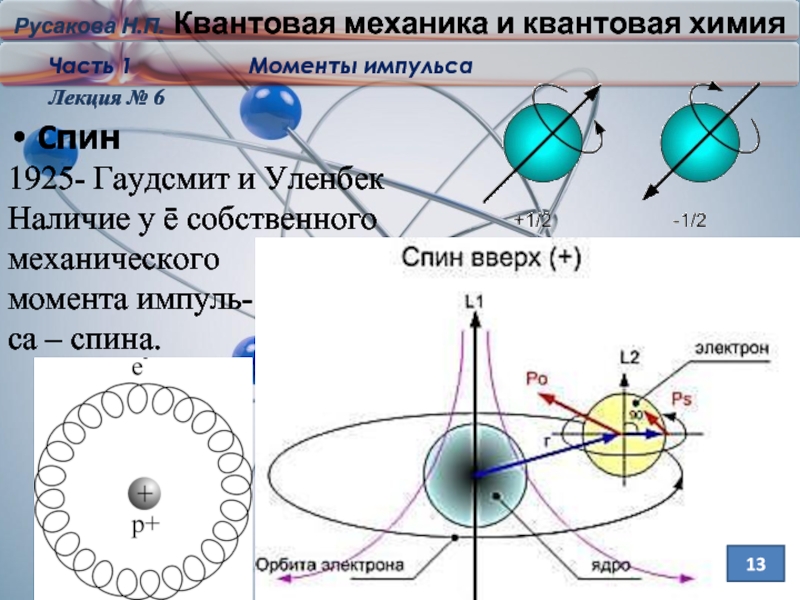
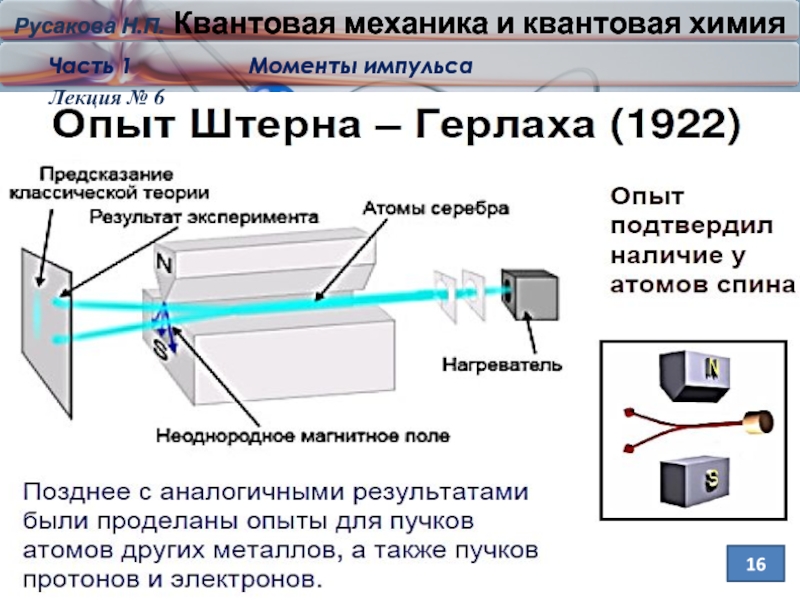
Cпин
1925- Гаудсмит и Уленбек
Наличие у ē собственного
механического
момента импуль-
са – спина.
Слайд 14Лекция № 6
14
Собственному механическому моменту импульса соответству-ет собственный магнитный мо-мент. Проекция
собственного магнитного момента на
выделенное
направление
составляет ± ћ.
неверное представление
направление
составляет ± ћ.
неверное представление
Слайд 15Лекция № 6
2
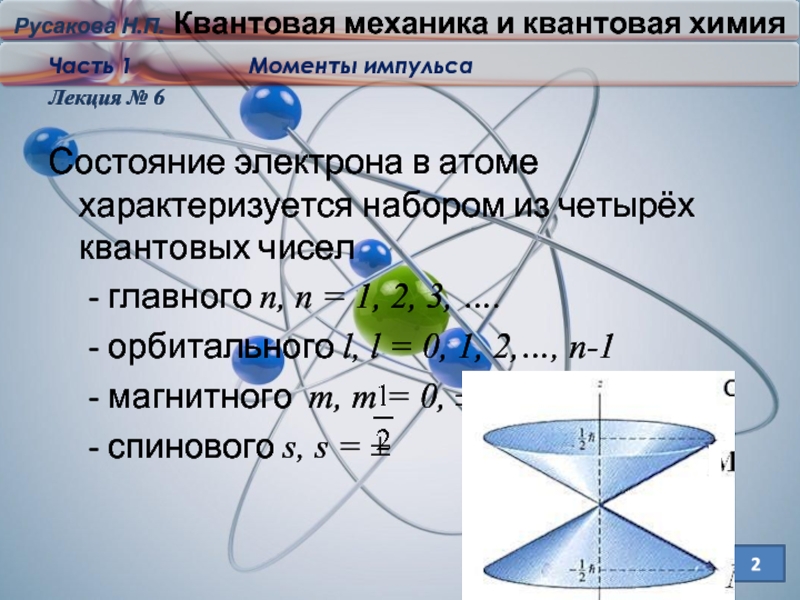
Состояние электрона в атоме характеризуется набором из четырёх квантовых
чисел
- главного n, n = 1, 2, 3, ….
- орбитального l, l = 0, 1, 2,…, n-1
- магнитного m, m = 0, ±1, ±2, …., ±l
- спинового s, s = ±
- главного n, n = 1, 2, 3, ….
- орбитального l, l = 0, 1, 2,…, n-1
- магнитного m, m = 0, ±1, ±2, …., ±l
- спинового s, s = ±
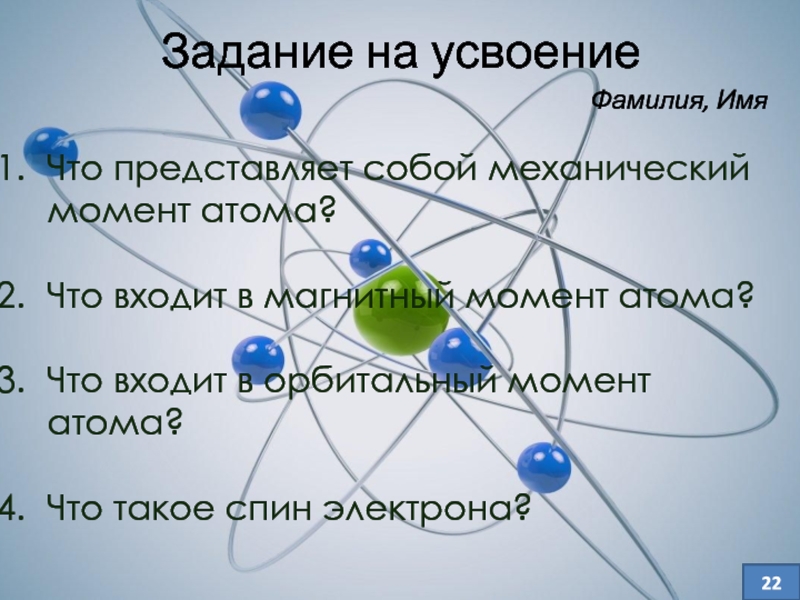
Слайд 22Задание на усвоение
Что представляет собой механический момент атома?
Что входит в магнитный
момент атома?
Что входит в орбитальный момент атома?
Что такое спин электрона?
Что входит в орбитальный момент атома?
Что такое спин электрона?
Фамилия, Имя
22