- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
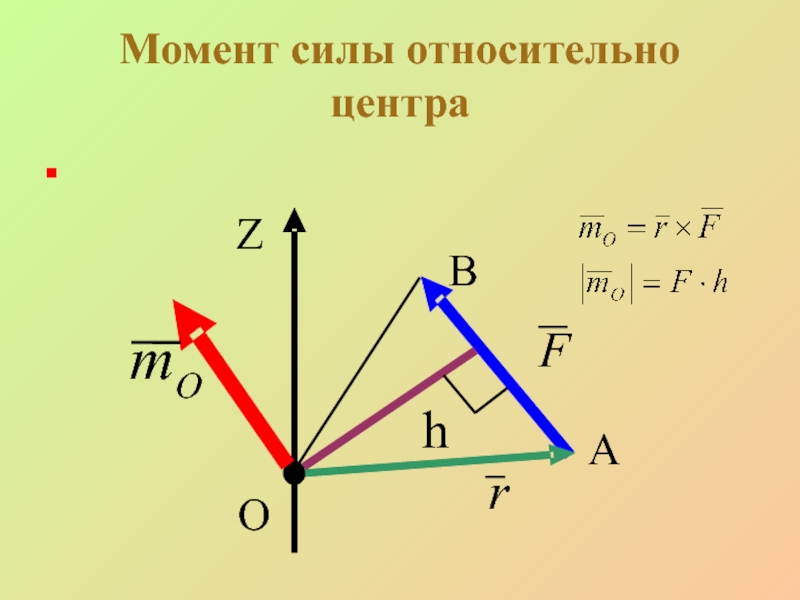
Момент силы относительно центра (точки) презентация
Содержание
- 1. Момент силы относительно центра (точки)
- 2. 2.1 Момент силы относительно центра (точки)
- 3. Момент силы относительно центра
- 5. Свойства момента силы:
- 6. О
- 8. Пьер Вариньон Пьер Вариньон (фр. Pierre Varignon,
- 9. Теорема Вариньона
- 10. 2.2 Теория пар сил, свойства пар сил
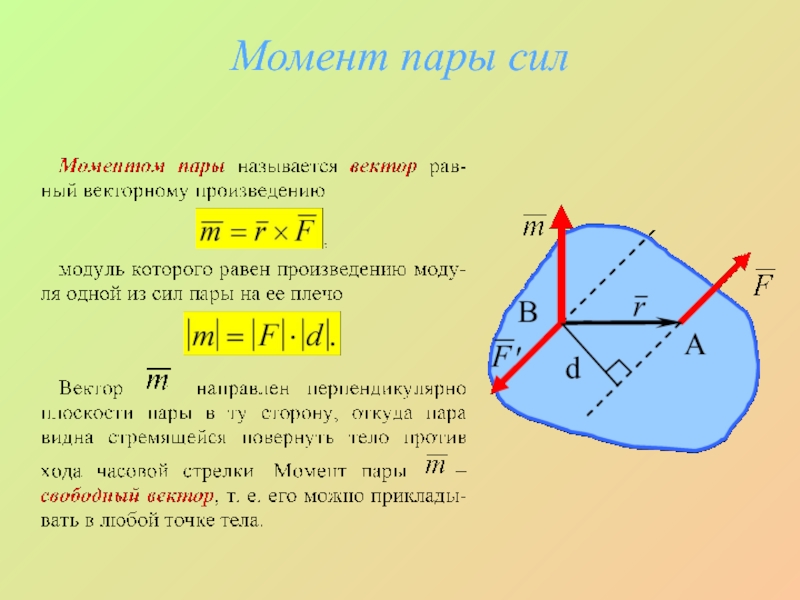
- 11. Момент пары сил
- 12. Свойства пар сил
- 16. 2.3 Приведение системы сил к заданному центру Теорема Пуансо
- 17. Пуансо Луи Пуансо (Poinsot) Луи (3.1.1777,
- 18. Теорема1 - О параллельном переносе силы
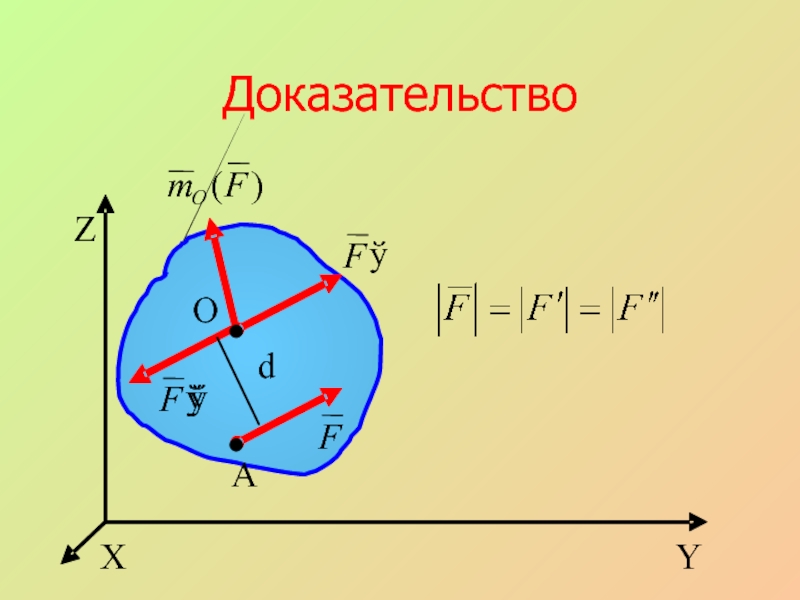
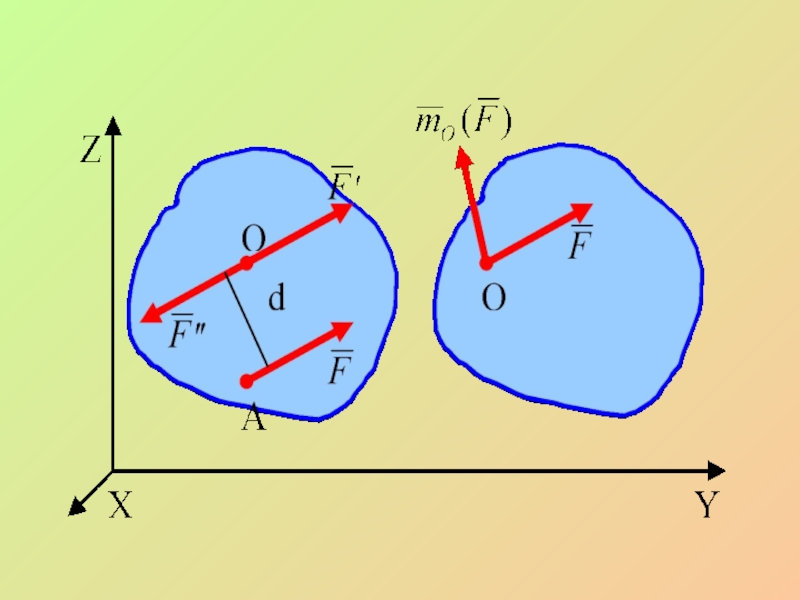
- 19. Доказательство
- 21. Теорема 2 – О приведении системы сил
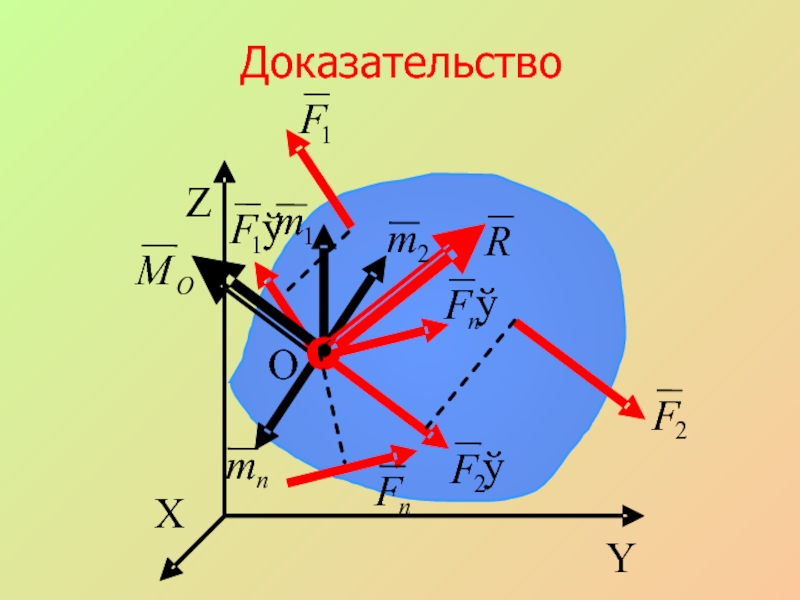
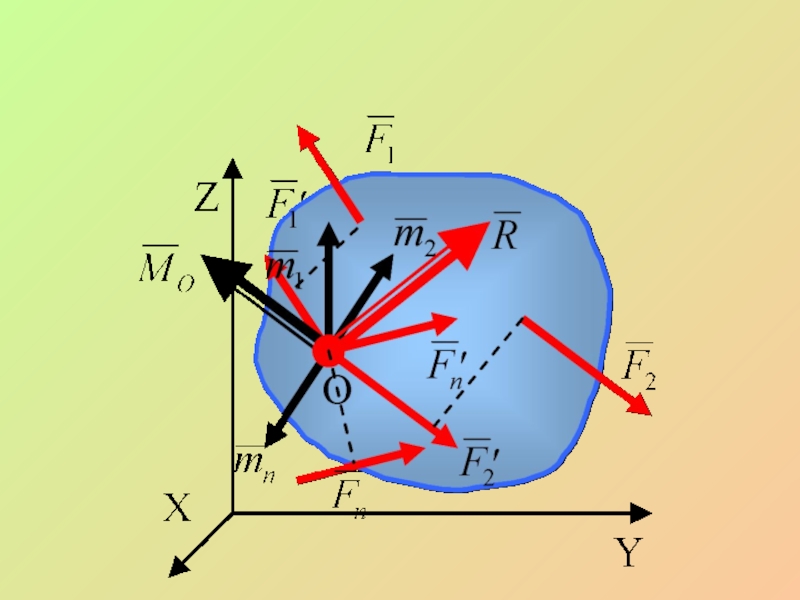
- 22. Доказательство
- 24. Используя теорему 1 перенесем все силы в
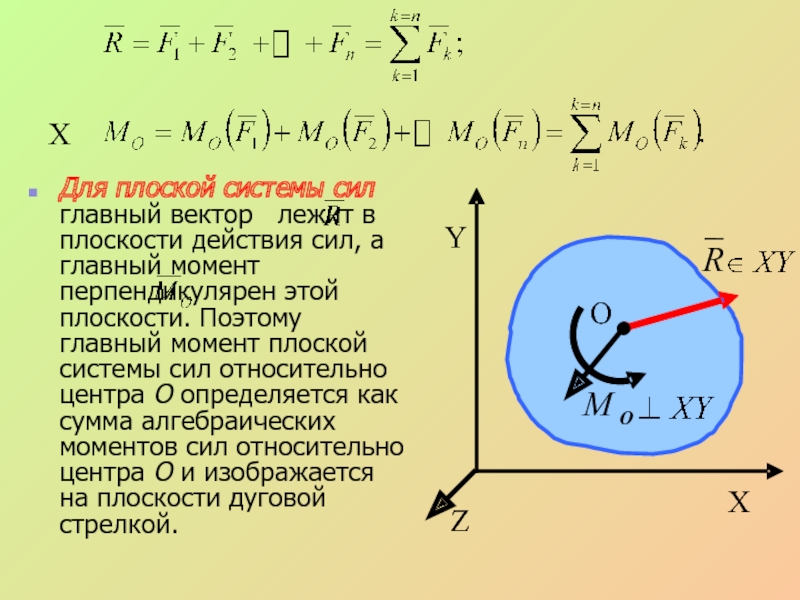
- 25. Для плоской системы сил главный вектор
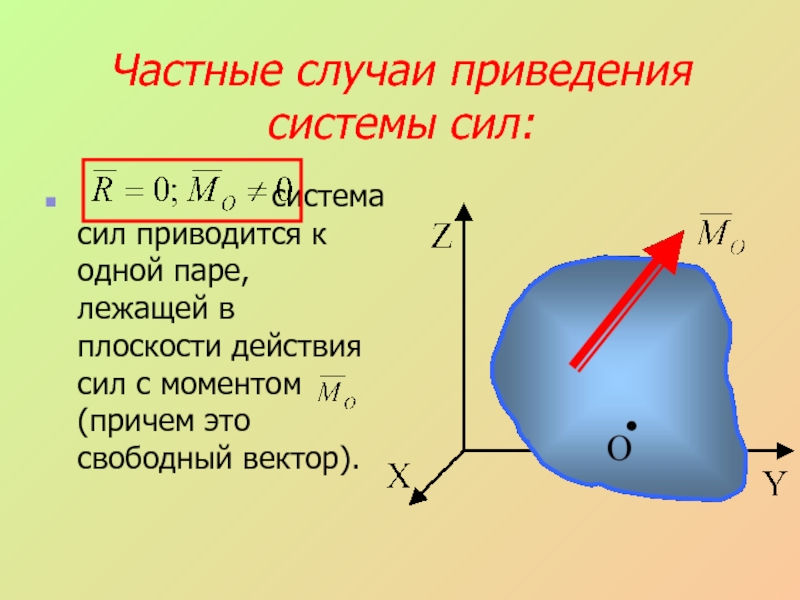
- 26. Частные случаи приведения системы сил:
- 27. система сил приводится
- 28. система сил уравновешена.
- 29. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ Необходимые
- 30. Основная форма условий равновесия для сил, лежащих
- 31. Вторая форма условий равновесия: Для равновесия произвольной
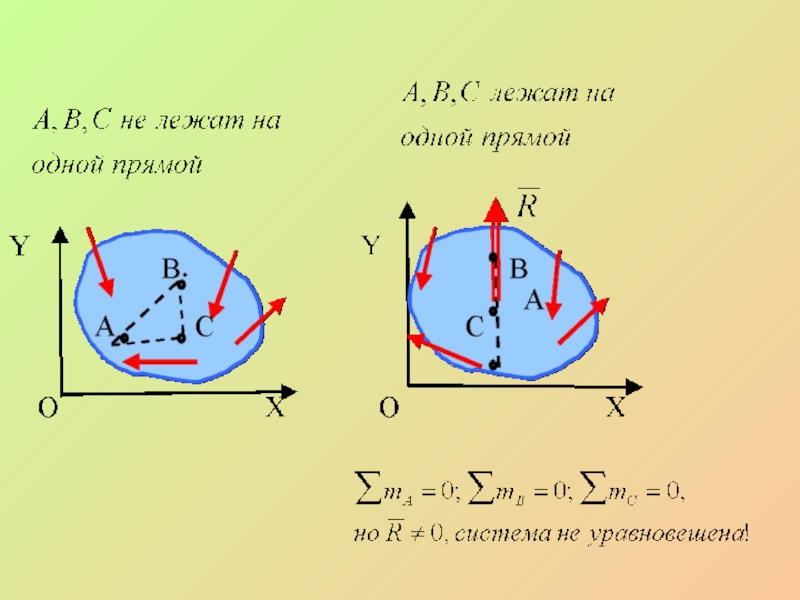
- 33. Третья форма условий равновесия Для равновесия
- 35. Для проверки решения задачи
Слайд 8Пьер Вариньон
Пьер Вариньон (фр. Pierre Varignon, Кан, Кан, 1654, Кан, 1654 — 23
Вариньон был другом НьютонаВариньон был другом Ньютона, ЛейбницаВариньон был другом Ньютона, Лейбница и БернуллиВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статикуВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механикуВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малыхВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрииВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханикеВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением ЛопиталяВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисленияВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 годуВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона. В работе «Новая механика или статика, проект которой был дан в 1687» (1725 В работе «Новая механика или статика, проект которой был дан в 1687» (1725) Вариньон дал систематическое изложение учения о сложении и разложении сил, о моментах сил и о правилах оперирования ими.[1]
Слайд 17Пуансо Луи
Пуансо (Poinsot) Луи (3.1.1777, Париж, — 5.12.1859, там же), французский
Слайд 18Теорема1 - О параллельном переносе силы
(лемма Пуансо):
силу , не
Слайд 21Теорема 2 – О приведении системы сил к заданному центру (теорема
Любая система сил , действующая на абсолютно твердое тело, при приведении к произвольному центру О заменяется главным вектором системы сил, приложенным в центре О и парой сил с моментом , равным главному моменту системы сил относительно центра О.
Слайд 24Используя теорему 1 перенесем все силы в центр О прибавляя пары
Слайд 25Для плоской системы сил главный вектор лежит в плоскости действия
X
Y
O
Z
X
Слайд 26Частные случаи приведения системы сил:
Слайд 27
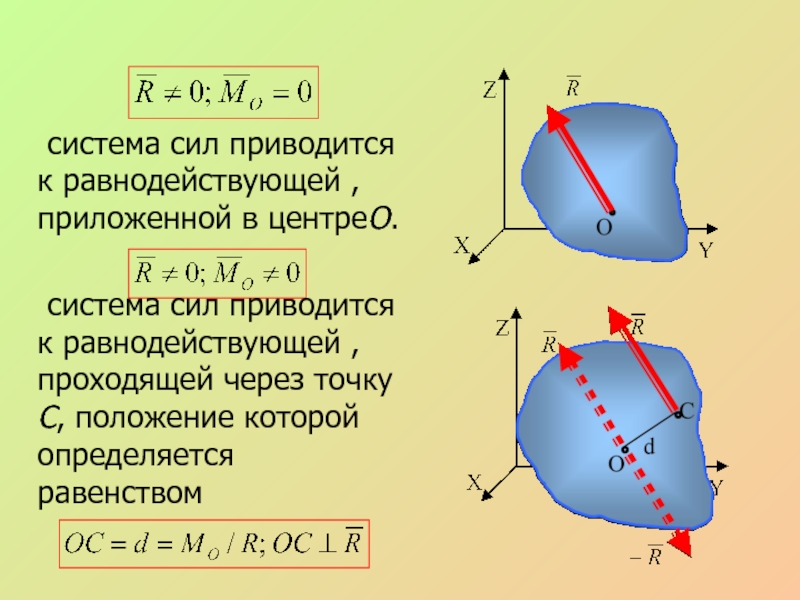
система сил приводится к равнодействующей , приложенной в центреО.
система сил приводится
Слайд 28
система сил уравновешена.
Теорема: Для равновесия любой системы сил необходимо
Слайд 29РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ
Необходимые и достаточные условия равновесия твердого
Из этих векторных уравнений следуют три формы аналитических условий равновесия.
Слайд 30Основная форма условий равновесия
для сил, лежащих в плоскости ОХУ:
Для равновесия произвольной
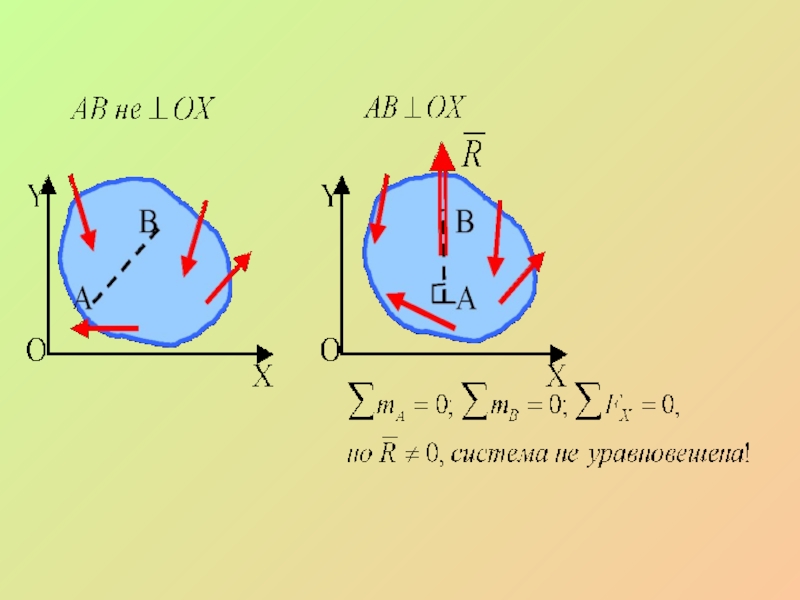
Слайд 31Вторая форма условий равновесия:
Для равновесия произвольной плоской системы сил необходимо и
не перпендикулярную прямой АВ, были равны нулю.
Слайд 33Третья форма условий равновесия
Для равновесия произвольной плоской системы сил необходимо и