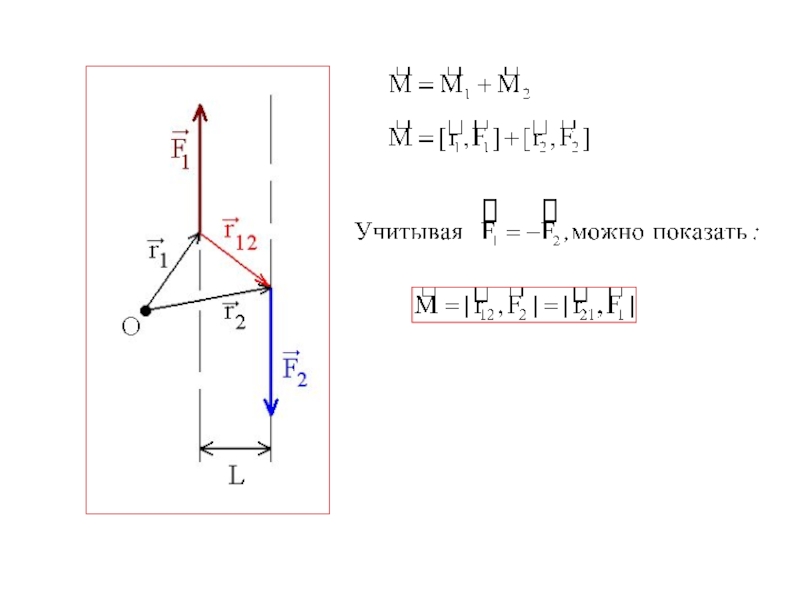
Определим момент пары сил относительно произвольной точки О.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Момент пары сил презентация
Содержание
- 1. Момент пары сил
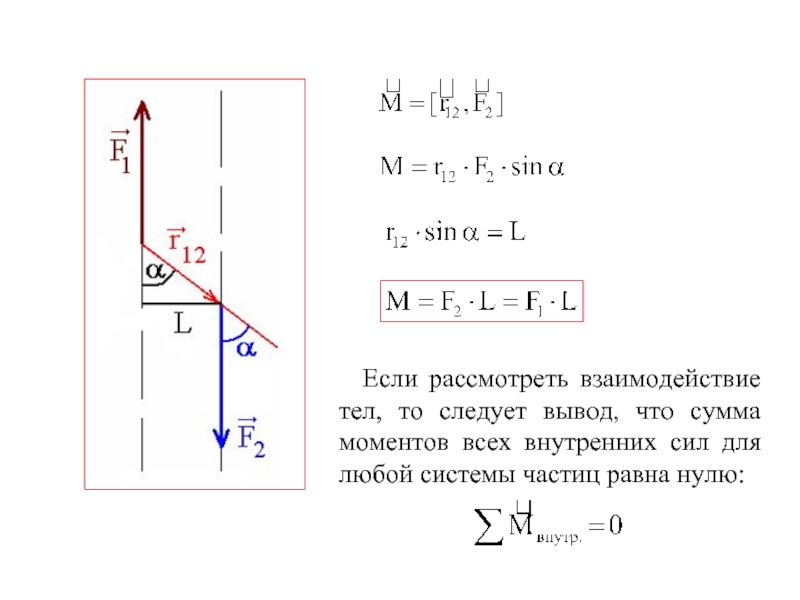
- 3. Если рассмотреть взаимодействие тел, то следует вывод,
- 4. МОМЕНТ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ Моментом импульса материальной
- 5. движение материальной точки по окружности
- 6. Момент импульса материальной точки относительно некоторой оси
- 7. Выясним, чем определяется изменение момента импульса со
- 8. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО НЕПОДВИЖНОЙ ОСИ
- 10. Тогда момент импульса всего тела относительно точки
- 11. Момент импульса тела относительно оси равен сумме
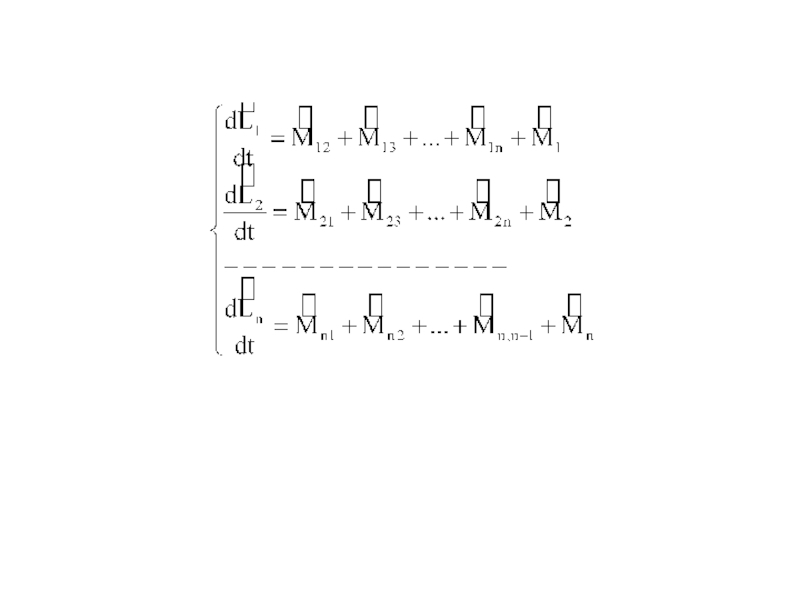
- 12. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Рассмотрим механическую систему, состоящую из n тел (материальных точек).
- 14. Сумма моментов внутренних сил системы тел равна нулю (рассмотрено ранее).
- 15. Закон сохранения момента импульса: Момент импульса замкнутой
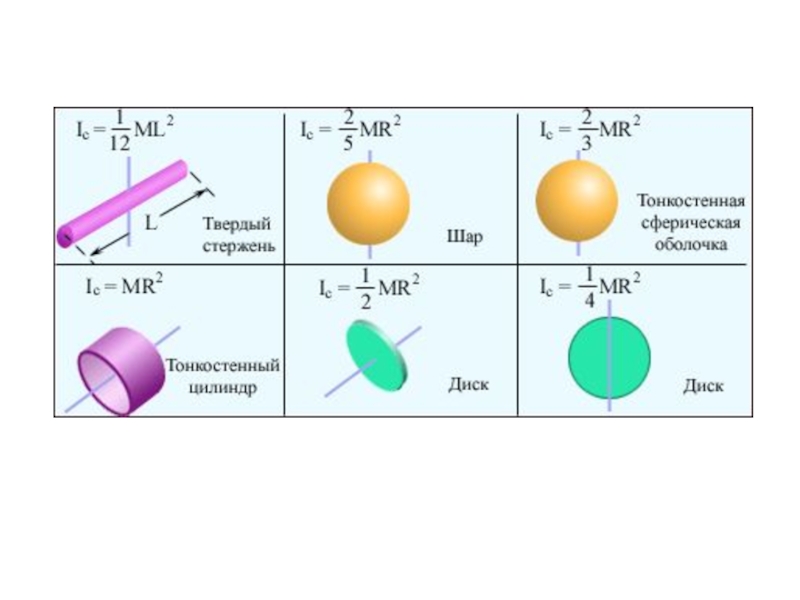
- 16. МОМЕНТ ИНЕРЦИИ Момент инерции - скалярная физическая
- 17. Представим произвольное тело как совокупность частиц (материальных
- 19. Момент инерции I относительно произвольной оси равен
- 20. ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Скорость
- 21. Запишем последнее равенство для каждой точки вращающегося
- 22. Учитывая, что момент инерции абсолютно твердого тела
- 23. Тогда окончательно получаем: Основной закон динамики
Если рассмотреть взаимодействие тел, то следует вывод, что сумма моментов всех внутренних сил для любой системы частиц равна нулю:
Слайд 1МОМЕНТ ПАРЫ СИЛ
Пара сил - это две равные по модулю и
противоположно направленные силы, не действующие вдоль одной прямой. Расстояние между прямыми вдоль которых действуют силы - плечо пары (L).
Слайд 3Если рассмотреть взаимодействие тел, то следует вывод, что сумма моментов всех
внутренних сил для любой системы частиц равна нулю:
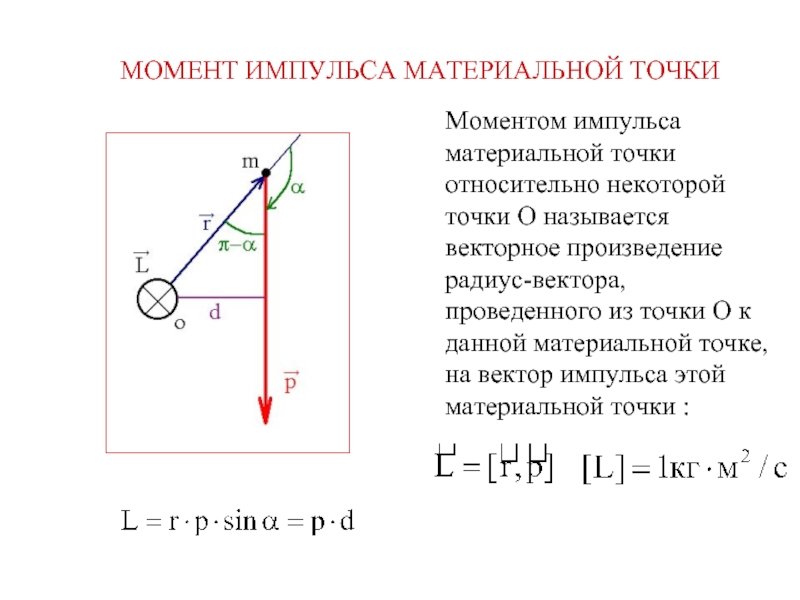
Слайд 4МОМЕНТ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ
Моментом импульса материальной точки относительно некоторой точки О
называется векторное произведение радиус-вектора, проведенного из точки О к данной материальной точке, на вектор импульса этой материальной точки :
Слайд 5
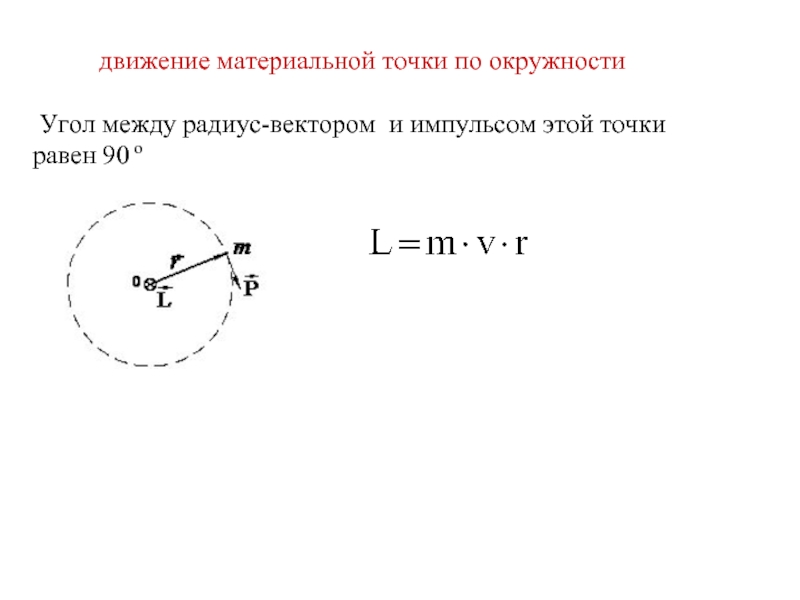
движение материальной точки по окружности
Угол между радиус-вектором и импульсом этой
точки равен 90 о
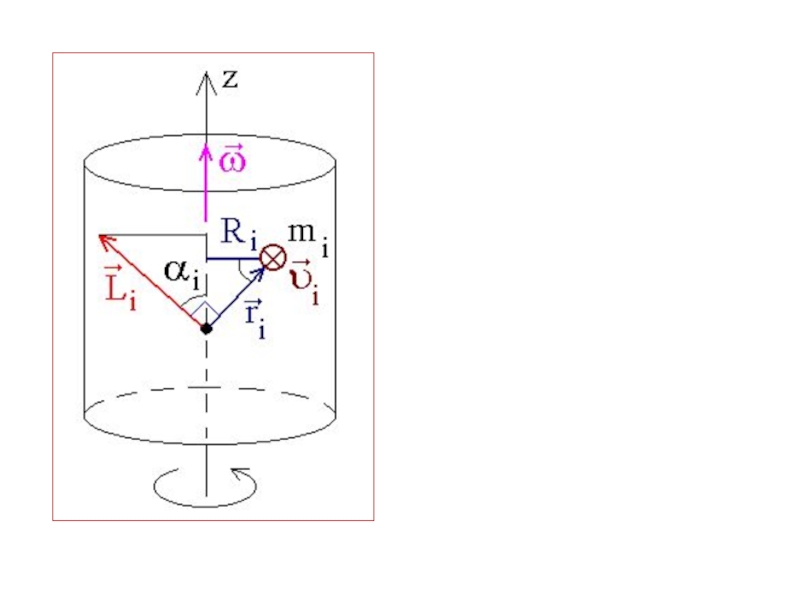
Слайд 6Момент импульса материальной точки относительно некоторой оси Z
Моментом импульса материальной точки
относительно произвольной оси Z называется проекция вектора момента импульса этой материальной точки относительно любой точки О, выбранной на оси Z, на данную ось
Слайд 7Выясним, чем определяется изменение момента импульса со временем:
Полученные равенства можно назвать
законом изменения момента импульса материальной точки.
Слайд 8МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО НЕПОДВИЖНОЙ ОСИ ВРАЩЕНИЯ
Момент импульса твердого тела
равен сумме моментов импульсов всех материальных точек, из которых состоит тело.
Выберем на оси Z произвольную точку О. Разобьем тело на материальные точки.
Момент импульса материальной точки относительно точки О равен
Слайд 10Тогда момент импульса всего тела относительно точки О :
Найдем момент импульса
тела относительно оси вращения Z.
Учтем взаимосвязь :
Тогда
Слайд 11Момент импульса тела относительно оси равен сумме моментов импульсов всех точек
этого тела относительно этой оси:
Таким образом, момент импульса тела относительно оси не зависит от выбора положения точки О.
Слайд 12ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Рассмотрим механическую систему, состоящую из n тел
(материальных
точек).
Слайд 15Закон сохранения момента импульса: Момент импульса замкнутой системы тел остается постоянным.
В
частном случае : если Мвнешн. (z) = 0, то Lz = const.
Если вращение взаимодействующих тел относительно некоторой неподвижной оси Z. В этом случае может сохраняться суммарный момент импульса системы относительно данной оси Lz.
Слайд 16МОМЕНТ ИНЕРЦИИ
Момент инерции - скалярная физическая величина, характеризующая инертные свойства тел
при вращательном движении.
Момент инерции материальной точки относительно оси:
[I] = 1 кг ⋅ м2
Слайд 17Представим произвольное тело как совокупность частиц (материальных точек). Тогда момент инерции
этого тела относительно заданной оси вращения равен:
Слайд 19Момент инерции I относительно произвольной оси равен сумме момента инерции I0
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями.
Слайд 20ОСНОВНОЙ ЗАКОН
ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Скорость изменения момента импульса материальной точки равна
моменту сил, действующих на эту точку. Подобное утверждение справедливо и для момента импульса материальной точки относительно некоторой оси Z:
Данные равенства можно назвать законом изменения момента импульса материальной точки.
Слайд 21Запишем последнее равенство для каждой точки вращающегося тела, а затем просуммируем
по всем точкам тела:
В последнем равенстве Lz – момент импульса тела относительно оси Z,
Тогда для всего тела
Слайд 22Учитывая, что момент инерции абсолютно твердого тела – постоянная величина, получим:
обозначим
εz – проекция вектора углового ускорения на ось Z
Было получено, что
Тогда
Слайд 23Тогда окончательно получаем:
Основной закон динамики вращательного движения твердого тела относительно неподвижной
оси. Его можно записать и для модулей входящих в него величин:
Закон динамики вращательного движения: Модуль углового ускорения тела прямо пропорционален модулю суммарного момента внешних сил, приложенных к телу и обратно пропорционален моменту инерции тела.
