Объект исследования: макроскопические системы - объекты, состоящие из очень большого числа частиц (молекул, атомов).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Молекулярная физика и термодинамика презентация
Содержание
- 1. Молекулярная физика и термодинамика
- 2. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
- 3. Основы классической статистики заложены
- 4. В средине XIX века была сформулирована молекулярно-кинетическая
- 5. Проверка факта, что атомы и молекулы
- 6. Закономерности, обусловленные большим числом сталкивающихся атомов и
- 7. Сколько времени вы проводите за компьютером? t,
- 8. информация по зарплатам за 2007-й год
- 9. 1. Распределение Максвелла (для описания распределения молекул по скоростям)
- 10. Обозначим: dN – число молекул
- 11. – условие
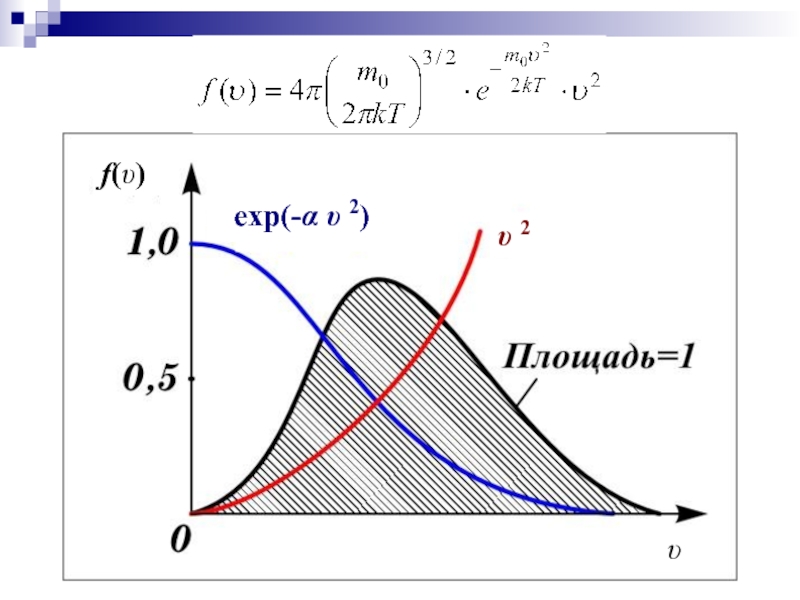
- 12. Явный вид функции f(υ) был получен теоретически
- 13. f(υ) υ υ 2 exp(-α υ 2)
- 14. Основные свойства функции распределения 1. При
- 15. при Т= const при m= const 3.
- 17. ПРИМЕНЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА Нахождение относительного числа
- 18. –относительное число молекул со скоростями от υ1
- 19. 2. Нахождение средней скорости молекул υср
- 20. - сумма скоростей молекул, скорости которых
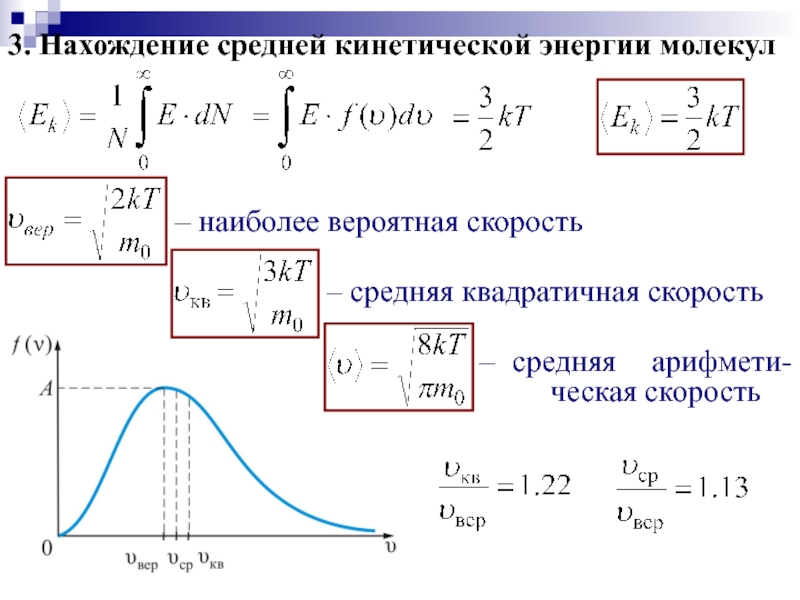
- 21. 3. Нахождение средней кинетической энергии молекул
- 22. 2. Распределение Больцмана (для описания распределения молекул по высоте в гравитационном поле Земли)
- 23. ИДЕАЛЬНЫЙ ГАЗ В ОДНОРОДНОМ ПОЛЕ ТЯГОТЕНИЯ
- 24. Т, g, µ, R
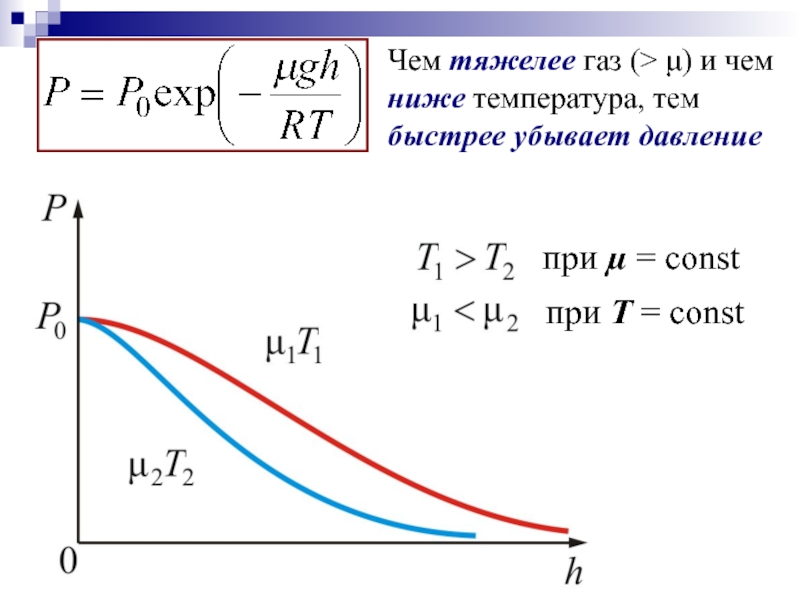
- 25. Чем тяжелее газ (> μ) и чем ниже температура, тем быстрее убывает давление
- 26. Распределение Больцмана определяет распределение частиц в силовом
- 27. с уменьшением температуры число молекул на высотах,
- 28. Еп = m0gh – потенциальная энергия одной
- 30. ЯВЛЕНИЯ ПЕРЕНОСА в неравновесных системах
- 31. Средняя длина свободного пробега молекул – это
- 32. Эффективный диаметр молекулы dэф –
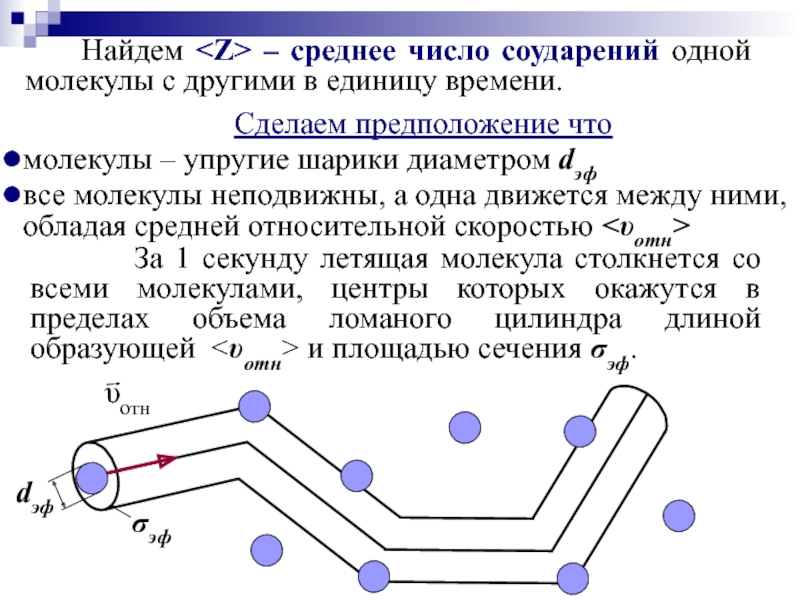
- 33. Сделаем предположение что молекулы
- 34. – объем цилиндра
- 35. При нормальных условиях (Т =
- 36. 1.V = const => P/T= const,
- 37. Явления переноса – круг явлений в термодинами-чески
- 38. А) Диффузия – процесс переноса массы вещества
- 39. Математически диффузия описывается законом Фика При
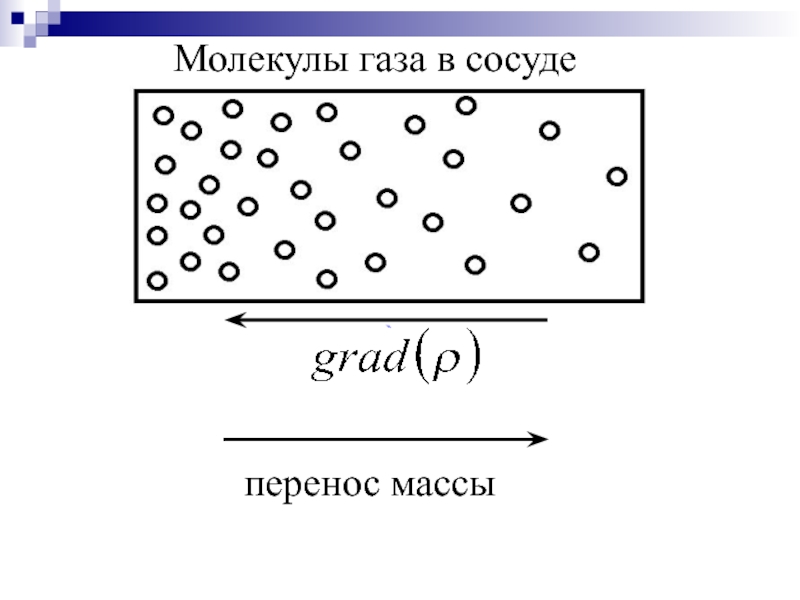
- 40. перенос массы Молекулы газа в сосуде
- 41. Градиент (от лат. gradiens, род. падеж gradientis
- 42. D – коэффициент диффузии
- 43. Диффузия через пористую перегородку
- 44. Прибор Анселя
- 45. Б) Внутреннее трение (вязкость)
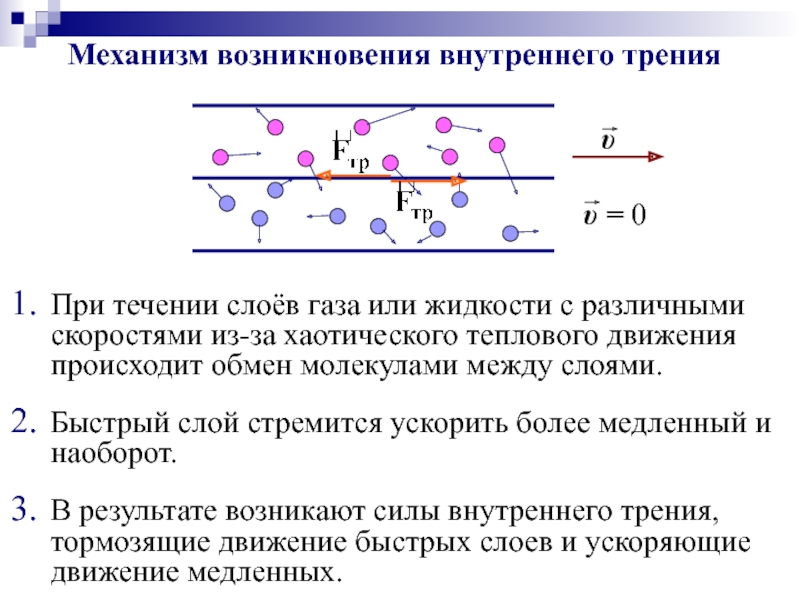
- 46. Механизм возникновения внутреннего трения В
- 47. Внутреннее трение подчиняется закону Ньютона:
- 48. – динамическая вязкость (коэффициент
- 50. В) Теплопроводность – процесс
- 51. Хаотично двигаясь, молекулы будут переходить из
- 52. Процесс теплопроводности описывается законом Фурье:
- 53. Знак «–» показывает,
- 54. Коэффициент теплопроводности численно равен
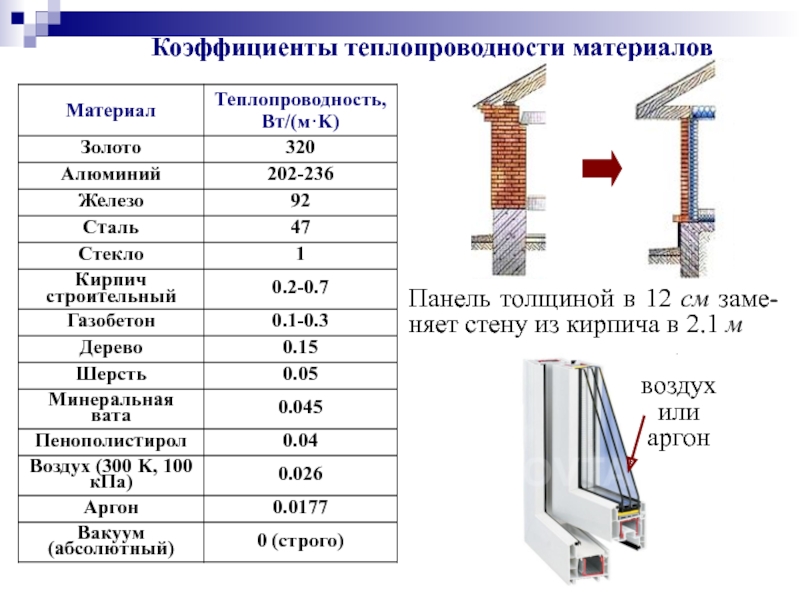
- 55. воздух или аргон Коэффициенты теплопроводности материалов
- 56. Теплопроводность газов
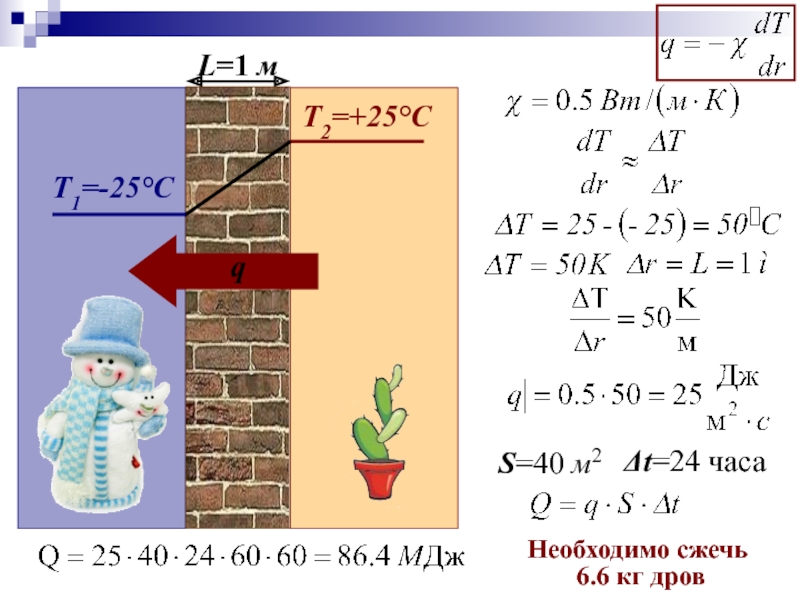
- 57. S=40 м2 Δt=24 часа Необходимо сжечь 6.6 кг дров
- 58. Связь коэффициентов переноса с величинами, характеризующими движение молекул газа
Слайд 1 Молекулярная физика и термодинамика – разделы физики, в
Слайд 3 Основы классической статистики заложены Д.К.Максвеллом (Англия), Л.Больцманом (Германия),
Задачи статистики
1. Нахождение средних и наиболее вероятных значений физических характеристик частиц, образующих макроскопическую систему.
2. Выяснение связи между характеристиками отдельных частиц системы и параметрами всей системы.
Слайд 4В средине XIX века была сформулирована молекулярно-кинетическая теория, но тогда не
=
µ
=
R
=
ρ
Пр: При плотности азота, равной 1.25 кг/м3, при t=0°С и Р=1 атм., υ=500м/с.
Для водорода: υ=2000м/с.
=
Слайд 5
Проверка факта, что атомы и молекулы идеальных газов в термически равновесном
Место попадания самых быстрых молекул
Место попадания самых медленных молекул
Распределение молекул по скоростям
T=1200ºC
Теория: υкв=584 м/с
560≤υ≤640 м/с
Эксперимент:
Слайд 6Закономерности, обусловленные большим числом сталкивающихся атомов и молекул, и не свойственные
По определению: Вероятность Р можно представить как отношение числа благоприятных случаев к числу возможных случаев.
Отсюда следует, что Р может принимать значения от нуля до единицы.
«Сколько молекул обладает скоростями, лежащими в интервале, включающем заданную скорость».
Например: на переписи населения, когда указывается возраст 18 лет – это не значит, что 18 лет, 0 часов, 0 минут. Эта цифра свидетельствует, что возраст лежит в интервале от 18 до 19 лет.
Распределение вероятностей – это закон, описываю-щий область значений переменной и вероятность появления переменной в конкретных областях значений.
Статистический анализ, для построения рядов распределения, проводится во многих областях науки с целью выделения характерных свойств и закономерностей изучаемой совокупности.
Слайд 7Сколько времени вы проводите за компьютером?
t, часы
Для корректного построения распределения нужно
Слайд 10 Обозначим:
dN – число молекул со скоростями от υ до
N – общее число молекул газа в данном объеме.
– относительное число молекул, скорости которых лежат в интервале от υ до υ + dυ (вероятность того, что скорость данной молекулы лежит в данном интервале ).
– относительное число молекул в единичном интервале скоростей.
– плотность вероятности того, что молекула обладает скоростью υ (функция распределения Максвелла).
Слайд 11
– условие нормировки функции распределения
Интеграл определяет
Слайд 12Явный вид функции f(υ) был получен теоретически Максвеллом в 1859 г.
m0
Т – абсолютная температура газа,
υ – заданная скорость (аргумент функции).
– постоянная Больцмана;
Распределение Максвелла справедливо для газов и жидкостей.
Слайд 14Основные свойства функции распределения
1. При υ=0 и υ=∞ f (υ)=0
– очень большие и маленькие скорости маловероятны
2. При увеличении температуры Vвер – увеличивается
2. Существует υвер – наиболее вероятная скорость, с которой движется большинство молекул. Ей соответствует максимум функции распределения Максвелла.
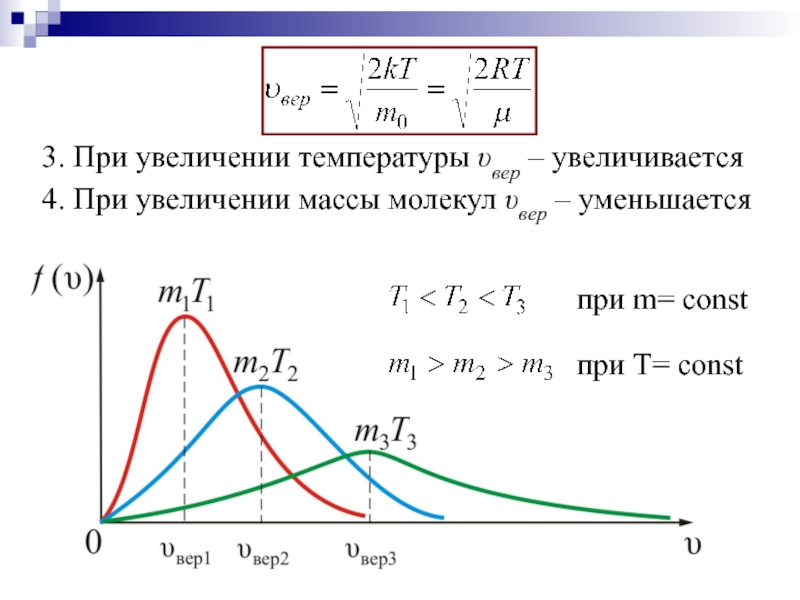
Слайд 15при Т= const
при m= const
3. При увеличении температуры υвер – увеличивается
4. При увеличении массы молекул υвер – уменьшается
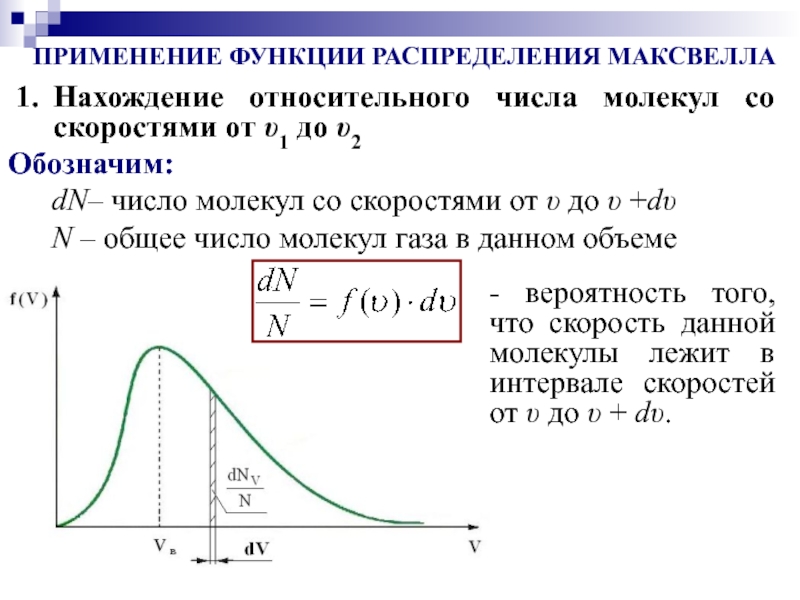
Слайд 17ПРИМЕНЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
Нахождение относительного числа молекул со скоростями от υ1
dN– число молекул со скоростями от υ до υ +dυ
Обозначим:
N – общее число молекул газа в данном объеме
- вероятность того, что скорость данной молекулы лежит в интервале скоростей от υ до υ + dυ.
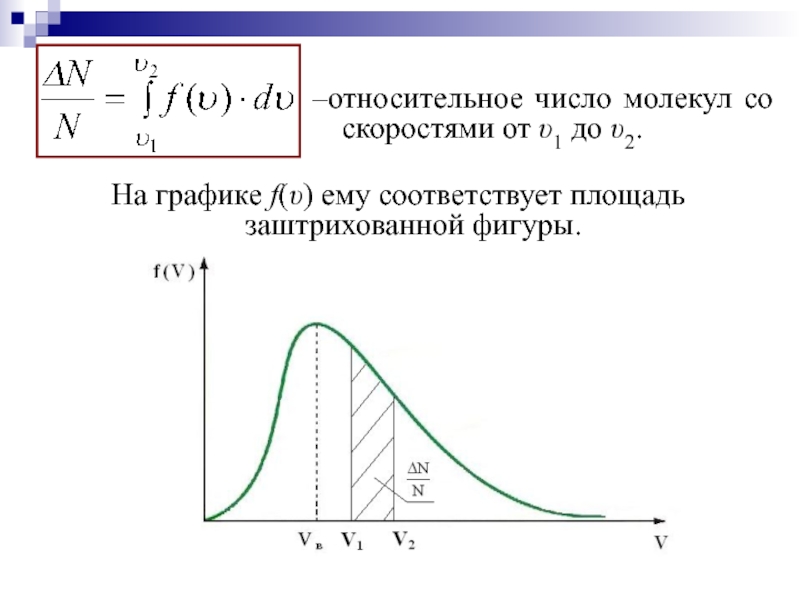
Слайд 18–относительное число молекул со скоростями от υ1 до υ2.
На графике f(υ)
Слайд 19
2. Нахождение средней скорости молекул υср
По определению:
Разобьем весь
dN – число молекул, скорости которых лежат в пределах одного из таких интервалов.
Так как dυ - элементарный интервал, то можно считать, что все скорости, принадлежащие этому интервалу, одинаковы и равны υ.
Слайд 20- сумма скоростей молекул, скорости которых
лежат в интервале от υ
Тогда сумма скоростей всех молекул:
Слайд 213. Нахождение средней кинетической энергии молекул
– наиболее вероятная скорость
– средняя квадратичная
– средняя арифмети-ческая скорость
Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. Закон статистический и выполняется тем лучше, чем больше число молекул.
Слайд 222. Распределение Больцмана
(для описания распределения молекул по высоте в гравитационном поле
Слайд 23ИДЕАЛЬНЫЙ ГАЗ В ОДНОРОДНОМ ПОЛЕ ТЯГОТЕНИЯ
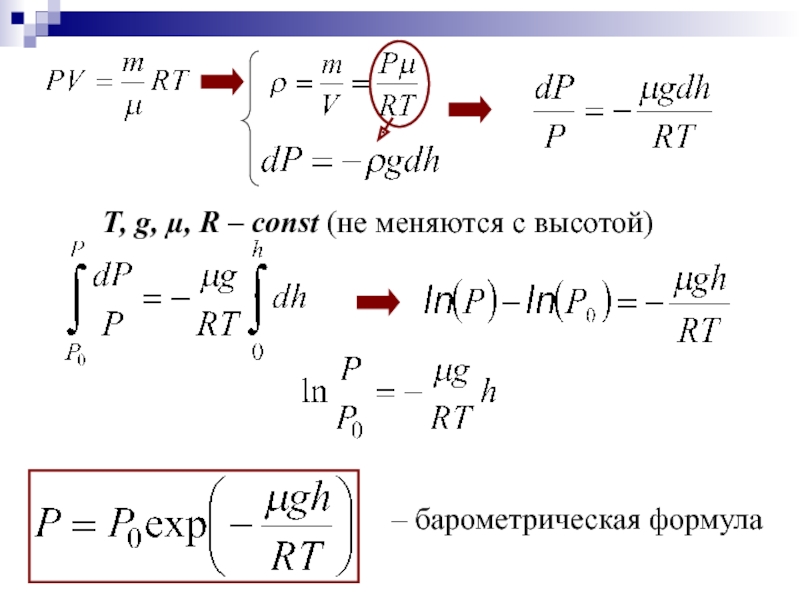
БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
Выделим условно столб воздуха и на некоторой высоте h от поверхности Земли выберем сечение столба S.
Атмосферное давление на высоте h обусловлено весом вышележащих слоев газа.
Р - давление на высоте h
(P + dP) - давление на высоте (h + dh)
dh > 0 dP < 0
– изменение давления с увеличением высоты
ρ – плотность газа
g – ускорение свободного падения
(на большей высоте давление меньше)
h+dh
h
P+dP
P
Слайд 24
Т, g, µ, R – const (не меняются с высотой)
- дифференциальное
– барометрическая формула
Слайд 26Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового
РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
P0 и n0 – давление и концентрация газа на нулевой высоте, P и n – на высоте h
распределение Больцмана в поле силы тяжести
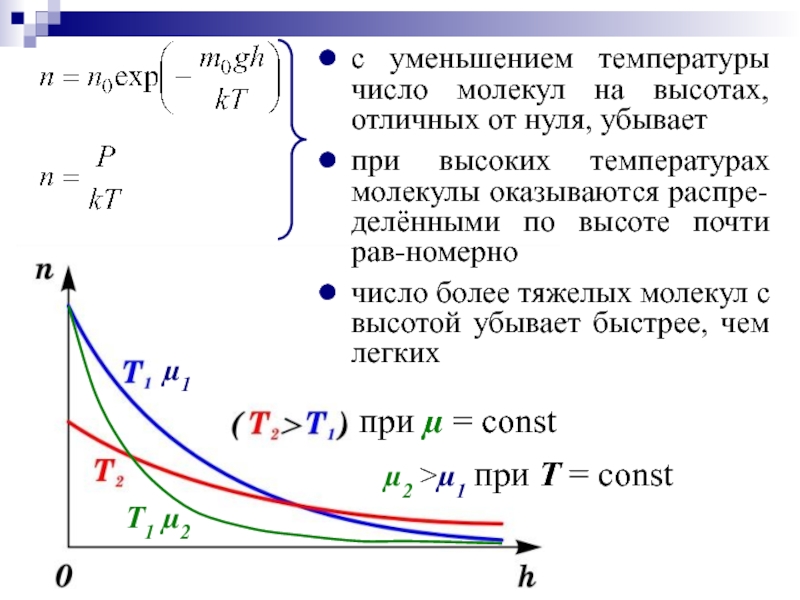
Слайд 27с уменьшением температуры число молекул на высотах, отличных от нуля, убывает
при
число более тяжелых молекул с высотой убывает быстрее, чем легких
Слайд 28Еп = m0gh – потенциальная энергия одной молекулы в поле тяготения
n0 – концентрация частиц в том месте, где Eп = 0
Оно устанавливается в результате совместного действия потенциального поля и теплового движения.
– распределение Больцмана характе-ризует распределение частиц по зна-чениям потенциальной энергии
Распределение справедливо в любом потенциальном поле сил для совокупности любых частиц, находящихся в состоянии хаотического теплового движения.
Слайд 31Средняя длина свободного пробега молекул – это среднее расстояние, которое
1. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ И СРЕДНЕЕ ЧИСЛО СТОЛКНОВЕНИЙ
λ1
λ2
λ3
λ4
Слайд 32
Эффективный диаметр молекулы dэф – минималь-ное расстояние, на которое сближаются центры
определяется природой самого газа (увеличивается при увеличе-нии размеров молекул)
зависит от скорости сталки-вающихся молекул, т.е. от темпе-ратуры (уменьшается при увели-чении температуры)
Эффективное сечение молекул σэф – площадь круга с радиусом, равным эффективному диаметру (площадь в которую не может проникнуть центр любой другой молекулы).
dэф
σэф
Слайд 33 Сделаем предположение что
молекулы – упругие шарики диаметром dэф
все
Найдем За 1 секунду летящая молекула столкнется со всеми молекулами, центры которых окажутся в пределах объема ломаного цилиндра длиной образующей <υотн> и площадью сечения σэф.
Слайд 34
– объем цилиндра
– среднее число соударений одной молекулы с
<υ> – средняя скорость молекулы, или путь, пройденный ею за 1 с.
– средняя длина свободного пробега молекулы:
Слайд 36
1.V = const => P/T= const, но диаметр слабо уменьша-ется с
2. Р=const. С ростом температуры <λ> увеличивается практически пропорционально температуре.
3. Т=const. С увеличением давления <λ> уменьшается.
Если <λ> сравнима или больше размеров сосуда L в котором находится газ, то такое состояние газа называется вакуумом.
ВАКУУМ
Средний
Высокий
Сверхвысокий
<λ> ≤ L
<λ> > L
<λ> >> L
Слайд 37Явления переноса – круг явлений в термодинами-чески неравновесных системах, в процессе
Процессы выравнивания сопровождаются направ-ленным переносом ряда физических величин (массы, энергии, импульса и т.д.) и поэтому называются явлениями переноса.
2. ЯВЛЕНИЯ ПЕРЕНОСА
К явлениям переноса в газах относятся
А) диффузия,
Б) внутреннее трение (вязкость),
В) теплопроводность.
Слайд 38А) Диффузия – процесс переноса массы вещества молекулами за счет их
Диффузия имеет место в газах, жидкостях и твердых телах
Слайд 39Математически диффузия описывается законом Фика
При диффузии масса переносится из мест с
Слайд 41Градиент (от лат. gradiens, род. падеж gradientis — шагающий) –вектор который
А(x,y,z) – скалярная функция
A → ρ
ρ
перенос массы
r
ρ (r)
Слайд 42D – коэффициент диффузии
Знак «–» показывает, что перенос
Согласно кинетической теории газов:
<υ> – средняя скорость молекул
<λ> – средняя длина свободного пробега молекул
–диффузионный поток через единицу площади в единицу времени (плотность потока массы)
Слайд 45 Б) Внутреннее трение (вязкость) – возникновение силы внутреннего
Слайд 46 Механизм возникновения внутреннего трения
В результате возникают силы внутреннего трения,
Быстрый слой стремится ускорить более медленный и наоборот.
При течении слоёв газа или жидкости с различными скоростями из-за хаотического теплового движения происходит обмен молекулами между слоями.
Слайд 47Внутреннее трение подчиняется закону Ньютона:
Вязкое трение в газе
Слайд 48
– динамическая вязкость (коэффициент вязкости)
ρ – плотность газа
– сила
Знак «–» означает, что направление переноса импульса и направление возрастания скорости противоположны.
Слайд 50 В) Теплопроводность – процесс выравнивания температуры, сопровождающийся направленным
Слайд 51 Хаотично двигаясь, молекулы будут переходить из одного слоя газа (жидкости)
Механизм возникновения теплопроводности
Это движение молекул приводит к перемешиванию молекул, имеющих различную кинетическую энергию.
В результате кинетическая энергия быстрых слоев уменьшается, а медленных – увеличивается.
Слайд 52Процесс теплопроводности описывается законом Фурье:
При теплопроводности энергия в виде тепла
Слайд 53
Знак «–» показывает, что при теплопроводности энергия переносится
– тепло переносимое через единицу площади в единицу времени (тепловой поток)
cV – удельная теплоемкость газа при постоянном объеме
χ – коэффициент теплопроводности
Согласно кинетической теории газов:
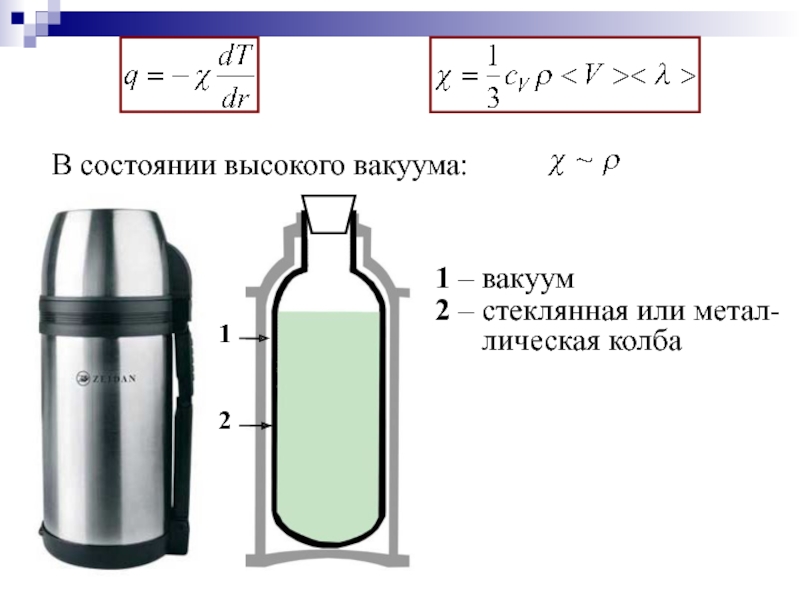
Слайд 54 Коэффициент теплопроводности численно равен количеству теплоты, переносимому через
В состоянии высокого вакуума:
1 – вакуум
2 – стеклянная или метал-лическая колба