- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование свойств металлов и сплавов. Метод молекулярной динамики презентация
Содержание
- 1. Моделирование свойств металлов и сплавов. Метод молекулярной динамики
- 2. Распределение занятий Лекции 16 ч. Лабораторные зaнятия 48 ч.
- 3. Литература Назаров А.А., Мулюков Р.Р. Атомистическое моделирование
- 4. Необходимость компьютерного моделирования в физике
- 5. Механические вычислительные устройства: счеты и арифмометр Арифмометр
- 6. Один из первых компьютеров: IBM-701 Процессор IBM-701
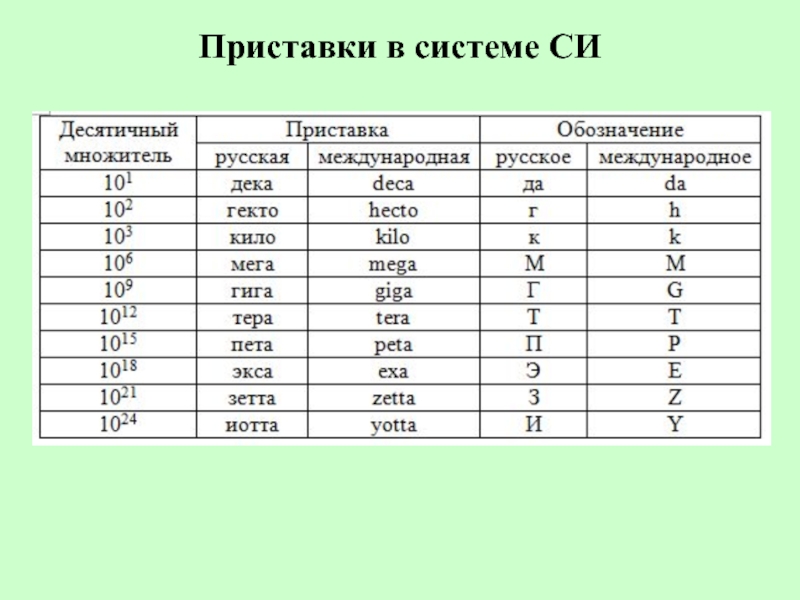
- 7. Приставки в системе СИ
- 8. Современные суперкомпьютеры Суперкомпьютер МГУ «Ломоносов» имеет производительность
- 9. Самые быстрые суперкомпьютеры мира На сайте http://top500.org
- 10. Экзафлопс суперкомпьютеры В Китае в 2017 г.
- 11. Знания, умения, навыки, необходимые для компьютерного моделирования
- 12. Многоуровневый характер структуры твердого тела
- 13. Электронная структура твердого тела: электроны и ядра
- 14. Атомная структура твердого тела В приближенном описании
- 15. Дефектная структура твердого тела Атомное строение
- 16. Микроструктура (зеренная структура) твердого тела Большинство используемых
- 17. Зеренная структура поликристалла: еще один экспериментальный пример Микроструктура поликристаллического тетрагонального оксида циркония
- 18. Структура твердотельных конструкций: макроскопические элементы Нога Эйфелевой
- 19. Необходимость компьютерного моделирования в физике конденсированных сред
- 20. Общая характеристика методов моделирования в физике материалов
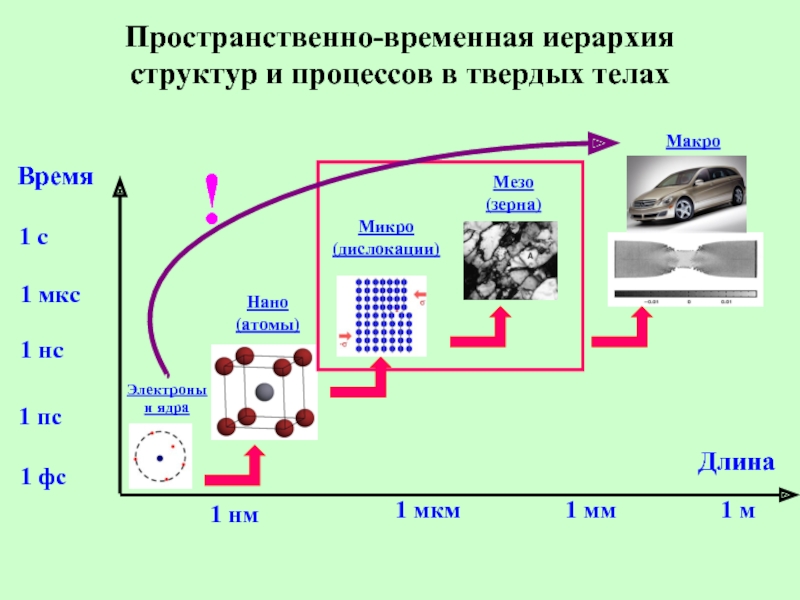
- 21. Пространственно-временная иерархия структур и процессов в твердых телах
- 22. Иерархия методов моделирования Из первых принципов
- 23. Фундаментальная основа моделирования из первых принципов Уравнение
- 24. Фундаментальная основа классической молекулярной динамики II закон Ньютона: Потенциальная энергия системы атомов:
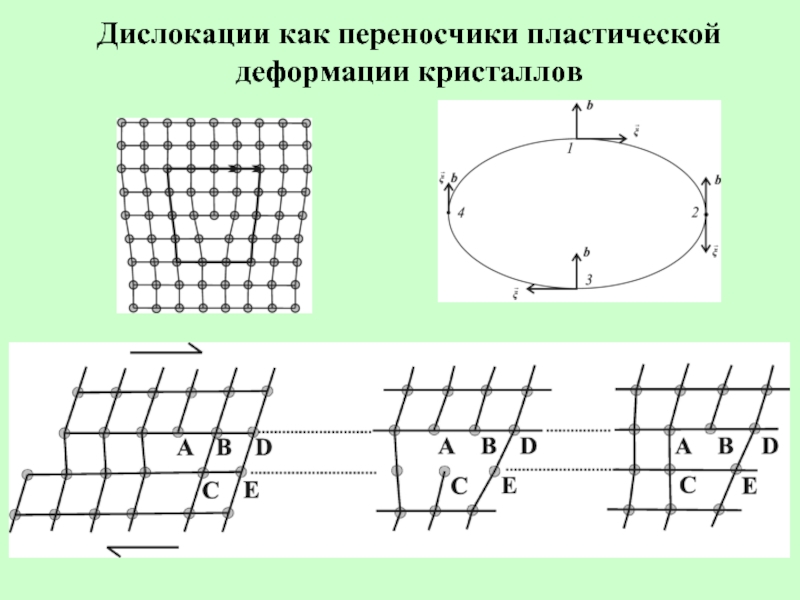
- 25. Дислокации как переносчики пластической деформации кристаллов
- 26. Фундаментальная основа дислокационного моделирования: дискретная дислокационная динамика
- 27. Работа источника Франка-Рида в монокристалле в
- 28. Результат 3D-ДДД моделирования M.C. Fivel, Model.
- 29. Двумерное дислокационное моделирование В.Н. Перевезенцев, Г.Ф.Сарафанов,
- 30. 2D-ДДД с тремя системами скольжения: моделирование отжига
- 31. Мезоскопическое (микромеханическое) моделирование crystal plasticity modeling) 1.
- 32. Примеры микромеханических моделей деформации поликристаллов Модель Закса
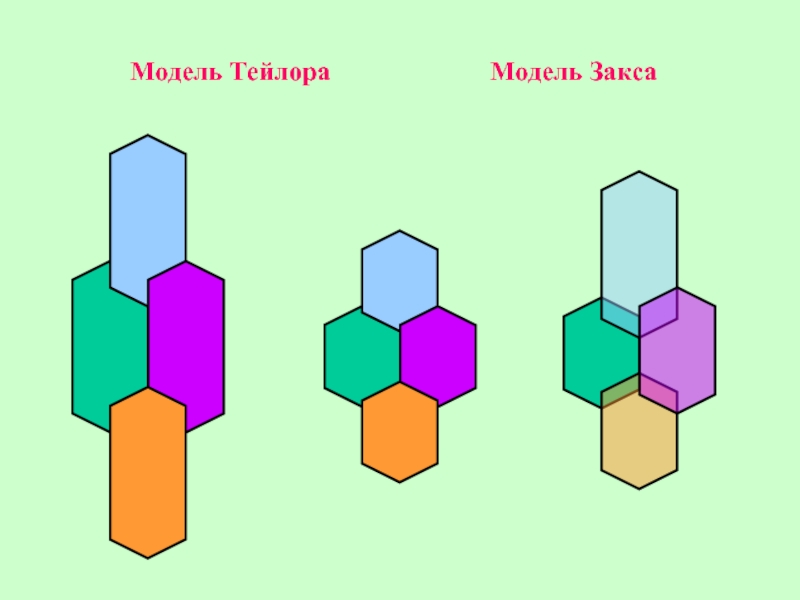
- 33. Модель Тейлора Модель Закса
- 34. Макромеханическое моделирование Уравнения равновесия упругодеформированного тела Метод конечных элементов
- 35. Макромеханическое моделирование РКУП W.J. Zhao, H.
- 36. Основной предмет нашего курса Среди методов моделирования
Слайд 1Моделирование свойств металлов и сплавов. Метод молекулярной динамики
Дисциплина по выбору
“Физика конденсированного состояния”
По кафедре ФТН
Слайд 2Распределение занятий
Лекции 16 ч.
Лабораторные зaнятия 48 ч.
Практические занятия 16 ч.
Отчетность экзамен
Требования к студенту:
Слайд 3Литература
Назаров А.А., Мулюков Р.Р. Атомистическое моделирование материалов, наноструктур и процессов нанотехнологии.
Ремеев И.С. Математическое моделирование физических процессов. – Уфа: БашГУ, 2010.
Гулд Х., Тобочник Я. Компьютерное моделирование в физике (в 2-х томах). М.: Мир, 1990.
Ибрагимов И.М., Ковшов А.Н., Назаров Ю.Ф. Основы компьютерного моделирования наносистем: Учебное пособие. СПб: Лань, 2010. 384 с.
Мансури Г.А. Принципы нанотехнологии. Исследование конденсированных веществ малых систем на молекулярном уровне. М.: Мир, 2008.
Слайд 4Необходимость компьютерного моделирования в физике
Число задач физики, имеющих
Уравнения движения 1, 2 тел. Задача 3 тел уже не решается аналитически.
Уравнение Шредингера для атома водорода. Задача не решаема точно уже для атома гелия.
…
Во всех остальных случаях возможно только численное решение с помощью компьютеров. Точность, скорость и широта применения численных методов растет с ростом возможностей вычислительных средств.
Слайд 5Механические вычислительные устройства: счеты и арифмометр
Арифмометр «Феликс» выпускался в Москве, Пензе,
Слайд 6Один из первых компьютеров: IBM-701
Процессор IBM-701 имел производительность менее 10 кфлопс.
Флопс – число операций с плавающей запятой в секунду
FLOPS=FLoating-point Operations Per Second
Слайд 8Современные суперкомпьютеры
Суперкомпьютер МГУ «Ломоносов» имеет производительность в 1,3 петафлопс, состоит из
1 пфлопс = 1015 флопс (операций с плавающей запятой в секунду)
FLOPS=FLoating-point Operations Per Second
Слайд 9Самые быстрые суперкомпьютеры мира
На сайте http://top500.org есть обновляющийся список наиболее производительных
Суперкомпьютеры жизненно важны для экономики, безопасности, научного развития стран, а также для демонстрации их технологического превосходства.
Слайд 10Экзафлопс суперкомпьютеры
В Китае в 2017 г. планируют запустить первый прототип суперкомпьютера
Слайд 11Знания, умения, навыки, необходимые для компьютерного моделирования
Знание физических законов и уравнений,
Знание численных методов решения математических задач
Умение составлять алгоритм численного решения математических задач
Умение программировать на языке высокого уровня (C, Fortran, Pascal, Basic etc.)
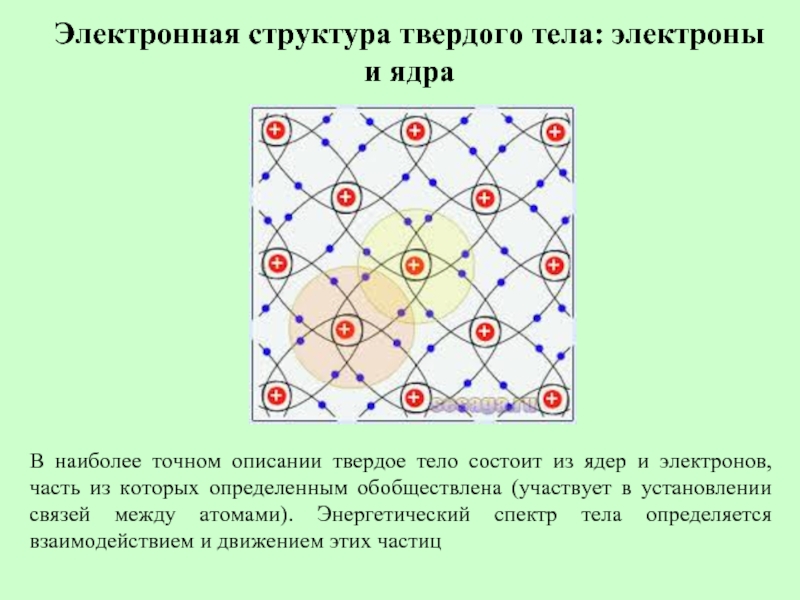
Слайд 13Электронная структура твердого тела: электроны и ядра
В наиболее точном описании твердое
Слайд 14Атомная структура твердого тела
В приближенном описании твердое тело можно рассматривать как
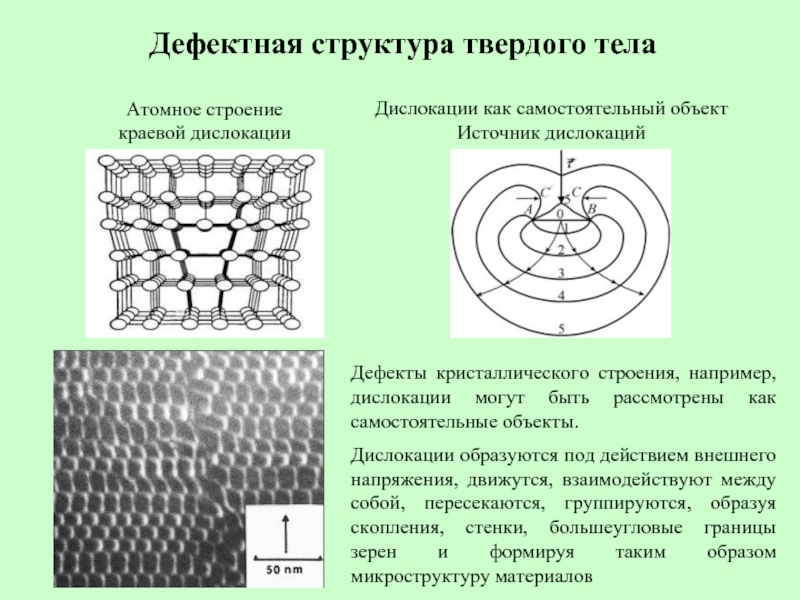
Слайд 15Дефектная структура твердого тела
Атомное строение
краевой дислокации
Дислокации как самостоятельный объект
Источник дислокаций
Дефекты
Дислокации образуются под действием внешнего напряжения, движутся, взаимодействуют между собой, пересекаются, группируются, образуя скопления, стенки, большеугловые границы зерен и формируя таким образом микроструктуру материалов
Слайд 16Микроструктура (зеренная структура) твердого тела
Большинство используемых материалов состоит из зерен (кристаллитов).
схема
микроскопия
Слайд 17Зеренная структура поликристалла: еще один экспериментальный пример
Микроструктура поликристаллического тетрагонального оксида циркония
Слайд 18Структура твердотельных конструкций: макроскопические элементы
Нога Эйфелевой башни
«Покосившийся мост» в Голландии (окружающая
При расчетах машин, строительных конструкций твердое тело рассматривается как сплошная среда с данными характеристиками, в качестве элементарных составляющих конструкций рассматриваются макроскопические элементы, имеющие масштаб, меньший характерных масштабов неоднородности. Однако свойства материала определяются его внутренним строением.
Слайд 19Необходимость компьютерного моделирования в физике конденсированных сред
1. Сложность структуры реальных
2. Протекание процессов с характерными временами в области от 1 пс до нескольких лет: от периода колебания решетки до характерных времен диффузии, накопления радиационных повреждений при облучении
3. В конечном итоге все свойства материалов определяются процессами, происходящими на атомном уровне, изучение которых невозможно аналитическими методами
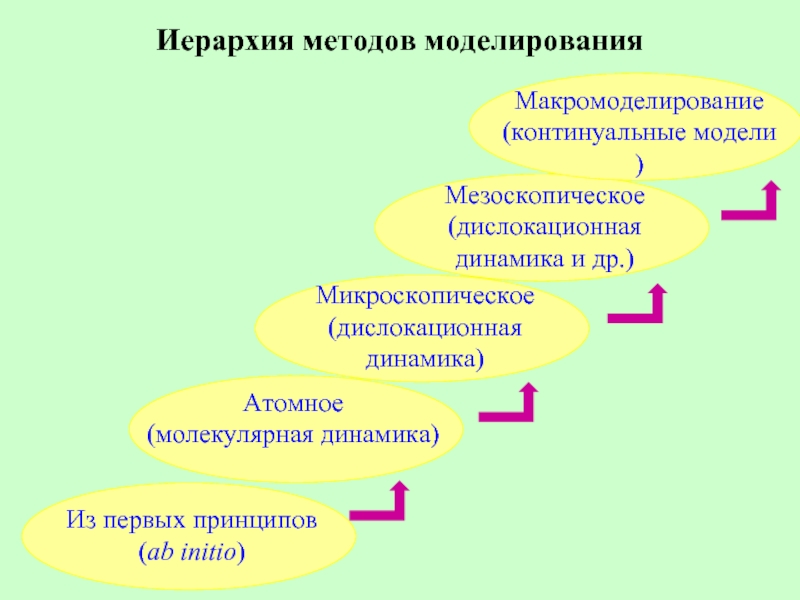
Слайд 22Иерархия методов моделирования
Из первых принципов (ab initio)
Атомное
(молекулярная динамика)
Мезоскопическое (дислокационная динамика
Макромоделирование (континуальные модели )
Микроскопическое (дислокационная динамика)
Слайд 23Фундаментальная основа моделирования из первых принципов
Уравнение Шредингера для системы атомов
Принципиально неразрешимая
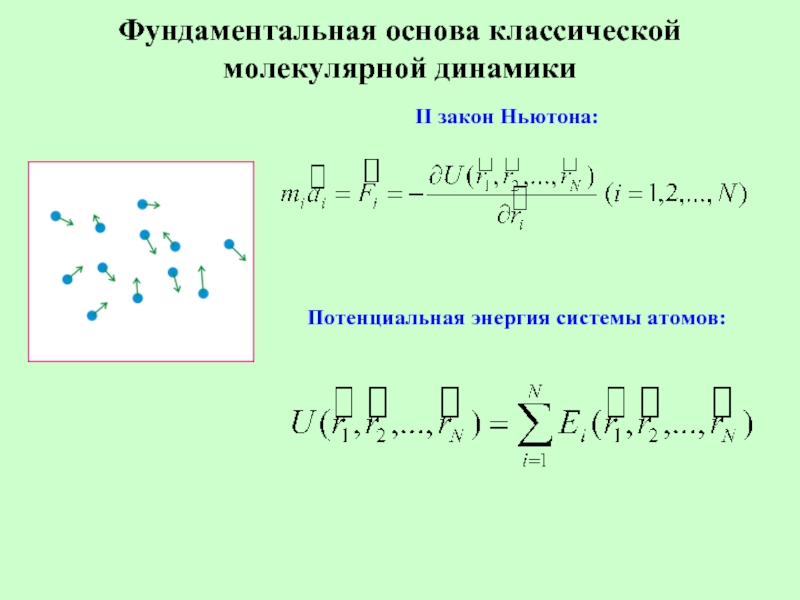
Слайд 24Фундаментальная основа классической молекулярной динамики
II закон Ньютона:
Потенциальная энергия системы атомов:
Слайд 26Фундаментальная основа дислокационного моделирования: дискретная дислокационная динамика (ДДД)
Проблемы: 1) Дальнодействующий характер
размножение дислокаций; 3) Линейный характер дефектов
Сила, действующая на сегмент:
Скорость движения сегмента:
Трехмерный случай (3D-ДДД)
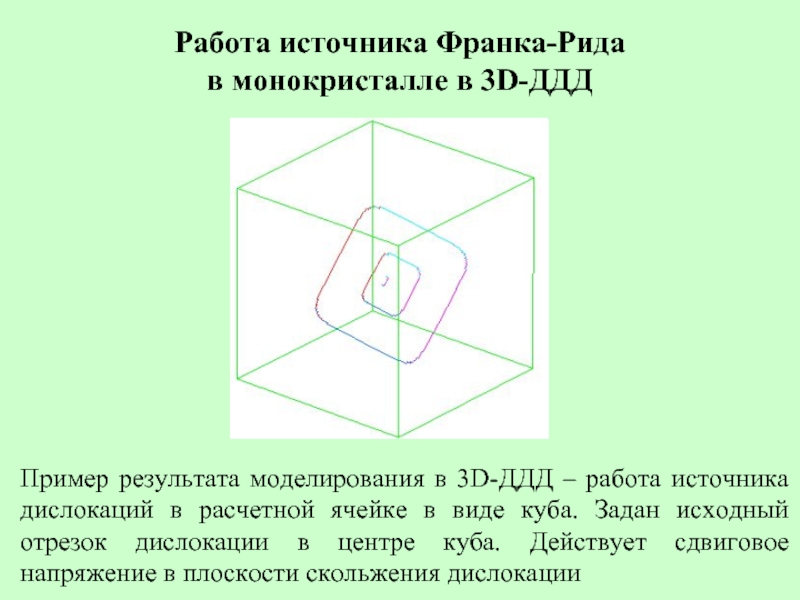
Слайд 27Работа источника Франка-Рида
в монокристалле в 3D-ДДД
Пример результата моделирования в 3D-ДДД
Слайд 28Результат 3D-ДДД моделирования
M.C. Fivel, Model. Simul. Mater. Sci. Eng. 1996
Степень
Плотность дислокаций и объем расчетов резко возрастает со степенью деформации (со временем). 3D дислокационная динамика пока не в состоянии дать полезную информацию о механизмах эволюции субструктуры при больших степенях деформации
http://www.gpm2.inpg.fr/axes/plast/microplast/ddd
Слайд 29Двумерное дислокационное моделирование В.Н. Перевезенцев, Г.Ф.Сарафанов, Письма в ЖТФ, 2007, 33(9)
В поле напряжений дисклинации дислокации выстраиваются в стенку, «достраивая» границу наклона, обрывающуюся на дисклинации. Хорошее согласие с экспериментом (В.В. Рыбин) и подтверждение качественной модели В.И. Владимирова и А.Е. Романова
Недостаток: рассматривается только одна система скольжения
В.В. Рыбин, 1987
В.И. Владимиров, А.Е. Романов, 1987
Слайд 302D-ДДД с тремя системами скольжения: моделирование отжига
B. Bako, I. Groma et
Исходное распределение дислокаций трех систем скольжения – хаотическое. Дислокациям разрешено скольжение и переползание. С течением времени в системе происходит самопроизвольная перестройка в упорядоченную ячеистую структуру под действием сил взаимодействия дислокаций (полигонизация)
Слайд 31Мезоскопическое (микромеханическое) моделирование crystal plasticity modeling)
1. Деформация кристалла происходит путем
плоскостям скольжения и в определенных направлениях (для г.ц.к. –
это {111}<110>. Дислокационная природа сдвига не рассматривается.
Кинетика деформации задается выражением:
Компоненты тензора напряжений
Компоненты тензора скоростей деформации
Компоненты тензора Шмидта
Пороговое напряжение сдвига по системе s
Нормирующий множитель
n >> 1
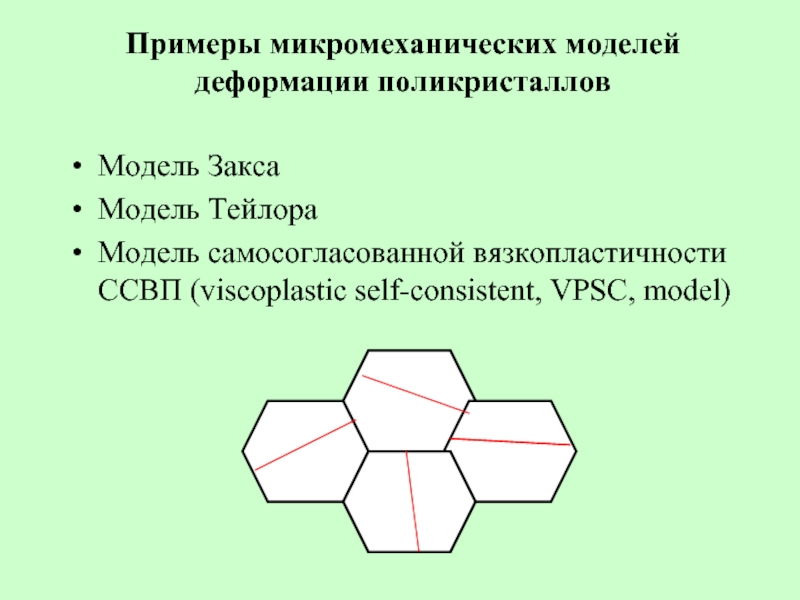
Слайд 32Примеры микромеханических моделей деформации поликристаллов
Модель Закса
Модель Тейлора
Модель самосогласованной вязкопластичности ССВП (viscoplastic
Слайд 34Макромеханическое моделирование
Уравнения равновесия
упругодеформированного тела
Метод конечных элементов
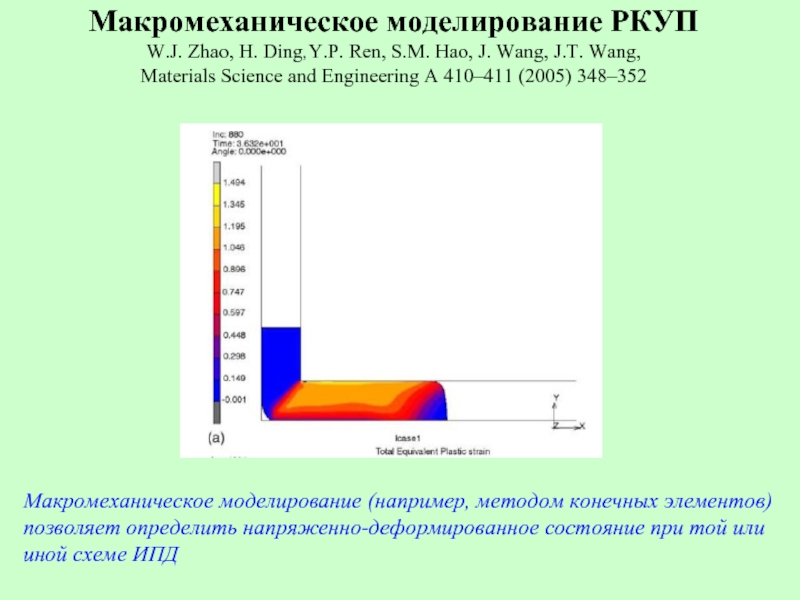
Слайд 35Макромеханическое моделирование РКУП W.J. Zhao, H. Ding,Y.P. Ren, S.M. Hao, J.
Макромеханическое моделирование (например, методом конечных элементов)
позволяет определить напряженно-деформированное состояние при той или
иной схеме ИПД
Слайд 36Основной предмет нашего курса
Среди методов моделирования одно из важнейших мест занимает
Поэтому задачей настоящего курса является изучение метода молекулярной динамики применительно к моделированию реальных кристаллических материалов, в том числе наноматериалов.