- ФПРВ амплитуд сигнала
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели радиолокационных сигналов. Синтез оптимальных обнаружителей сигналов презентация
Содержание
- 1. Модели радиолокационных сигналов. Синтез оптимальных обнаружителей сигналов
- 2. Синтез оптимальных обнаружителей сигналов Обнаружение одиночного радиоимпульса
- 5. В оптимальном приёмнике независимо от выбранного критерия
- 6. Определим вероятности ошибочных решений (F и
- 7. Для смеси сигнала с шумом Пороговый сигнал
- 8. Обнаружение сигнала со случайными параметрами
- 10. Т.к. I ′ >> I ″ (для доказательства используется метод «стационарной фазы»)
- 11. , Здесь
- 12. Характеристики обнаружения Zш – распределение
- 13. Модуль Zсш будет распределен по
- 14. Характеристика обнаружения D(q2) по сравнению
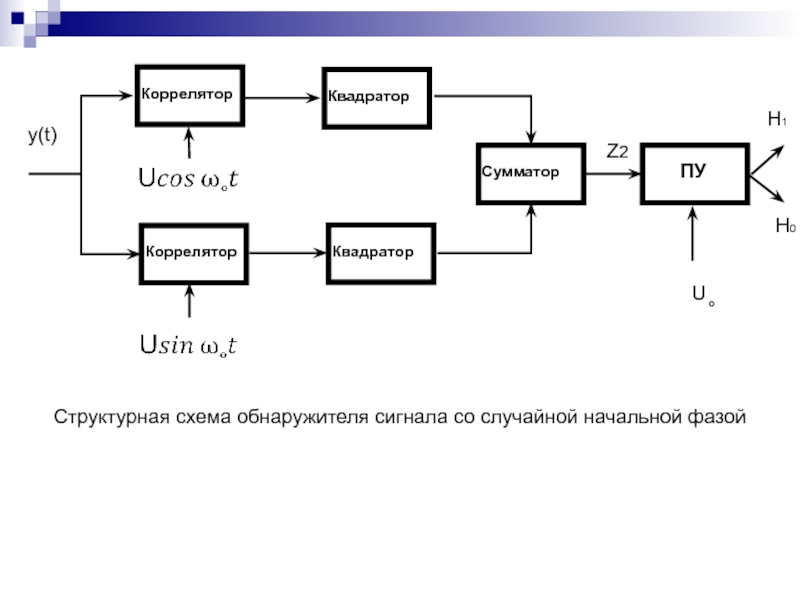
- 15. Структурная схема обнаружителя сигнала со случайной начальной фазой
- 16. Обнаружение сигнала со случайной амплитудой и
- 17. Структура обнаружителя аналогична варианту со случайной начальной
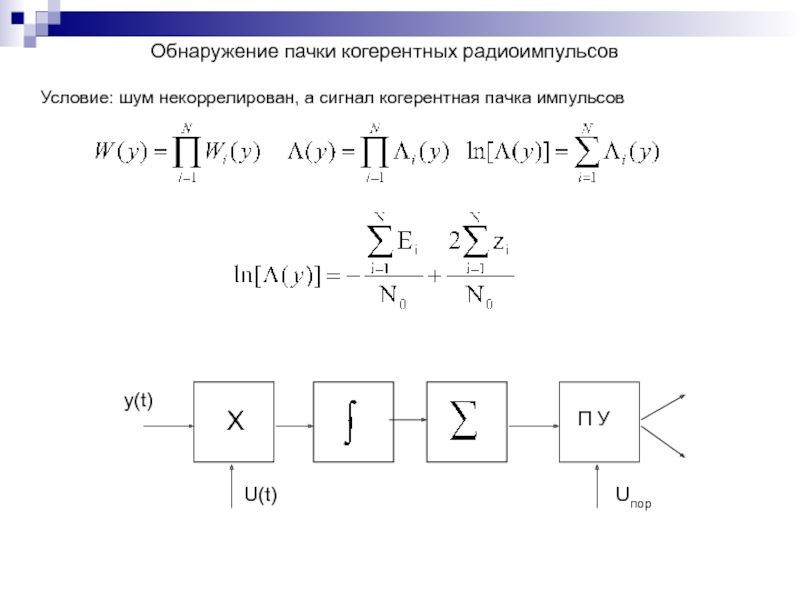
- 18. Обнаружение пачки когерентных радиоимпульсов Условие: шум некоррелирован, а сигнал когерентная пачка импульсов
- 19. Структура обнаружителя пачки с неизвестной начальной фазой
- 20. Оптимальная фильтрация Критерии построения оптимального фильтра: Минимума
- 21. Сигнал на выходе фильтра –
Слайд 1Модели радиолокационных сигналов
1. Детерминированный сигнал.
2. Сигнал со случайной начальной фазой.
3.Сигнал со
Слайд 2Синтез оптимальных обнаружителей сигналов
Обнаружение одиночного радиоимпульса с полностью известными параметрами на
Единственное, что предполагается заранее неизвестным, это сам факт наличия сигнала
T0=290°K , kT0= 4 ·10-21
Слайд 5В оптимальном приёмнике независимо от выбранного критерия должны выполняться следующие операции
а) входное напряжение приёмника y(t) нужно перемножить с опорным напряжением u(t), представляющим собой копию излученных передатчиком РЛС колебаний;
б) результат перемножения следует интегрировать (усреднить) за время существования сигнала T;
в) выходное напряжение интегратора необходимо сравнивать с некоторым постоянным напряжением, именуемым пороговым или просто порогом l0.
б) выходное напряжение интегратора
сравнивается с пороговым напряжением l0 =Uпор: если Uвых>Uпор, то принимается решение о наличии сигнала, и с вероятностью D это будет соответствовать действительности; при Uвых
Слайд 6Определим вероятности ошибочных решений (F и
Дисперсия на выходе коррелятора или
Следовательно, ФПРВ выходного шума имеет вид
Слайд 7Для смеси сигнала с шумом
Пороговый сигнал определяется как минимальное отношение сигнал-шум,
при
Слайд 8Обнаружение сигнала со случайными параметрами
Модель сигнала со случайными параметрами
α1, …
ОП - λ(y) определим, используя сведение сложной гипотезы к простой, т.е.
Сигнал с неизвестной начальной фазой u(t) = u(t, ϕ) = U(t)cos(w0t + ϕ)
[-π; π] или [0; 2π], W(ϕ). – закон распределения фазы.
W(ϕ) = 1/2π.
Слайд 12Характеристики обнаружения
Zш – распределение шума, Zсш – распределение смеси
Математическое ожидание составляющих равно х1ш и х2ш 0.
Дисперсия шума:
Слайд 13
Модуль Zсш будет распределен по закону Релея (Релея – Райса). Для
Нужно найти ее ФПРВ.
Слайд 14
Характеристика обнаружения D(q2) по сравнению со случаем известной начальной фазы смещается
Это связано с тем, что при неизвестной начальной фазе для обеспечения эквивалентного значения вероятности правильного обнаружения (по сравнению со случаем известных параметров сигнала) необходимо более высокое отношение с-ш.
Слайд 16Обнаружение сигнала со случайной амплитудой
и случайной начальной фазой
U(t) = AU(t)cos(ω0t + ϕ), ϕ → 0…2π,
U(t) в отличие от случайного сигнала с известными параметрами определяется статистически в результате усреднения по большому числу реализаций.
А – случайная величина, распределенная по закону Релея.
Слайд 17Структура обнаружителя аналогична варианту со случайной начальной фазой,
Отличие в величине порога
Дисперсия смеси сигнала с шумом
Условие равенства энергий
Слайд 18Обнаружение пачки когерентных радиоимпульсов
Условие: шум некоррелирован, а сигнал когерентная пачка импульсов
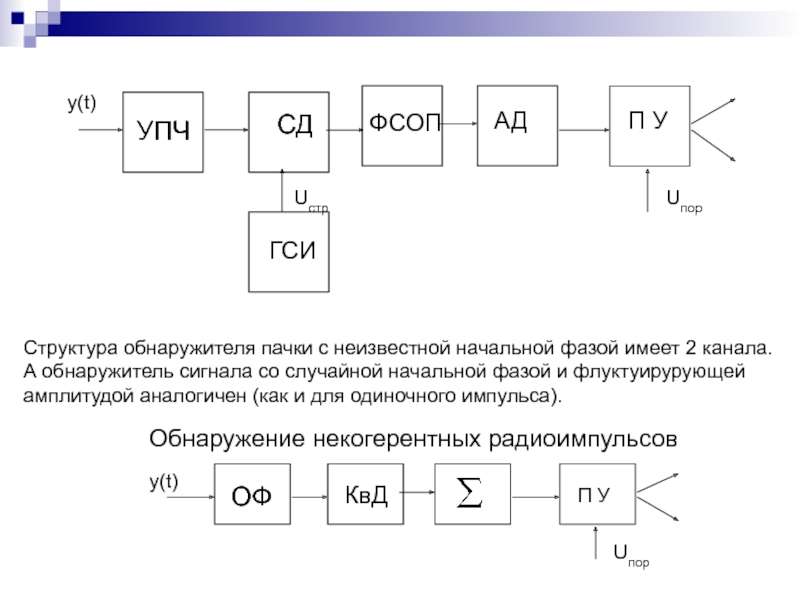
Слайд 19Структура обнаружителя пачки с неизвестной начальной фазой имеет 2 канала.
А обнаружитель
амплитудой аналогичен (как и для одиночного импульса).
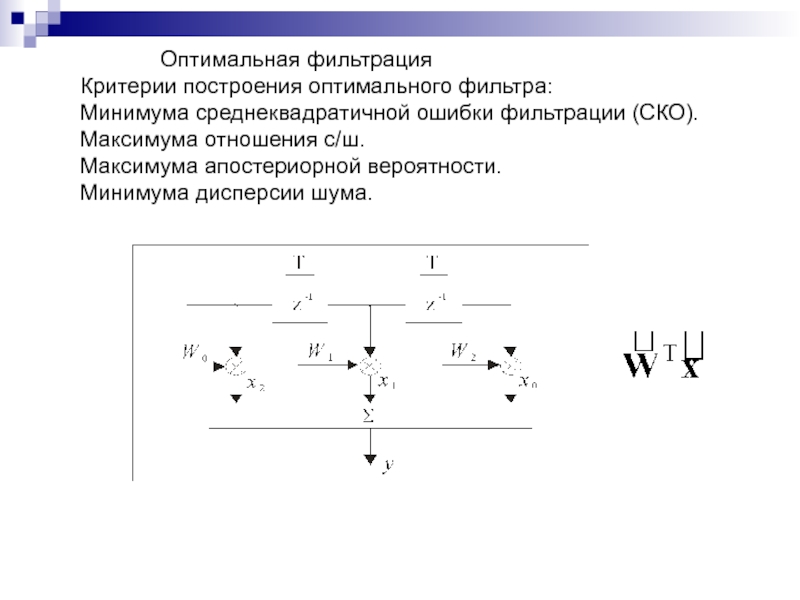
Слайд 20 Оптимальная фильтрация
Критерии построения оптимального фильтра:
Минимума среднеквадратичной ошибки фильтрации (СКО).
Максимума отношения с/ш.
Максимума
Минимума дисперсии шума.