электропроводность. Теплопроводность. Закон Видемана-Франца. Эффект Холла, постоянная Холла. Теплоемкость. Теория металлов Зоммерфельда.
Уравнение Шредингера для свободных электронов. Граничное условие Борна-Кармана. Характеристики фермиевских электронов для стандартного металла. Недостатки модели свободных электронов.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модель свободных электронов. Теория металлов Друде. Основные положения. Статическая электропроводность презентация
Содержание
- 1. Модель свободных электронов. Теория металлов Друде. Основные положения. Статическая электропроводность
- 2. Модель свободных электронов Теория металлов Друде
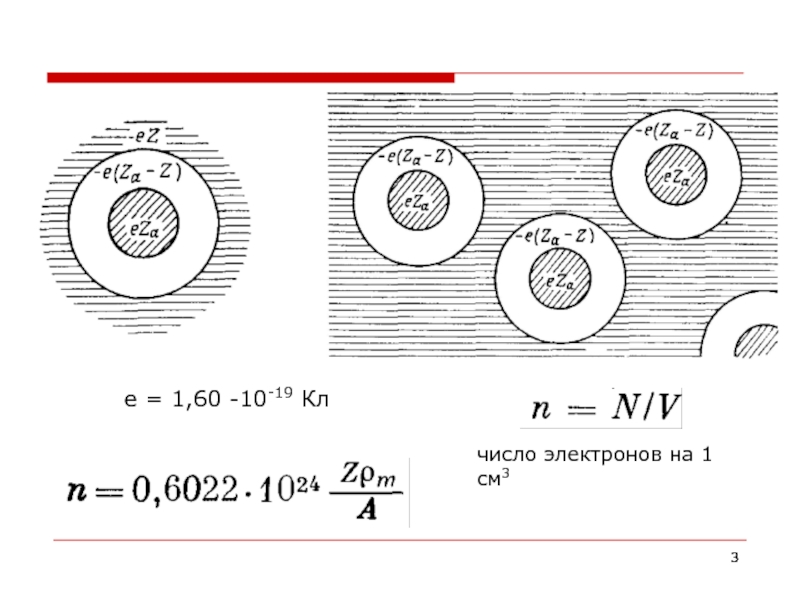
- 3. е = 1,60 -10-19 Кл число электронов на 1 см3
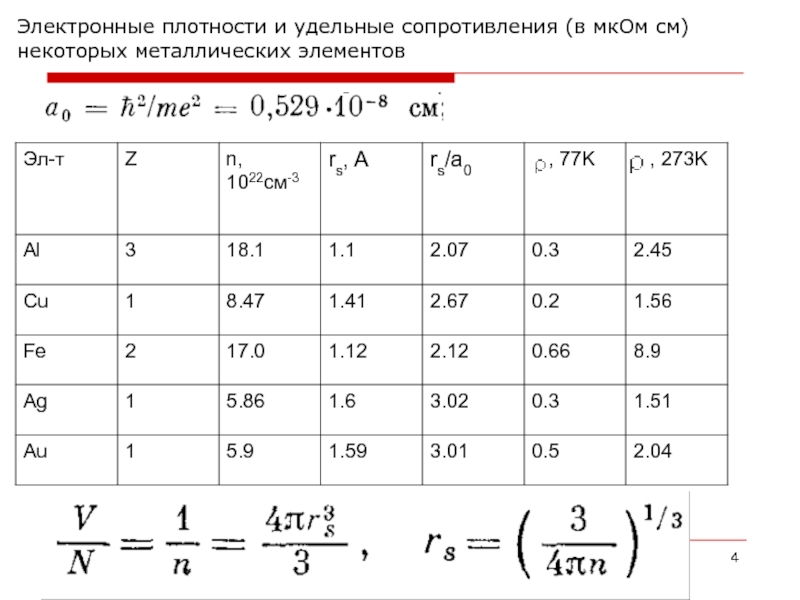
- 4. Электронные плотности и удельные сопротивления (в мкОм см) некоторых металлических элементов
- 5. Статическая электропроводность металлов Плотность тока j
- 6. dv/dt = -eE/m, средняя скорость vср = -eE/m
- 8. v0 (107 см/с) Оценки ℓ
- 9. В каждый момент времени t средняя скорость
- 10. Электроны, не испытавшие столкновений в интервале t
- 11. Это уравнение означает-- эффект столкновений отдельных электронов
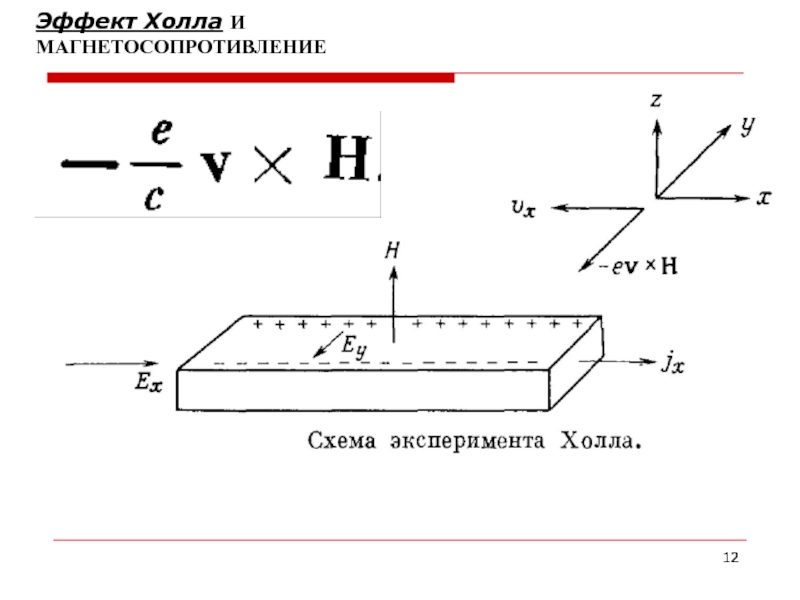
- 12. Эффект Холла И МАГНЕТОСОПРОТИВЛЕНИЕ
- 13. Коэффициент Холла измерения поля Холла позволяют
- 14. X имеется электрическое поле с произвольными компонентами
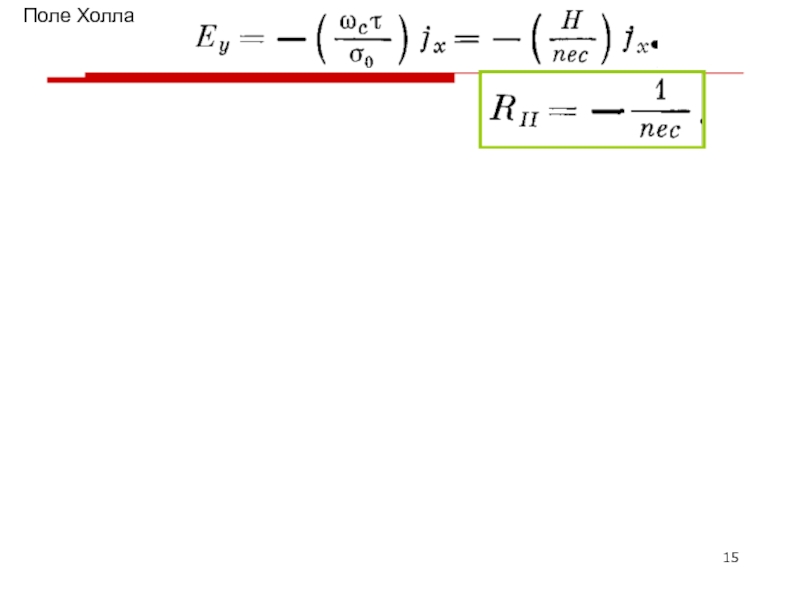
- 15. Поле Холла
- 16. в действительности эти коэффициенты обычно зависят от
- 17. безразмерная величина ωCτ Когда
- 18. Закон Видемана-Франца (1853). Теплопроводность металлов. Экспериментальные
- 20. В соответствии с законом Фурье поток тепла
- 21. (n/2) (-υ) ε(Т [х + υτ]) -
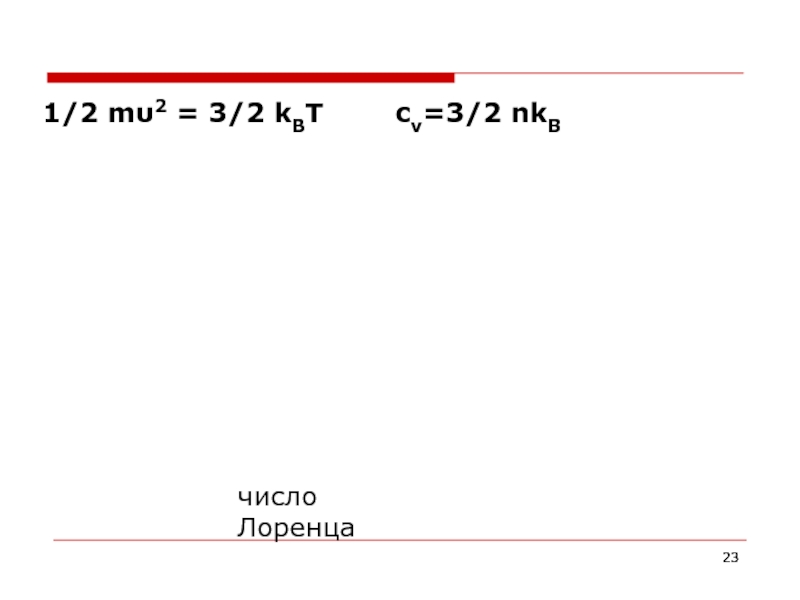
- 23. 1/2 mυ2 = 3/2 kBT сv=3/2 nkB число Лоренца
- 24. Термодинамическое состояние макросистемы
- 25. квантование фазового пространства
- 26. Число элементарных фазовых ячеек в шаровом слое
- 28. Зависимость плотности числа квантовых состояний от энергии свободной микрочастицы f- функция распределения
- 29. Невырожденные и вырожденные системы частиц условие невырожденности N/G ~1 вырожденные
- 30. n =1026 м –3 ; m =4,5•10–26
- 31. Квантовые распределения распределения представляют собой функции ,
- 36. Электроны возбуждаются на более высокие уровни при Т>0 они заняты
- 37. распределение Бозе–Эйнштейна
- 38. 8,617 3324(78)·10−5 эВ/К
- 39. классическое распределение Больцмана справедливо лишь тогда, когда малы «числа заполнения» фазовых ячеек,— при условии
- 40. Теория металлов Зоммерфельда (1928г) – квантовая модель газа свободных и независимых электронов Ферми.
- 42. СВОЙСТВА ЭЛЕКТРОННОГО ГАЗА В ОСНОВНОМ СОСТОЯНИИ
- 44. Допустимым волновым функциям соответствуют только определенные точки k- пространства
- 47. число разрешенных значений k в единице объема в k-пространстве (плотность уровней в k-пространстве)
- 48. импульс Ферми энергия скорость Ферми n
- 49. радиус сферы, объем которой равен объему, приходящемуся
- 51. делим на
- 53. Оценки из теории Зоммерфельда -Термодинамические свойства электронного газа
- 59. -Средняя длина пробега ≈ 102Å
- 60. Теплопроводность >
Модель свободных электронов Теория металлов Друде Основные положения: 1) Газ независимых электронов. В интервалах между столкновениями не учитывается взаимодействие электронов с другими электронами и ионами. В отсутствие электромагнитных
Слайд 2Модель свободных электронов
Теория металлов Друде
Основные положения:
1) Газ независимых электронов.
В интервалах между столкновениями не учитывается взаимодействие электронов с другими электронами и ионами. В отсутствие электромагнитных внешних полей электрон движется по прямой с постоянной скоростью до очередного столкновения.
2) Столкновения - мгновенные события, внезапно меняющие скорость электронов.
3) В единицу времени электрон испытывает столкновение с вероятностью W~1/t . За время dt - W ~ dt/ t.
t- время релаксации, не зависит от пространственного положения электрона и его скорости.
4) Электрон приходит в состояние теплового равновесия со своим окружением исключительно благодаря столкновениям.
Слайд 5Статическая электропроводность металлов
Плотность тока j - вектор, параллельный потоку заряда;
его величина равна количеству заряда, проходящему за единицу времени через единичную площадку, перпендикулярную потоку.
+
Слайд 9В каждый момент времени t средняя скорость электронов v равна р
(t)/m, где р — средний импульс, т. е. полный импульс, приходящийся на один электрон.
t ---? р (t)
Вычислим р (t+dt)
с момента времени t до t + dt – вероятность испытать столкновение dt/τ,
вероятность без столкновений - (1 - dt/τ).
Если электрон не испытывает столкновений---? сила f (t)
приобретет дополнительный импульс - f (t) dt +0 (dt2).
Плотность тока
Слайд 10Электроны, не испытавшие столкновений в интервале t и t+dt --? t+dt
(1 — dt/τ) * (р (t) + f (t) dt + 0 (dt2)).
Поправка за счет электронов, испытавших столкновение в интервале от
t до t +dt ≈0 (dt2).
Поправка за счет электронов, испытавших столкновение в интервале от
t до t +dt ≈0 (dt2).
Пренебрегаем вкладом в р (t + dt) от тех электронов, которые испытали столкновение за время между t и t + dt
Слайд 11Это уравнение означает-- эффект столкновений отдельных электронов сводится к введению в
уравнение движения для импульса, приходящегося на один электрон, дополнительного слагаемого, описывающего затухание за счет трения.
Слайд 13Коэффициент
Холла
измерения поля Холла позволяют определить знак носителей заряда
величина (магнитосопротивление) не
зависит от поля
Слайд 14X
имеется электрическое поле с произвольными компонентами Ех и Еy, а также
магнитное поле Н, направленное вдоль оси z. На каждый электрон действует (не зависящая от пространст-венных координат)
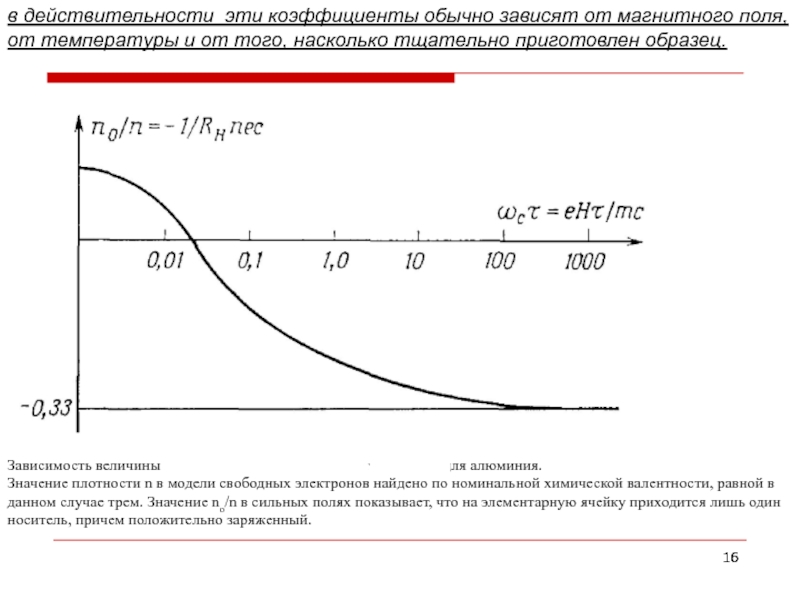
Слайд 16в действительности эти коэффициенты обычно зависят от магнитного поля, от температуры
и от того, насколько тщательно приготовлен образец.
Зависимость величины от для алюминия.
Значение плотности n в модели свободных электронов найдено по номинальной химической валентности, равной в данном случае трем. Значение nо/n в сильных полях показывает, что на элементарную ячейку приходится лишь один носитель, причем положительно заряженный.
Слайд 17безразмерная величина ωCτ
Когда величина ωCτ мала ток j почти
параллелен Е, как это было бы в отсутствие магнитного поля.
В общем случае ток j направлен к Е под углом ϕ (называемым углом Холла). Из уравнений следует, что tg ϕ = ωCτ .
Величина ωC, называемая циклотронной частотой, представляет собой круговую частоту вращения свободного электрона в магнитном поле Н.
Произведение ωCτ мало, если электроны между столкновениями могут проделать лишь малую часть оборота, и велико, если они могут совершить много оборотов.
когда ωCτ << 1, магнитное поле лишь слегка деформирует орбиты электронов, а когда величина ωCτ сравнима с единицей и больше, то влияние магнитного поля на орбиты электронов становится преобладающим.
В общем случае ток j направлен к Е под углом ϕ (называемым углом Холла). Из уравнений следует, что tg ϕ = ωCτ .
Величина ωC, называемая циклотронной частотой, представляет собой круговую частоту вращения свободного электрона в магнитном поле Н.
Произведение ωCτ мало, если электроны между столкновениями могут проделать лишь малую часть оборота, и велико, если они могут совершить много оборотов.
когда ωCτ << 1, магнитное поле лишь слегка деформирует орбиты электронов, а когда величина ωCτ сравнима с единицей и больше, то влияние магнитного поля на орбиты электронов становится преобладающим.
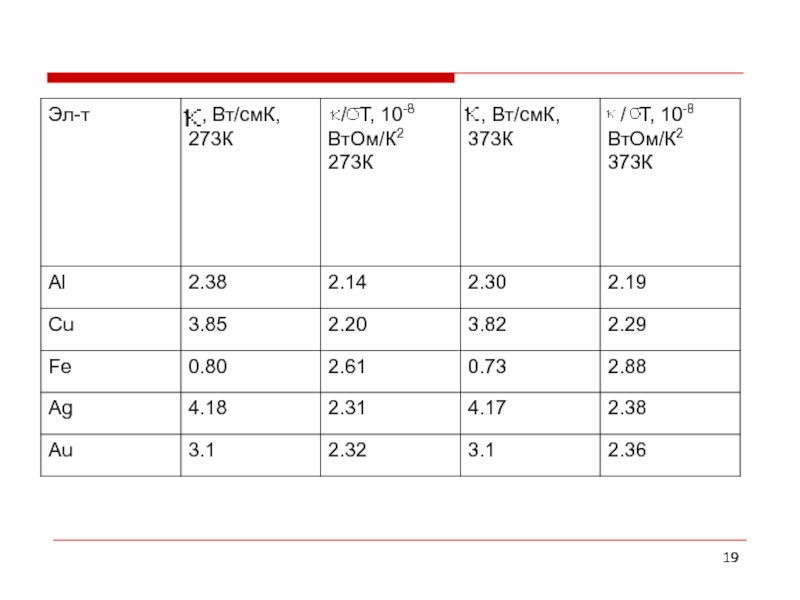
Слайд 18Закон Видемана-Франца (1853). Теплопроводность металлов.
Экспериментальные значения коэффициента теплопроводности и
числа
Лоренца
отношение κ/σ теплопроводности к электропроводности для большинства металлов прямо пропорционально температуре, причем коэффициент пропорциональности с достаточной точностью одинаков для всех металлов.
Слайд 20В соответствии с законом Фурье поток тепла пропорционален (и противоположно направлен)
градиенту температуры
коэффициент теплопроводности
ε(Т) — тепловая энергия в расчете на один электрон в металле, который находится в равновесии при температуре Т
ε(Т [х']) - тепловая энергия электрона, последнее столкновение которого
произошло в точке х’ (в среднем )
ε(Т [х — υτ])- тепловая энергия электрона, приходящего в точку х с той
стороны, где температура выше
(n/2) υ ε(Т [х — υτ])- вклад в плотность теплового потока
-
+
x
Слайд 21(n/2) (-υ) ε(Т [х + υτ]) -
вклад электронов, приходящих в точку
х с той стороны, где температура ниже
Слайд 26Число элементарных фазовых ячеек в шаровом слое
Шаровой слой в трехмерном пространстве
импульсов микрочастицы
g(p) — функция плотности квантовых состояний
Слайд 28Зависимость плотности числа квантовых состояний от энергии
свободной микрочастицы
f- функция распределения
Слайд 30n =1026 м –3 ; m =4,5•10–26 кг; kB T =
4•10–21 Дж
n = 5•1028 м –3 ; m = 9•10 –31 кг
T >105 K
Слайд 31Квантовые распределения
распределения представляют собой функции , определяющие средние числа частиц в
одной фазовой ячейке с энергией , или функции заполнения ячеек:
распределение Ферми–Дирака
Слайд 39
классическое распределение Больцмана справедливо лишь тогда, когда малы «числа заполнения» фазовых
ячеек,— при условии
Слайд 40Теория металлов Зоммерфельда (1928г) –
квантовая модель газа свободных и независимых электронов
Ферми.
Слайд 47число разрешенных значений k в единице объема в k-пространстве (плотность уровней
в k-пространстве)
Слайд 49радиус сферы, объем которой равен объему, приходящемуся на один электрон проводимости
для плотностей, соответствующих металлическим элементам
