- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы определения вязкости жидкости презентация
Содержание
- 1. Методы определения вязкости жидкости
- 2. Определение вязкости биологических жидкостей и, особенно, вязкости
- 3. а) Метод Стокса (метод падающего шарика)
- 4. Если в этой жидкости падает шарик радиусом
- 5. Согласно закону Стокса, сила сопротивления движению шарика
- 6. При достижении равномерного движения сила тяжести становится
- 7. Скорость движения шарика v определяется экспериментально. Для
- 8. Метод Стокса обладает хорошей точностью, однако, для
- 9. б) Капиллярные методы Капиллярные методы,
- 10. Представим U - образную трубку. В одном
- 11. Пусть вначале вискозиметр заполнен эталонной жидкостью, вязкость
- 12. Объем вытекшей воды равен:
- 13. Определив время истечения воды tо, заполним вискозиметр
- 14. Затем измеряем время t истечения объема исследуемой
- 15. Приравнивая правые части уравнений для объема вытекшей
- 16. Для определения вязкости проб крови может быть
- 17. в) Ротационные методы Достоинством этих методов
- 18. Рассмотрим принцип устройства одного из них. Представим
- 19. За счет вязкости жидкости при вращении наружного
- 20. При разных значениях скорости ω в жидкости,
- 21. Условия перехода ламинарного течения жидкости в турбулентное
- 22. Характер течения жидкости - ламинарный или турбулентный
- 23. Оказывается, что некоторая комбинация этих величин -
- 24. Если число Рейнольдса не превышает некоторого критического
- 25. Значение критического числа Рейнольдса можно определить экспериментально.
- 26. Допустим, что труба прозрачна и переход течения
- 27. Если Reкр известно, то становится возможным для
- 28. Пример. Вода течет по трубе диаметром d
- 29. Из образовавшегося уравнения: 2300 = v⋅103⋅2⋅10-3/10-3
Слайд 2 Определение вязкости биологических жидкостей и, особенно, вязкости крови имеет существенное диагностическое
Существуют следующие методы определения вязкости жидкости:
а) Метод Стокса (метод падающего шарика).
б) Капиллярные методы
в) Ротационные методы
Слайд 3
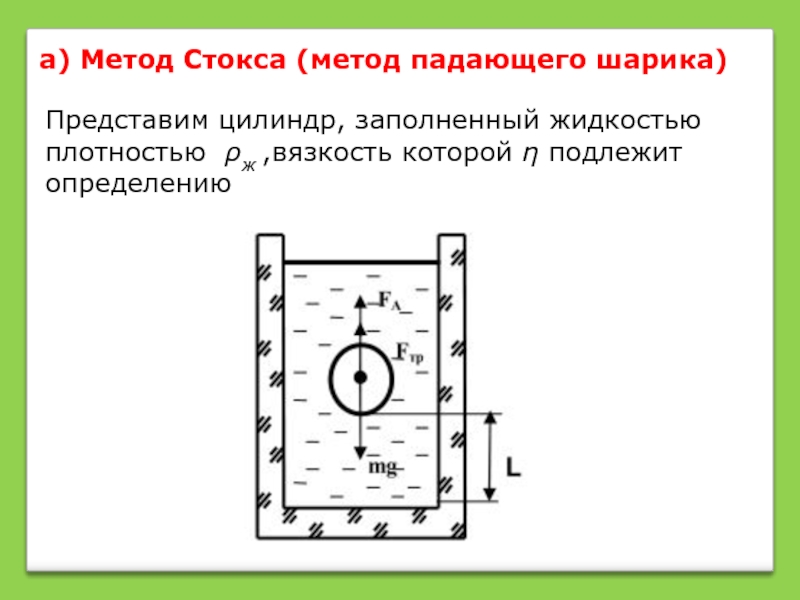
а) Метод Стокса (метод падающего шарика)
Представим цилиндр, заполненный жидкостью плотностью
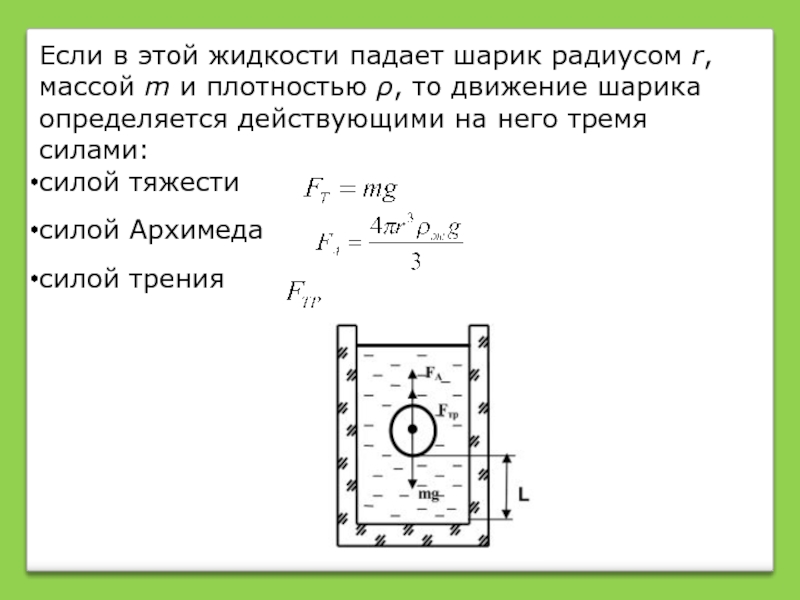
Слайд 4Если в этой жидкости падает шарик радиусом r, массой m и
силой тяжести
силой Архимеда
силой трения
Слайд 5 Согласно закону Стокса, сила сопротивления движению шарика FTP пропорциональна его радиусу,
Сила трения уменьшает скорость движения шарика и через некоторое время после погружения шарика в жидкость его движение может стать равномерным.
Слайд 6 При достижении равномерного движения сила тяжести становится равной сумме силы трения
Отсюда определим искомую вязкость:
Слайд 7Скорость движения шарика v определяется экспериментально. Для этого измеряется время t,
Слайд 8Метод Стокса обладает хорошей точностью, однако, для определения вязкости крови он
требует значительного количества исследуемой крови.
в жидкостях, обладающих не очень большой вязкостью, сложно удовлетворить требованию равномерности движения шарика.
Слайд 9б) Капиллярные методы
Капиллярные методы, основаны на применении формулы Пуазейля. Рассмотрим течение
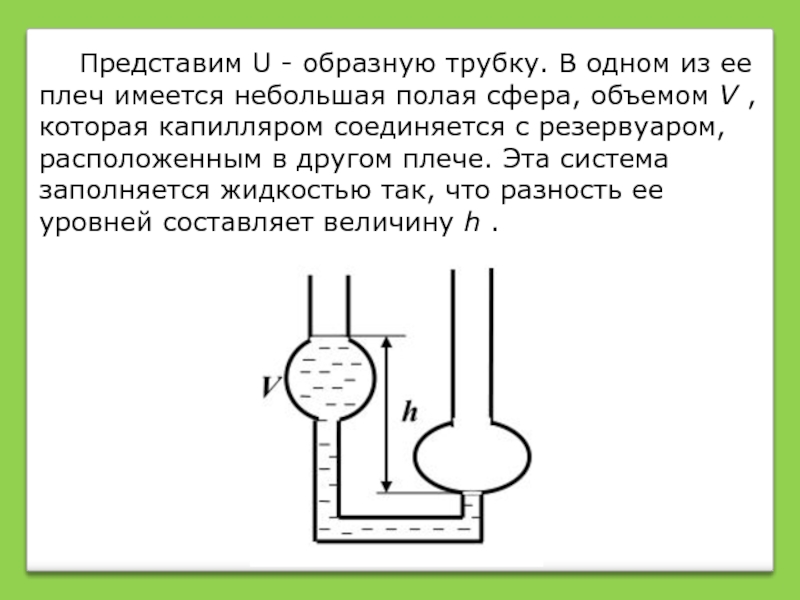
Слайд 10 Представим U - образную трубку. В одном из ее плеч имеется
Слайд 11 Пусть вначале вискозиметр заполнен эталонной жидкостью, вязкость которой точно известна. В
Поскольку при засасывании воды в левое плечо вискозиметра ее уровень здесь выше, чем в правом, то после прекращения всасывания жидкость будет перетекать через капилляр из левого плеча вискозиметра в правое до наступления равенства уровней. С помощью секундомера легко определить время tо, за которое вода вытекает из полости объемом V .
Слайд 12Объем вытекшей воды равен:
Где
ρо g h -разница давлений ,
ρо - плотность воды,
ηо - табличное значение вязкости воды при данной температуре.
Слайд 13 Определив время истечения воды tо, заполним вискозиметр исследуемой жидкостью, вязкость которой
При этом необходимо обеспечить такую же разность уровней жидкости h в плечах вискозиметра, что и при его заполнении водой.
Слайд 14 Затем измеряем время t истечения объема исследуемой жидкости V , который
где
η - вязкость исследуемой жидкости,
ρ - плотность исследуемой жидкости.
Слайд 15Приравнивая правые части уравнений для объема вытекшей и исследуемой жидкости
получим
Слайд 16 Для определения вязкости проб крови может быть использован вискозиметр Гесса, в
Слайд 17в) Ротационные методы
Достоинством этих методов является возможность определять не только значение
Существуют разнообразные ротационные вискозиметры.
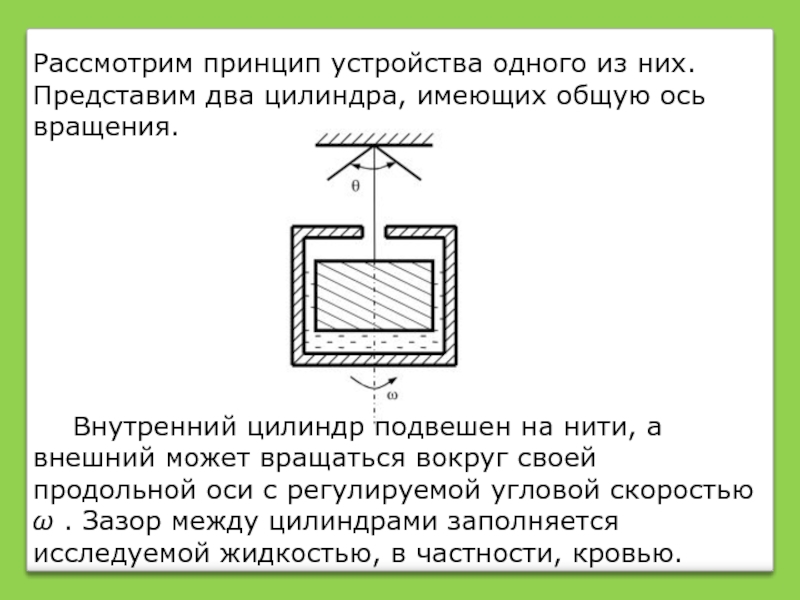
Слайд 18Рассмотрим принцип устройства одного из них. Представим два цилиндра, имеющих общую
Внутренний цилиндр подвешен на нити, а внешний может вращаться вокруг своей продольной оси с регулируемой угловой скоростью ω . Зазор между цилиндрами заполняется исследуемой жидкостью, в частности, кровью.
Слайд 19За счет вязкости жидкости при вращении наружного цилиндра внутренний цилиндр начинает
Этот угол можно легко измерить.
Чем больше вязкость жидкости и угловая скорость вращения ω, тем больше и указанный угол поворота:
= k η ω
где k - постоянная прибора.
Слайд 20 При разных значениях скорости ω в жидкости, заполняющей зазор между цилиндрами,
а в неньютоновских жидкостях эту зависимость можно не только наблюдать, но и определить количественно.
Таким образом, данные ротационной вискозиметрии позволяют судить об изменении вязкости движущейся крови при различных скоростях сдвига.
Слайд 22Характер течения жидкости - ламинарный или турбулентный – зависит:
от плотности
ее вязкости η ,
скорости течения v ,
диаметра трубы d, по которой течет жидкость.
Слайд 23 Оказывается, что некоторая комбинация этих величин - один безразмерный параметр -
Слайд 24Если число Рейнольдса не превышает некоторого критического значения Re < Reкр
Если же Re > Reкр , то в потоке жидкости возникают завихрения - ее течение становится турбулентным.
Слайд 25Значение критического числа Рейнольдса можно определить экспериментально.
Представим, что по гладкой
Плотность воды, ее вязкость и диаметр трубы известны.
Слайд 26Допустим, что труба прозрачна и переход течения жидкости из ламинарного в
Постепенно увеличивая скорость течения, отметим то ее значение vкр, при котором в потоке жидкости начинает проявляться турбулентность. Подставив это значение vкр в формулу
получим величину критического числа Рейнольдса. Для гладких труб
Reкр = 2300.
Слайд 27Если Reкр известно, то становится возможным для любой жидкости и разных
Слайд 28Пример. Вода течет по трубе диаметром d = 2 мм. При
Решение. Примем вязкость воды η = 10-3 Па⋅с, плотность ρ = 103 кг/м3 и подставим эти значения в правую часть формулы числа Рейнольдса. В левую часть подставим значение критического числа Рейнольдса.
Слайд 29Из образовавшегося уравнения:
2300 = v⋅103⋅2⋅10-3/10-3
найдем, что течение воды в
v = 1,15 м/с
С увеличением диаметра трубы и уменьшением вязкости жидкости переход из ламинарного течения в турбулентное наступает при уменьшающихся значениях скорости.