- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механизмы уширения линий. Теория излучения. (Тема 12) презентация
Содержание
- 1. Механизмы уширения линий. Теория излучения. (Тема 12)
- 2. Естественное затухание излучения Тепловое уширение линий
- 3. Два подхода в теории излучения В теории
- 4. Фотоны являются синусиодаль- ными вариациями электромагнит- ного
- 5. Коэффициент поглощения ν-ν0 есть расстояние от
- 6. Вид коэффициента поглощения с естественным уширением
- 7. Естественное затухание (квантовая
- 8. Сила осциллятора (1) Получим интегральный коэффициент поглощения,
- 9. Сила осциллятора (2) Сила осциллятора есть число
- 10. Сила осциллятора (3) Силы осцилляторов определяются
- 11. Yширение линий эффектом Допплера (1)
- 12. Yширение эффектом Допплера (2) 1) Допплер эффект
- 13. Число частиц N с определенными
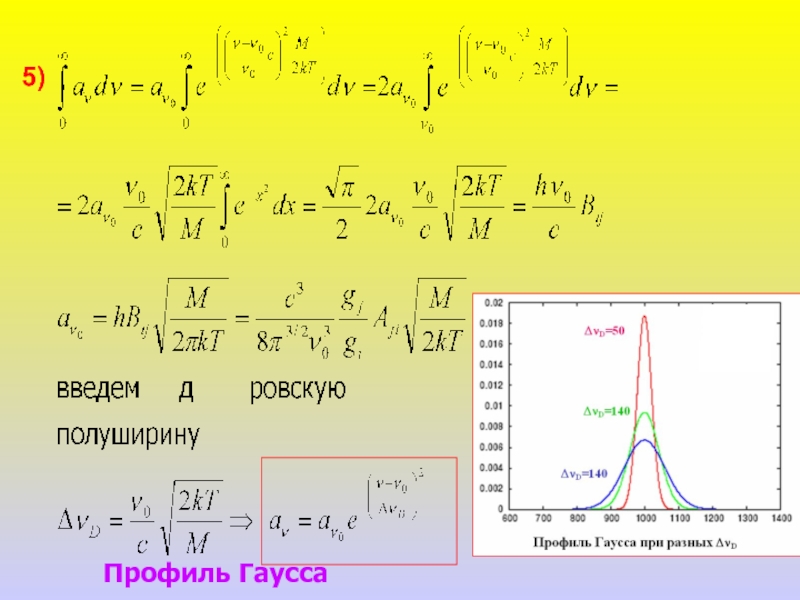
- 14. 4)
- 15. 5) Профиль Гаусса
- 16. Оценка роли Доплер-эффекта 1. Полуширина –
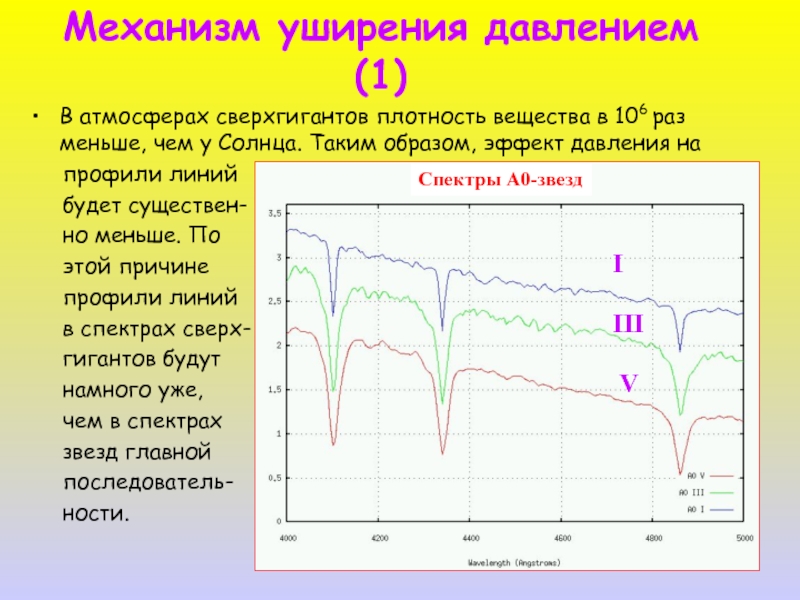
- 18. Механизм уширения давлением (1) В атмосферах сверхгигантов
- 19. Механизм уширения давлением (2) Ударное уширение происходит,
- 20. Варианты эффектов давления Прямые удары Прохождения около
- 21. Роль прямых ударов Ударяющая частица
- 22. Два подхода Ударное приближение: излучающий атом возмуща-
- 23. 1 подход – ударное приближение или
- 24. 1 подход – ударное приближение или метод
- 25. Учеты многих прохождений Теория показывает, что
- 26. Квазистатическое приближение В этой теории время возмущения
- 27. Статистическая теория (приближение ближайшей частицы)
- 29. Эффект Штарка (первое приближение)
- 30. Основные предположения: возмущающие частицы – ионы ионы
- 31. Резюме:
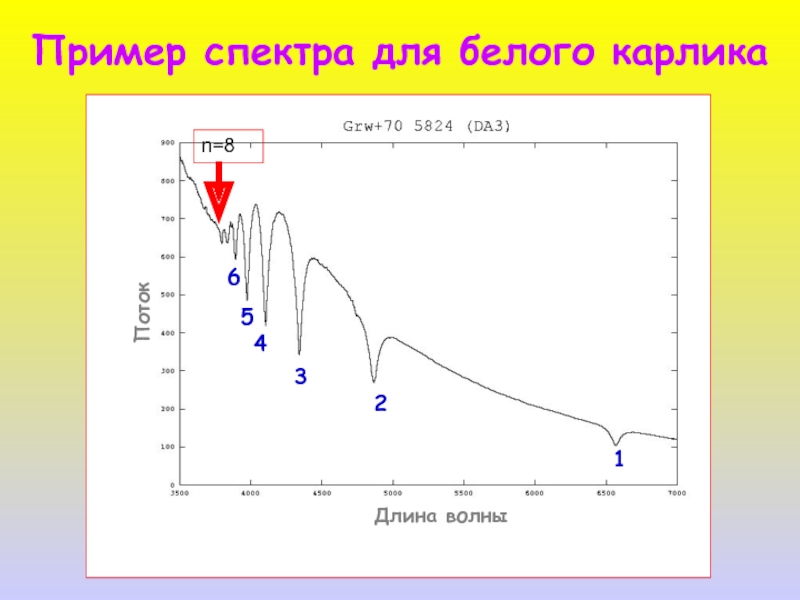
- 32. Формула Инглиса-Теллера
- 33. n=8 Пример спектра для белого карлика 1
- 35. Совместное влияние всех трех механизмов (1)
- 36. Совместное влияние всех трех механизмов (2)
- 37. Профиль Фойгта Свертка двух функций : дисперсионной
- 38. Частные случаи: В центре линии
- 39. Вычисление функции Фойгта Функция Хьертинга хорошо изучена
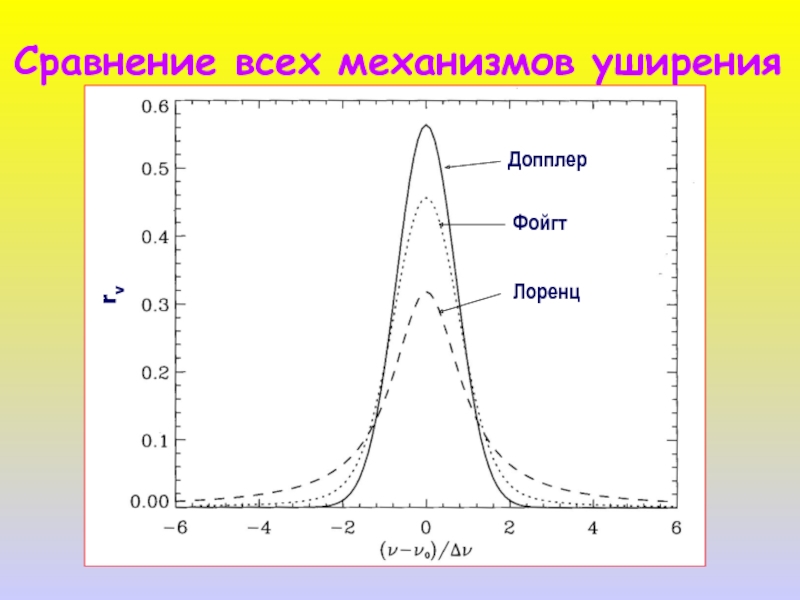
- 40. Сравнение всех механизмов уширения Допплер
- 41. Рабочие формулы для оценки роли механизмов уширения
- 42. Рабочие формулы для оценки роли механизмов
Слайд 2Естественное затухание излучения
Тепловое уширение линий из-за хаотического кинетического движения атомов
Уширение
Сверхтонкая структура
Эффект Зеемана (в магнитном поле)
Механизмы уширения линий
Слайд 3Два подхода в теории излучения
В теории излучения используются два подхода –
Классическая физика: электромагнитное поле это непрерывная функция и в пространстве и времени с хорошо известными значениями электрического и магнитного полей.
Квантовая механика: поле излучения это
ансамбль дискретных квантов энергии hν.
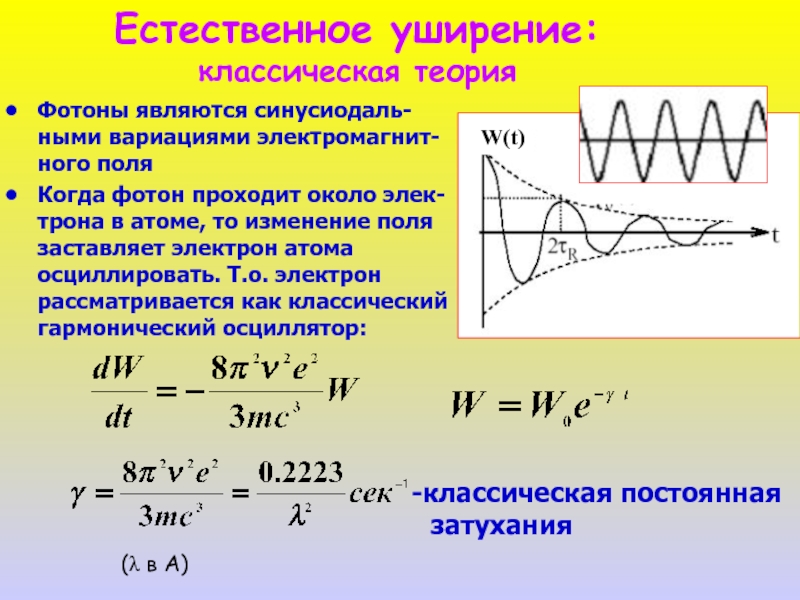
Слайд 4Фотоны являются синусиодаль- ными вариациями электромагнит- ного поля
Когда фотон проходит около
(λ в А)
классическая постоянная
затухания
Естественное уширение:
классическая теория
W(t)
Слайд 5Коэффициент поглощения
ν-ν0 есть расстояние от центра линии
γ −
Часто записанное выше выражение называется профилем Лоренца, так как выражение
называется функцией Лоренца. Иногда такой профиль называют дисперсионным
Слайд 6Вид коэффициента поглощения с
естественным уширением
Полуширина линии будет на расстоянии
В шкале
Полуширина очень мала для всех линий!
Полуширина линии
Слайд 7 Естественное затухание
(квантовая теория излучения)
Принцип неопределенностей
Гейзенберга
Замена γ
Уширение зависит от времени жизни атома на уровне
Постоянная уширения γ для резонансных линий по значению близка к классической постоянной.
Постоянная затухания для других линий может превышать классическое значение в 5-50 раз
Слайд 8Сила осциллятора (1)
Получим интегральный коэффициент поглощения, используя
классическую теорию:
Аналогичную операцию произведем для
щения из квантовой теории излучения:
В результате можно убедиться, что . Чтобы
согласовать классическую теорию с квантовомеханической
теорией вводят «силу осциллятора» f:
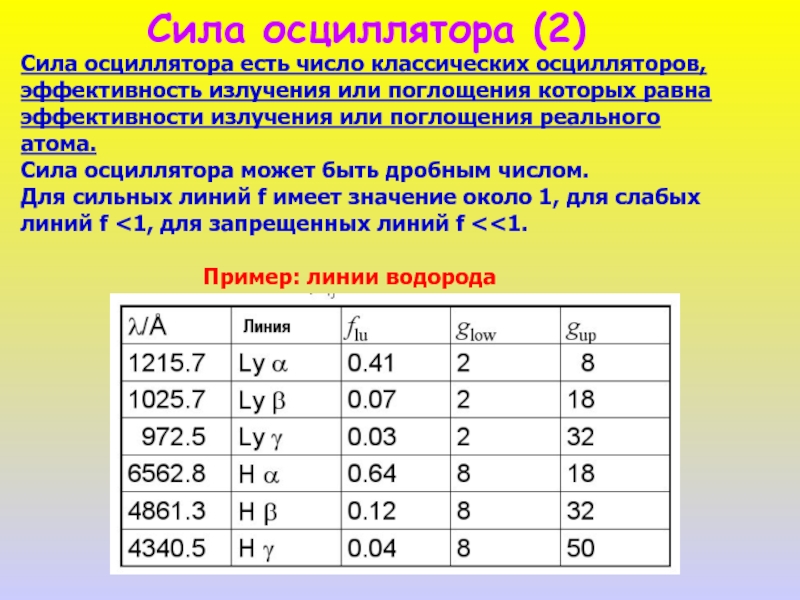
Слайд 9Сила осциллятора (2)
Сила осциллятора есть число классических осцилляторов,
эффективность излучения или
эффективности излучения или поглощения реального
атома.
Сила осциллятора может быть дробным числом.
Для сильных линий f имеет значение около 1, для слабых
линий f <1, для запрещенных линий f <<1.
Пример: линии водорода
Слайд 10Сила осциллятора (3)
Силы осцилляторов определяются одним из методов:
-
- лабораторные измерения,
- по измерениям интенсивностей линий в
солнечном спектре
Слайд 12Yширение эффектом Допплера (2)
1) Допплер эффект уширяет линию за счет следующих
Тепловое уширение( из-за движения частиц)
Уширение турбулентностью (мико/макро)
2) Уширение пропорционально числу частиц
с определенными скоростями, т.е.
Поглощающие атомы находятся в движении. Проекция скорости
движения на луч зрения Vr вызывает смещение частоты: квант в системе координат, связанной с атомом, поглощает (излучает) в частоте ν, но наблюдатель фиксирует частоту ν’.
ν
ν’
наблюдатель
Слайд 13
Число частиц N с определенными
скоростями (распределение Максвелла) при разных Tc
Скорость (cм/сек)
3)
Слайд 16Оценка роли Доплер-эффекта
1. Полуширина – расстояние от центра линии Δλ1/2,
рой коэффициент поглощения падает в два раза по отношению
к его максимальному значению:
2. Полуширина - расстояние от центра линии ΔλD, при кото-
рой коэффициент поглощения падает в e раз по отношению
к его максимальному значению.
Пример:
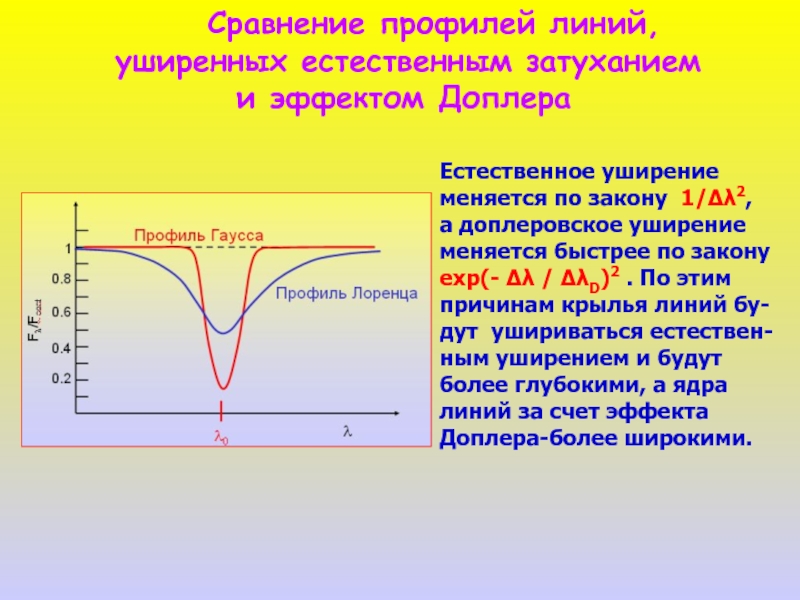
Слайд 17
уширенных естественным затуханием
и эффектом Доплера
Естественное уширение
меняется по закону 1/Δλ2,
а доплеровское уширение
меняется быстрее по закону
exp(- Δλ / ΔλD)2 . По этим
причинам крылья линий бу-
дут ушириваться естествен-
ным уширением и будут
более глубокими, а ядра
линий за счет эффекта
Доплера-более широкими.
Слайд 18Механизм уширения давлением (1)
В атмосферах сверхгигантов плотность вещества в 106 раз
профили линий
будет существен-
но меньше. По
этой причине
профили линий
в спектрах сверх-
гигантов будут
намного уже,
чем в спектрах
звезд главной
последователь-
ности.
Спектры А0-звезд
I
III
V
Слайд 19Механизм уширения давлением (2)
Ударное уширение происходит, когда
поглощающий или
сталкивается с атомами, ионами и
электронами или проходит близко к ним.
2. Таким образом, этот эффект зависит от
плотности вещества (и температуры).
Эти эффекты могут играть роль в широком
диапазоне физических условий: от газовых
туманностей до черных дыр.
4. В результате ударов или прохождений
энергетические уровни слегка размываются,
тем самым увеличивая диапазон длин волн
поглощения в линии – линия уширяется.
Слайд 20Варианты эффектов давления
Прямые удары
Прохождения около атомов другого рода
Эффект собственного давления –
Возмущения статическим электрическим полем ионов (Stark-эффект)
Слайд 21Роль прямых ударов
Ударяющая частица может привести к ударному девозбуждению
Теория дает следующую формулу для полуширины в зависимости от давления (P=NkT):
Для Солнца (T=5800K, P=104) для атома водорода прямые удары при σ=πa02=8x10-21 м2 вызывают уширение с
Эта величина меньше естественного уширения!
Слайд 22Два подхода
Ударное приближение: излучающий атом возмуща- ется проходящими частицами на расстоянии
Квазистатическое приближение: это приближение используется, когда t>>t0. Поэтому в первом приближении частицы можно считать неподвижными.
Слайд 23
1 подход – ударное приближение или метод дискретных встреч(МДВ)
Предполагается, что прохождения
частицы
мгновенно. В результате цуг
волн мгновенно меняет свою
фазу (см. рисунок). Смещение
по частоте представляется как
Слайд 241 подход – ударное приближение или метод дискретных встреч(МДВ)
Этот метод
Естественно полагать, что смещение по частоте
r-2 – возмущение статическим полем ионов и/или электронов (линейный Штарк-эффект). Это уширение особенно важно для линий HI в спектрах горячих звезд.
r-3 - резонансное уширение атомами того же рода. Это уширение важно в атмосферах холодных звезд, например, линии HI в спектре Солнц.
r-4 – если возмущаемый атом имеет внутренние электроны (квадратичный Штарк-эффект). Уширение важно для линий ионов металлов в спектрах горячих звезд.
r-6 - уширение Ван дер Ваальса нейтральными атомами. Уширение важно в спектрах холодных звезд.
Слайд 25Учеты многих прохождений
Теория показывает, что зависимость коэффициента поглощения имеет такой же
Ударное уширение имеет вид дисперсионной функции
Иногда Γcoll превышает Γrad в 10 раз
Слайд 26Квазистатическое приближение
В этой теории время возмущения атома со стороны
других частиц
возбужденном состоянии. Время t остается
практически постоянным во время процесса
поглощения или излучения кванта в статистически
флуктуирующем поле, создаваемом другими части-
цами.
Теория строится на следующей цепочке:
Распределение возмущающих частиц силовое
поле в месте расположения поглощающего или
излучающего атома переход от распределения
возмущающих частиц к частотному распределению
(коэффициенту поглощения).
Слайд 27Статистическая теория (приближение
ближайшей частицы)
r
dr
Вероятность расположения W( r ) ближайшей частицы
-вероятности W1 того, что в сфере радиусом r частицы нет
-вероятности W2 того, что внутри cфери- ческого слоя (r,r+dr) частица есть.
W1
W2
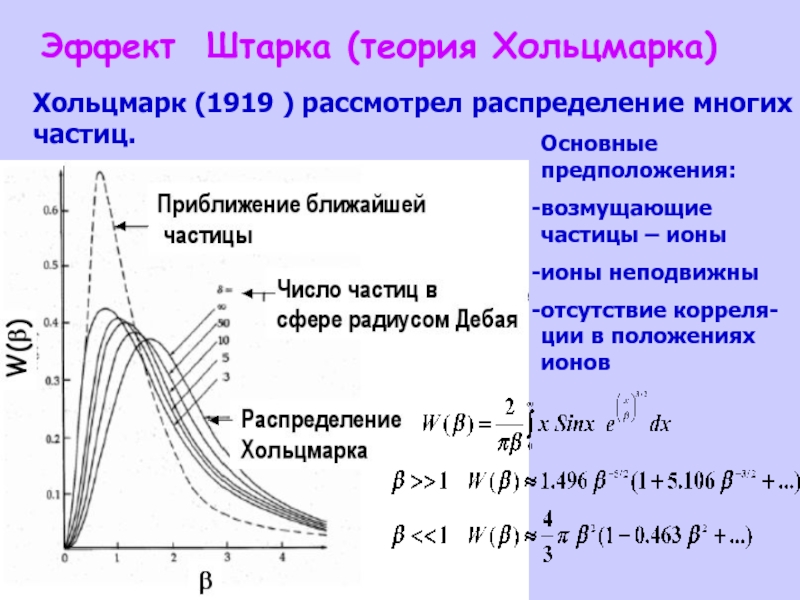
Слайд 29 Эффект Штарка (первое приближение)
Приближение ближайшей частицы:
- среднее расстояние
- «нормальная» напряженность электрического поля
- определим
- переводим
Слайд 30Основные предположения:
возмущающие частицы – ионы
ионы неподвижны
отсутствие корреля- ции в положениях ионов
Эффект
Хольцмарк (1919 ) рассмотрел распределение многих
частиц.
Слайд 35Совместное влияние
всех трех механизмов (1)
Совместный учет всех механизмов уширения это
конволюция всех коэффициентов:
Первые три профиля являются дисперсионными
Конволюция первых трех (лоренцовских) профилей
дает также лоренцовский профиль
Квадратичный Штарк эффект Силы Ван дер Ваальсф
Естественное затухание Линейный Штарк-эффект
Слайд 36Совместное влияние
всех трех механизмов (2)
Конволюция профиля Лоренца и профиля Гаусса
дает более сложный профиль:
Слайд 37Профиль Фойгта
Свертка двух функций : дисперсионной и функции Гаусса дает новый
Часто вместо функции Хьертинга используют функцию Фойгта:
длина волны центра линии
Слайд 39Вычисление функции Фойгта
Функция Хьертинга хорошо изучена и протабулирована как функция двуъ
u=Δλ/ΔλD
a=(λ2/4πc)/ΔλD =(γ/4π)ΔνD
Часто ее представляют в виде ряда
H(a,u)=H0(u) + aH1(u) + a2H2(u) + a3H3(u) +…
or, the absorption coefficient is
Слайд 41Рабочие формулы для оценки
роли механизмов уширения (1)
Допплеровское уширение. Полуширина линии определя-
ется
Здесь масса атома дана в единицах атомной массы (AMU).
Резонансное уширение (эффекты давления такими же
частицами, что и излучающий (поглощающий) атом. Оно
имеет место для резонансных линий (переход на/c основной
уровень. Полуширина равна
-населенность основного уровня, - наблюдаемая
длина волны и длина волны резонансной линий
Слайд 42 Рабочие формулы для оценки
роли механизмов уширения (2)
Штарк эффект. Формула для
Параметр для линии водорода Hβ привелен в
таблице
T(K) 1015 1016 1017 1018
5 000 0.0787 0.0808 0.0765 ...
10 000 0.0803 0.0840 0.0851 0.0781
20 000 0.0815 0.0860 0.0902 0.0896
30 000 0.0814 0.0860 0.0919 0.0946
Ne
Аналогичные таблицы имеются и для других линий.
Естественное уширение.