- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механика жидкости и газа. Гидростатика презентация
Содержание
- 1. Механика жидкости и газа. Гидростатика
- 2. 1. ГИДРОСТАТИКА
- 3. 1. Гидростатика В гидростатике изучают законы равновесия
- 4. 1. Гидростатика Поверхностные силы в покоящейся жидкости
- 5. 1. Гидростатика Дифференциальное уравнение гидростатики:
- 6. Следовательно, 1. Гидростатика – главный вектор
- 7. 1. Гидростатика Центр давления D – точка
- 8. Заглубление центра давления 1. Гидростатика Координата
- 9. Задача 1. На плотину из бетона
- 10. Задача 1. Гидростатика
- 11. Задача 1. Гидростатика
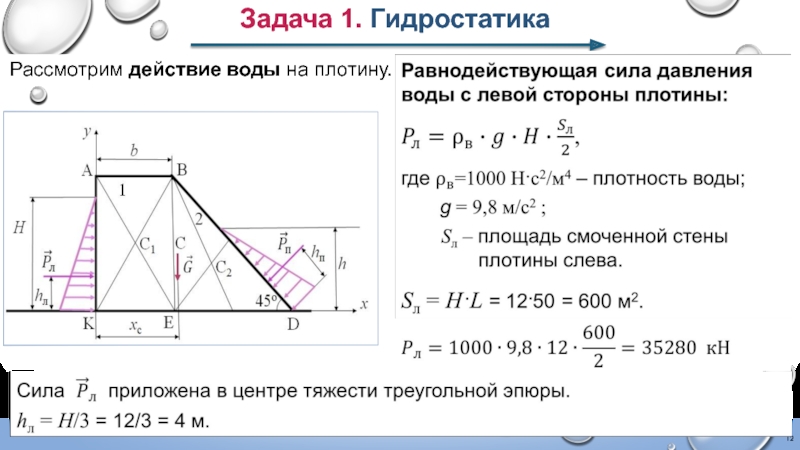
- 12. Задача 1. Гидростатика Рассмотрим действие воды на плотину.
- 13. Задача 1. Гидростатика Равнодействующая сила давления
- 14. Задача 1. Гидростатика Найдем центр тяжести
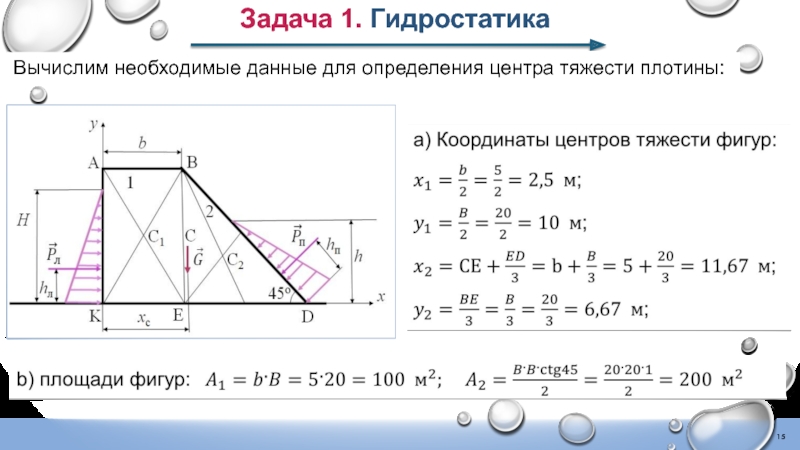
- 15. Задача 1. Гидростатика Вычислим необходимые данные для определения центра тяжести плотины:
- 16. Задача 1. Гидростатика
- 17. Задача 1. Гидростатика
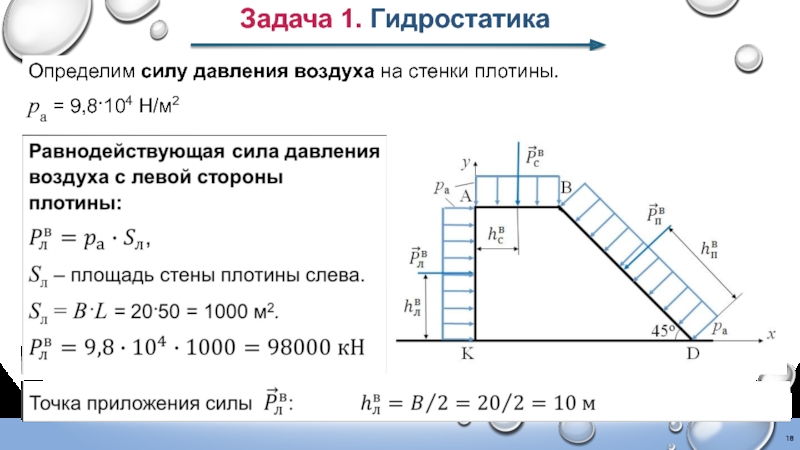
- 18. Задача 1. Гидростатика Определим силу
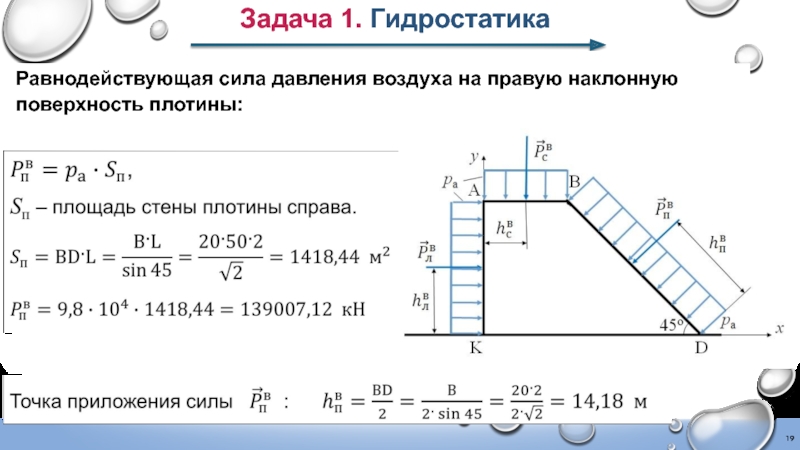
- 19. Задача 1. Гидростатика Равнодействующая сила давления воздуха на правую наклонную поверхность плотины:
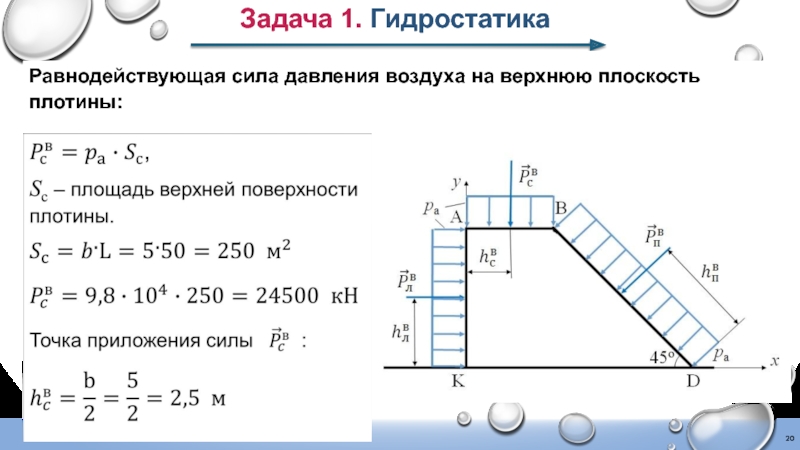
- 20. Задача 1. Гидростатика Равнодействующая сила давления воздуха на верхнюю плоскость плотины:
- 21. Задача 1. Гидростатика
- 22. Задача 1. Гидростатика
- 23. Задача 1. Гидростатика
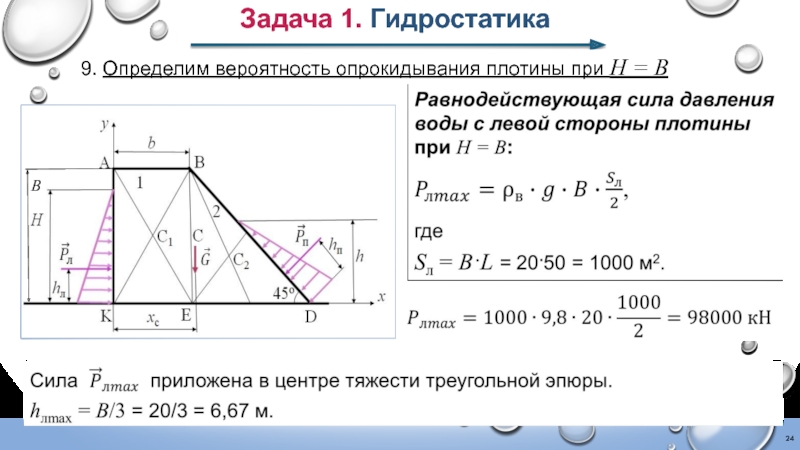
- 24. Задача 1. Гидростатика 9. Определим вероятность
- 25. Задача 1. Гидростатика
- 26. Задача 1. Гидростатика
- 27. 2. ДИНАМИКА ОДНОМЕРНЫХ ТЕЧЕНИЙ ЖИДКОСТИ И ГАЗА
- 28. 2.1. ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ОДНОМЕРНЫХ СТАЦИОНАРНЫХ ТЕЧЕНИЙ
- 29. 2.1. Основные уравнения динамики одномерных стационарных
- 30. 2.1. Основные уравнения динамики одномерных стационарных
- 31. 2.1. Основные уравнения динамики одномерных стационарных
- 32. 2.1. Основные уравнения динамики одномерных стационарных
- 33. 2.1. Основные уравнения динамики одномерных стационарных
- 34. 2.1. Основные уравнения динамики одномерных стационарных течений Уравнение Бернулли для идеальной жидкости:
- 35. 2.1. Основные уравнения динамики одномерных стационарных течений Уравнение Бернулли в единицах давления:
- 36. 2.1. Основные уравнения динамики одномерных стационарных
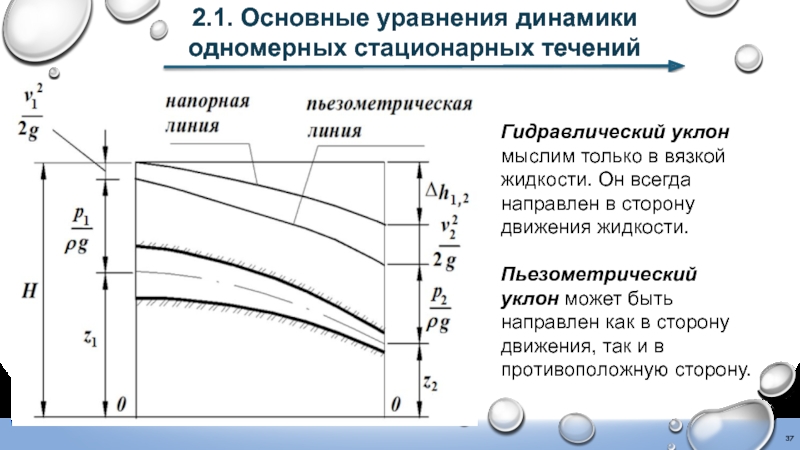
- 37. Гидравлический уклон мыслим только в вязкой жидкости.
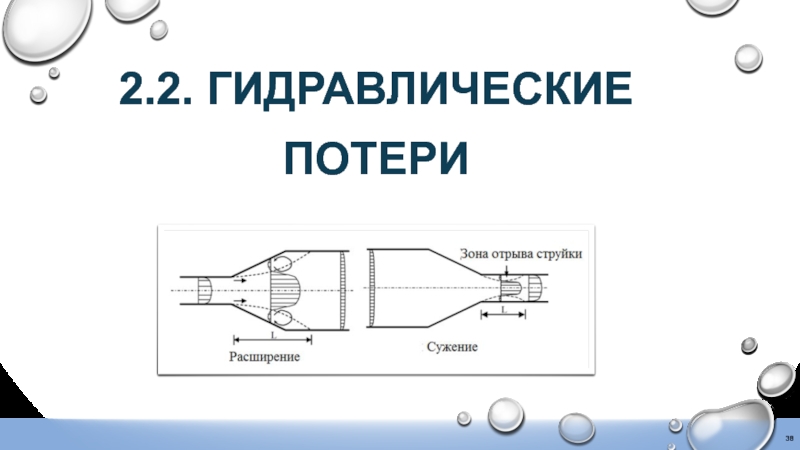
- 38. 2.2. ГИДРАВЛИЧЕСКИЕ ПОТЕРИ
- 39. 2.2. Гидравлические потери Потери при одномерном течении:
- 40. 2.2. Гидравлические потери Переход от ламинарного к
- 41. 2.2. Гидравлические потери
- 42. 2.2. Гидравлические потери Коэффициент гидравлического трения:
- 43. 2.2. Гидравлические потери Средняя шероховатость (высота бугорков стенок) трубы (мм) Таблица 1.
- 44. 2.2. Гидравлические потери
- 45. 2.2. Гидравлические потери Коэффициенты потерь для некоторых местных сопротивлений Таблица 2.
- 46. 2.2. Гидравлические потери Коэффициенты потерь для некоторых местных сопротивлений Продолжение таблицы 2.
- 47. 2.2. Гидравлические потери Коэффициенты потерь для некоторых местных сопротивлений Продолжение таблицы 2.
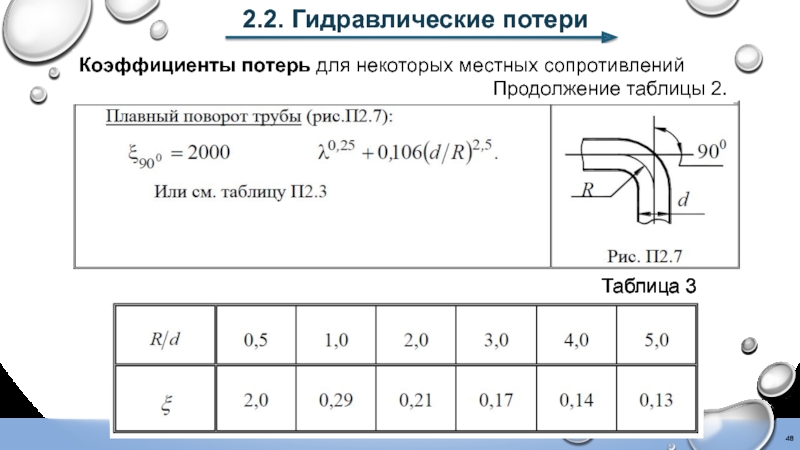
- 48. 2.2. Гидравлические потери Коэффициенты потерь для некоторых местных сопротивлений Продолжение таблицы 2. Таблица 3
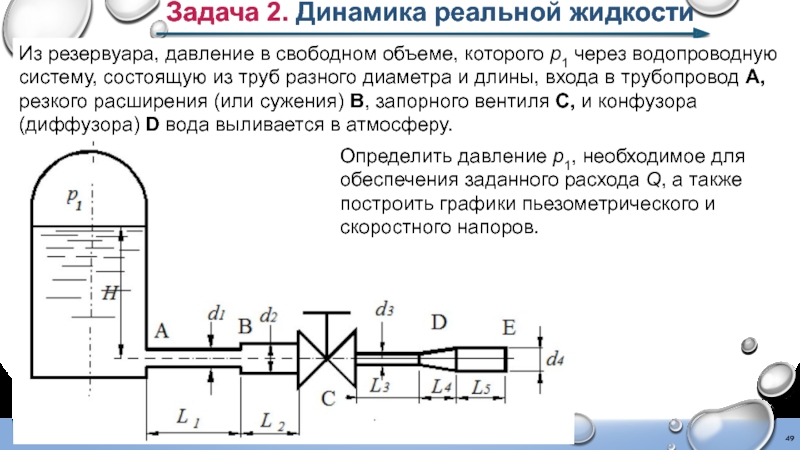
- 49. Задача 2. Динамика реальной жидкости Из резервуара,
- 50. Задача 2. Динамика реальной жидкости Дано:
- 51. Задача 2. Динамика реальной жидкости Составим уравнение
- 52. Задача 2. Динамика реальной жидкости
- 53. Задача 2. Динамика реальной жидкости Тогда уравнение
- 54. Число Рейнольдса: Задача 2. Динамика реальной жидкости
- 55. Это турбулентный режим, поэтому коэффициент гидравлического
- 56. Это область гидравлических гладких труб, поэтому коэффициент
- 57. Найдем потери напора
- 58. Задача 2. Динамика реальной жидкости Найдем местные
- 59. Коэффициент сопротивления при прохождении через вентиль
- 60. Задача 2. Динамика реальной жидкости Найдем α
- 61. Потери напора на выход из трубы в
- 62. Находим высоту, обусловленную избыточным давлением в резервуаре
- 63. Задача 2. Динамика реальной жидкости Напорная и
- 64. Задача 2. Динамика реальной жидкости Напорная и пьезометрическая линии
- 65. 3. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДКОВ
- 66. 3. Истечение жидкости из отверстий и насадков
- 67. 3. Истечение жидкости из отверстий и насадков
- 68. 3. Истечение жидкости из отверстий и насадков
- 69. 3. Истечение жидкости из отверстий и насадков
- 70. 3. Истечение жидкости из отверстий и насадков
- 71. 3. Истечение жидкости из отверстий и насадков
- 72. 3. Истечение жидкости из отверстий и насадков
- 73. Задача 3. Истечение жидкости из отверстий и
- 74. Задача 3. Истечение жидкости из отверстий и
- 75. Задача 3. Истечение жидкости из отверстий и
- 76. Задача 3. Истечение жидкости из отверстий и
Слайд 31. Гидростатика
В гидростатике изучают законы равновесия жидкости и газа
и их
Силы, действующие в сплошной среде, делят на 2 группы:
распределенные по объему – массовые силы,
распределенные по поверхности – поверхностные силы.
Слайд 41. Гидростатика
Поверхностные силы в покоящейся жидкости – силы, направленные по нормали
Давление представляет собой физический скаляр.
Единица гидростатического давления - паскаль: 1Па =1Н/м2
Единицы измерения давления в технике:
атмосфера: 1атм = 98066,5 Па ≈ 100 кПа,
миллиметр ртутного столба: 1мм.рт.ст. =98066,5 Па/760 = 129 Па.
Слайд 51. Гидростатика
Дифференциальное уравнение гидростатики:
где - плотность жидкости, ось
Слайд 6Следовательно,
1. Гидростатика
– главный вектор сил давления жидкости
на
– давление в центре тяжести
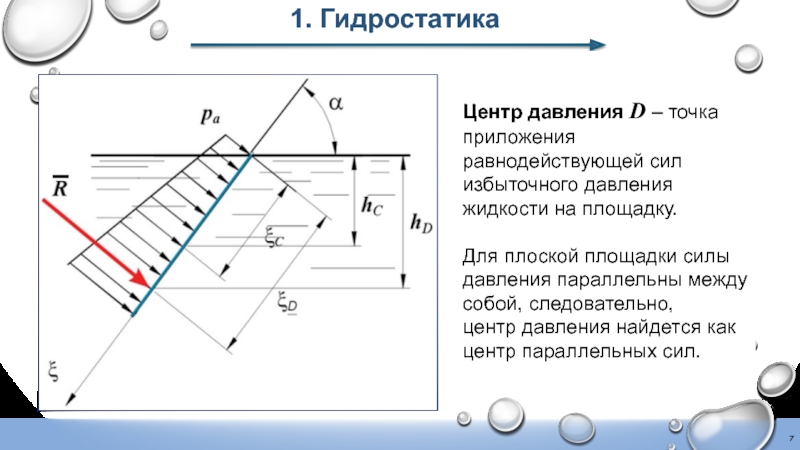
Слайд 71. Гидростатика
Центр давления D – точка приложения равнодействующей сил избыточного давления
Для плоской площадки силы давления параллельны между собой, следовательно,
центр давления найдется как центр параллельных сил.
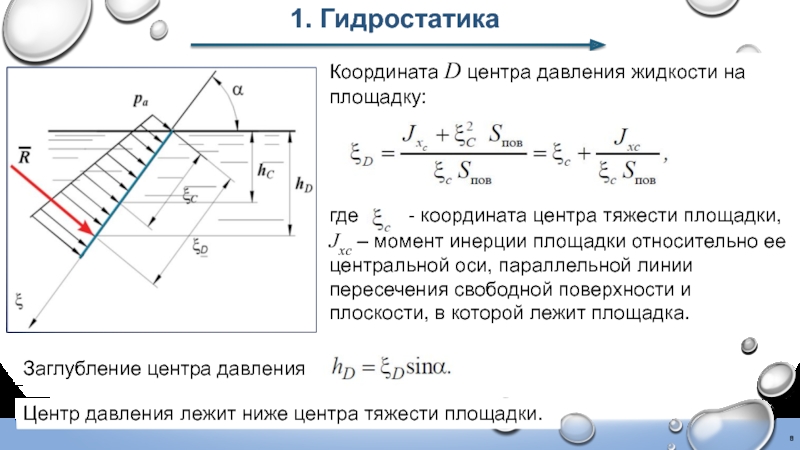
Слайд 8Заглубление центра давления
1. Гидростатика
Координата D центра давления жидкости на площадку:
где - координата центра тяжести площадки,
Jxс – момент инерции площадки относительно ее центральной оси, параллельной линии пересечения свободной поверхности и плоскости, в которой лежит площадка.
Центр давления лежит ниже центра тяжести площадки.
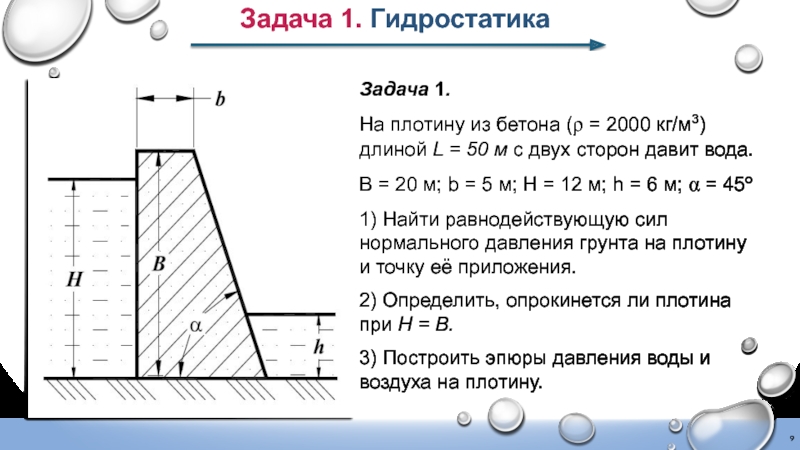
Слайд 9Задача 1.
На плотину из бетона (ρ = 2000 кг/м3) длиной
В = 20 м; b = 5 м; H = 12 м; h = 6 м; α = 45о
1) Найти равнодействующую сил нормального давления грунта на плотину и точку её приложения.
2) Определить, опрокинется ли плотина при Н = В.
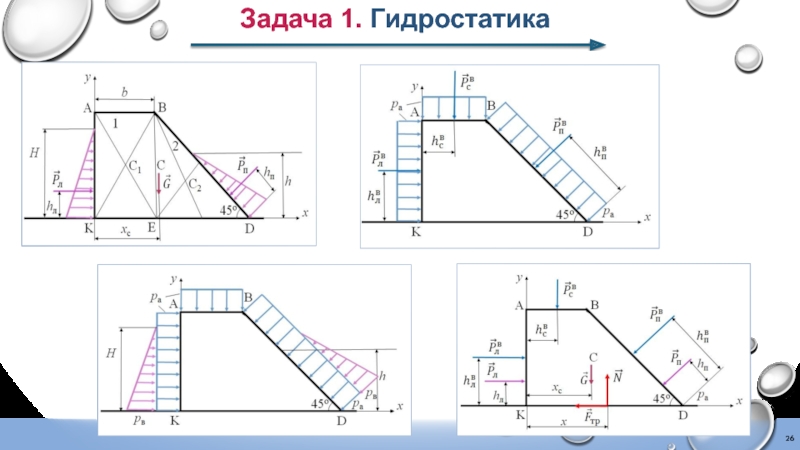
3) Построить эпюры давления воды и воздуха на плотину.
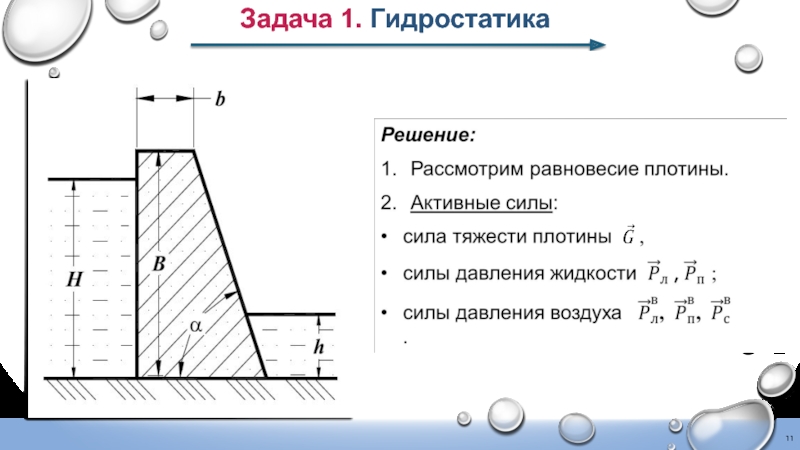
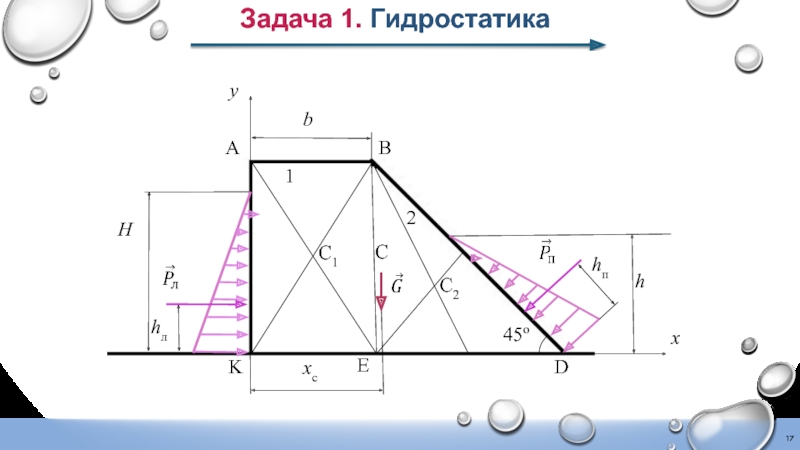
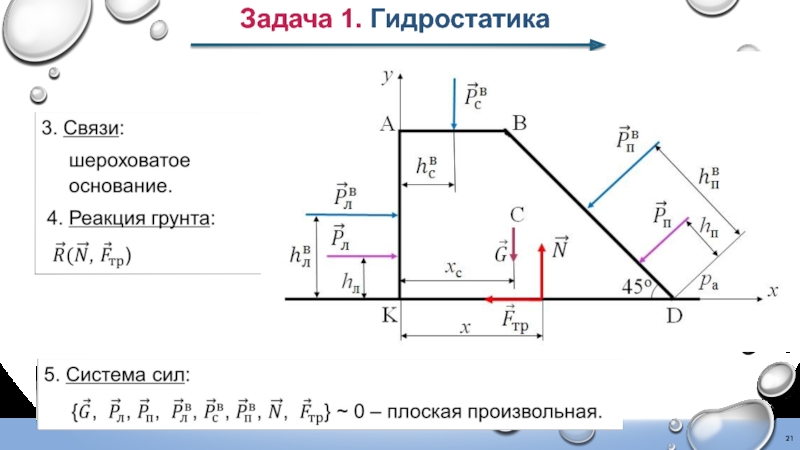
Задача 1. Гидростатика
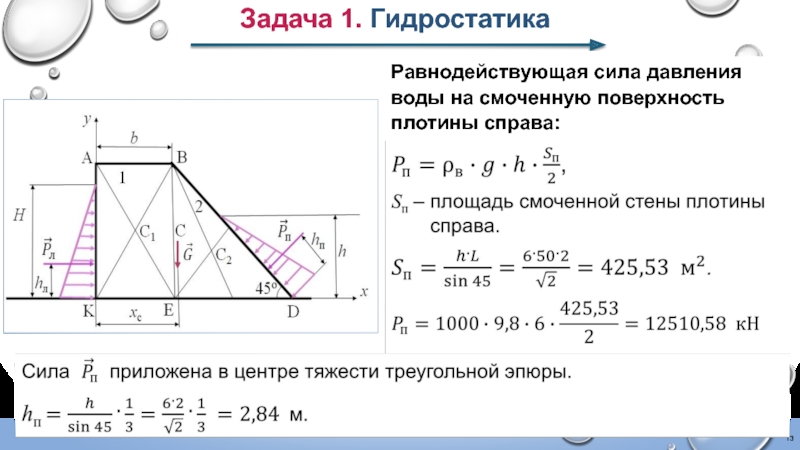
Слайд 13Задача 1. Гидростатика
Равнодействующая сила давления воды на смоченную поверхность
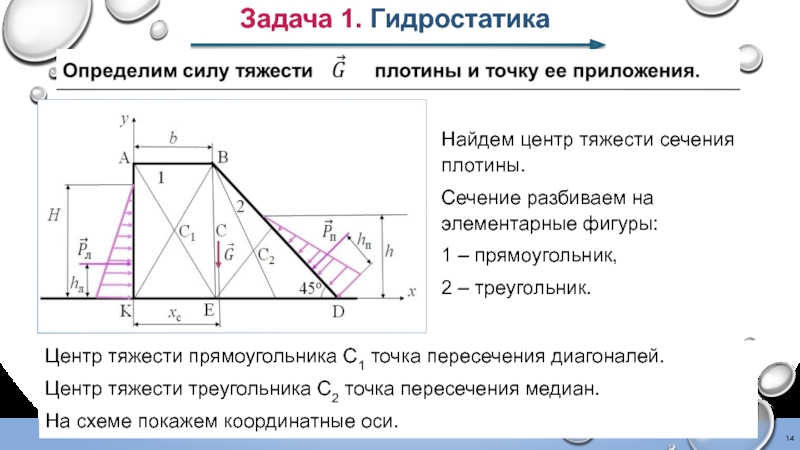
Слайд 14Задача 1. Гидростатика
Найдем центр тяжести сечения плотины.
Сечение разбиваем на элементарные
1 – прямоугольник,
2 – треугольник.
Центр тяжести прямоугольника С1 точка пересечения диагоналей.
Центр тяжести треугольника С2 точка пересечения медиан.
На схеме покажем координатные оси.
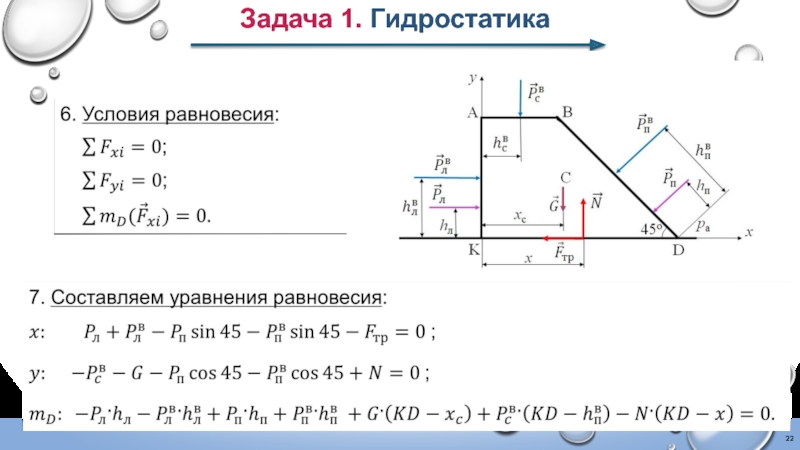
Слайд 19Задача 1. Гидростатика
Равнодействующая сила давления воздуха на правую наклонную поверхность
Слайд 25Задача 1. Гидростатика
Момент, препятствующий опрокидыванию:
Так как опрокидывающий момент значительно меньше
Слайд 292.1. Основные уравнения динамики
одномерных стационарных течений
К одномерным течениям относят такое
Слайд 302.1. Основные уравнения динамики
одномерных стационарных течений
Характеристики поперечного сечения потока:
смоченный
гидравлический диаметр DГ – отношение учетверенной площади нормального сечения к смоченному периметру:
Гидравлический диаметр заполненной жидкостью трубы круглого
сечения равен диаметру этой трубы.
гидравлический радиус:
Слайд 312.1. Основные уравнения динамики
одномерных стационарных течений
Уравнение неразрывности вырождается в уравнение
При одномерном установившемся движении основные уравнения гидродинамики могут быть существенно упрощены.
Слайд 322.1. Основные уравнения динамики
одномерных стационарных течений
Уравнение количества движения принимает вид
Слайд 332.1. Основные уравнения динамики
одномерных стационарных течений
Коэффициент α (коэффициент Кориолиса) представляет
Для равномерных течений α = 1.
Δh12 – удельная мощность внутренних сил на участке 1–2, или потеря полного
напора (гидравлические потери).
Слайд 342.1. Основные уравнения динамики
одномерных стационарных течений
Уравнение Бернулли для идеальной жидкости:
Слайд 352.1. Основные уравнения динамики
одномерных стационарных течений
Уравнение Бернулли в единицах давления:
Слайд 362.1. Основные уравнения динамики
одномерных стационарных течений
Пьезометрический и гидравлический уклоны положительные,
если
Слайд 37Гидравлический уклон мыслим только в вязкой жидкости. Он всегда направлен в
Пьезометрический уклон может быть направлен как в сторону движения, так и в противоположную сторону.
2.1. Основные уравнения динамики
одномерных стационарных течений
Слайд 392.2. Гидравлические потери
Потери при одномерном течении:
1) потери по длине;
Природа гидравлических сопротивлений достаточно сложна.
Они зависят от сил внутреннего и внешнего трения, от геометрии твердых границ. Их теоретическое исследование слишком сложно, поэтому на практике пользуются экспериментальными данными.
Гидравлические потери самым существенным образом зависят от режима течения жидкости.
Иначе потери полного напора называют гидравлическими сопротивлениями.
Режимы движения жидкости:
Ламинарный – режим, при котором частицы жидкости движутся слоями,
без перемешивания.
Турбулентный – режим с беспорядочным перемешиванием жидкости.
Слайд 402.2. Гидравлические потери
Переход от ламинарного к турбулентному режиму происходит при критическом
где v – средняя скорость, μ – коэффициент динамической вязкости,
d – характерный размер (гидравлический диаметр сечения)
Размерность коэффициента вязкости:
динамического [μ] = Н·с/м2,
кинематического [ν] = [μ /ρ] = м2/c.
Слайд 432.2. Гидравлические потери
Средняя шероховатость (высота бугорков стенок) трубы (мм)
Таблица 1.
Слайд 452.2. Гидравлические потери
Коэффициенты потерь для некоторых местных сопротивлений
Таблица 2.
Слайд 462.2. Гидравлические потери
Коэффициенты потерь для некоторых местных сопротивлений
Продолжение таблицы 2.
Слайд 472.2. Гидравлические потери
Коэффициенты потерь для некоторых местных сопротивлений
Продолжение таблицы 2.
Слайд 482.2. Гидравлические потери
Коэффициенты потерь для некоторых местных сопротивлений
Продолжение таблицы 2.
Таблица
Слайд 49Задача 2. Динамика реальной жидкости
Из резервуара, давление в свободном объеме, которого
Определить давление p1, необходимое для обеспечения заданного расхода Q, а также построить графики пьезометрического и скоростного напоров.
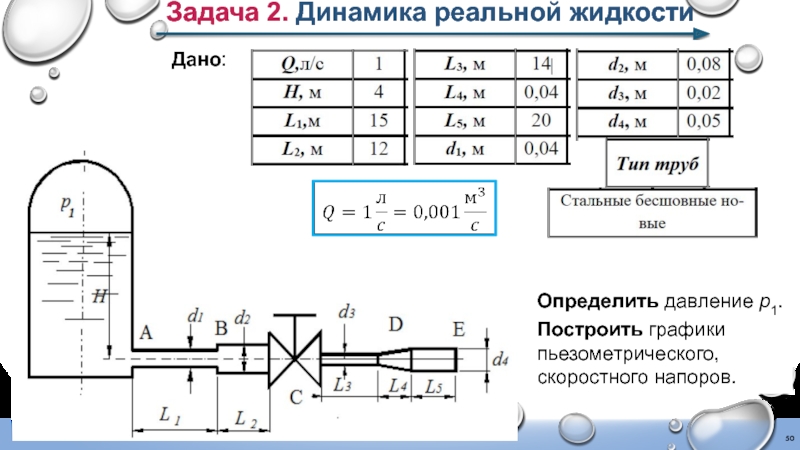
Слайд 50Задача 2. Динамика реальной жидкости
Дано:
Определить давление p1.
Построить графики пьезометрического,
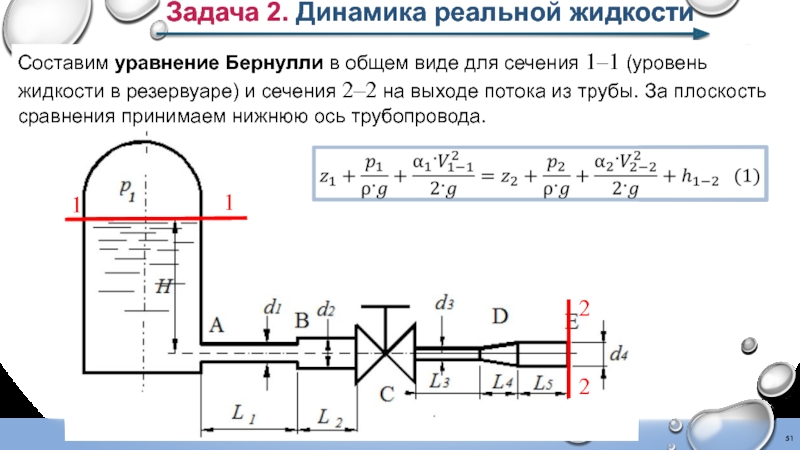
Слайд 51Задача 2. Динамика реальной жидкости
Составим уравнение Бернулли в общем виде для
1
1
2
2
Слайд 53Задача 2. Динамика реальной жидкости
Тогда уравнение Бернулли принимает вид:
Потери напора равны
Потери напора по длине определяют по формуле Дарси:
Потери напора в местных сопротивлениях вычисляют по формуле Вейсбаха:
Слайд 54Число Рейнольдса:
Задача 2. Динамика реальной жидкости
Cкорости движения воды на каждом участке
c учетом постоянства расхода Q по формуле:
Определим режим движения жидкости на каждом участке .
Слайд 55Это турбулентный режим,
поэтому коэффициент гидравлического
трения определяем по формуле Альтшуля:
Задача
Для стальных бесшовных новых труб (по табл. П.2.1)δ = 0,014 мм = 0,014·10-3 м.
Для удобства вычислений диаметр перевели в мм: d1= 0,04 м = 40 мм.
Слайд 56Это область гидравлических гладких труб,
поэтому коэффициент гидравлического
трения определяем по формуле
Задача 2. Динамика реальной жидкости
Слайд 58Задача 2. Динамика реальной жидкости
Найдем местные потери напора по формуле Вейсбаха
Коэффициент сопротивления на входе в трубопровод (табл. П2.2): ξвх = 0,5
Коэффициент сопротивления на внезапное расширение (табл. П2.2):
Слайд 59
Коэффициент сопротивления при прохождении через вентиль (табл. П2.2):
ξвен = 4
Коэффициент сопротивления диффузора:
, где α – угол конусности
Задача 2. Динамика реальной жидкости
Слайд 61Потери напора на выход из трубы в атмосферу.
Коэффициент сопротивления на выходе
Общие потери напора:
Все скоростные напоры:
Задача 2. Динамика реальной жидкости
Слайд 62Находим высоту, обусловленную избыточным давлением в резервуаре hп:
В уравнение Бернулли (2)
и вычислим давление p1:
Задача 2. Динамика реальной жидкости
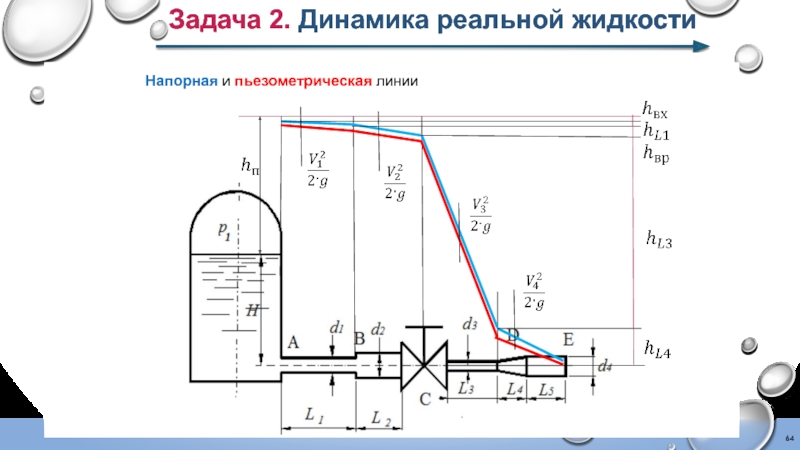
Слайд 63Задача 2. Динамика реальной жидкости
Напорная и пьезометрическая линии
Напорная линия показывает, как
При построении напорной линии значения высот (гидродинамических напоров) откладывают вертикально вверх от осевой линии трубопровода. По ходу движения напорная линия всегда падает, то есть имеет уклон, так как потери напора не обратимы.
Слайд 663. Истечение жидкости из отверстий и насадков
В гидравлике различают большие и
Отверстие называют малым, если его вертикальный размер
не превышает 0,1 напора.
где μ, φ – коэффициенты скорости и расхода, значения
которых приведены в таблице;
S – площадь отверстия;
H – геометрический напор над центром тяжести отверстия; p1 – давление на свободной поверхности жидкости;
p2 – давление в среде, в которую происходит истечение
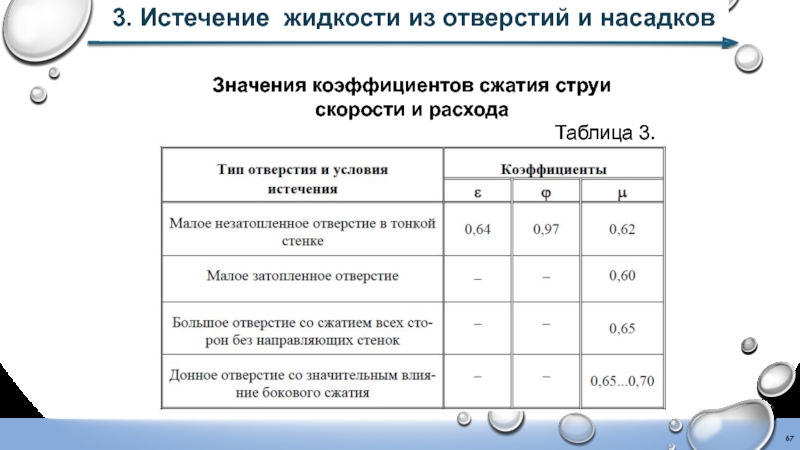
Слайд 673. Истечение жидкости из отверстий и насадков
Значения коэффициентов сжатия струи скорости
Таблица 3.
Слайд 683. Истечение жидкости из отверстий и насадков
Связь между коэффициентами μ и
где ε – коэффициент сжатия струи, равный отношению площади струи в сжатом сечении к площади отверстия.
Слайд 693. Истечение жидкости из отверстий и насадков
При истечении жидкости из открытого
(p1 = p2 = pа)
формулы для скорости v и расхода Q жидкости принимают простой вид:
Слайд 703. Истечение жидкости из отверстий и насадков
При истечении под уровень (в
где ΔH – разность уровней.
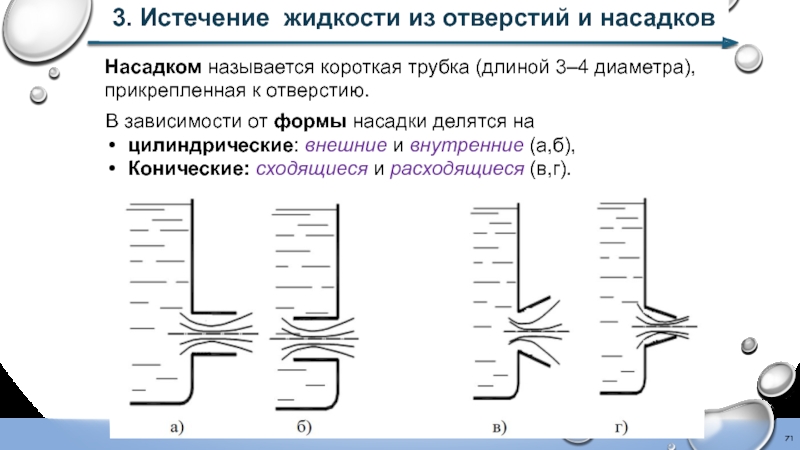
Слайд 713. Истечение жидкости из отверстий и насадков
Насадком называется короткая трубка (длиной
В зависимости от формы насадки делятся на
цилиндрические: внешние и внутренние (а,б),
Конические: сходящиеся и расходящиеся (в,г).
Слайд 723. Истечение жидкости из отверстий и насадков
Скорость и расход при истечении
Значения коэффициентов сжатия струи, скорости и расхода
Таблица 4.
Слайд 73Задача 3. Истечение жидкости из отверстий и насадков
Истечение воды из закрытого
а из открытого – через отверстие в тонкой стенке. Диаметры выходного отверстия насадка и отверстия в тонкой стенке одинаковы.
Определить расход воды через систему и избыточное давление p0 в закрытом резервуаре.
Дано:
Слайд 74Задача 3. Истечение жидкости из отверстий и насадков
d = 10 мм
Следовательно, отверстие является малым.
По таблице П3.1 для малого незатопленного отверстия принимаем коэффициент расхода μ0 = 0,62.
Расход жидкости при истечении из отверстия из открытого резервуара в атмосферу определяется по формуле:
(Для другой схемы для первого отверстия Н = Н2, для второго Н = Н3)
Слайд 75Задача 3. Истечение жидкости из отверстий и насадков
Расход из отверстия равен:
При