- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Магнитостатическое поле в вакууме. Часть 3 презентация
Содержание
- 1. Магнитостатическое поле в вакууме. Часть 3
- 2. Потенциальная энергия контура с
- 4. Положение контура соответствует минимуму его потенциальной энергии, т.е. состоянию устойчивого равновесия.
- 5. Контур с током в неоднородном поле
- 6. Пусть виток смещается в направлении на
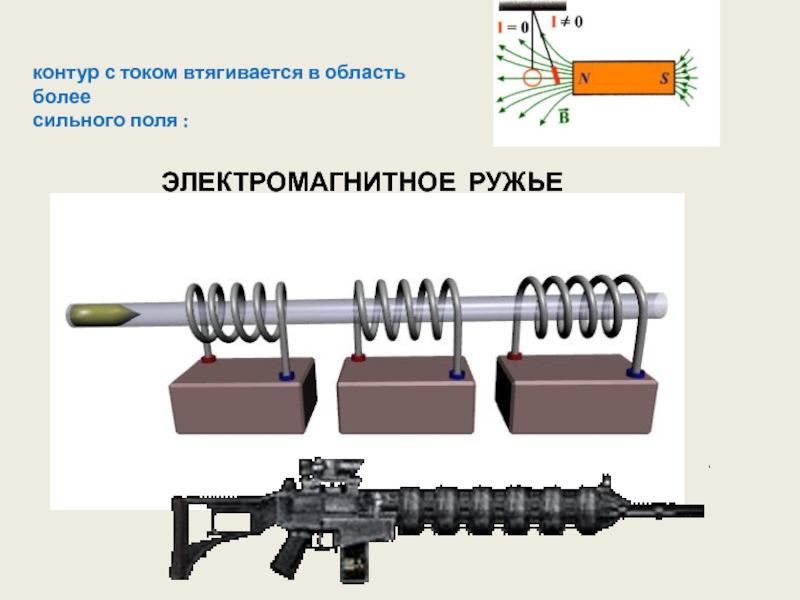
- 7. ЭЛЕКТРОМАГНИТНОЕ РУЖЬЕ контур с током втягивается в область более сильного поля :
- 8. Основные уравнения магнитостатического поля в вакууме 1.
- 9. 2. Теорема о циркуляции вектора индукции магнитного
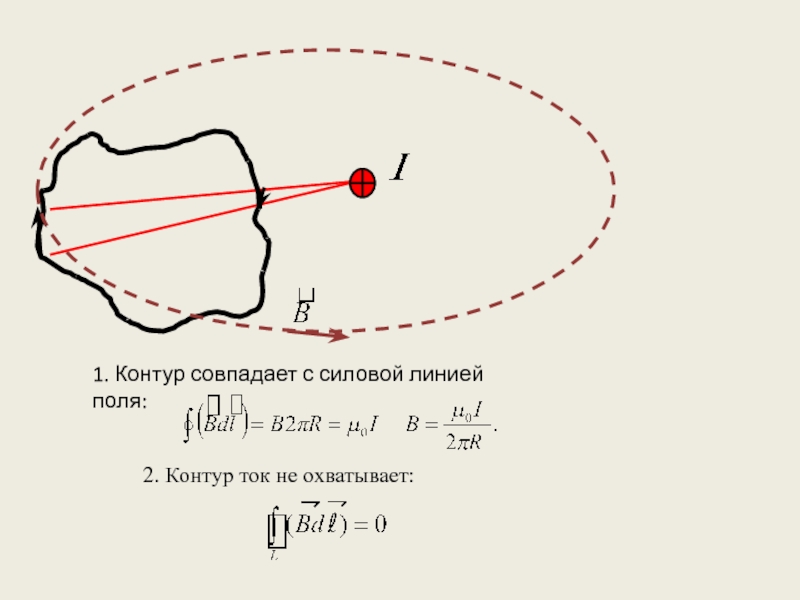
- 10. 2. Контур ток не охватывает: 1. Контур совпадает с силовой линией поля:
- 11. 3. Контур охватывает несколько токов: Каждый ток
- 12. Циркуляция вектора индукции магнитного поля в
- 13. Справка из векторной алгебры: векторное поле, в
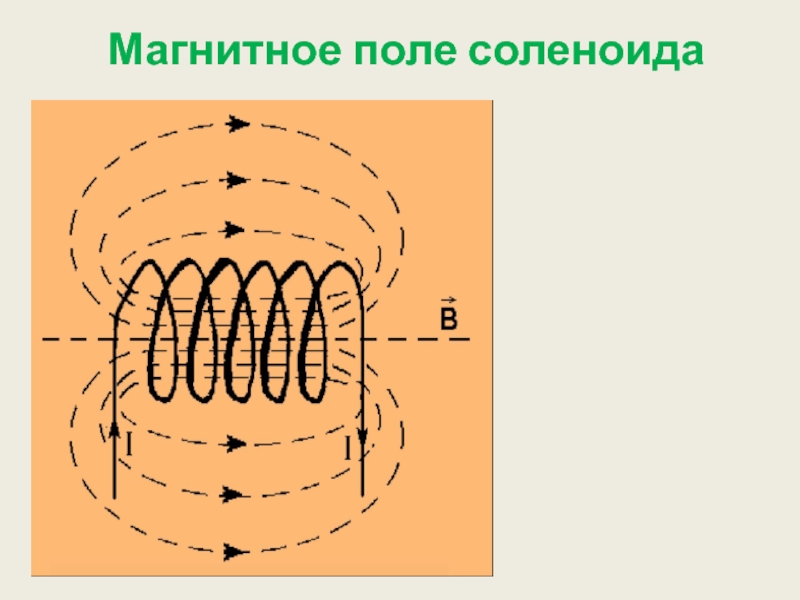
- 14. Магнитное поле соленоида
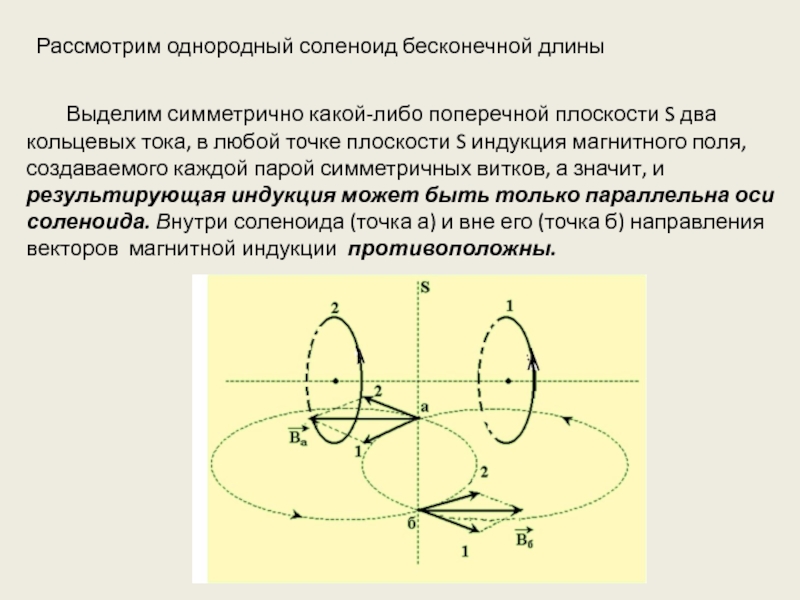
- 15. Выделим симметрично какой-либо поперечной плоскости S два
- 16. Величина индукции магнитного поля внутри бесконечно длинного
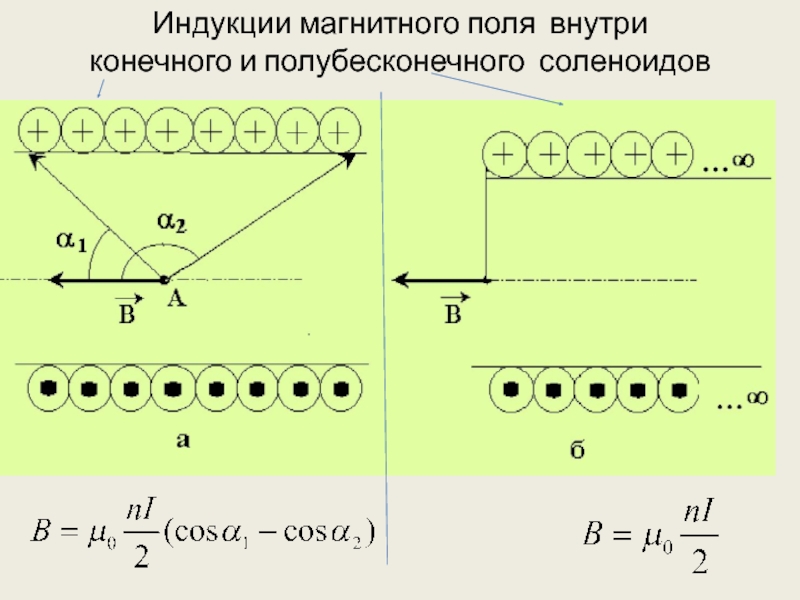
- 17. Индукции магнитного поля внутри конечного и полубесконечного соленоидов
- 18. Поле
- 19. Магнитное поле тороида
- 20. Для тонкого тороида индукция
- 21. Резюме по теме «Магнитостатическое поле в вакууме».
Слайд 2
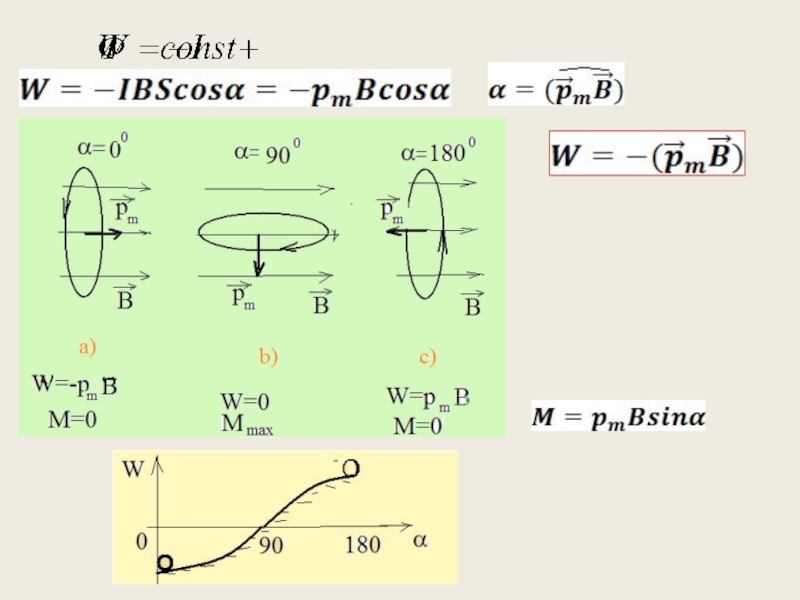
Потенциальная энергия контура с током
в магнитном поле
Работа по перемещению контура
Величина механической работы определяется убылью потенциальной энергии контура с током в постоянном магнитном поле.
Работа сил поля по перемещению контура с постоянным током в магнитостатическом поле:
Слайд 4Положение контура
соответствует минимуму его потенциальной энергии, т.е. состоянию устойчивого равновесия.
Слайд 5
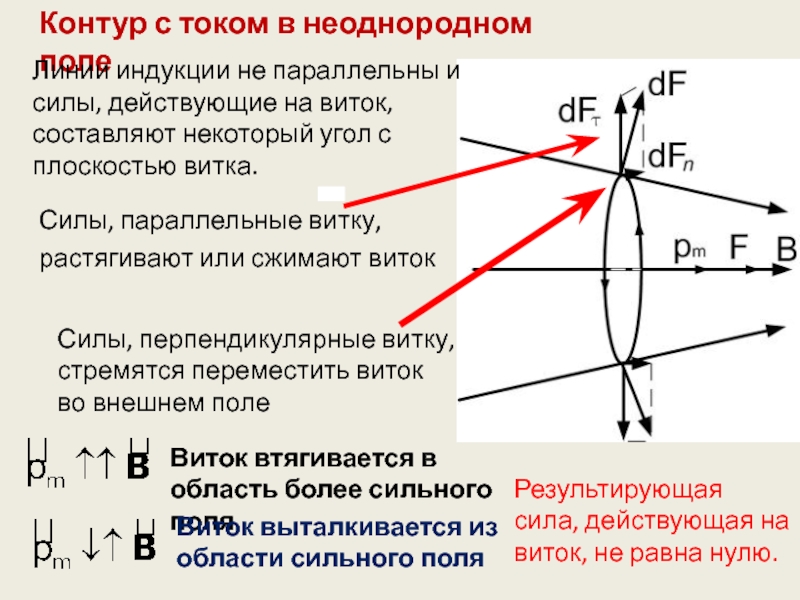
Контур с током в неоднородном поле
Линии индукции не параллельны и силы,
Силы, параллельные витку,
растягивают или сжимают виток
Силы, перпендикулярные витку, стремятся переместить виток во внешнем поле
Виток втягивается в область более сильного поля
Виток выталкивается из области сильного поля
Результирующая сила, действующая на виток, не равна нулю.
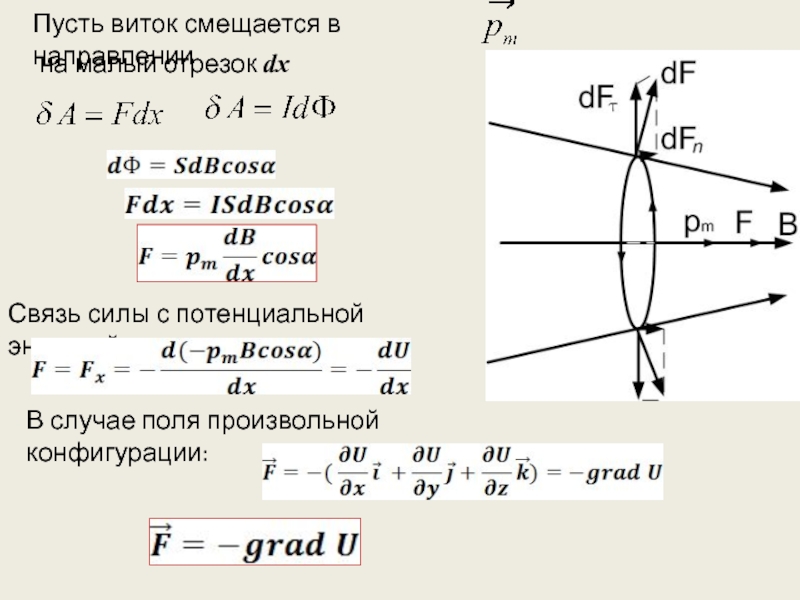
Слайд 6Пусть виток смещается в направлении
на малый отрезок dx
Связь силы с
В случае поля произвольной конфигурации:
Слайд 8Основные уравнения магнитостатического поля в вакууме
1. Теорема Гаусса для магнитного поля
Линии магнитной индукции всегда замкнуты, т.е. не имеют ни начала, ни конца.
Отсутствие в природе магнитных зарядов приводит к тому, что для произвольной замкнутой поверхности, расположенной в магнитном поле, поток вектора сквозь нее всегда равен нулю.
-интегральная форма записи теоремы Гаусса.
Слайд 92. Теорема о циркуляции вектора индукции магнитного поля.
Эксперимент:
Циркуляция вектора индукции
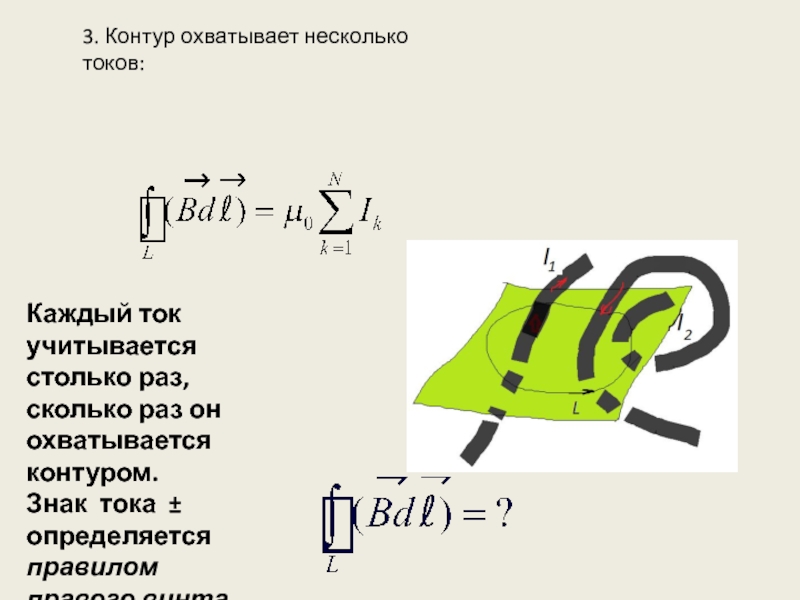
Слайд 113. Контур охватывает несколько токов:
Каждый ток учитывается столько раз, сколько раз
Знак тока ± определяется правилом правого винта.
Слайд 12Циркуляция вектора индукции магнитного поля в вакууме по произвольному замкнутому
-интегральная форма записи теоремы о циркуляции вектора .
Отсюда следует, что источниками стационарного магнитного поля являются постоянные токи проводимости.
Слайд 13Справка из векторной алгебры: векторное поле, в котором циркуляция вектора по
Стационарное магнитное поле является вихревым.
Слайд 15 Выделим симметрично какой-либо поперечной плоскости S два кольцевых тока, в любой
Рассмотрим однородный соленоид бесконечной длины
Слайд 16Величина индукции магнитного поля внутри бесконечно длинного соленоида:
Магнитное поле бесконечного
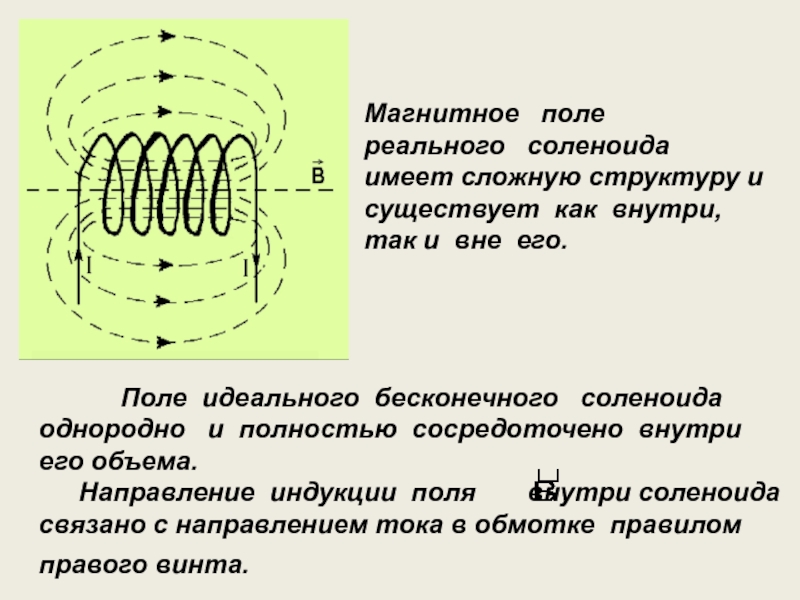
Слайд 18 Поле идеального бесконечного соленоида
Направление индукции поля внутри соленоида связано с направлением тока в обмотке правилом правого винта.
Магнитное поле реального соленоида имеет сложную структуру и существует как внутри, так и вне его.
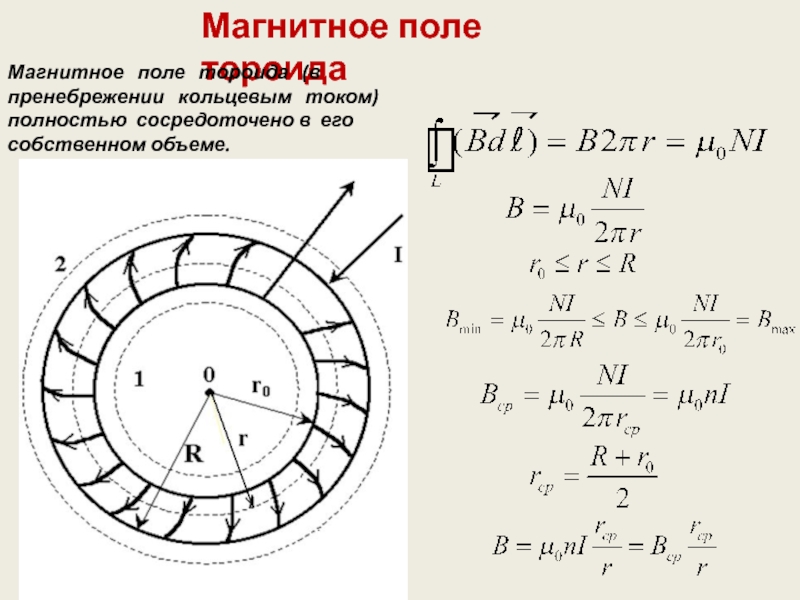
Слайд 19Магнитное поле тороида
Магнитное поле тороида (в пренебрежении
Слайд 20
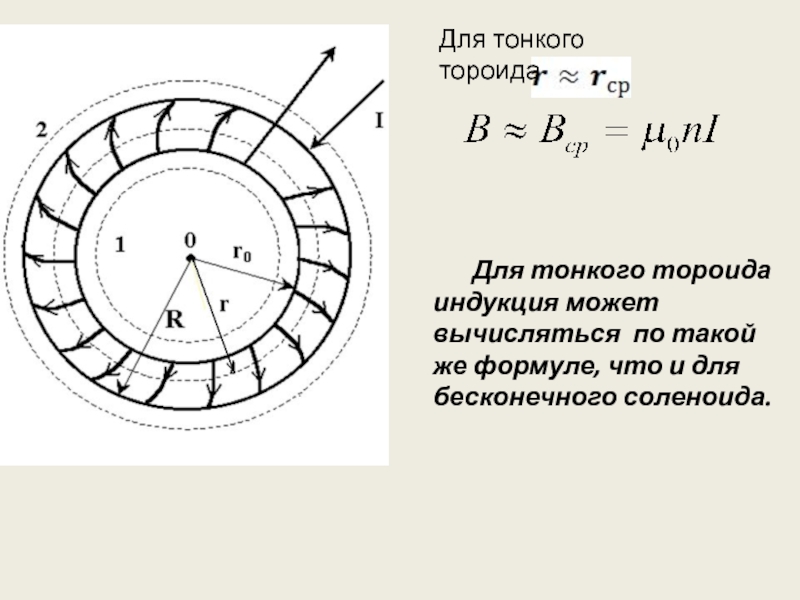
Для тонкого тороида индукция может вычисляться по такой же формуле,
Для тонкого тороида
Слайд 21Резюме по теме «Магнитостатическое поле в вакууме».
Любое магнитостатическое поле в
1. Теорема Гаусса для вектора :
Из нее следует, что линии магнитной индукции всегда замкнуты или уходят на бесконечность, т.е. в природе отсутствуют магнитные заряды, на которых обрывались бы эти линии .
2. Теорема о циркуляции вектора , которая является обобщением закона Био-Савара_Лапласа:
Из нее следует, что источниками стационарного магнитного поля являются постоянные токи проводимости.