- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейные цепи при несинусоидальных периодических токах презентация
Содержание
- 1. Линейные цепи при несинусоидальных периодических токах
- 2. Несинусоидальные токи Периодическими несинусоидальными токами и напряжениями
- 3. Разложение периодических функций. Характеристики несинусоидальных величин
- 4. Разложение периодических функций. Где
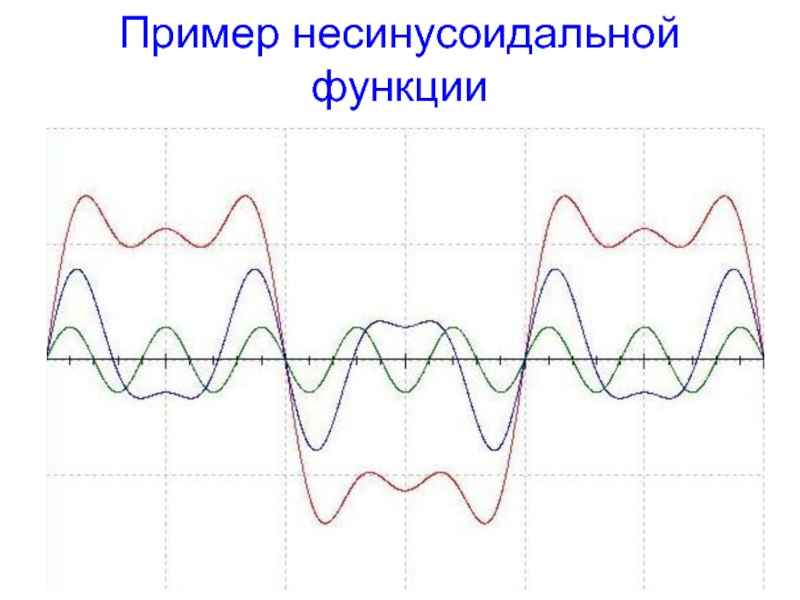
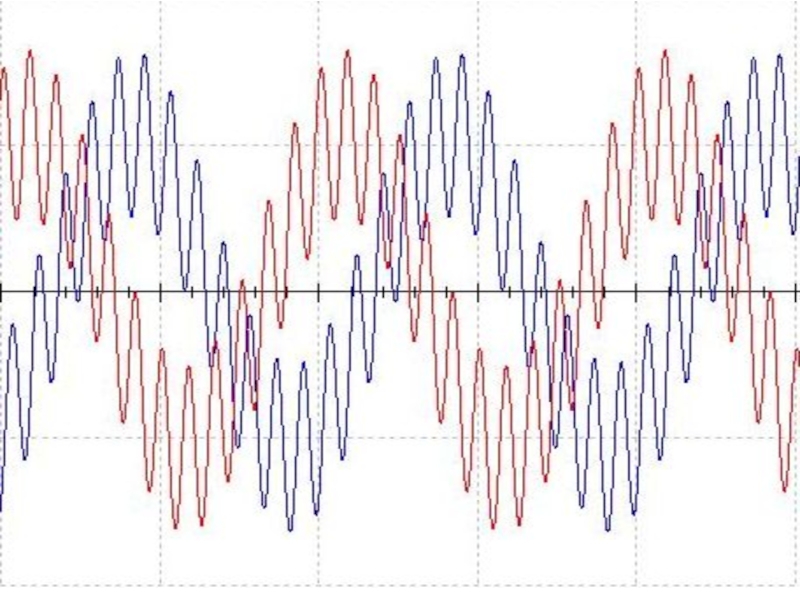
- 5. Пример несинусоидальной функции
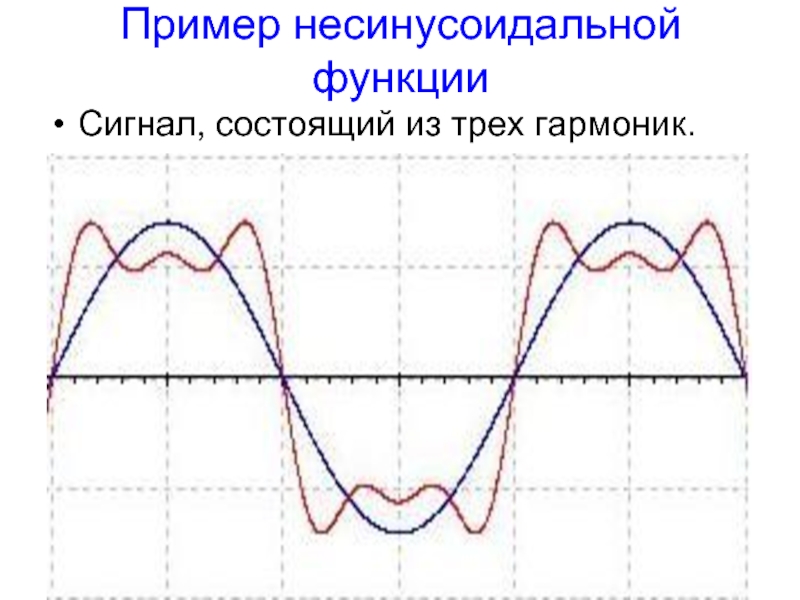
- 6. Пример несинусоидальной функции Сигнал, состоящий из трех гармоник.
- 7. типы периодических несинусоидальных функций 1. Кривые,
- 8. типы периодических несинусоидальных функций 2. Кривые, симметричные
- 9. типы периодических несинусоидальных функций 3. Кривые, симметричные
- 10. Величины, характеризующие несинусоидальные токи Максимальное значение –
- 11. Величины, характеризующие несинусоидальные токи Коэффициент амплитуды
- 12. Величины, характеризующие несинусоидальные токи Действующим значением периодической
- 13. Величины, характеризующие несинусоидальные токи На практике действующее
- 14. Мощность в цепях периодического несинусоидального тока
- 15. Мощность в цепях периодического несинусоидального тока Среднее
- 16. Мощность в цепях периодического несинусоидального тока Полная
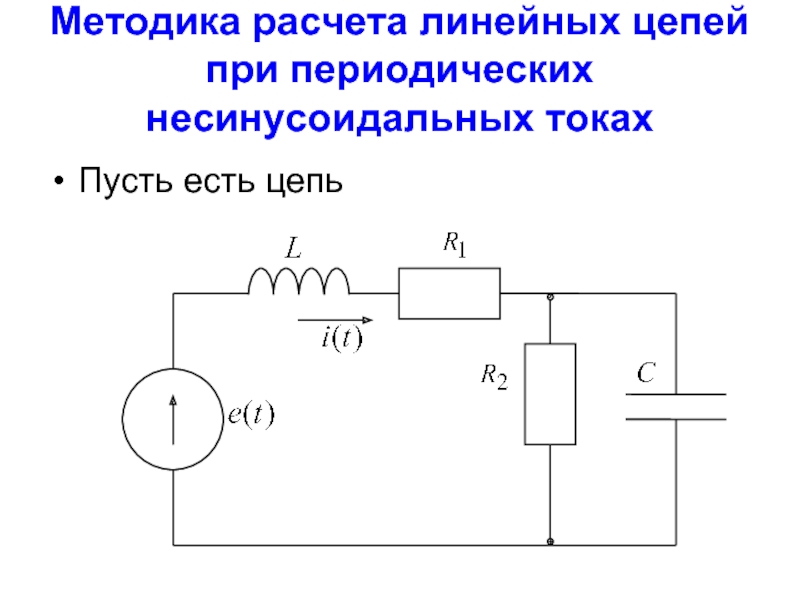
- 17. Методика расчета линейных цепей при периодических
- 18. Методика расчета линейных цепей при периодических
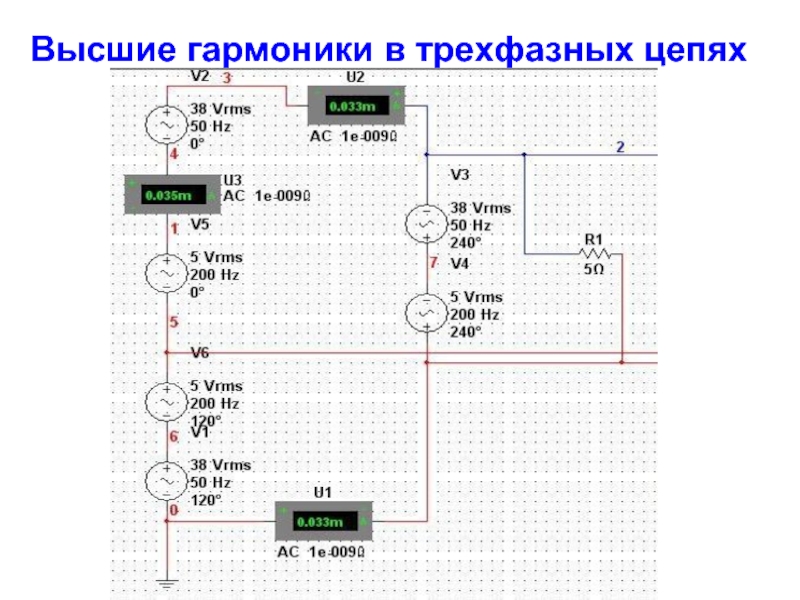
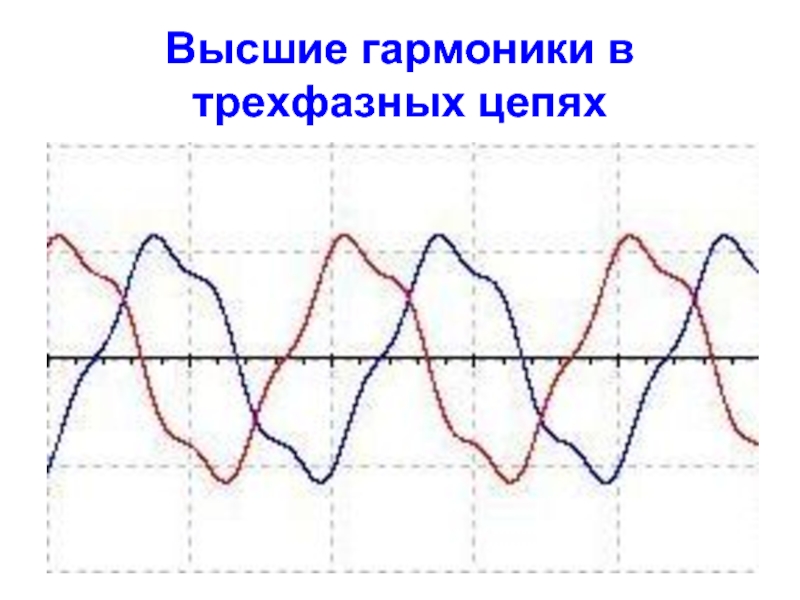
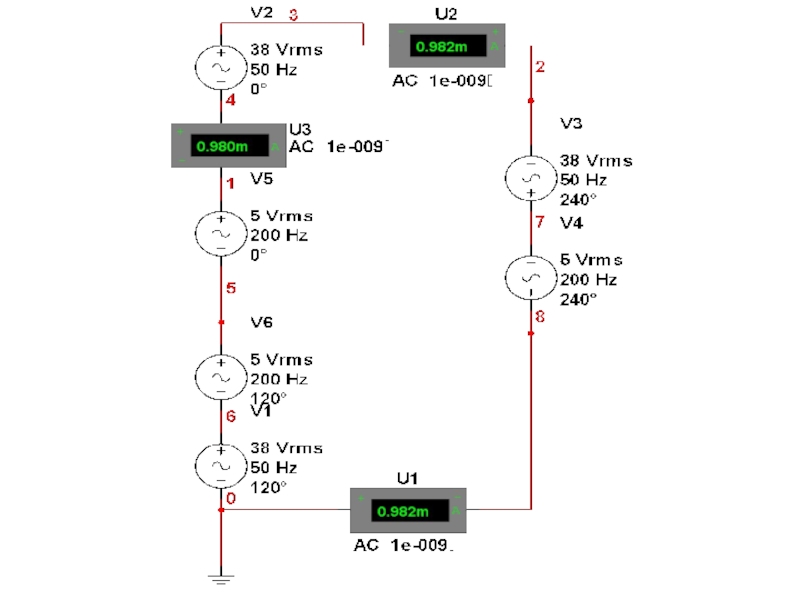
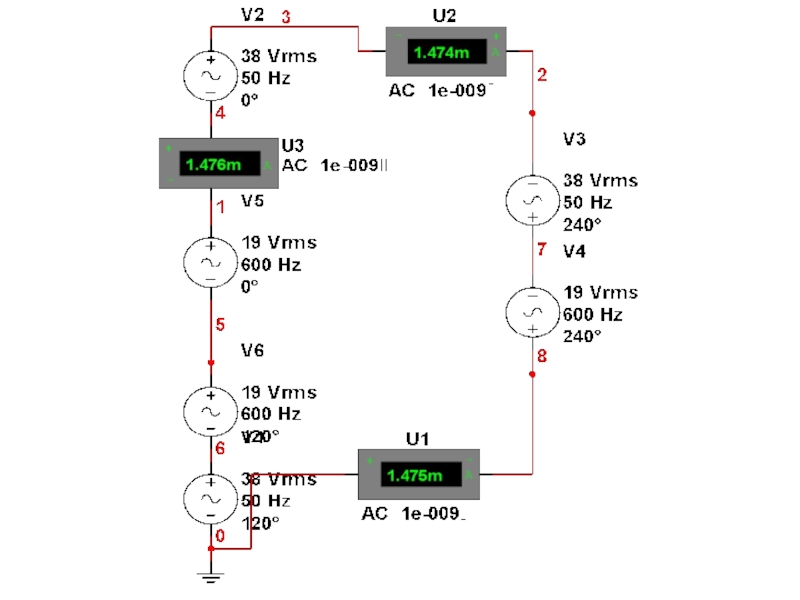
- 19. Высшие гармоники в трехфазных цепях Рассмотрим особенности
- 20. Высшие гармоники в трехфазных цепях Если фазы
- 21. Высшие гармоники в трехфазных цепях
- 22. Высшие гармоники в трехфазных цепях
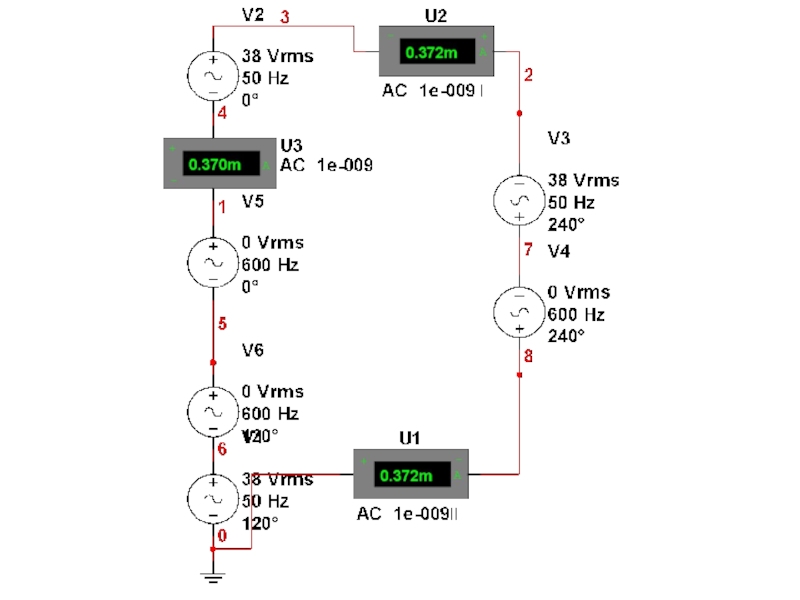
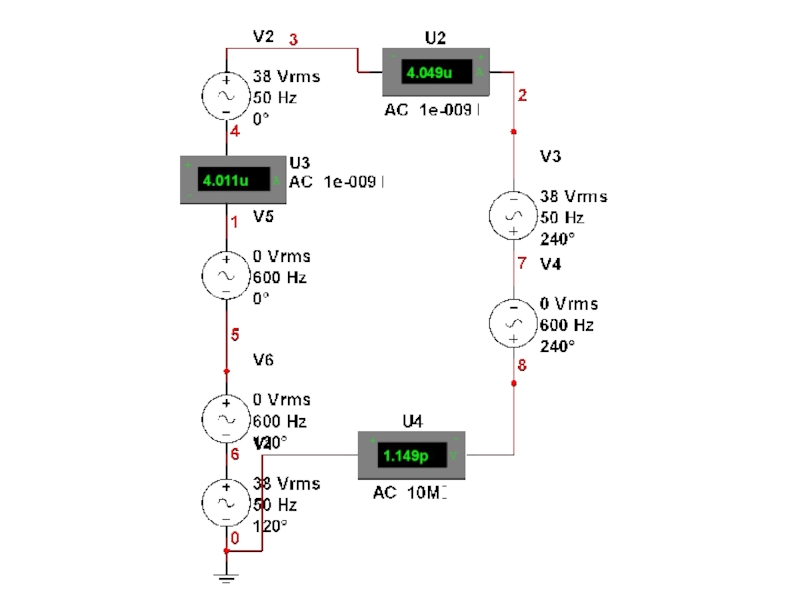
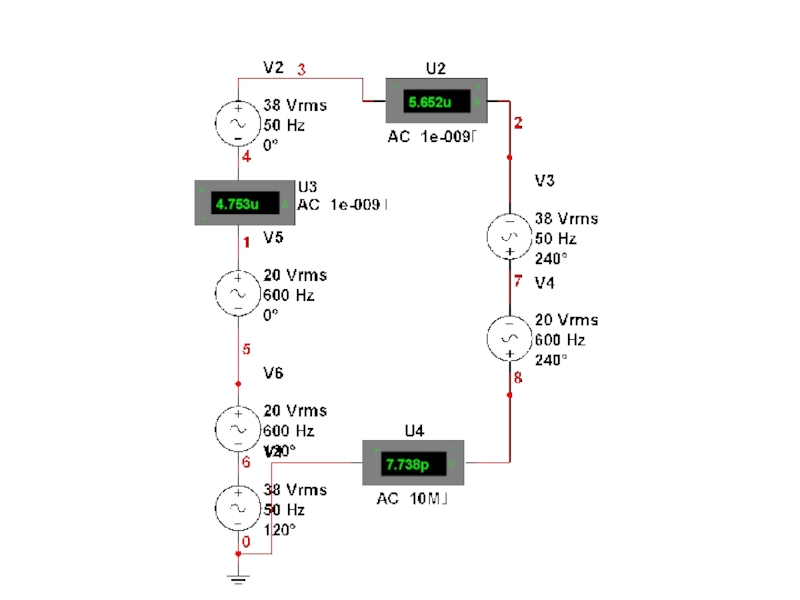
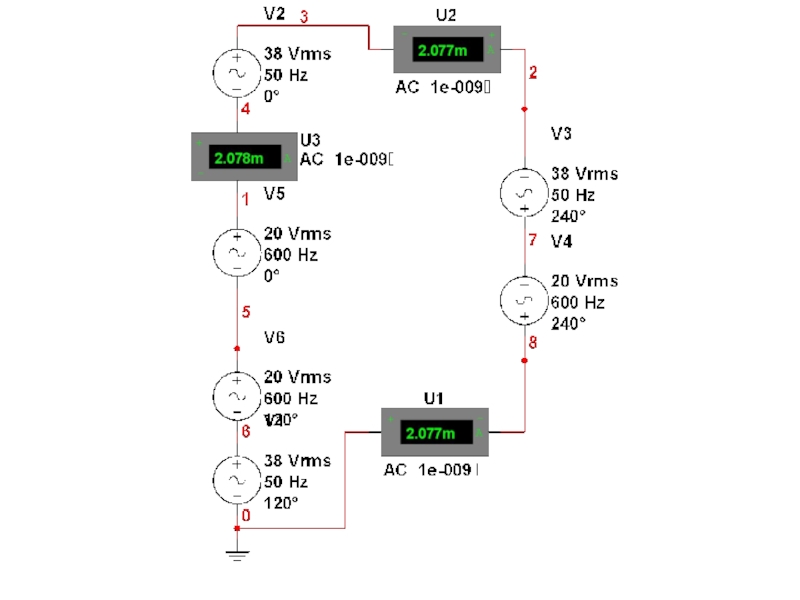
- 30. Пример расчёта По графу составить принципиальную схему
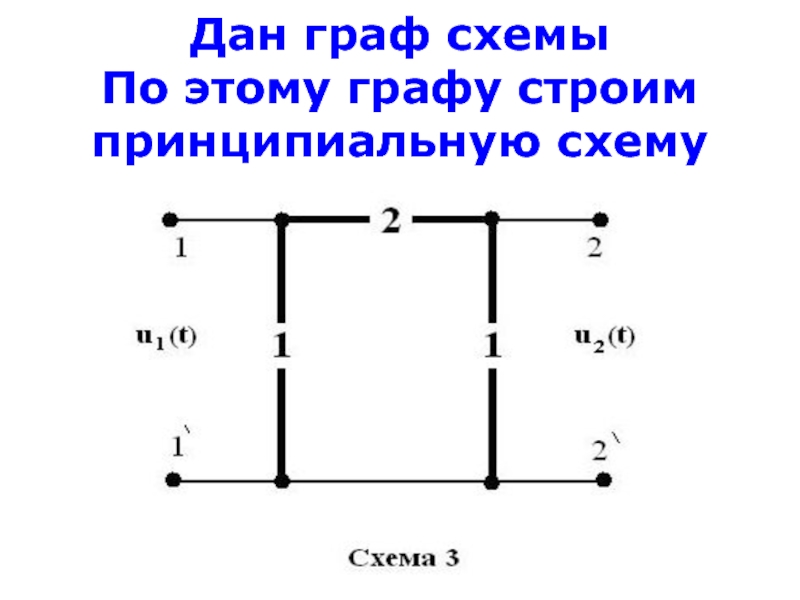
- 31. Дан граф схемы По этому графу строим принципиальную схему
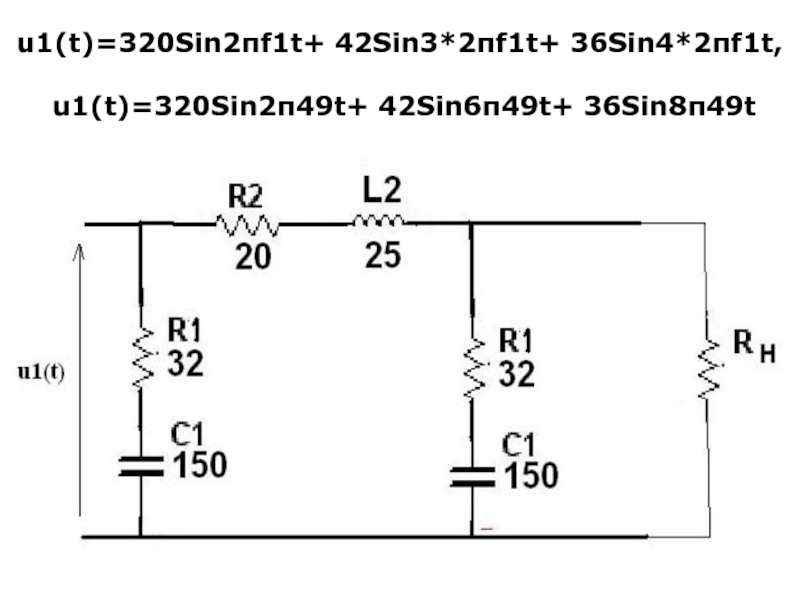
- 32. u1(t)=320Sin2πf1t+ 42Sin3*2πf1t+ 36Sin4*2πf1t, u1(t)=320Sin2π49t+ 42Sin6π49t+ 36Sin8π49t
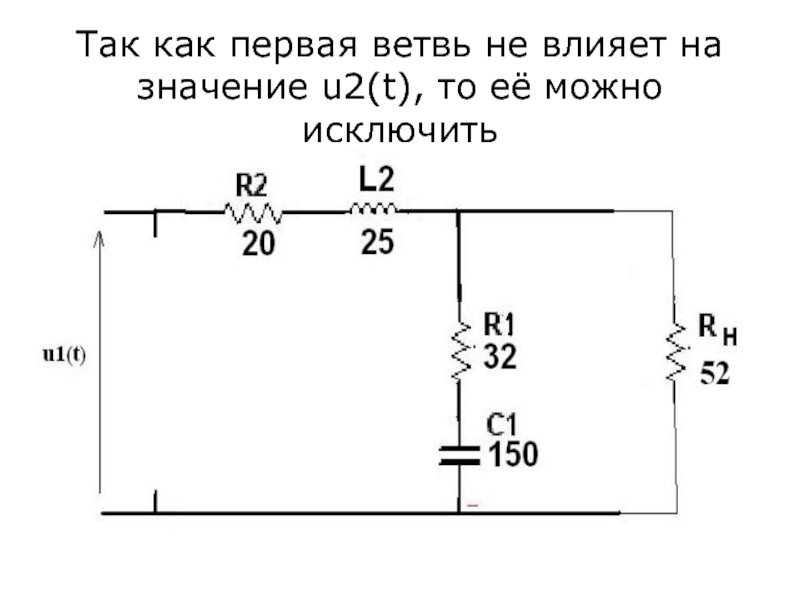
- 33. Так как первая ветвь не влияет на значение u2(t), то её можно исключить
- 34. Определяется комлекс напряжения для каждой гармоники Тогда
- 35. Переводится комплексное значение в форму мгновенного значения
- 36. Благодарю за внимание
Слайд 2Несинусоидальные токи
Периодическими несинусоидальными токами и напряжениями называются токи и напряжения, изменяющиеся
Слайд 3Разложение периодических функций.
Характеристики несинусоидальных величин
Для анализа процессов в линейных электрических
Слайд 4Разложение периодических функций.
Где
первая (основная) гармоника,
высшие гармоники,
Слайд 7типы периодических несинусоидальных функций
1. Кривые, симметричные относительно оси абсцисс. К
Слайд 8типы периодических несинусоидальных функций
2. Кривые, симметричные относительно
оси ординат,
Отсутствуют постоянная и косинусные
составляющие, т.е., .
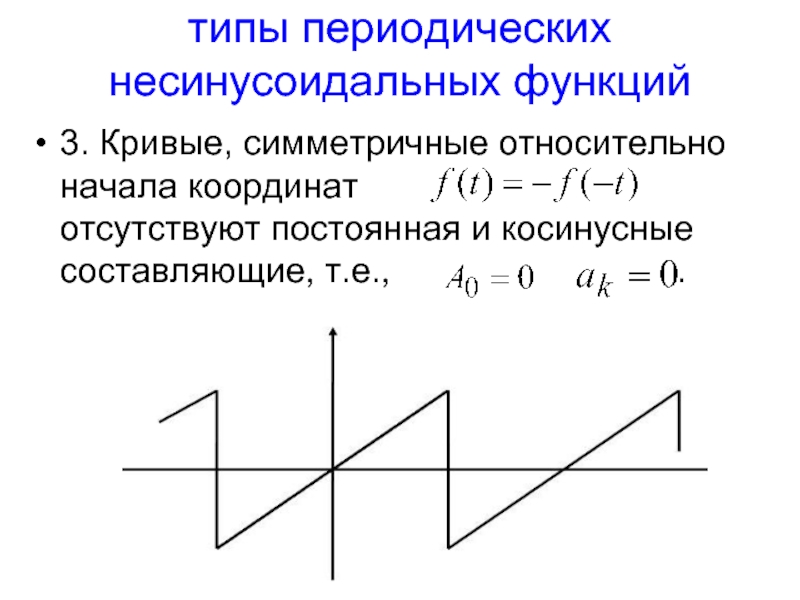
Слайд 9типы периодических несинусоидальных функций
3. Кривые, симметричные относительно начала координат
Слайд 10Величины, характеризующие несинусоидальные токи
Максимальное значение – I max
Действующее значение
Среднее
Среднее за период значение
(постоянная составляющая)
Слайд 11Величины, характеризующие несинусоидальные токи
Коэффициент амплитуды
Коэффициент формы
Коэффициент искажений
Коэффициент гармоник
Слайд 12Величины, характеризующие несинусоидальные токи
Действующим значением периодической несинусоидальной переменной называется среднеквадратичное за
Слайд 13Величины, характеризующие несинусоидальные токи
На практике действующее значение переменной определяется на основе
Слайд 14Мощность в цепях периодического несинусоидального тока
Допустим, ток и напряжение являются
Слайд 15Мощность в цепях периодического несинусоидального тока
Среднее за период значение произведения синусоидальных
Где
Реактивная мощность
Слайд 16Мощность в цепях периодического несинусоидального тока
Полная мощность
где Т – мощность
Слайд 18Методика расчета линейных цепей при периодических
несинусоидальных токах
Определить мгновенные значения токов
Для этого используется следующий алгоритм:
1. ЭДС и токи источников раскладываются в ряды Фурье.
2. ЭДС и токи источников раскладываются в ряды Фурье.
3. Искомые величины определяются как алгебраические суммы соответствующих гармонических.
Слайд 19Высшие гармоники в трехфазных цепях
Рассмотрим особенности работы трехфазных систем, обусловленные наличием
:
Слайд 20Высшие гармоники в трехфазных цепях
Если фазы генератора соединены в треугольник, то
Слайд 30Пример расчёта
По графу составить принципиальную схему
Вести расчёт для каждой гармоники отдельно
Алгебраически
Построить графики требуемых функций
Слайд 34Определяется комлекс напряжения для каждой гармоники
Тогда выходное напряжение определяется по формуле
где
Слайд 35Переводится комплексное значение в форму мгновенного значения и затем гармоники складываются
В комплексной форме гармоники складывать нельзя