- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 8. Аналитическая механика. Теорема Эмми Нётер презентация
Содержание
- 1. Лекция 8. Аналитическая механика. Теорема Эмми Нётер
- 2. 1. ЗАМЕНА ПЕРЕМЕННЫХ
- 3. 2. ПРЕОБРАЗОВАНИЕ ВАРИАЦИОННОЙ СИММЕТРИИ Преобразование вариационной симметрии
- 4. 3. ДРУГИЕ ПРЕОБРАЗОВАНИЯ СИММЕТРИИ Дивергентные симметрии: такие,
- 5. 4. ФОРМУЛИРОВКА ТЕОРЕМЫ ЭММИ НЁТЕР Тогда у
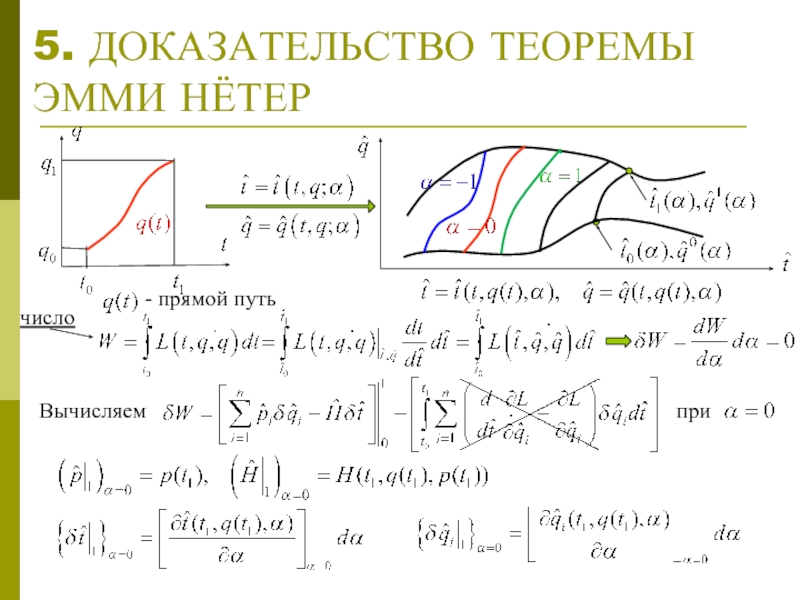
- 6. 5. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЭММИ НЁТЕР
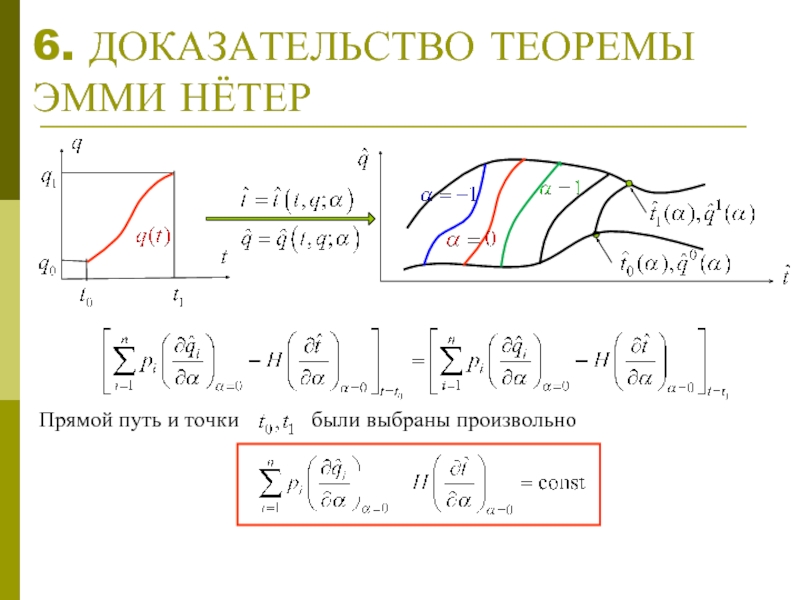
- 7. 6. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЭММИ НЁТЕР
- 8. 7. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Условие вариационной
- 9. 8. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА ДЛЯ ЦИКЛИЧЕСКИХ КООРДИНАТ
- 10. 9. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ Условие вариационной
- 11. 10. ЗАКОН СОХРАНЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА Условие вариационной
- 12. 11. ПРИМЕР В.Ф. ЖУРАВЛЕВА Условие вариационной
Слайд 32. ПРЕОБРАЗОВАНИЕ ВАРИАЦИОННОЙ СИММЕТРИИ
Преобразование вариационной симметрии в системе с функцией Лагранжа
Снята шляпа!
Снятие шляпы означает, что является решением той-же самой системы, что и
Преобразование симметрии в уравнениях Лагранжа –неособое преобразование расширенного координатного пространства, поточечно переводящее каждое решение в рещение той же системы.
Преобразование вариационной симметрии есть преобразование симметрии.
Есть симметрии отличные от вариационной
Слайд 43. ДРУГИЕ ПРЕОБРАЗОВАНИЯ СИММЕТРИИ
Дивергентные симметрии: такие, для которых выполняется условие
Добавление к
Следствие однородности системы уравнений Лагранжа
Конформные симметрии: такие, для которых выполняется условие
Слайд 54. ФОРМУЛИРОВКА ТЕОРЕМЫ ЭММИ НЁТЕР
Тогда у системы есть первый интеграл
Пусть материальная
тождественных при
Слайд 87. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Условие вариационной симметрии
Однопараметрическое семейство преобразований
Обобщенно консервативная
Закон сохранения энергии – следствие инвариантности лагранжиана системы относительно сдвига по времени
Слайд 98. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА ДЛЯ ЦИКЛИЧЕСКИХ КООРДИНАТ
Условие вариационной симметрии
Однопараметрическое семейство
Система с циклической координатой
Закон сохранения импульса для циклической координаты – следствие инвариантности лагранжиана системы относительно сдвига по этой координате
Слайд 109. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
Условие вариационной симметрии
Однопараметрическое семейство преобразований
Замкнутая система
Закон сохранения количества движения– следствие инвариантности лагранжиана системы относительно сдвига по пространственной координате
Слайд 1110. ЗАКОН СОХРАНЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА
Условие вариационной симметрии выполнено
Однопараметрическое семейство преобразований
Замкнутая
Закон сохранения кинетического момента– следствие инвариантности лагранжиана системы относительно поворотов.
Слайд 1211. ПРИМЕР В.Ф. ЖУРАВЛЕВА
Условие вариационной симметрии выполнено при
Семейство преобразований
Свободная