- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 42. Строение атома презентация
Содержание
- 1. Лекция 42. Строение атома
- 2. Атом водорода является простейшим атомом. Он состоит
- 3.
- 4.
- 5. Интересно оценить величину энергии по (41.16). Подставив
- 6.
- 7. Связь их с декартовыми показана на рисунке.
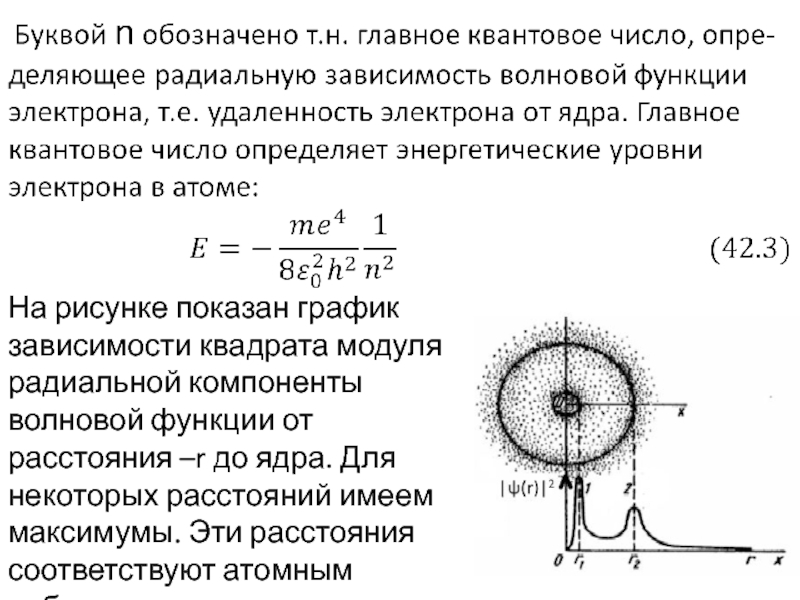
- 8. На рисунке показан график зависимости квадрата
- 9.
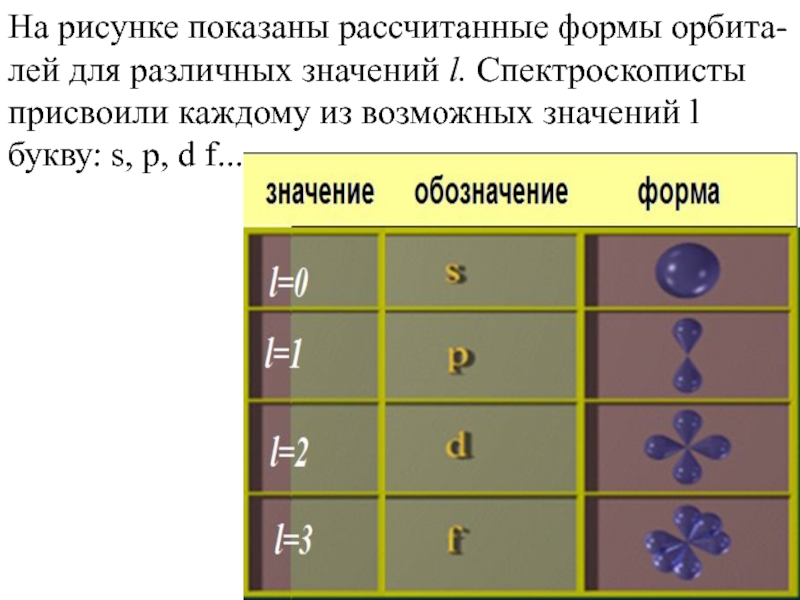
- 10. На рисунке показаны рассчитанные формы
- 12. Каждому значению главного квантового числа n соответствует
- 13. Для каждого значения l разрешено (2l +
- 14. Излучение и поглощение света атомами. Электрон,
- 15. Если фотон испускается в результате перехода между
- 16.
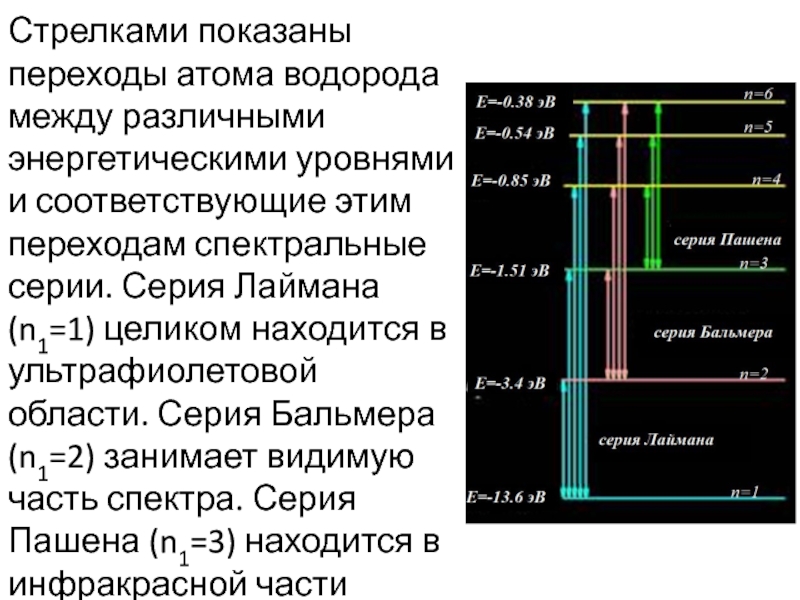
- 17. Стрелками показаны переходы атома водорода между различными
- 18.
- 19. Пятиминутка: Рассчитать длины волн в спектре излучения
- 20. Фундаментальные природные закономерности: законы сохранения энергии, импульса,
- 21. Аналогичный сюрприз можно ожидать от враща-тельного движения
- 22. Значение спинового числа (s) определяется свойствами симметрии
- 23. С учетом спинового числа состояние электрона в
- 24. При́нцип Па́ули (принцип запрета) - один из фундаментальных принципов
Слайд 2Атом водорода является простейшим атомом. Он состоит из протона и электрона,
Рассмотрим устройство атома с точки зрения квантовой механики. Локализация электрона в пределах атома озна-чает неопределенность его импульса, причем ΔpΔz≈h. В данной формуле неопределенности Δz – размер атома, скажем,- длина орбиты электрона. Положим Δz=2πr, где r- радиус атома. Тогда Δp=h/2πr, и p=± Δ p
Слайд 5Интересно оценить величину энергии по (41.16). Подставив значения величин, получим:
Е=-21.8*10-19
В микромире энергия измеряется в электрон-вольтах. 1эв=1.6*10-19 Дж. Поэтому Е=-13.6 эв.
Удивительно, что эти рассуждения на основе принципа неопределенности дают правильный результат величины энергии.
Уравнение движения электрона в атоме водорода
- Это уравнение Шредингера, записанное для трехмерного движения (три пространственные координаты) с потенциальной энергией поля точечного заряда ядра.
Слайд 7Связь их с декартовыми показана на рисунке. Кроме того вместо параметров
вращательного движения – момент инерции, мо-мент импульса. При этом результаты решения ока-зываются в принципе похожи на те, которые мы получали в случае одномерного движения ограни-ченной частицы. Энергия и момент импульса электрона оказываются квантованными, т.е. могут принимать только дискретный ряд значений, определяемых тремя целыми числами: n, l, m.
Слайд 8
На рисунке показан график зависимости квадрата модуля радиальной компоненты волновой функции
Слайд 10
На рисунке показаны рассчитанные формы орбита-лей для различных значений l. Спектроскописты
Слайд 11
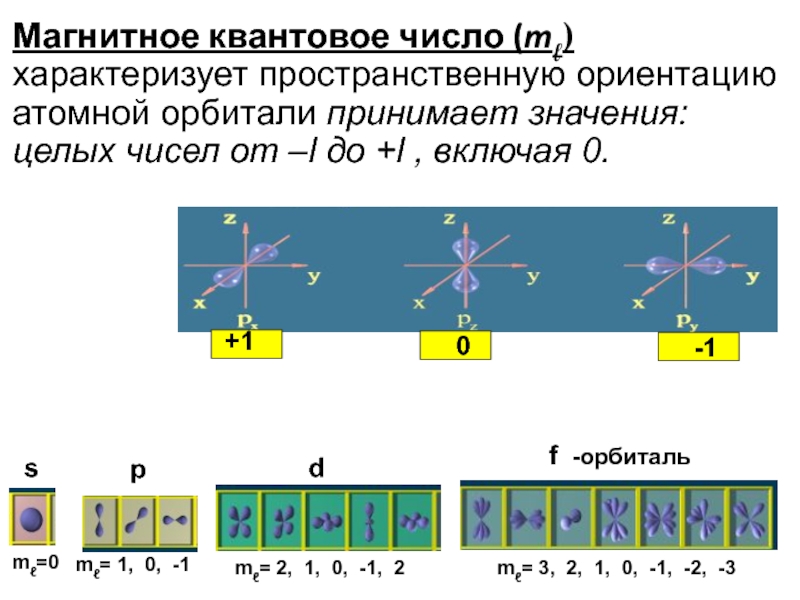
Магнитное квантовое число (mℓ) характеризует пространственную ориентацию атомной орбитали принимает значения: целых чисел от –l до +l , включая 0.
mℓ=0
mℓ= 1, 0, -1
mℓ= 2, 1, 0, -1, 2
mℓ= 3, 2, 1, 0, -1, -2, -3
s
p
d
f -орбиталь
+1
0
-1
Слайд 12Каждому значению главного квантового числа n соответствует энергетический уровень. Кроме то-го,
Слайд 13Для каждого значения l разрешено (2l + 1) значений m.
Например, l=4
-4, -3, -2, -1, 0, 1, 2, 3, 4
Получаем 9 возможных ориентаций орбитали f.
Все орбитали одного подуровня l при отсутствии внешнего магнитного поля обладают одинаковой энергией, но по разному ориентированы относительно друг друга
Слайд 14 Излучение и поглощение света атомами. Электрон, находящийся на энергетическом уровне
Слайд 15Если фотон испускается в результате перехода между уровнями с энергиями Еn1>
hν= Еn1- Еn2 (42.6)
Это соотношение определяет частоту колебаний или длину волны фотона.
Исследуя спектры излучения атомов, т.е. измеряя длины волн испускаемого света удается опреде-лить энергии их энергетических уровней.
Слайд 17Стрелками показаны переходы атома водорода между различными энергетическими уровнями и соответствующие
Слайд 19Пятиминутка: Рассчитать длины волн в спектре излучения атома водорода, соответствующих переходам
Слайд 20Фундаментальные природные закономерности: законы сохранения энергии, импульса, момента импульса являются выражением
Ограничение субнаночастицы в пространстве, как мы видели, приводит к сюрпризу: квантовонности ее импульса (импульс изменяется только скачками и не может быть нулевым).
Слайд 21Аналогичный сюрприз можно ожидать от враща-тельного движения частицы. Ее момент импульса
L=ħs,
где коэффициент s –спиновое число частицы.
Проявление спина электрона было обнаружено в опыте экспериментально.
Слайд 22Значение спинового числа (s) определяется свойствами симметрии частицы. Если она абсолютно
Если для самосовмещения частицы ее достаточно повернуть на 180о (например, заточенный с двух сторон карандаш), то спиновое число равно 2. Если для самосовмещения требуется поворот на 360о (заточенный с одной стороны карандаш), то s=1. Такие частицы названы бозонами. Фотон–бозон.
Можно представить ситуацию в которой для самосовмещение необходим поворот на 720о. В этом случае s=1/2. Такие частицы называют фермионами. Электрон - фермион.
Слайд 23С учетом спинового числа состояние электрона в атоме характеризуется 4 квантовыми
n – натуральное число: 1, 2, 3…;
l=0, 1, ..n-1;
m=±l, ±(l-1), …0. Возможное состояние электрона называется орбиталью (по аналогии с орбитой планеты, можно условно считать, что строение атома аналогично строению планетной системы).
Для понимания строений атомов определяющее значение имеет т.н. принцип Паули.
Слайд 24При́нцип Па́ули (принцип запрета) - один из фундаментальных принципов законов природы. Два и
Если речь идет об атоме, то в нем не могут быть два или более электрона с одинаковой четверкой квантовых чисел. Поскольку электроны занимают орбитали с наименьшими энергиями, можно определить электронное строение любого атома в невозбужденном состоянии.