- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 41. Рентгеновская трубка. Эффект Комптона. Введение в квантовую механику презентация
Содержание
- 1. Лекция 41. Рентгеновская трубка. Эффект Комптона. Введение в квантовую механику
- 2. Тормозное рентгеновское излучение Квантовая природа излучения
- 3. Но она не может объяснить наличие
- 4. Эффект Комптона. В этом опыте фотоны ведут
- 5. Опыт показал, что в рассеянном луче наряду
- 6. Упругое столкновение двух частиц – налетающего фотона,
- 7.
- 8.
- 9.
- 10. Это заявление было неожиданным. Но вскоре опыты
- 11. И электроны проявляют волновые свойства, например, в опыте Дж. Томсона (1928 г.)
- 12. Мы получаем критерий разграничения между микро и
- 13. Элементы квантовой механики. Начальный этап развития опирался
- 14. Ответ на этот вопрос также вытекает из
- 15. Для свободной частицы амплитуда Am не зависит
- 16.
- 17.
- 18. Принцип неопределенности. На первый взгляд этот принцип
- 19. Можно получить соотношение неопределенности для частицы, движущейся
- 20. Эта неопределённость означает наличие у прошедших электронов
- 21. Уравнение Шредингера Уравнение Шредингера играет в квантовой
- 22.
- 23.
- 24. Решение уравнения Шредингера определяется не только видом
- 25. Движение частиц в прямоугольной потенциальной яме Одна
- 26.
- 27.
- 28.
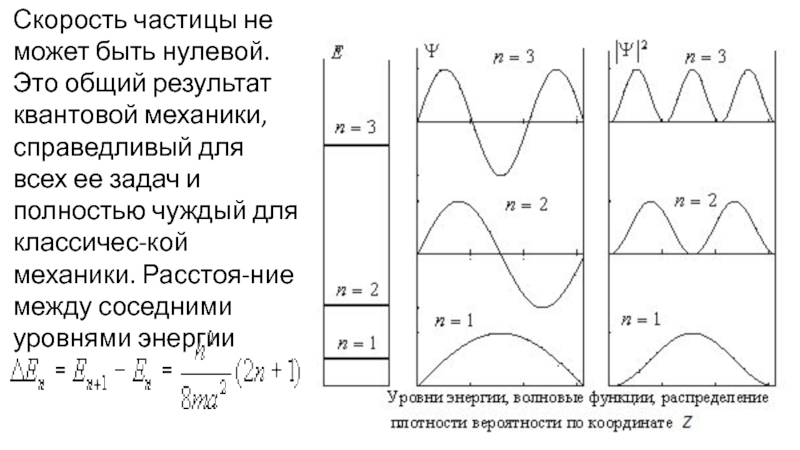
- 29. Скорость частицы не может быть нулевой. Это
- 30.
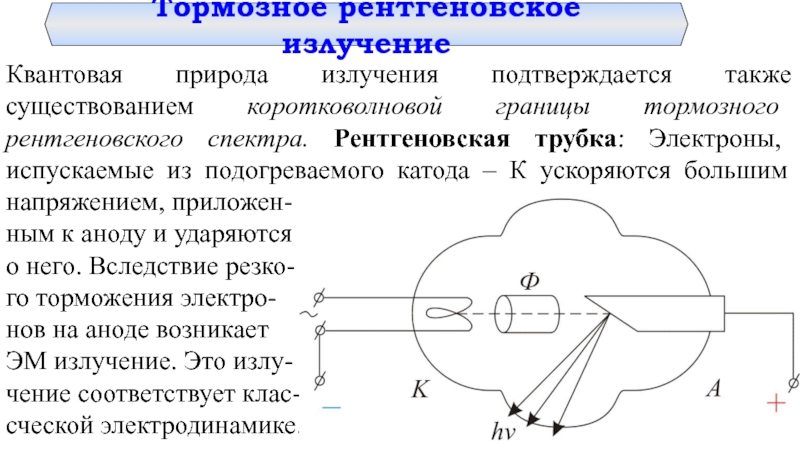
Слайд 2Тормозное рентгеновское излучение
Квантовая природа излучения подтверждается также существованием коротковолновой границы
ным к аноду и ударяются
о него. Вследствие резко-
го торможения электро-
нов на аноде возникает
ЭМ излучение. Это излу-
чение соответствует клас-
сческой электродинамике.
Слайд 3Но она не может объяснить наличие
коротковолновой границы тормозного
излучения -λmin.
раничение напрямую вытекает из кван-
товой природы излучения. если излу-
чение возникает за счёт энергии, теря-
емой электроном при торможении, то
энергия кванта hω не может превы-
сить энергию электрона: hν ≤ eU, отсюда λ≥Ch/(eU). (С- скорость света).
Т.о. Квантовые свойства света при излучении и поглощении не вызывали сомнений. Однако, в каком же виде существует и распространяется свет?.
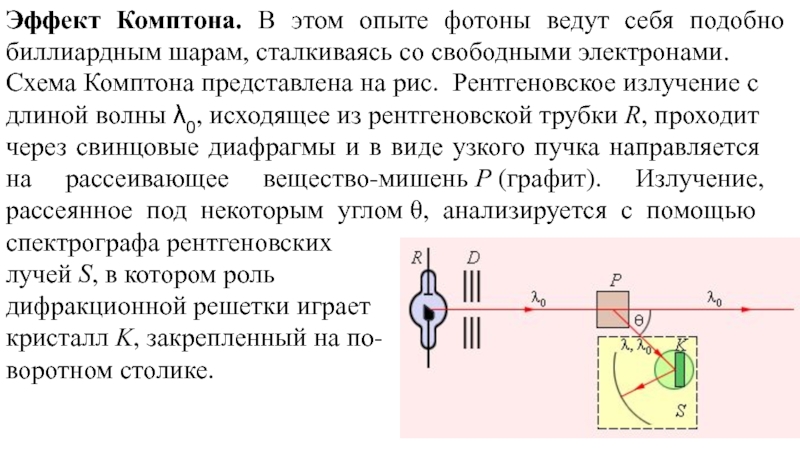
Слайд 4Эффект Комптона. В этом опыте фотоны ведут себя подобно биллиардным шарам,
Схема Комптона представлена на рис. Рентгеновское излучение с длиной волны λ0, исходящее из рентгеновской трубки R, проходит через свинцовые диафрагмы и в виде узкого пучка направляется на рассеивающее вещество-мишень P (графит). Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских
лучей S, в котором роль
дифракционной решетки играет
кристалл K, закрепленный на по-
воротном столике.
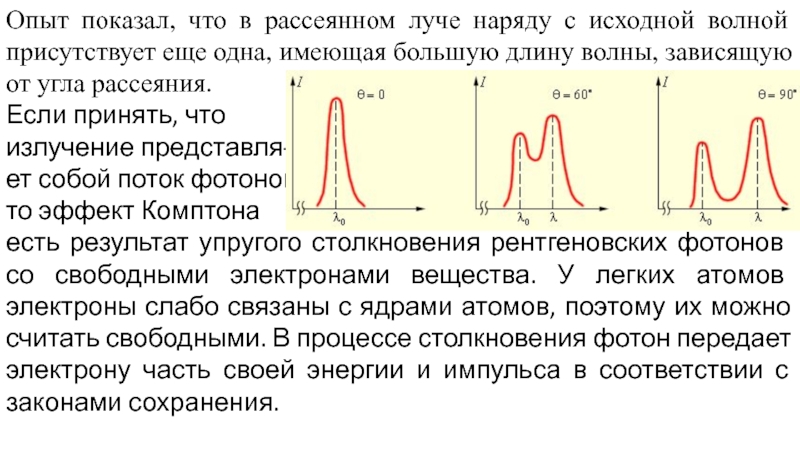
Слайд 5Опыт показал, что в рассеянном луче наряду с исходной волной присутствует
Если принять, что
излучение представля-
ет собой поток фотонов,
то эффект Комптона
есть результат упругого столкновения рентгеновских фотонов со свободными электронами вещества. У легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными. В процессе столкновения фотон передает электрону часть своей энергии и импульса в соответствии с законами сохранения.
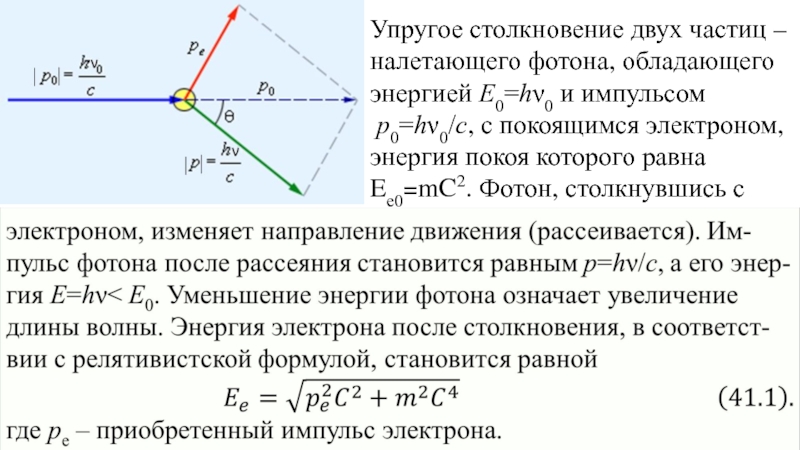
Слайд 6Упругое столкновение двух частиц – налетающего фотона, обладающего энергией E0=hν0 и импульсом
p0=hν0/c, с покоящимся электроном, энергия покоя которого равна Eе0=mC2. Фотон, столкнувшись с
Слайд 10Это заявление было неожиданным. Но вскоре опыты Дэвиссона обнаружили волновые свойства
λ=6.6*10-34Дж*с/(10-4Кг*10м/с)=6.6*10-29м. Это невообразимо малая длина, на много порядков меньшая размеров атомов. Следовательно для обычных макро частиц длина сопутствующей волны, практичес-ки, нулевая, и обнаружить волновые эффекты невозможно. Другое дело – микрочастицы. Например для электрона со скоростью 100 м/с λ=6.6*10-34Дж*с/(9.1-31Кг*100м/с)=6*10-6м .
Слайд 12Мы получаем критерий разграничения между микро и макро частицами: к микрочастицами
Новая механика для микрочастиц получила два названия: иногда ее называют волновой, а иногда – квантовой механикой. Отличие ее от классической состоит в том, что она определяет не координаты движущейся частицы, а сопутствующую движению волну. Математическое выражение этой волны назвали волновой функцией и обозначается буквой ψ (пси).
Слайд 13Элементы квантовой механики.
Начальный этап развития опирался на известные законы оптики, которые
По аналогии, для любой свободно движущийся частицы с энергией E=mv2/2 и импульсом p=mv можем написать уравнение сопутствующей волны a=Amcos(ωt-kz), где ω=Е/ħ, k=p/ħ. Но если для света величина E– это световой вектор, то какой смысл величины «а» в уравнении волны свободной частицы?
Слайд 14Ответ на этот вопрос также вытекает из аналогии с оптикой. Там
Интенсивность света определяется количеством фотонов, попада-ющих в данную область пространства в единицу времени. Следовательно, квадрат амплитуды волновой функции (Am)2 будет пропорционален количеству частиц, попадающих в данную область в единицу времени. Если же речь идет об одной движущейся частице, то (Am)2 представляет собой вероятность попадания частицы в данную область пространства. Таков физический смысл волновой функции.
Слайд 15Для свободной частицы амплитуда Am не зависит от координаты, следовательно, вероятность
Ограничим свободу частицы двумя стенками, перпендикулярными оси Z. Расстояние между стенками – l и они упруго отражают частицу. Классическая частица может иметь любую скорость. Она ударяется о стенку, отскакивает без потери скорости, ударяется о другую стенку и т.д.
С точки зрения квантовой механики ситуа-
ция иная. Движению частице вправо соот-
Ветствует волновая функция ψ1=Amcos(ωt-kz)
А движению влево – ψ2=Amcos(ωt+kz). Об-
щая волновая функция равна сумме ψ=ψ1+ψ2
Слайд 18Принцип неопределенности. На первый взгляд этот принцип ка-жется довольно странным, однако
Слайд 19Можно получить соотношение неопределенности для частицы, движущейся между двумя стенками. Ее
Пусть поток электронов проходит через узкую щель. Казалось бы это поток, пройдя щель, засветит на экране узкую
полоску, с шириной, равной ширине щели Δх.
Однако, вследствие принципа неопределенности
после прохождения щели импульс электронов в
направлении оси Х станет неопределенным: ΔхΔрх=h.
Слайд 20Эта неопределённость означает наличие у прошедших электронов скорости в направлении оси
А отношение f/L=α – угол, на который рассеется электронный поток после щели: α= λ/ Δx. Эта формула для ширины главного дифракци-онного максимума при дифракции на щели. Т.о. соотношение неопределенностей позволяет в упрощенной форме определить некоторые параметры дифракции микрочастиц.
А что можно сказать об обычных макрочастицах, действует ли для них соотношение неопределенностей. Конечно действует. Однако, огромная их масса и размеры пространства делает неопределен-ность импульса и скорости столь малыми, что обнаружить их невозможно.
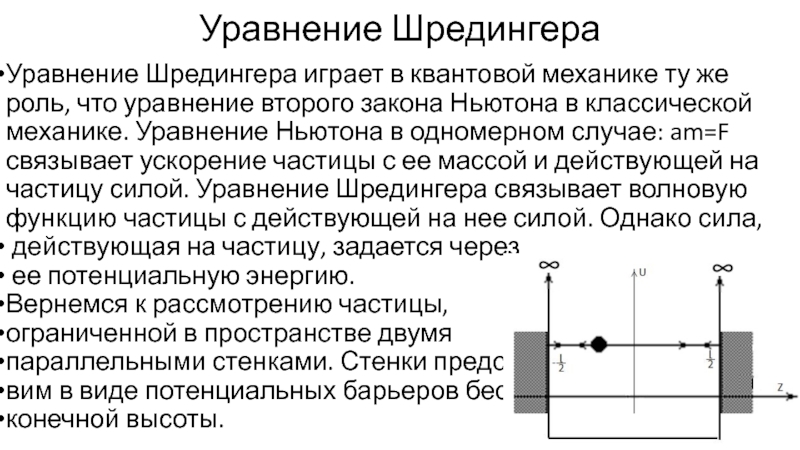
Слайд 21Уравнение Шредингера
Уравнение Шредингера играет в квантовой механике ту же роль, что
действующая на частицу, задается через
ее потенциальную энергию.
Вернемся к рассмотрению частицы,
ограниченной в пространстве двумя
параллельными стенками. Стенки предста-
вим в виде потенциальных барьеров бес-
конечной высоты.
Слайд 24Решение уравнения Шредингера определяется не только видом потенциальной функции U(z), но
Если частица находится в потенциальной яме, то вероятность найти ее вне ямы обращается в нуль; следовательно, здесь
граничное условие состоит в том, что вероятность найти частицу при значениях, больших | l/2 | обращается в нуль. Этому граничному условию удовлетворяют лишь определенные значения Е (будем обозначать их Еn) и соответствующие ψn. Значения Еn называются собственными значениями, а cответствующие волновые функции —ψn собственными функциями.
Рассмотрим простейшие примеры решения уравнения Шредингера.
Слайд 25Движение частиц в прямоугольной потенциальной яме
Одна из простейших задач о движении
Изменение потенциальной энергии по оси z описывается формулой:
U=0 при 0
В мире микрочастиц взаимодействие протона и нейтрона в ядре приближенно описывается прямоугольным потенциалом. Этот же потенциал очень грубое приближение к задаче о движении электрона в атоме.