- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1. Экспериментальные методы физики твердого тела презентация
Содержание
- 1. Лекция 1. Экспериментальные методы физики твердого тела
- 2. Лекция 1 Слайд 2 КРИСТАЛЛОГРАФИЯ Сиротин Ю.И., Шаскольская
- 3. Лекция 1 Слайд 3 Темы лекции: Кристаллические и
- 4. Лекция 1 Слайд 4 Вещество может находиться в
- 5. Лекция 1 Слайд 5 Одним из возможных принципов
- 6. Лекция 1 Слайд 6 Определение кристалла в кристаллографии:
- 7. Лекция 1 Слайд 7 Из этого определения →
- 8. Лекция 1 Слайд 8 Некоторые замечания относительно данного
- 9. Лекция 1 Слайд 9 Вблизи любой точки аморфного
- 10. Лекция 1 Слайд
- 11. Лекция 1 Слайд
- 12. Лекция 1 Слайд
- 13. Лекция 1 Слайд
- 14. Лекция 1 Слайд
- 15. Лекция 1 Слайд
- 16. Лекция 1 Слайд
- 17. Лекция 1 Слайд
- 18. Лекция 1 Слайд
- 19. Лекция 1 Слайд
- 20. Лекция 1 Слайд
- 21. Лекция 1 Слайд
- 22. Лекция 1 Слайд
- 23. Лекция 1 Слайд
- 24. Лекция 1 Слайд
- 25. Лекция 1 Слайд
- 26. Лекция 1 Слайд
Слайд 1Лекция 1 Слайд 1
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
ФИЗИКИ ТВЕРДОГО ТЕЛА
7 семестр 8 семестр
лекции
практические занятия практические занятия
2 час/неделю 2 час/неделю
зачет экзамен
Жабрев Геннадий Игоревич – доцент кафедры № 77
Слайд 2Лекция 1 Слайд 2
КРИСТАЛЛОГРАФИЯ
Сиротин Ю.И., Шаскольская М.П. Основы кристалло-физики. М.: Наука, 1979
Чупрунов Е.В., Хохлов А.Ф., Фаддеев М.А. Кристаллогра-фия. Учебник для вузов. М.: Издательство Физико-математической литературы, 2000.
Новиков И.И., Розин К.М. Кристаллография и дефекты кристаллической решетки. Учебник для вузов. М.: Металлургия, 1990.
Конвей Дж., Слоэн Н. Упаковки шаров, решетки и группы: В 2-х т. Пер. с англ. М.: Мир, 1990.
Современная кристаллография. т.1-3. М.: Наука, 1979.
Слайд 3Лекция 1 Слайд 3
Темы лекции:
Кристаллические и аморфные твердые тела.
Определение кристалла.
Элементарная ячейка.
Ближний
Монокристаллы и поликристаллы.
Слайд 4Лекция 1 Слайд 4
Вещество может находиться в одном из четырех агрегатных состояниях:
твердое,
жидкое,
газообразное,
плазменное.
Отличительные
стабильность формы,
характер тепловых движений атомов - малые колебания около положений равновесия.
Слайд 5Лекция 1 Слайд 5
Одним из возможных принципов классификации твердых тел является разделение
В физике: кристаллическое твердое тело – это то, у которого микроскопические физические характеристики являются периодической функцией пространственных координат (например, электронная плотность).
Т.к. твердые тела состоят из атомов, то для наличия подобной периодичности необходимо, чтобы и расположение атомов в кристаллическом твердом теле также являлось трехмерной периодической функцией координат. Кроме то-го, внешняя форма кристалла всегда представляет собой один из 48 правильных многогранников.
Слайд 6Лекция 1 Слайд 6
Определение кристалла в кристаллографии:
Кристаллическим твердым телом (кристаллом) называется
Слайд 7Лекция 1 Слайд 7
Из этого определения → любой кристалл можно предста-вить в
С помощью элементарных ячеек можно заполнить без про-пусков и наложений друг на друга весь объем кристалла.
В кристаллографии периодически повторяющаяся конфи-гурация называется мотивом.
Слайд 8Лекция 1 Слайд 8
Некоторые замечания относительно данного определения.
В твердом теле атомы, как
В твердом теле атомы всегда испытывают тепловые колебания отно-сительно положений равновесия. Данным обстоятельством в крис-таллографии пренебрегают и считают атомы неподвижными, а коор-динаты центров тяжести атомов совпадающими с положениями рав-новесия (в дальнейшем будет использоваться термин "центр атома").
Любое реальное кристаллическое твердое тело всегда имеет некоторое количество каких-либо нарушений в периодическом повторении ато-мов, которые называются дефектами. В кристаллографии наличием дефектов обычно пренебрегают, т.е. рассматривают идеальные кристаллы.
Слайд 9Лекция 1 Слайд 9
Вблизи любой точки аморфного твердого тела также можно выделить
Поэтому аморфное твердое тело характеризуется наличием т.н. ближнего порядка (атомов), но отсутствием дальнего порядка, присущего кристаллам.
Слайд 10Лекция 1 Слайд 10
Наличие периодического повторения атомов
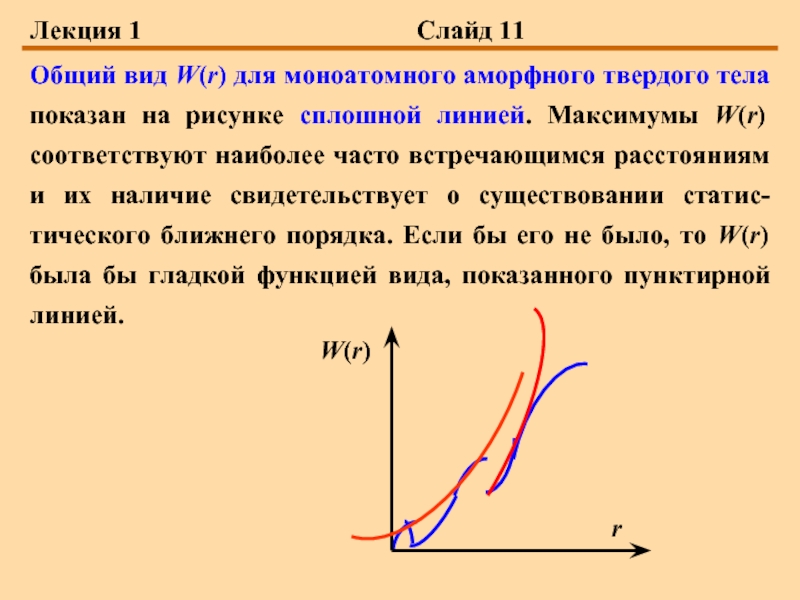
Аморфным твердым телам присущ статистический ближ-ний порядок, суть которого проще всего понять, введя в рас-смотрение функцию радиального распределения атомов W(r).
Для моноатомного твердого тела (имеются атомы только одного элемента) W(r) определяет вероятность нахождения другого атома на расстоянии r от выделенного.
Слайд 11Лекция 1 Слайд 11
Общий вид W(r) для
Слайд 12Лекция 1 Слайд 12
Аморфные материалы в настоящее
Кристаллические твердые тела занимают доминирующее место в окружающем нас материальном мире. Это не только природные горные породы и минералы, но и все металлы, и огромное количество сплавов, которые также являются кристаллическими твердыми телами.
Слайд 13Лекция 1 Слайд 13
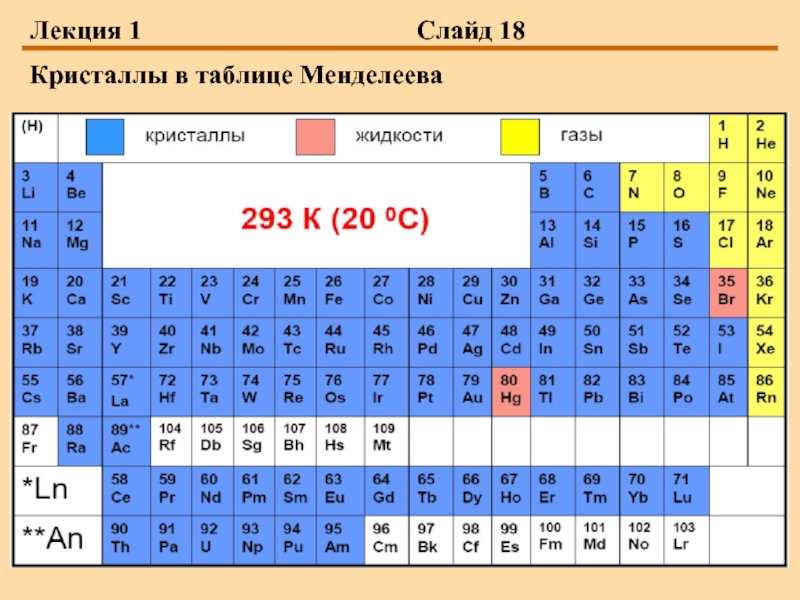
То, что кристалл представляет
Впоследствии, с помощью дифракции рентгеновского излучения, электронов и нейтронов были определены конкретные конфигурации атомов для всех элементов таблицы Менделеева (часть из них переходит в кристаллическое состояние при низких температурах) и огромного количества сплавов. До этого кристаллография базировалась только на визуальных исследованиях геометрических свойств больших природных кристаллов.
Слайд 14Лекция 1 Слайд 14
Результаты таких исследований позволили
С этого момента берет начало кристаллография – наука о геометрическом строении кристаллических твердых тел, в которой все основные положения выводятся исключи-тельно из соображений симметрии без привлечения каких-либо представлений об атомах, образующих кристалл.
Слайд 15Лекция 1 Слайд 15
Термин "кристалл" происходит от
Большие природные кристаллы известны человеку очень давно. Характерными примерами природных кристаллов являются многочисленные разновидности кварца (SiO2), каменной соли (NaCl) и, безусловно, драгоценные камни, такие как рубины (Al2O3) и алмазы.
В данном случае, мы имеем дело с монокристаллами – твердыми телами, у которых элементарная ячейка непрерывно повторяется во всем объеме образца.
Слайд 16Лекция 1 Слайд 16
В XIX веке люди
При искусственном выращивании монокристаллов атомы из окружающей среды отлагаются на его гранях, и грани нарастают параллельно самим себе.
Слайд 17Лекция 1 Слайд 17
Большинство кристаллических твердых тел
В общем случае поликристалл можно рассматривать как большое количество монокристаллических блоков, повер-нутых друг относительно друга на большие углы хаоти-ческим образом. Именно в поликристаллическом состоянии находится подавляющее большинство используемых в нашей жизни, металлов и сплавов.
Слайд 19Лекция 1 Слайд 19
Некоторые соотношения векторной и
Координаты вектора r – коэффициенты разложения вектора по векторам базиса ai (i = 1, 2, 3), r = pa1 + qa2 + ra3.
Скалярное произведение двух векторов a и b – скалярная величина, определяемая в любом базисе выражением
a⋅b = |a||b|cos γ, где γ - угол между векторами a и b
Модуль (абсолютная величина, длина, норма) вектора r есть скалярная величина
Векторное произведение [ab] есть вектор, модуль которого равен
|[ab]| = |a||b| sin γ
Слайд 20Лекция 1 Слайд 20
Смешанное (скалярно-векторное) произведение
a⋅[bc] ≡
[abc]2 = [ab]⋅[[bc][ca]] =
= a2b2c2 – a2(b⋅c)2 – b2(c⋅a)2 – c2(a⋅b)2 + 2(a⋅b)(b⋅c)(c⋅a) =
определитель Грама
Слайд 21Лекция 1 Слайд 21
Тождество Лагранжа [ab]⋅[cd] =
Двойное векторное произведение: [a[bc]] = b(a⋅c) – c(a⋅b)
Решение системы уравнений относительно неизвестного вектора х ([abc] ≠ 0)
Слайд 22Лекция 1 Слайд 22
Элемент матрицы А (aij)
Транспонированная матрица AT – в матрице A (aij) строки заменены столбцами, AT = (aji).
В частности, транспонированная матрица вектора-столбца – матрица вектор-строка.
Слайд 23Лекция 1 Слайд 23
Квадратная матрица:
диагональная – все
единичная I (E) – все элементы главной диагонали равны единице, а все остальные элементы равны нулю, aij = 0 для всех i ≠ j и aij = 1 для всех i = j;
вырожденная (сингулярная) – определитель |A| = detA = 0, понятие определитель имеет смысл только применительно к квадратной матрице.
симметричная, если AT = A.
Слайд 24Лекция 1 Слайд 24
След (шпур) квадратной матрицы
, всегда Tr(A) = Tr(AT).
Произведение двух матриц A⋅B имеет смысл только тогда, когда количество строк матрицы A совпадает с количеством столбцов матрицы B.
В общем случае A⋅B ≠ B⋅A.
Если A⋅B = B⋅A, то матрицы A и B – перестановочные.
Слайд 25Лекция 1 Слайд 25
Обратная матрица для матрицы
АA–1 = A–1А = I.
Понятие обратная матрица имеет смысл только применительно к квадратной матрице.
Если обратная матрица существует, то всегда |A||A-1| = 1.
Для невырожденных матриц (A⋅B)-1 = B-1⋅A-1.
Ортогональная матрица – матрица, у которой
|A| = detA ≠ 0 и AT = A-1.
Слайд 26Лекция 1 Слайд 26
Матричное уравнение вида A⋅X = B
X = A-1⋅B (X = B⋅A-1)
Свойства определителей
detA = detAT
detAB = detAdetB = detBA
detA-1 = (detA)-1 = 1/ detA

















![Лекция 1 Слайд 20Смешанное (скалярно-векторное) произведениеa⋅[bc] ≡ [abc] = [bca] = [cab] =](/img/tmb/1/48009/f0c7199a4262778a89e8a4ada5c26acb-800x.jpg)
![Лекция 1 Слайд 21Тождество Лагранжа [ab]⋅[cd] = (a⋅c)(b⋅d) – (b⋅c)(a⋅d) Двойное векторное произведение:](/img/tmb/1/48009/091a132d2fc70793492bb693f2a5c9bd-800x.jpg)










