Екатеринбург 2014
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Курсовая работа по теоретической механике Динамика кулисного механизма презентация
Содержание
- 1. Курсовая работа по теоретической механике Динамика кулисного механизма
- 2. Расчетная схема и исходные данные Определить: Угловую
- 3. Этап I. Кинематический анализ механизма. Механизм
- 4. Так как
- 5. Угловую скорость катка находим как отношение скорости
- 6. Запись уравнений геометрических связей
- 8. Определение производной кинетической энергии по
- 9. Определение угловой скорости маховика при его
- 10. Определение углового ускорения маховика при его
- 11. Этап III. Реакции связей и уравновешивающая сила.
- 12. Определение силы уравновешивающей кулисный механизм Принцип виртуальных
- 13. Этап IV. Дифференциальное уравнение движения кулисного механизма.
- 14. Уравнение движения машины Машиной называется совокупность
- 15. Полученные результаты
Слайд 1КУРСОВАЯ РАБОТА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
«ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
Студент: Тузов А.Э.
Группа: ММ-230803
Вариант: 23080312
Преподаватель:
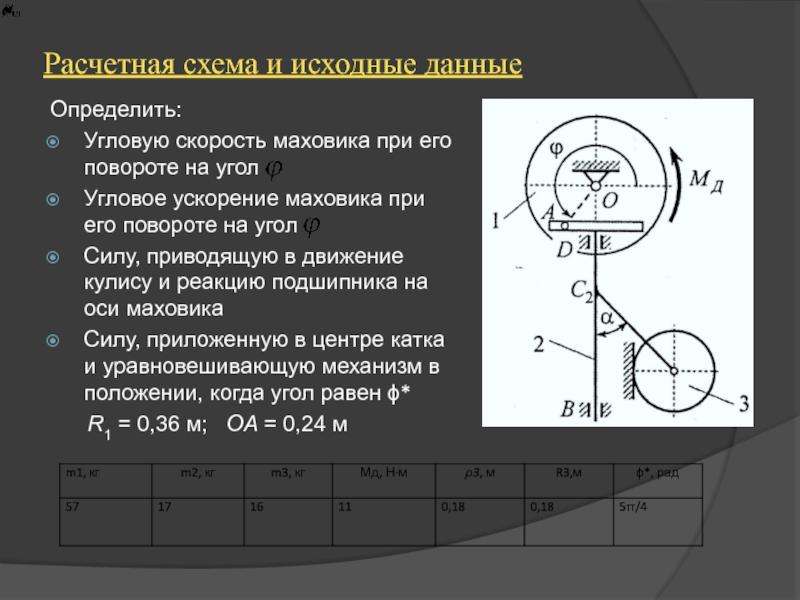
Слайд 2Расчетная схема и исходные данные
Определить:
Угловую скорость маховика при его повороте на
Угловое ускорение маховика при его повороте на угол
Силу, приводящую в движение кулису и реакцию подшипника на оси маховика
Силу, приложенную в центре катка и уравновешивающую механизм в положении, когда угол равен ϕ*
R1 = 0,36 м; OA = 0,24 м
Слайд 3Этап I. Кинематический анализ механизма.
Механизм состоит из трех звеньев. Ведущим
Скорость поступательно движущейся кулисы находим по теореме сложения скоростей, рассматривая движение кулисного камня как сложное.
Слайд 4
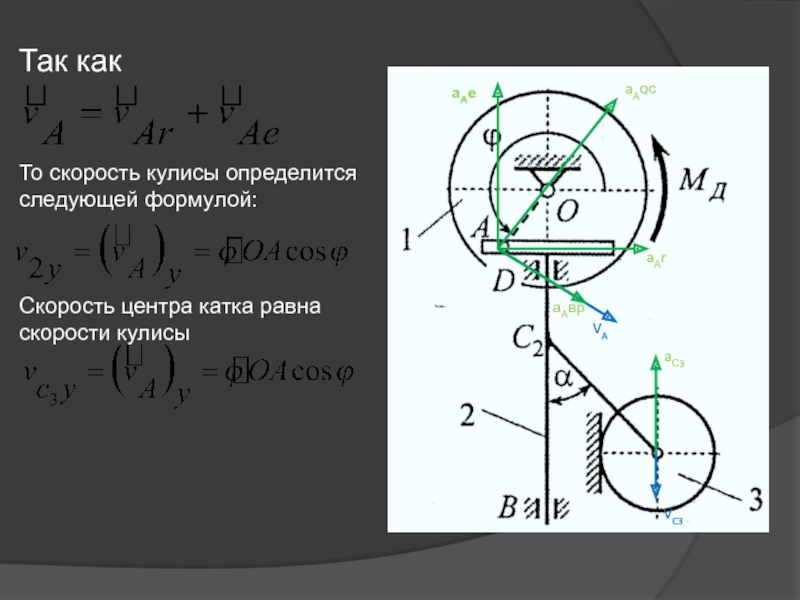
Так как
То скорость кулисы определится следующей формулой:
Скорость центра катка равна
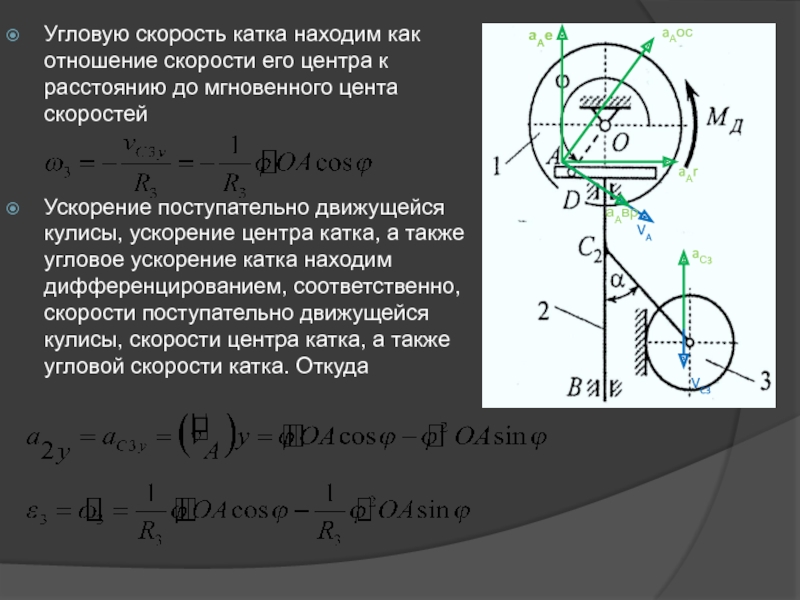
Слайд 5Угловую скорость катка находим как отношение скорости его центра к расстоянию
Ускорение поступательно движущейся кулисы, ускорение центра катка, а также угловое ускорение катка находим дифференцированием, соответственно, скорости поступательно движущейся кулисы, скорости центра катка, а также угловой скорости катка. Откуда
Слайд 7 Этап II. угловая скорость и угловое ускорение маховика. Определение
Кинетическую энергию механизма находим как сумму кинетических энергий его звеньев
-кинетическая энергия вращающегося маховика
-кинетическая энергия поступательно движущейся кулисы
-кинетическая энергия катка, совершающего плоское движение
Кинетическая энергия системы после тождественных преобразований:
Слайд 8
Определение производной кинетической энергии по времени
Определение элементарной работы, мощности внешних сил.
Мощность
Работа при повороте маховика на угол
Слайд 9
Определение угловой скорости маховика при его повороте на угол φ*
Для определения
Подстановка в это равенство найденных выражений дает:
Тогда
Слайд 10
Определение углового ускорения маховика при его повороте на угол φ*. Воспользуемся
Определим угловое ускорение маховика при угле его поворота φ*:
Слайд 11Этап III. Реакции связей и уравновешивающая сила.
Определим реакцию подшипника на
Маховик совершает вращательное движении. Рассмотрим внешние силы. Помимо пары сил с моментом , на него действуют реакция подшипника и реакция кулисы . Система сил инерции приводится к паре с моментом , направленным против вращения, т.к. оно ускоренное.
Записывая условие уравновешенности плоской системы внешних сил, находим
Слайд 12Определение силы уравновешивающей кулисный механизм
Принцип виртуальных перемещений: Для равновесия механической системы
Используя уравнения связей
находим вариации координат
Подстановка этих соотношений в уравнение принципа виртуальных перемещений дает
Слайд 13Этап IV. Дифференциальное уравнение движения кулисного механизма.
Уравнение Лагранжа второго рода
Составим дифференциальное
Подстановка найденных значений в уравнение Лагранжа дает
Слайд 14Уравнение движения машины
Машиной называется совокупность твердых тел (звеньев), соединенных между собой
Запишем дифференциальное уравнение движения машины
Дифференциальные уравнения движения механизма, полученные с помощью теоремы
об изменении кинетической энергии, уравнения Лагранжа и уравнения движения
машины совпадают.