Лекция 6
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Курс Ядерная энергетика и атомные реакторы. Лекция 6. Замедление нейтронов. Кинематика презентация
Содержание
- 1. Курс Ядерная энергетика и атомные реакторы. Лекция 6. Замедление нейтронов. Кинематика
- 2. Система центра масс Принцип относительности Галилея.
- 3. Полагаем mn=1 Если инерциальная система 2
- 4. В системе С нейтрон и ядро движутся
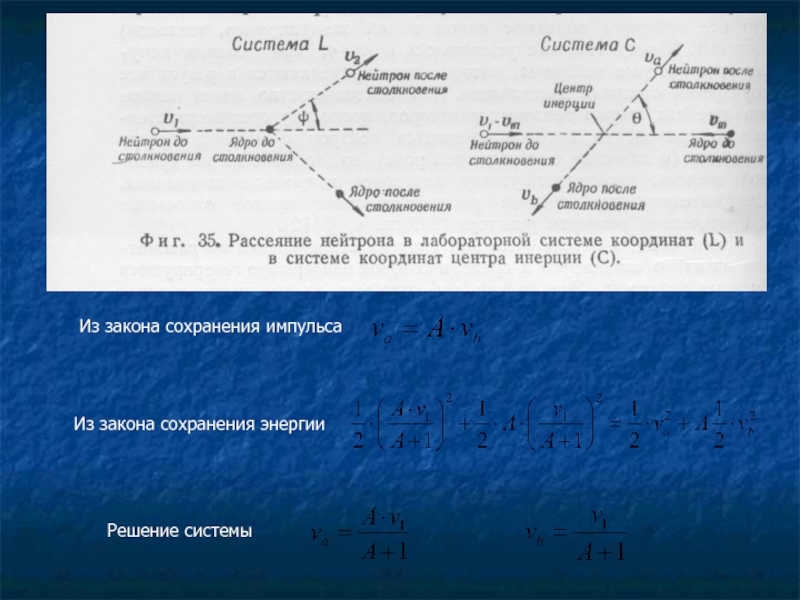
- 5. Из закона сохранения импульса Из закона сохранения энергии Решение системы
- 6. Энергия нейтрона после соударения
- 7. Изменение энергии нейтрона при рассеянии Энергия нейтрона
- 8. Максимальная потеря энергии Максимальная потеря энергии нейтрона
- 9. Скользящий удар, Θ=0 – соответствует неизменной энергии
- 10. Закон рассеяния В системе центра инерции рассеяние
- 11. Используя значение производной Получаем
- 12. Проверка правильности распределения
- 13. Асимметрия рассеяния в лабораторной системе Из рис.
- 14. Резонансы при замедлении нейтронов. Формула Брейта - Вигнера
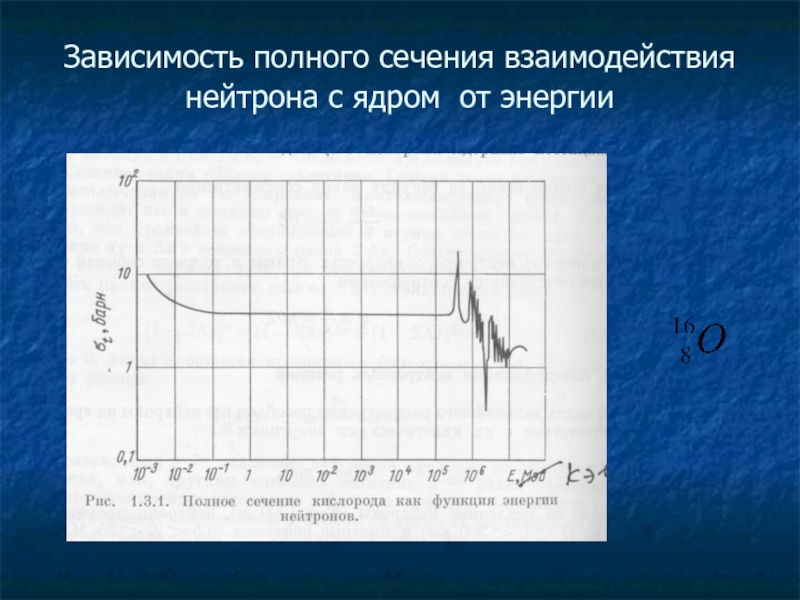
- 15. Зависимость полного сечения взаимодействия нейтрона с ядром от энергии
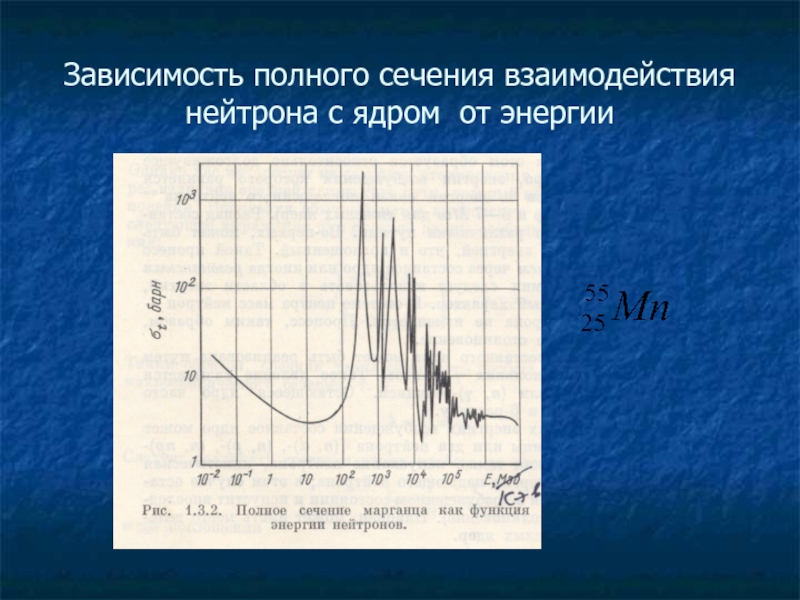
- 16. Зависимость полного сечения взаимодействия нейтрона с ядром от энергии
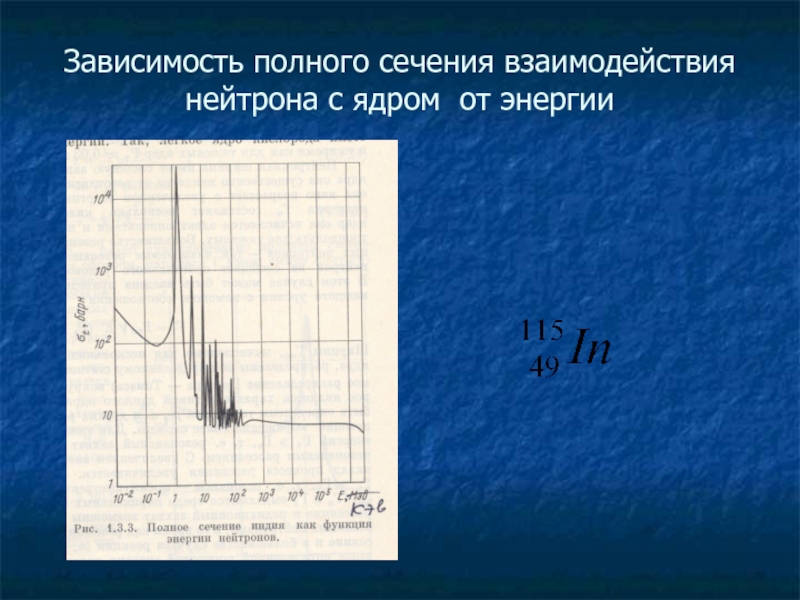
- 17. Зависимость полного сечения взаимодействия нейтрона с ядром от энергии
- 18. Ширины резонансов Для
- 19. Для тепловых нейтронов с энергией E=0.04 эв
- 20. Формула Брейта-Вигнера Для медленных и промежуточных
- 21. Получить выражения: 3.
Система центра масс Принцип относительности Галилея. Если импульс сохраняется в одной инерциальной системе, то он сохраняется и в любой другой системе, движущейся относительно нее с произвольной скоростью
Слайд 1Замедление нейтронов.
Кинематика.
М.А. Киселёв
Курс «Ядерная энергетика и атомные реакторы»
ДУ, 15 октября
2014
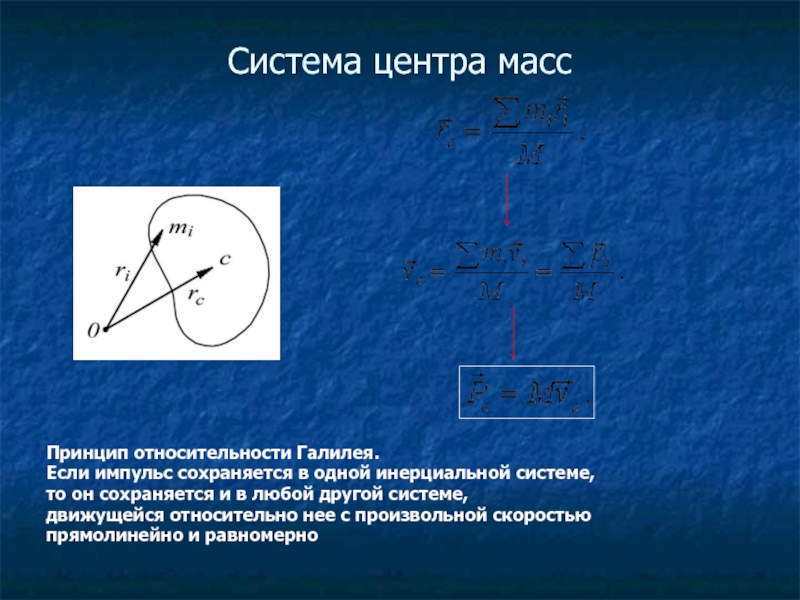
Слайд 2Система центра масс
Принцип относительности Галилея.
Если импульс сохраняется в одной инерциальной
системе,
то он сохраняется и в любой другой системе,
движущейся относительно нее с произвольной скоростью
прямолинейно и равномерно
то он сохраняется и в любой другой системе,
движущейся относительно нее с произвольной скоростью
прямолинейно и равномерно
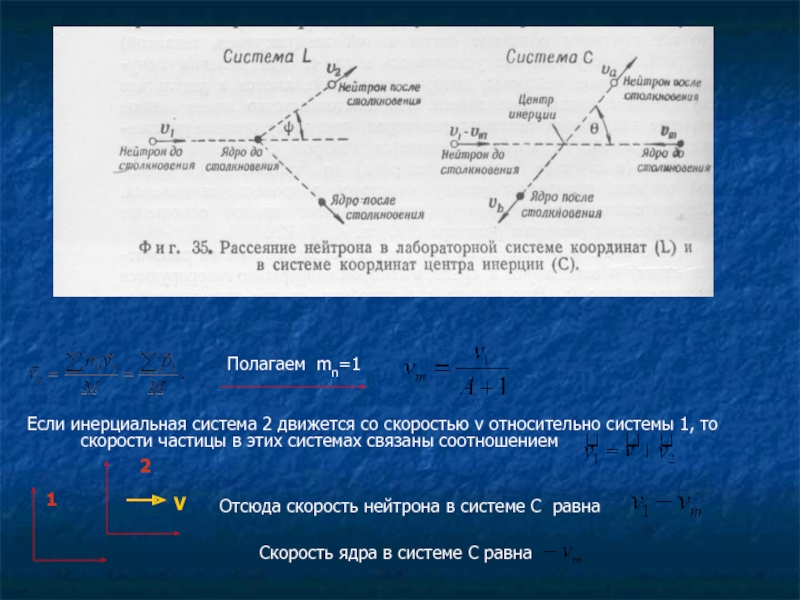
Слайд 3
Полагаем mn=1
Если инерциальная система 2 движется со скоростью v относительно системы
1, то скорости частицы в этих системах связаны соотношением
2
1
Отсюда скорость нейтрона в системе С равна
Скорость ядра в системе С равна
V
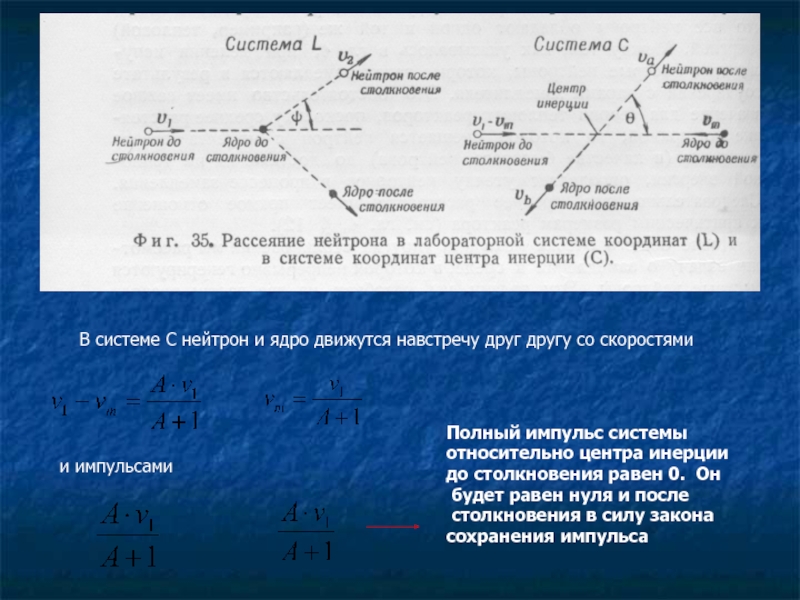
Слайд 4В системе С нейтрон и ядро движутся навстречу друг другу со
скоростями
и импульсами
Полный импульс системы
относительно центра инерции
до столкновения равен 0. Он
будет равен нуля и после
столкновения в силу закона
сохранения импульса
Слайд 7Изменение энергии нейтрона при рассеянии
Энергия нейтрона до рассеяния
Энергия нейтрона после
рассеяния
Определим
(*)
Слайд 8Максимальная потеря энергии
Максимальная потеря энергии нейтрона происходит при θ=π
Разлагая в ряд
по степеням 1/А
Для A ≥50
Слайд 9Скользящий удар, Θ=0 – соответствует неизменной энергии
нейтрона до и после
соударения
Лобовой удар, Θ=π – соответствует максимальной потери энергии
нейтроном. Потеря энергии будет зависеть от атомного номера
ядра рассеивателя.
Слайд 10Закон рассеяния
В системе центра инерции рассеяние нейтронов сферически
симметрично для нейтронов
с энергией меньше нескольких Мэв
Вероятность того, что нейтрон рассеялся под углом Θ
Вероятность того, что нейтрон рассеялся с энергией E2
где Е2 и Θ связаны соотношением
Отсюда определяем dE2/dΘ
Слайд 11
Используя значение производной
Получаем
Учитывая, что
Получаем, что распределение нейтронов по энергиям не зависит
от конечной энергии и определяется значением максимальной
потери энергии
потери энергии
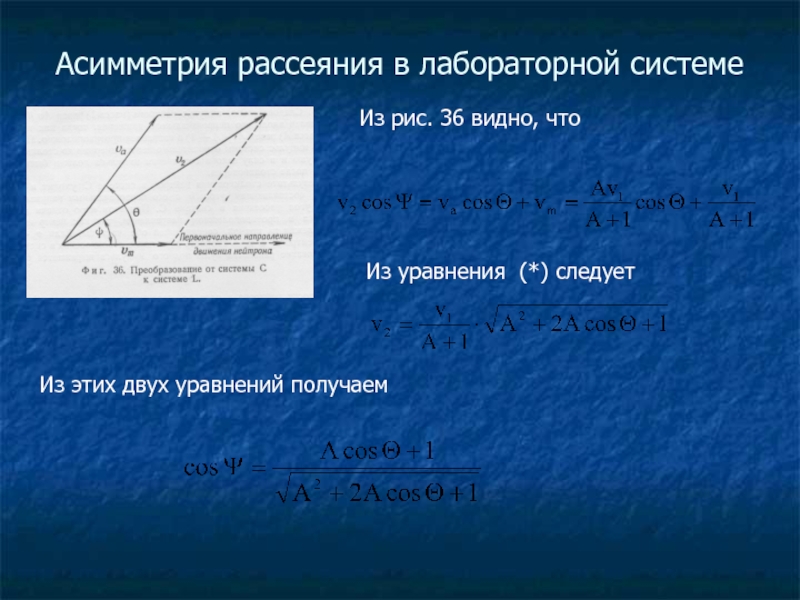
Слайд 13Асимметрия рассеяния в лабораторной системе
Из рис. 36 видно, что
Из уравнения (*)
следует
Из этих двух уравнений получаем
Слайд 19Для тепловых нейтронов с энергией E=0.04 эв
время пролета ядра урана составляет
6⋅10-18 сек.
Такому времени пролета соответствует ширина
уровня
Такому времени пролета соответствует ширина
уровня
Для медленных и промежуточных нейтронов
Слайд 20Формула Брейта-Вигнера
Для медленных и промежуточных нейтронов
с учетом этого получаем закон
Общий
случай
где x=γ, α, n, f
Слайд 21Получить выражения:
3. Посчитать dE2/dΘ
1.
2.
4. Доказать, что
для тяжелых ядер углы рассеяния нейтрона
в лабораторной системе и в системе центра масс совпадают.
в лабораторной системе и в системе центра масс совпадают.
5. Получить выражение для элемента телесного угла dΩ
