- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конвекция. Основные положения переноса теплоты. (Тема 2. Лекции 6,7) презентация
Содержание
- 1. Конвекция. Основные положения переноса теплоты. (Тема 2. Лекции 6,7)
- 2. § 1. Основные положения
- 3. Если перенос теплоты осуществляется за счет хаотического
- 4. Чем резче меняется температура, тем интенсивнее происходит
- 5. коэффициент температуропроводности, характеризующий интенсивность молекулярного переноса теплоты.
- 6. Существует аналогия между молекулярным переносом импульса (трением
- 7. Так как плотность потока массы равна
- 8. В случае конвективной теплоотдачи плотность теплопотока на
- 9. Скорость жидкости на поверхности обтекаемого ею тела
- 10. Если известно распределение температуры вблизи поверхности и
- 11. § 3. Дифференциальное уравнение энергии Фурье–Кирхгофа
- 12. В неподвижной системе координат выделим элементарный объем
- 13. Через противоположную грань выходит dQX+dX
- 14. Повторяя эти рассуждения для осей y и
- 15. Подставив сюда выражение для суммарной величины плотности
- 16. Перенося второе слагаемое правой части уравнения влево,
- 17. Рассмотрим неограниченный стационарный ламинарный поток жидкости с
- 18. По мере удаления от кромки поверхности толщина
- 19. Охлаждение цилиндра в потоке. Интерферометр Маха-Цендера демонстрирует
- 20. Плоский конвективный факел, поднимающийся
Слайд 2§ 1. Основные положения
Теплоотдача – процесс теплообмена в двухфазной системе на границе раздела фаз (например, теплообмен между продуктами сгорания топлива и поверхностью металлических заготовок, нагреваемых в печи).
Теплопередача – процесс теплообмена между двумя средами, разделенными твердой перегородкой (например, теплообмен между дымом и нагреваемым воздухом через стенку теплообменника).
Процесс переноса теплоты характеризуется вектором плотности теплового потока , проекция которого на нормаль к некоторой поверхности представляет собой количество теплоты, проходящее через единицу этой поверхности за единицу времени, Вт/м2.
Слайд 3Если перенос теплоты осуществляется за счет хаотического теплового движения или тепловых
Если перенос теплоты в движущейся жидкости или газе осуществляется за счет перемещения объемов среды из области с одной температурой в область с другой температурой, то такой процесс называют конвекцией тепла.
Перенос тепла излучением (радиационный теплообмен) осуществляется в результате распространения электромагнитных волн.
Различают три вида теплообмена.
Слайд 4Чем резче меняется температура, тем интенсивнее происходит процесс теплопроводности. На этом
,
где λ, Вт/(м⋅К) – коэффициент теплопроводности, физический параметр вещества, характеризующий его способность проводить теплоту. Зависит от температуры, а для газов (кроме инертных) – также и от давления.
Жан Батист Жозеф Фурье (1768–1830) – французский математик и физик. В 1807 и 1811 годах он представил Парижской АН свои открытия по теории распространения теплоты в твердом теле, а в 1822 году опубликовал работу «Аналитическая теория тепла».
Слайд 5 коэффициент температуропроводности, характеризующий интенсивность молекулярного переноса теплоты.
Будем считать, что плотность и
Тогда закон Фурье можно представить в виде:
,
Введем обозначение
, м2/c –
где , Дж/м3 – объемная энтальпия, т. е. количество теплоты, содержащееся в единице объема вещества с температурой Т).
Слайд 6Существует аналогия между молекулярным переносом импульса (трением в ламинарном потоке) и
(§ 3 темы 1) и ,
что плотность потока обеих субстанций (импульса и теплоты) пропорциональна градиенту объемной плотности соответствующей субстанции (импульса и энтальпии), а коэффициентом пропорциональности является коэффициент переноса, имеющий размерность м2/c.
Слайд 7Так как плотность потока массы равна ,
.
Процесс конвективного теплопереноса тесно связан с молекулярным переносом теплоты. Следовательно, суммарная величина плотности теплопотока в движущейся теплопроводной жидкости
.
§ 2. Основные понятия конвективного теплопереноса
Слайд 8В случае конвективной теплоотдачи плотность теплопотока на поверхности определяется по формуле
,
где α, Вт/(м2⋅К) – коэффициент теплоотдачи,
Т0 и ТW – температура жидкости и поверхности.
Плотность теплопотока на поверхности зависит от:
скорости и направления движения жидкости;
режима движения;
температуры потока и температуры поверхности;
физических свойств жидкости (прежде всего от λ);
формы и качества поверхности твердого тела.
Вся сложность процесса теплоотдачи учитывается коэффициентом α, который зависит от тех же факторов, что и величина qW.
Слайд 9Скорость жидкости на поверхности обтекаемого ею тела равна нулю, следовательно, перенос
На основании закона сохранения энергии можно приравнять плотность теплопотока на поверхности, найденную из постулата Фурье и по формуле Ньютона. В результате получим дифференциальное уравнение конвективной теплоотдачи:
,
где n – координата, направленная по нормали к поверхности, n = 0 соответствует точке на поверхности;
λ – коэффициент теплопроводности жидкости;
ΔT = T0 – TW – температурный напор.
Слайд 10Если известно распределение температуры вблизи поверхности и заданы величины ΔT и
.
Знаком «–» пренебрегают, так как α принято считать величиной положительной.
Дифференциальное уравнение конвективной теплоотдачи позволяет получить формулу для коэффициента теплоотдачи, которая дает возможность найти эту величину.
Фото «Разливка стали. Урал».
Автор – Георгий Розов
Слайд 11§ 3. Дифференциальное уравнение энергии Фурье–Кирхгофа
Густав Роберт Кирхгоф (1824–1887) –
Рассмотрим поток несжимаемой жидкости (ρ=const) с произвольным распределением температуры T(x,y,z,t) и скорости. Считаем, что скорость невелика, то есть нет выделения теплоты из-за вязкого трения; отсутствуют внутренние источники теплоты, и теплофизические свойства жидкости – постоянны.
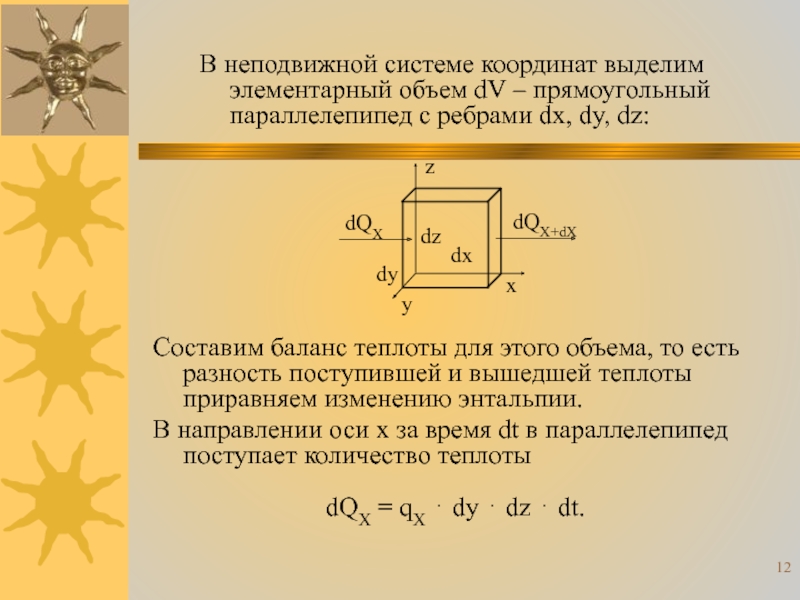
Слайд 12В неподвижной системе координат выделим элементарный объем dV – прямоугольный параллелепипед
Составим баланс теплоты для этого объема, то есть разность поступившей и вышедшей теплоты приравняем изменению энтальпии.
В направлении оси x за время dt в параллелепипед поступает количество теплоты
dQX = qX ⋅ dy ⋅ dz ⋅ dt.
Слайд 13Через противоположную грань выходит
dQX+dX = qX+dX ⋅ dy ⋅ dz
где проекция вектора плотности теплопотока на ось х для правой грани находится путем разложения в ряд Тейлора (ограничиваемся первыми двумя слагаемыми этого ряда):
.
Разность между поступившим в параллелепипед количеством теплоты и вышедшим из него составит
.
Слайд 14Повторяя эти рассуждения для осей y и z, и суммируя полученные
.
С другой стороны, изменение энтальпии в жидкости в объеме dV за время dt составит
.
Приравнивая, получим:
.
Слайд 15Подставив сюда выражение для суммарной величины плотности теплопотока, переносимого конвекцией
.
Разделим на ρ⋅сP, распишем и учтем, что
:
.
Процесс теплопереноса обусловлен двумя механизмами: переносом за счет молекулярной теплопроводности и чисто конвективным переносом из-за перемещения теплоты вместе с движущейся жидкостью.
Слайд 16Перенося второе слагаемое правой части уравнения влево, получим слева субстанциальную производную
Учтем также, что в соответствии с уравнением неразрывности для несжимаемой жидкости (§ 4 темы 1).
Получим окончательно:
,
или:
.
Слайд 17Рассмотрим неограниченный стационарный ламинарный поток жидкости с постоянной температурой T0, направленный
Из-за теплообмена приповерхностных слоев жидкости с поверхностью их температура изменяется.
Тепловым пограничным слоем называется тонкая по сравнению с размерами потока зона, в пределах которой имеется градиент температуры и вызванный наличием этого градиента перенос теплоты поперек потока за счет молекулярной теплопроводности (при ламинарном режиме).
§ 4. Тепловой пограничный слой
Слайд 18По мере удаления от кромки поверхности толщина погранслоя нарастает, так как
Соотношение толщин гидродинамического и теплового погранслоев должно зависеть от соответствующих коэффициентов переноса:
~ –
критерий Прандтля.
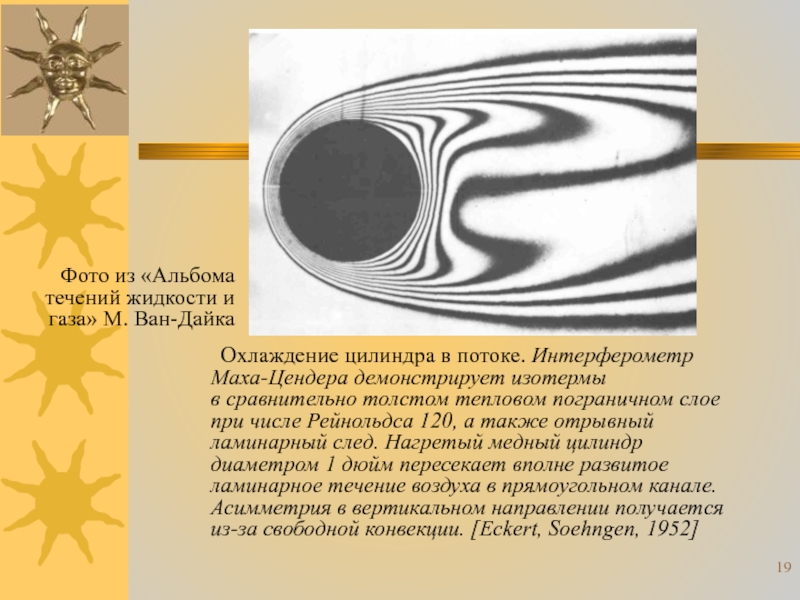
Слайд 19 Охлаждение цилиндра в потоке. Интерферометр Маха-Цендера демонстрирует изотермы
Фото из «Альбома течений жидкости и газа» М. Ван-Дайка
Слайд 20 Плоский конвективный факел, поднимающийся от
Фото из «Альбома течений жидкости и газа» М. Ван-Дайка