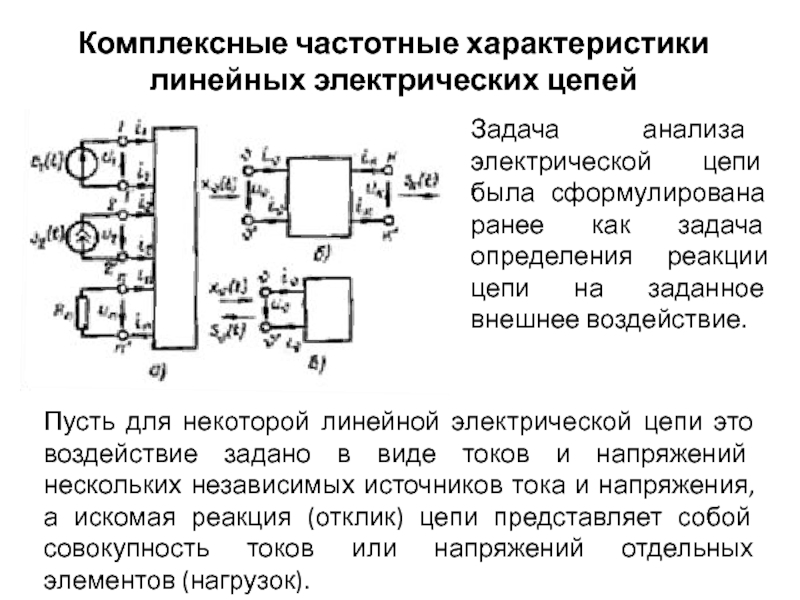
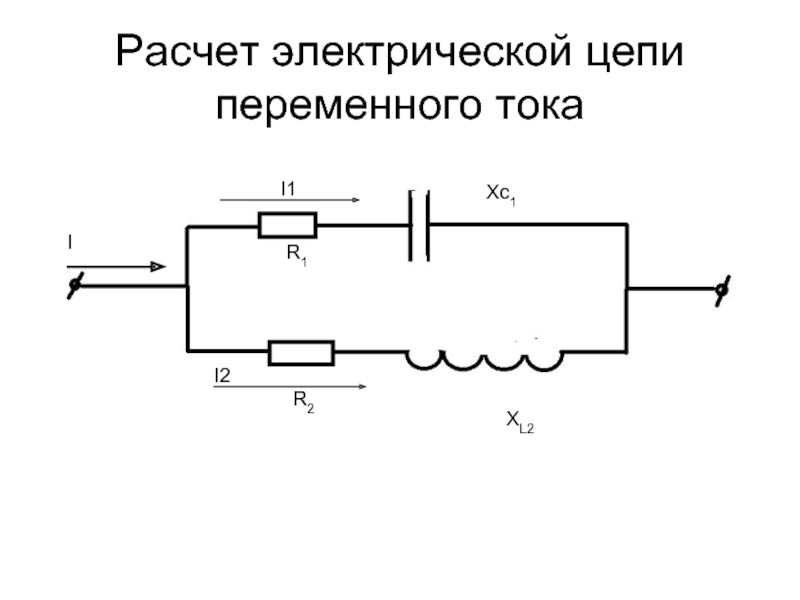
Пусть для некоторой линейной электрической цепи это воздействие задано в виде токов и напряжений нескольких независимых источников тока и напряжения, а искомая реакция (отклик) цепи представляет собой совокупность токов или напряжений отдельных элементов (нагрузок).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные частотные характеристики линейных электрических цепей презентация
Содержание
Слайд 1
Комплексные частотные характеристики линейных электрических цепей
Задача анализа электрической цепи была сформулирована
Слайд 2
Комплексные частотные характеристики линейных электрических цепей
Вынесем из рассматриваемой цепи ветви, содержащие
Входными будем называть пару зажимов (полюсов), к которым подключается каждый из независимых источников, задающих внешнее воздействие на цепь.
Зажимы, служащие для подключения нагрузки, т. е. ветви, ток или напряжение которой необходимо определить, назовем выходными.
Слайд 3
Комплексные частотные характеристики линейных электрических цепей
Стороной многополюсника или портом называется пара
Из определений входных и выходных зажимов следуют важные особенности зажимов, образующих порт многополюсника:
− ток, втекающий через один зажим порта, равен току, вытекающему через другой зажим этого же порта;
− между парами полюсов, принадлежащих к разным портам, не должно быть никаких внешних по отношению к многополюснику соединений (внутри многополюсника соединения естественно могут быть).
Слайд 4
Комплексные частотные характеристики линейных электрических цепей
Зажимы, образующие одну сторону многополюсника, обозначим
Пусть внешнее воздействие на цепь задано только на одной паре полюсов v-v’: x(t)=xv(t) и необходимо найти реакцию цепи также только на одной паре полюсов k-k’: s(t)=sk(t).
Исследуемую цепь удобно рассматривать как двусторонний четырехполюсник. Если v=k, то цепь становится односторонней, т. е. превращается в двухполюсник.
Слайд 5
Комплексные частотные характеристики линейных электрических цепей
Ограничимся рассмотрением случая гармонического внешнего воздействия;
По определению, комплексной частотной характеристикой (частотным коэффициентом передачи) цепи называется отношение комплексных изображений отклика и воздействия:
Слайд 6
Комплексные частотные характеристики линейных электрических цепей
Размерность комплексной частотной характеристики (КЧХ) равна
- сопротивления (внешнее воздействие − iv, реакция цепи − uk), - проводимости (внешнее воздействие − uv, реакция цепи − ik) или быть безразмерной (внешнее воздействие − iv, реакция цепи − ik, либо внешнее воздействие − uv, реакция цепи − uk).
Слайд 7
Комплексные частотные характеристики линейных электрических цепей
Как и всякое комплексное число, КЧХ
или алгебраической
форме.
Представляя комплексные изображения отклика и воздействия в показательной форме
определяем модуль и аргумент КЧХ:
Слайд 8
Комплексные частотные характеристики линейных электрических цепей
Таким образом, модуль КЧХ равен отношению
КЧХ цепи численно равна комплексной амплитуде реакции цепи на воздействие, описываемое единичной гармонической функцией, т. е. на воздействие гармонического тока или выражения с единичной амплитудой и нулевой начальной фазой.
Слайд 9
Комплексные частотные характеристики линейных электрических цепей
Зависимости модуля Hkv(ω) и аргумента ψkv(ω)
АЧХ и ФЧХ цепи характеризуют зависимости от частоты соответственно амплитуды и начальной фазы отклика цепи на внешнее воздействие с Xmv=1 и ψx=0 .
Слайд 10
Комплексные частотные характеристики линейных электрических цепей
Комплексные частотные характеристики цепи делятся на
Когда отклик и внешнее воздействие рассматриваются на одних и тех же зажимах цепи, КЧХ называется входной.
Если отклик и внешнее воздействие задаются на разных зажимах цепи, КЧХ называется передаточной.
Слайд 11
Комплексные частотные характеристики линейных электрических цепей
Различают два вида входных и четыре
Слайд 15
Комплексные частотные характеристики идеализированных двухполюсных элементов
Сопротивление. Комплексное входное сопротивление резистивного элемента
Модуль комплексного входного сопротивления ZR(ω) и его аргумент ϕR(ω) не зависят от частоты:
поэтому АЧХ и ФЧХ комплексного входного сопротивления имеют вид прямых линий с постоянной ординатой.
Слайд 16
Комплексные частотные характеристики идеализированных двухполюсных элементов
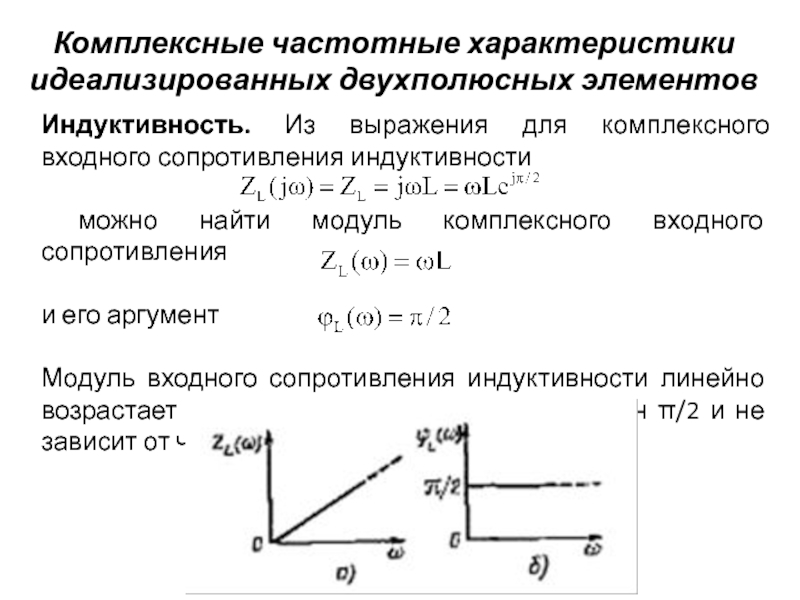
Индуктивность. Из выражения для комплексного входного
можно найти модуль комплексного входного сопротивления
и его аргумент
Модуль входного сопротивления индуктивности линейно возрастает с ростом частоты, а аргумент равен π/2 и не зависит от частоты.
Слайд 17
Комплексные частотные характеристики идеализированных двухполюсных элементов
Емкость. Комплексное входное сопротивление емкости, как
модуль комплексного входного сопротивления емкости и его аргумент равны
модуль входного сопротивления емкости уменьшается и стремится к нулю при ω→∞, а аргумент равен -π/2 и не зависит от частоты.
Слайд 19
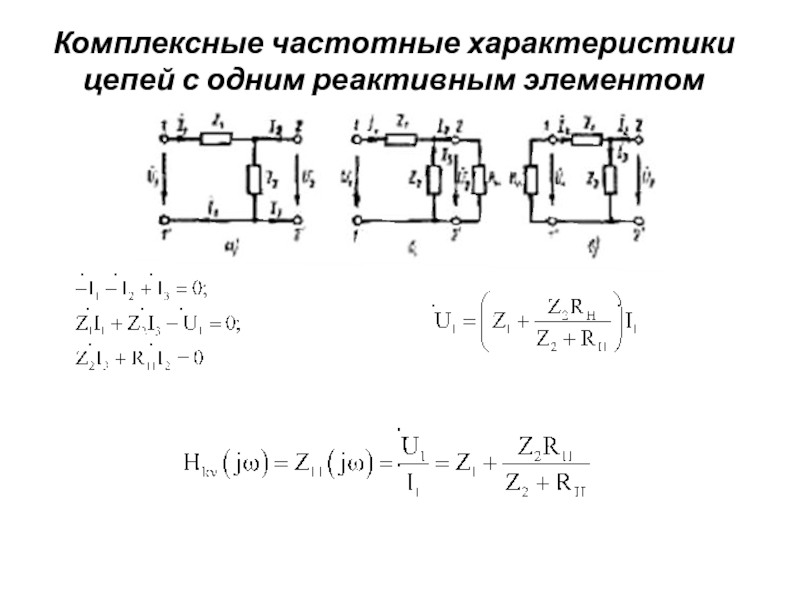
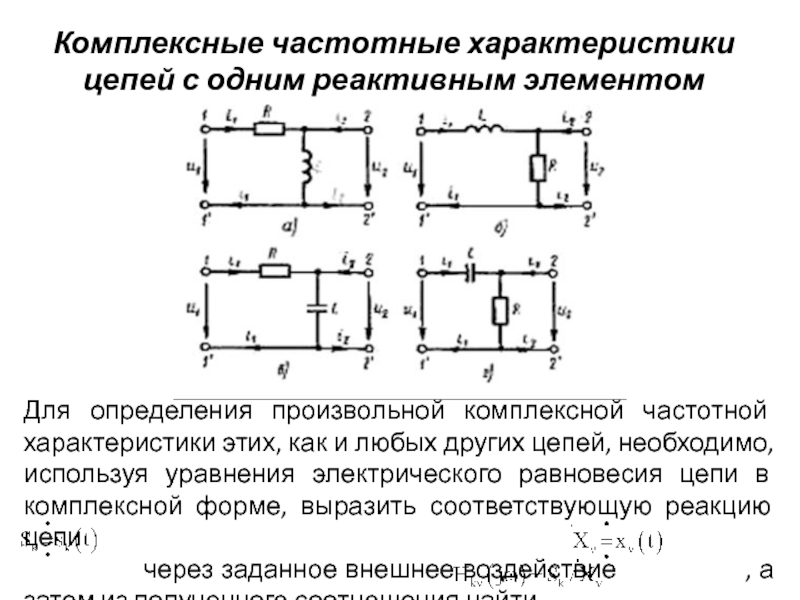
Комплексные частотные характеристики цепей с одним реактивным элементом
Для определения произвольной комплексной
через заданное внешнее воздействие , а затем из полученного соотношения найти .