- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Колебания и волны. Гармонические колебания презентация
Содержание
- 1. Колебания и волны. Гармонические колебания
- 2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Виды и признаки колебаний В
- 3. о Fв = −kx - возвращающая сила,
- 4. Любая колебательная система, в которой возвращаю-щая
- 5. 2. Параметры гармонических колебаний Расстояние груза
- 6. Т – период колебаний – минимальный
- 7. Колебания характеризуются не только смещением х,
- 8. 3. Механические гармонические колебания (на примере маятников)
- 9. Рассмотрим случай а)– пружинный маятник. Второй
- 10. Потенциальная энергия ( пружинный маятник):
- 11. г) физический маятник Физический маятник –
- 12. Сравнивая с уравнением свободных незатухающих гармонических
- 13. Свободные гармонические колебания в электрическом колебательном
- 14. 4. Способы представления гармонических колебаний Гармонические
- 15. 5. Сложение гармонических колебаний одного направления
- 16. 1) Разность фаз равна нулю или
- 17. Когерентными называются колебания, разность фаз которых
- 19. Вообще, колебания вида x = A(t)cos[ωt
- 20. 6. Сложение взаимно перпендикулярных колебаний Пусть
- 21. Возведем обе части в квадрат,
- 22. Рассмотрим частные случаи решения уравнения (6.7)
- 23. 7. Свободные затухающие механические колебания Все
- 24. Однородное дифференциальное уравнение второго по-рядка, описывающее
- 25. Натуральный логарифм отно-шения амплитуд, следующих друг
- 26. Следовательно, коэффициент затухания β есть физи-ческая
Слайд 2ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Виды и признаки колебаний
В физике особенно выделяют колебания двух видов
Колебательным движением называются процес-сы, отличающиеся той или иной степенью повто-ряемости во времени.
Для колебаний характерно превращение одного вида энергии в другой – кинетической в потенциальную, магнитной в электрическую и т.д.
Простейшим примером периодического движения служат колебания груза на конце пружины.
Будем считать, что массой пружины можно пренебречь и что пружина установлена горизонтально.
Слайд 3о
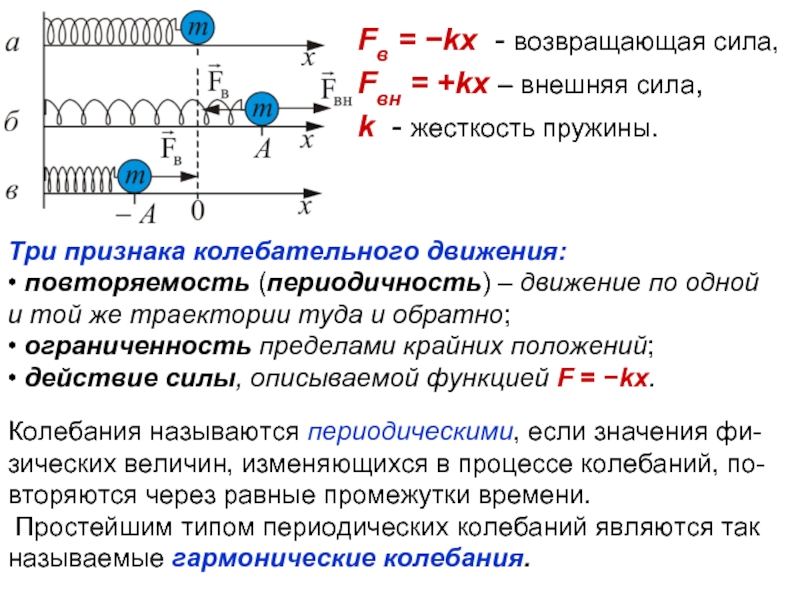
Fв = −kx - возвращающая сила,
Fвн = +kx – внешняя сила,
k
Три признака колебательного движения:
• повторяемость (периодичность) – движение по одной и той же траектории туда и обратно;
• ограниченность пределами крайних положений;
• действие силы, описываемой функцией F = −kx.
Колебания называются периодическими, если значения фи-зических величин, изменяющихся в процессе колебаний, по-вторяются через равные промежутки времени.
Простейшим типом периодических колебаний являются так называемые гармонические колебания.
Слайд 4
Любая колебательная система, в которой возвращаю-щая сила прямо пропорциональна смещению, взятому
Саму такую систему часто называют гармоническим осциллятором.
1) Колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
2)Различные периодические процессы можно пред-ставить как наложение гармонических колебаний.
Периодический процесс можно описать уравнением:
f(t) = f (t + nT) .
По определению, колебания называются гармоничес-кими, если зависимость некоторой величины x = f (t) имеет вид
x = Asin φ или x = Acosφ (6.1)
Здесь синус или косинус используются в зависимости от условия задачи, А и φ – параметры колебаний.
Слайд 5
2. Параметры гармонических колебаний
Расстояние груза от положения равновесия до точки, в
Максимальное смещение – наибольшее расстояние от положения равновесия – называется амплитудой и обо-значается буквой A.
Выражение, стоящее под знаком синуса или косинуса в формуле (6.1) φ = ωt + φ0 , определяет смещение x в дан-ный момент времени t и называется фазой колебания.
При t =0 φ = φ0, поэтому φ0 называется начальной фазой колебания. Фаза измеряется в радианах и определяет зна-чение колеблющейся величины в данный момент времени.
Движение от некоторой начальной точки до возвращения в ту же точку, например от x = A к x = −A и обратно в x = A, называется полным колебанием.
Частота колебаний ν определяется как число полных колебаний в 1 секунду. Частоту, как правило, измеряют в герцах (Гц): 1 Гц равен 1 полному колебанию в секунду.
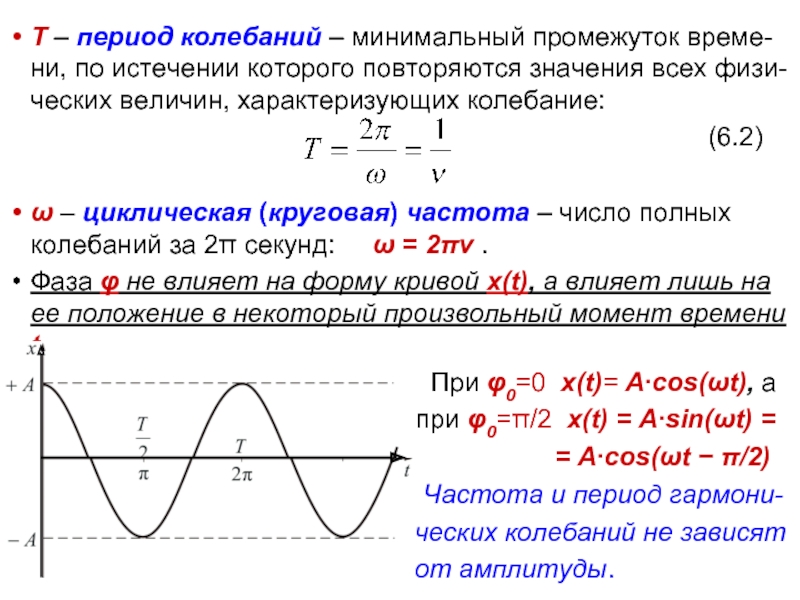
Слайд 6
Т – период колебаний – минимальный промежуток време-ни, по истечении которого
(6.2)
ω – циклическая (круговая) частота – число полных колебаний за 2π секунд: ω = 2πν .
Фаза φ не влияет на форму кривой х(t), а влияет лишь на ее положение в некоторый произвольный момент времени t.
При φ0=0 x(t)= A∙cos(ωt), а
при φ0=π/2 x(t) = A∙sin(ωt) =
= A∙cos(ωt − π/2)
Частота и период гармони-
ческих колебаний не зависят
от амплитуды.
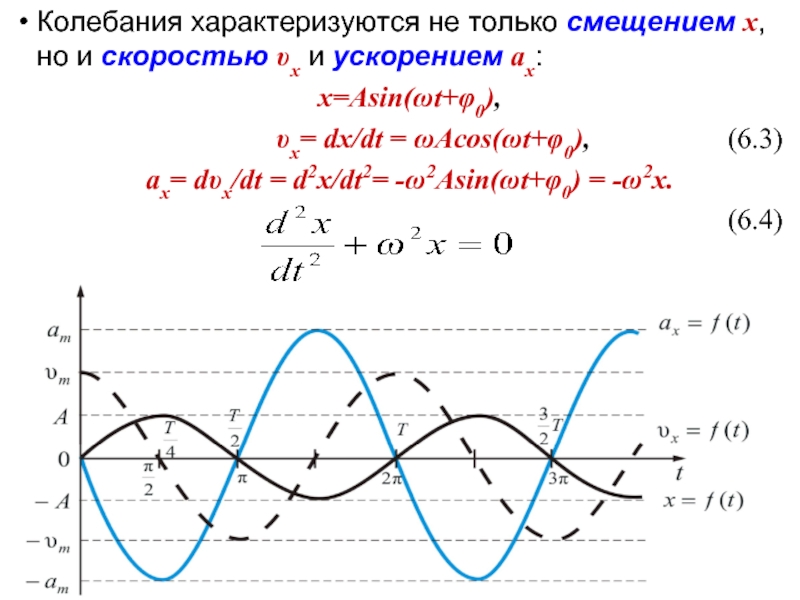
Слайд 7
Колебания характеризуются не только смещением х, но и скоростью υx и
x=Asin(ωt+φ0),
υx= dx/dt = ωAcos(ωt+φ0), (6.3)
ax= dυx/dt = d2x/dt2= -ω2Asin(ωt+φ0) = -ω2x.
(6.4)
Слайд 83. Механические гармонические колебания (на примере маятников)
Если физическую систему, обладающую состоянием
Способную совершать собственные колебания систему называют осциллятором. Примером линейных (одномерный случай) ос-цилляторов могут служить маятники (рис.): а) пружинный (груз на пружине); б) крутильный (диск на проволоке); в) математи-ческий (материальная точка на нерастяжимой нити); г) физический (С – центр масс твердого тела, О – точка прохождения оси коле-баний, перпендикулярной плоскости чертежа).
Слайд 9
Рассмотрим случай а)– пружинный маятник.
Второй закон Ньютона для колеблющегося тела для
x = Xmax∙cos(ω0t +φ0)
Система, совершающая колебания под действием квазиупругой си-лы , называется линейным гармоническим осциллятором (ЛГО).
Кинетическая энергия материальной точки (колеблющегося тела):
Слайд 10
Потенциальная энергия ( пружинный маятник):
Полная механическая энергия:
Классическая колеблющаяся точка не может
Колебания Wk и Wn совершаются со сдвигом по фазе на π и, следо-вательно, полная механическая энергия материальной точки при свободных незатухающих гармонических колебаниях не изменяется со временем (const).
Слайд 11
г) физический маятник
Физический маятник – твердое тело, которое может совершать колебания
При отклонении маятника на угол α момент,
создаваемый силой тяжести равен:
M = mgd sinα .
Согласно основному уравнению динамики
вращательного движения (для тела с момен-
том инерции I, вращающегося вокруг непод-
вижной оси в отсутствие трения):
При малых α → sinα ≈ α →
Слайд 12
Сравнивая с уравнением свободных незатухающих гармонических колебаний: d2x/dt2 + ω2x =
Предельным случаем физического маятника является математичес-кий маятник - материальная точка, подвешенная на невесомой не-растяжимой нити и совершающая колебания в вертикальной пло-скости под действием силы тяжести. Вся масса сосредоточена в центре масс тела. При этом d=l – длина маятника и момент инер-ции J = ml2. Тогда
Длина математического маятника, имеющего такой же период ко-лебаний, что и данный физический маятник, называется приве-денной длиной физического маятника. Точка О1, находящаяся на расстоянии lпр от точки подвеса О маятника, называется центром качания физического маятника. Точки O и О1 обладают свойством взаимности, т.е. при перемене их ролей длина и период маятника останутся прежними.
Слайд 13
Свободные гармонические колебания в электрическом
колебательном контуре
Простейшим колебательным контуром является замкнутая цепь,
состоящая
По закону Ома для замкнутой цепи: сумма падений
напряжений на проводниках сопротивлением R и на
конденсаторе Uс равна ЭДС самоиндукции в контуре
IR + Uc = IR + Q/C = εsi = -L(dI/dt).
I = dQ/dt → dI/dt = d2Q/dt2,
(R→0) → d2Q/dt2 + ω2Q =0
Q =Qmsin(ωt + φ0) и I = dQ/dt = ωQmcos(ωt + φ0) = Imcos(ωt + φ0)
W = Wэл + Wмагн = (1/2)∙(LI2 + CU2)
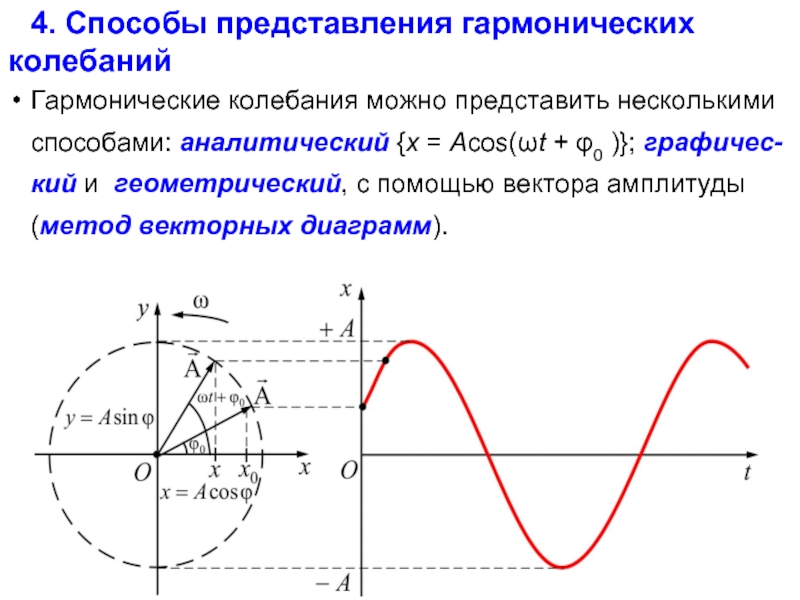
Слайд 14
4. Способы представления гармонических колебаний
Гармонические колебания можно представить несколькими способами: аналитический
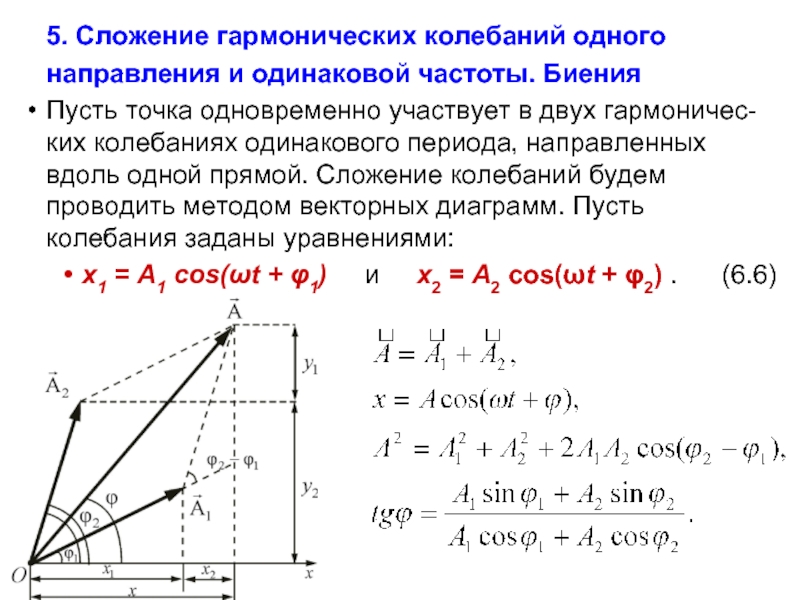
Слайд 15
5. Сложение гармонических колебаний одного
направления и одинаковой частоты. Биения
Пусть точка одновременно
x1 = A1 cos(ωt + φ1) и x2 = A2 cos(ωt + φ2) . (6.6)
Слайд 16
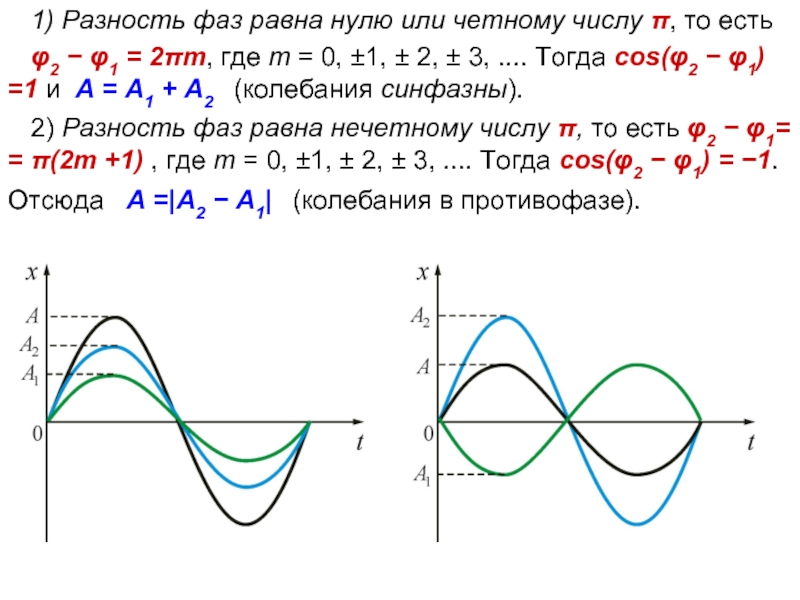
1) Разность фаз равна нулю или четному числу π, то есть
φ2
2) Разность фаз равна нечетному числу π, то есть φ2 − φ1= = π(2m +1) , где m = 0, ±1, ± 2, ± 3, .... Тогда cos(φ2 − φ1) = −1. Отсюда A =|A2 − A1| (колебания в противофазе).
Слайд 17
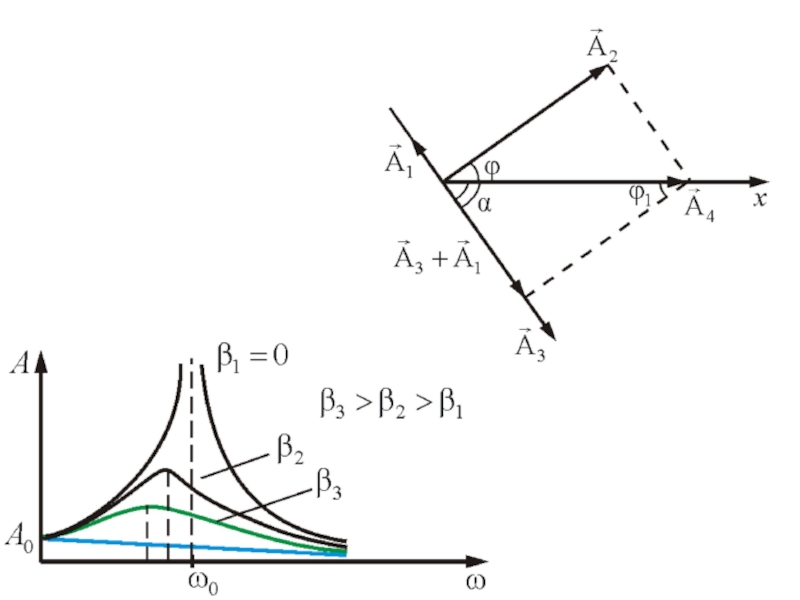
Когерентными называются колебания, разность фаз которых во времени постоянна; т.к. ∆Ф(t)
А амплитуда и Ф=(ωt+ϕ) фаза результирующего колебания. Тогда в зависимости от значения (ϕ2 −ϕ1) результирующая амплитуда А изменяется в пределах от A = |A1 − A2| при ϕ2 -ϕ1 = ±(2m +1)π, до A = |A1 + A2| при ϕ2 -ϕ1 = ±2 π m (m → целые числа).
При ϕ2 -ϕ1 = ±2 π m колебания называются синфазными (в одной фазе), а при ϕ2 -ϕ1 = ±(2m +1)π – противофазными.
При ω1 ≠ ω2 результирующий вектор A будет изменяться по длине и вращаться с переменной скоростью. При сложении колебаний с близкими частотами (Δω=|ω2 −ω1|<<ω) возникают, так называе-мые, биения, тогда x1 = Acosωt, x2 = Acos(ωt + Δωt).
Слайд 18
[2ωt >>Δω; cos(-Δωt)=cos(Δωt)]
Косинус берется по модулю, так как функция четная и поэтому частота биений ωб = Δω, а не Δω/2. Период биений равен поло-вине периода модуляции:
Тб = Тмод /2 = 2π/(Δω)
Слайд 19
Вообще, колебания вида x = A(t)cos[ωt + φ(t)] называются модулированными. Частные
Любые сложные периодические колебания S=f (t) можно представить в виде суперпозиции одновременно совершаю-щихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными цикличес-кой частоте ω:
Представление периодической функции в таком виде связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье (то есть представление сложных модулированных колебаний в виде ряда (суммы) простых гармонических колебаний). Слагаемые ряда Фурье, определяющие гармонические колебания с ча-стотами ω, 2ω, 3ω, ..., называются первой (или основной), второй, третьей и т.д. гармониками сложного периодического колебания.
Слайд 20
6. Сложение взаимно перпендикулярных колебаний
Пусть некоторое тело колеблется и вдоль оси
Найдем уравнение результирующего колебания. Для прос-тоты примем ω1 = ω2 = ω. Разность фаз между обоими коле-баниями равна: Δφ = φ2 − φ1 . Чтобы получить уравнение траектории, надо исключить из этих уравнений время t.
Упростим выражения, выбрав начало отсчета так, чтобы
φ1 = 0 , т.е. x = A1 cosωt ; y = A2 cos(ωt + Δφ) .
или
Слайд 21
Возведем обе части в квадрат, сгруппируем и получим окончательное уравнение:
(6.7)
В результате
Слайд 22
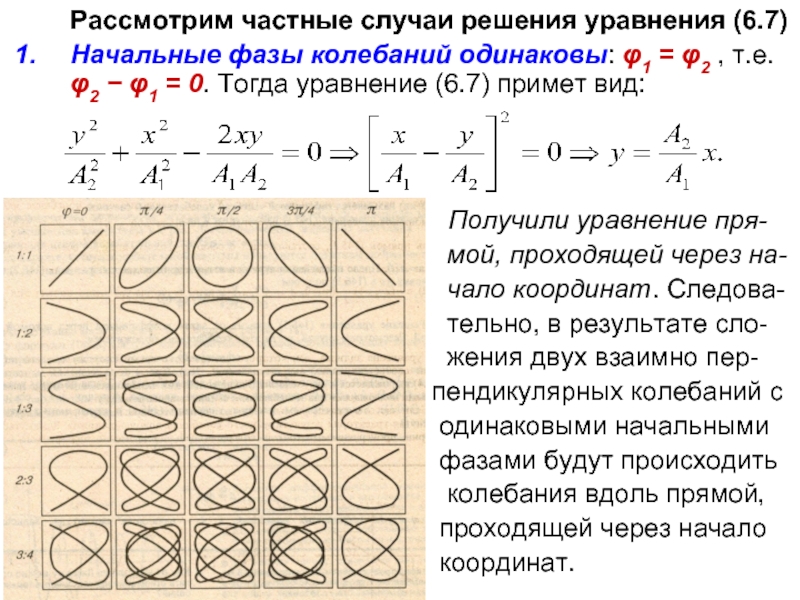
Рассмотрим частные случаи решения уравнения (6.7)
Начальные фазы колебаний одинаковы: φ1 =
Получили уравнение пря-
мой, проходящей через на-
чало координат. Следова-
тельно, в результате сло-
жения двух взаимно пер-
пендикулярных колебаний с
одинаковыми начальными
фазами будут происходить
колебания вдоль прямой,
проходящей через начало
координат.
Слайд 23
7. Свободные затухающие механические колебания
Все реальные колебания являются затухающими. Энергия механических
где r – коэффициент сопротивления, v – скорость движения.
Слайд 24
Однородное дифференциальное уравнение второго по-рядка, описывающее затухающее колебательное дви-жение, запишется в
Решение этого уравнения имеет вид:
Здесь А0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения.
где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний.
Слайд 25
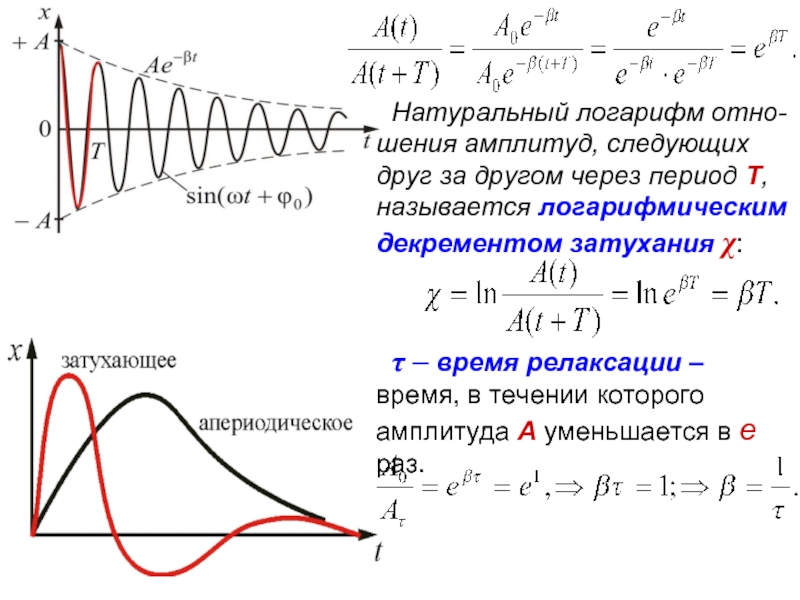
Натуральный логарифм отно-шения амплитуд, следующих друг за другом через период Т,
τ – время релаксации – время, в течении которого амплитуда А уменьшается в е раз.
Слайд 26
Следовательно, коэффициент затухания β есть физи-ческая величина, обратная времени, в течение
Пусть N число колебаний, после которых амплитуда умень-шается в e раз. Тогда:
τ = NТ; → T = τ/N; →β = 1/τ
Следовательно, логарифмический декремент затуха-ния χ есть физическая величина, обратная числу колеба-ний, по истечении которых амплитуда А уменьшается в e раз.











![[2ωt >>Δω; cos(-Δωt)=cos(Δωt)]Косинус берется по модулю, так как функция](/img/tmb/2/115119/bbcd9523565f4cfc3c446825e2fe31ce-800x.jpg)
![Вообще, колебания вида x = A(t)cos[ωt + φ(t)] называются модулированными. Частные случаи: амплитудная моду-ляция и](/img/tmb/2/115119/abf267230a23849d73bbd620a76e1a43-800x.jpg)