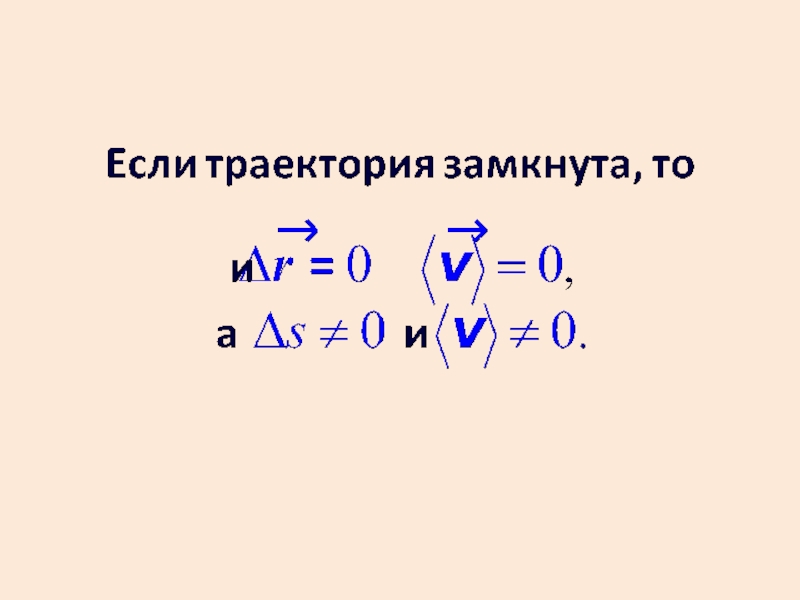- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кинематика. Операции с векторами презентация
Содержание
- 1. Кинематика. Операции с векторами
- 2. Физика изучает наиболее общие законы формирования и
- 4. “Пусть будет стыдно тому, кто бездумно пользуется
- 5. МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ Операции с векторами
- 6. 1. Обозначение вектора
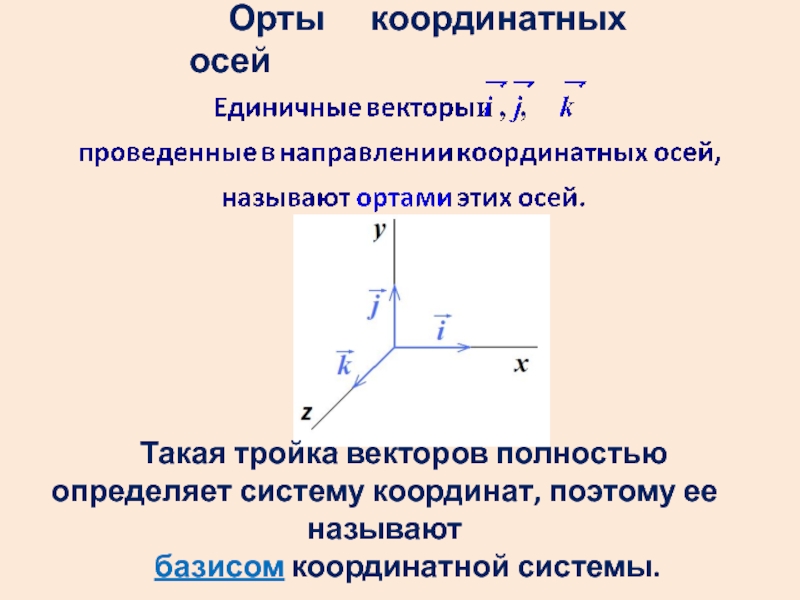
- 7. Орты координатных осей Такая тройка векторов полностью
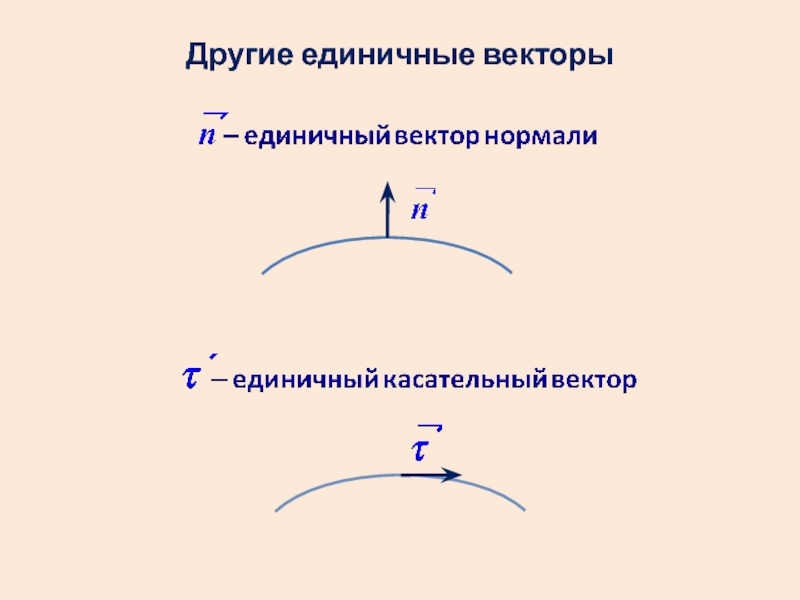
- 8. Другие единичные векторы
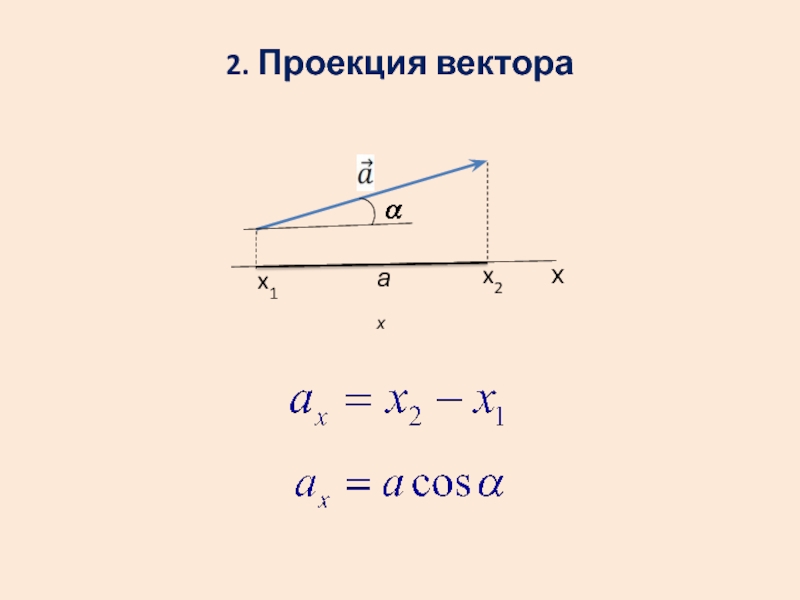
- 9. 2. Проекция вектора х ах x2 x1
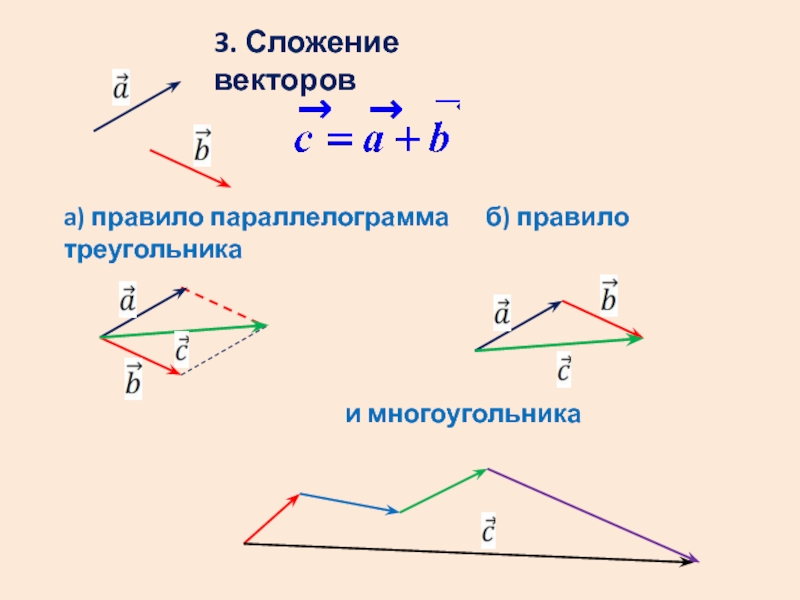
- 10. 3. Сложение векторов a) правило параллелограмма
- 11. 4. Умножение вектора на число
- 12. 5. Разложение вектора через проекции х y z
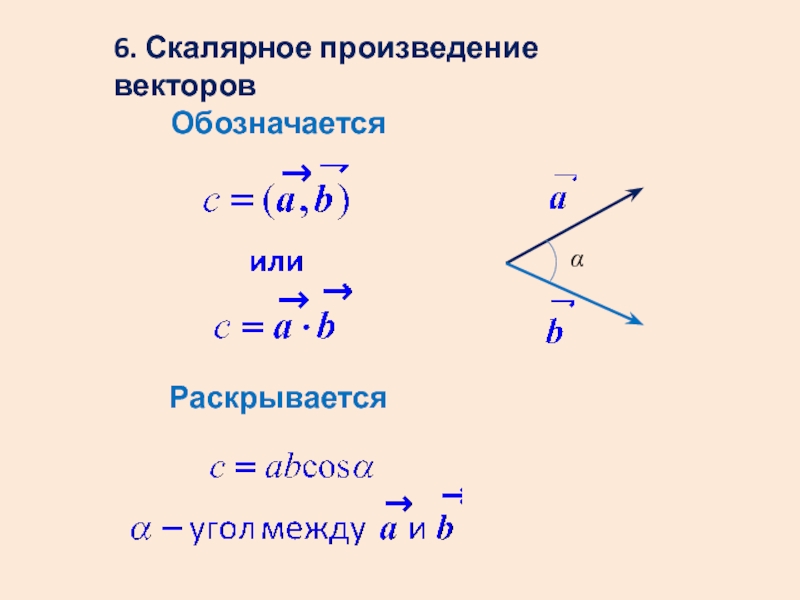
- 13. 6. Скалярное произведение векторов Обозначается Раскрывается α
- 14. Примеры
- 15. 7. Векторное произведение векторов Обозначается Раскрывается
- 16. Вектор направлен по нормали к
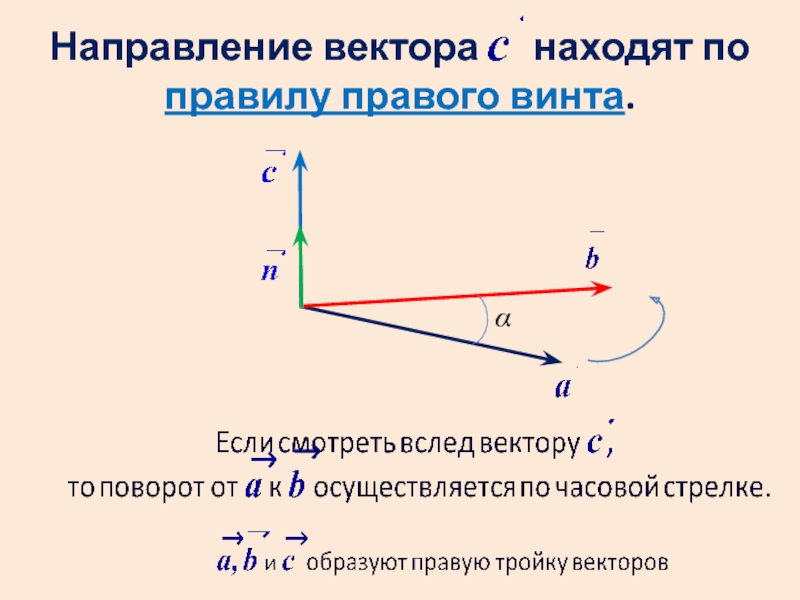
- 17. Направление вектора находят по правилу правого винта. α
- 18. Примеры
- 19. 8. Производная вектора
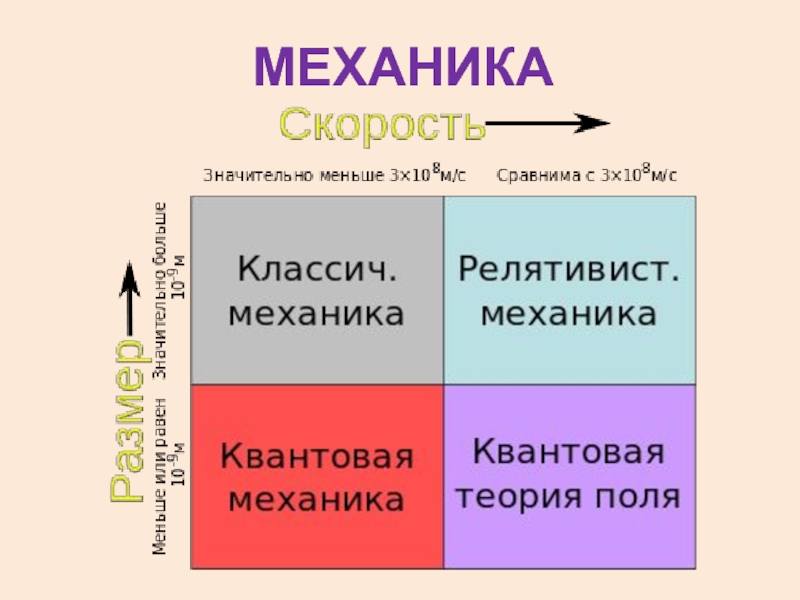
- 20. МЕХАНИКА
- 21. Механика изучает движение тел. Механическое движение –
- 22. За тело отсчета принимают такое тело, которое
- 23. Основная задача механики- – зная положение
- 24. Реальные физические явления очень сложны и, как
- 25. Материальная точка – – тело,
- 26. ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение
- 27. Траектория – линия, по которой движется материальная
- 28. траектория Радиус-вектор – это вектор, проведенный из начала координат в данную точку траектории.
- 31. Путь и модуль вектора перемещения равны только
- 32. СКОРОСТЬ Скорость – это величина, характеризующая быстроту изменения радиус-вектора материальной точки со временем.
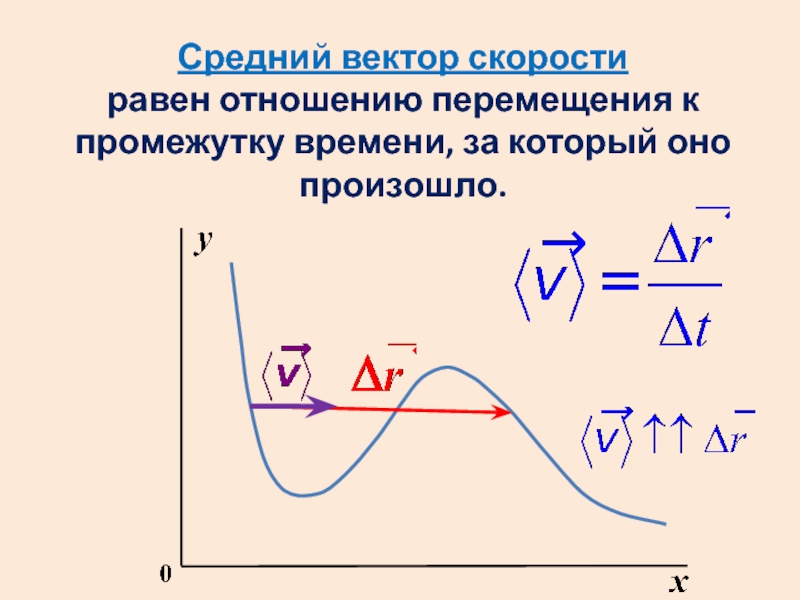
- 33. Средний вектор скорости равен отношению
- 34. Средняя путевая скорость (средний модуль скорости) равна
- 36. Мгновенная скорость – это скорость в данный
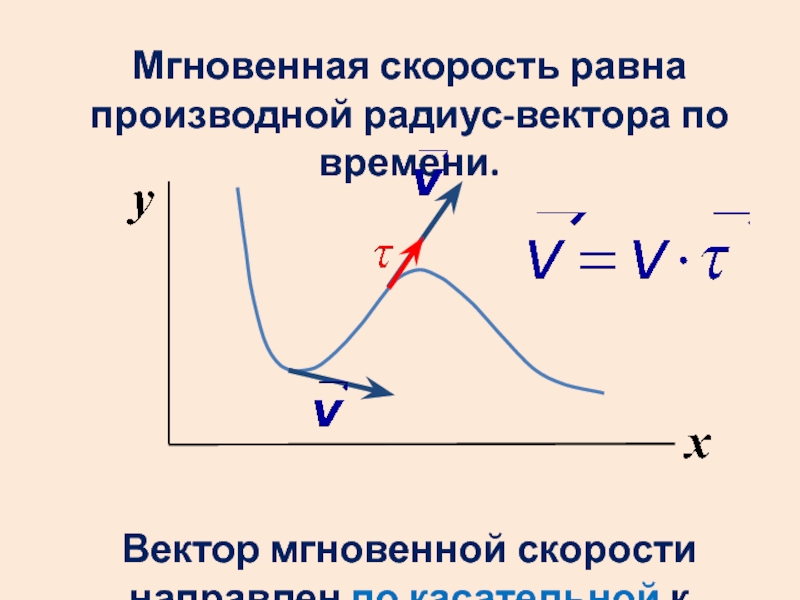
- 37. Мгновенная скорость равна производной радиус-вектора по времени.
- 38. Модуль мгновенной скорости находят как производную пути по времени.
- 39. Нахождение пути по заданной скорости
- 40. Путь, пройденный за время от t1
Физика изучает наиболее общие законы формирования и развития окружающей нас материи в ее наиболее примитивных формах, которые принято называть неживой природой. Поэтому можно утверждать, что физика является фундаментом
Слайд 2Физика изучает наиболее общие законы формирования
и развития окружающей нас материи в
ее наиболее примитивных формах,
которые принято называть неживой природой.
Поэтому можно утверждать, что физика является фундаментом всех естественных наук.
которые принято называть неживой природой.
Поэтому можно утверждать, что физика является фундаментом всех естественных наук.
Слайд 4“Пусть будет стыдно тому, кто бездумно пользуется чудесами науки и техники,
смысля в них не более того, что смыслит в ботанике корова, с удовольствием щиплющая траву.”
(А. Эйнштейн, 1903 г.)
(А. Эйнштейн, 1903 г.)
Слайд 7Орты координатных осей
Такая тройка векторов полностью определяет систему координат, поэтому ее
называют
базисом координатной системы.
базисом координатной системы.
Слайд 16Вектор направлен по нормали к плоскости, в которой лежат
векторы . Он перпендикулярен обоим векторам-сомножителям.
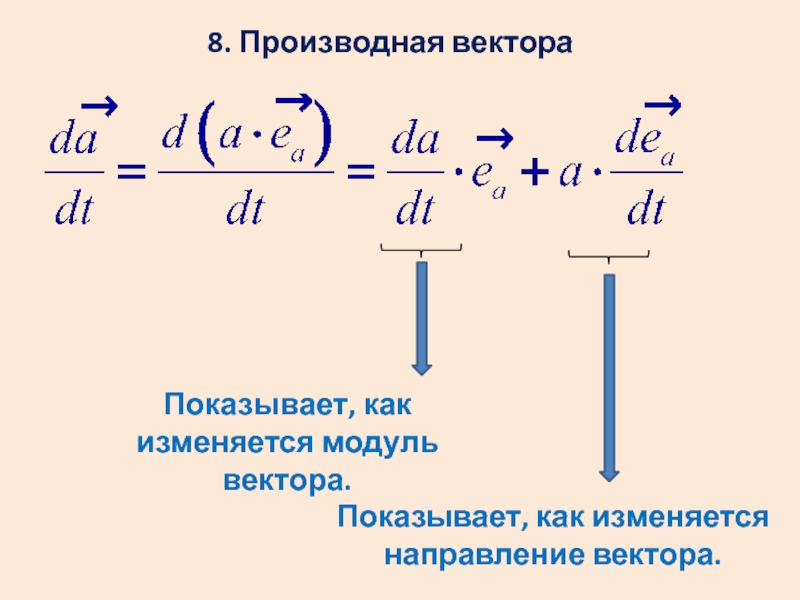
Слайд 198. Производная вектора
Показывает, как изменяется модуль вектора.
Показывает, как изменяется направление вектора.
Слайд 21Механика изучает движение тел.
Механическое движение – изменение положения тела относительно других
тел.
Для описания движения необходима система отсчёта: тело отсчёта, система координат, часы.
Для описания движения необходима система отсчёта: тело отсчёта, система координат, часы.
Слайд 22За тело отсчета принимают такое тело, которое в данной задаче можно
условно считать неподвижным.
Тело отсчета
Слайд 23Основная задача механики-
– зная положение и скорость тела в начальный
момент времени, определить положение и скорость тела в произвольный момент времени.
Слайд 24Реальные физические явления очень сложны и, как правило, возможно лишь приближенное
их описание.
Для этого пользуются упрощающими моделями.
Для этого пользуются упрощающими моделями.
Слайд 25
Материальная точка –
– тело, размерами и формой которого в данной
задаче можно пренебречь.
(Массой – нельзя!)
Абсолютно твердое тело –
– такое тело, деформацией которого можно пренебречь.
(Массой – нельзя!)
Абсолютно твердое тело –
– такое тело, деформацией которого можно пренебречь.
Слайд 26ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Поступательное движение – все точки тела движутся одинаково.
Любая прямая, связанная с телом, параллельна самой себе.
Достаточно описать движение одной точки.
Вращательное движение – точки тела движутся по окружностям, центры которых лежат на неподвижной прямой, называемой осью вращения.
Достаточно описать движение одной точки.
Вращательное движение – точки тела движутся по окружностям, центры которых лежат на неподвижной прямой, называемой осью вращения.
Слайд 27Траектория – линия, по которой движется материальная точка.
Положение точки на траектории
можно задать либо с помощью координат х, y, z, либо с помощью радиус–вектора .
Кинематика материальной точки
Слайд 28
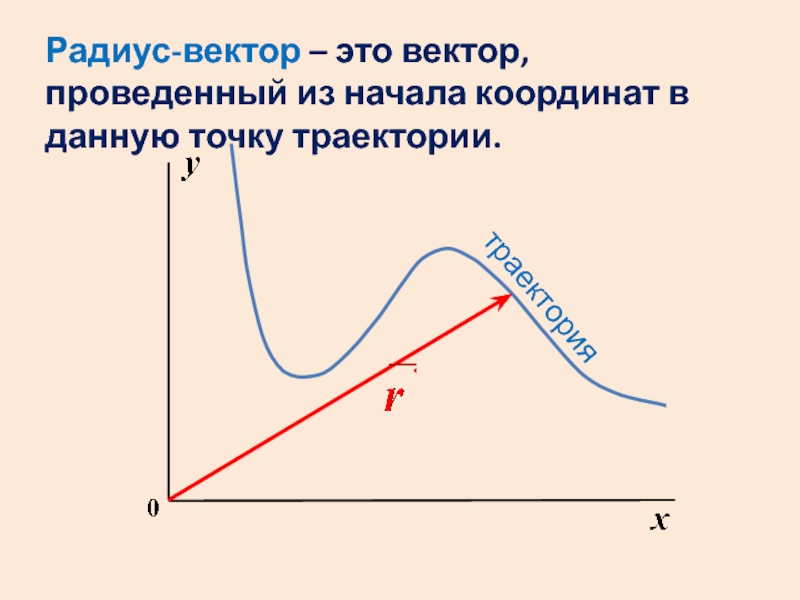
траектория
Радиус-вектор – это вектор, проведенный из начала координат в данную точку
траектории.
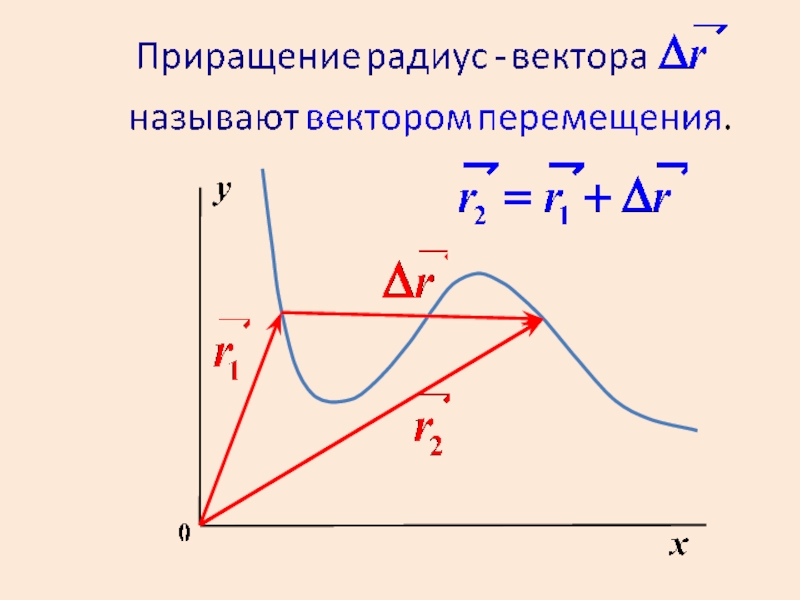
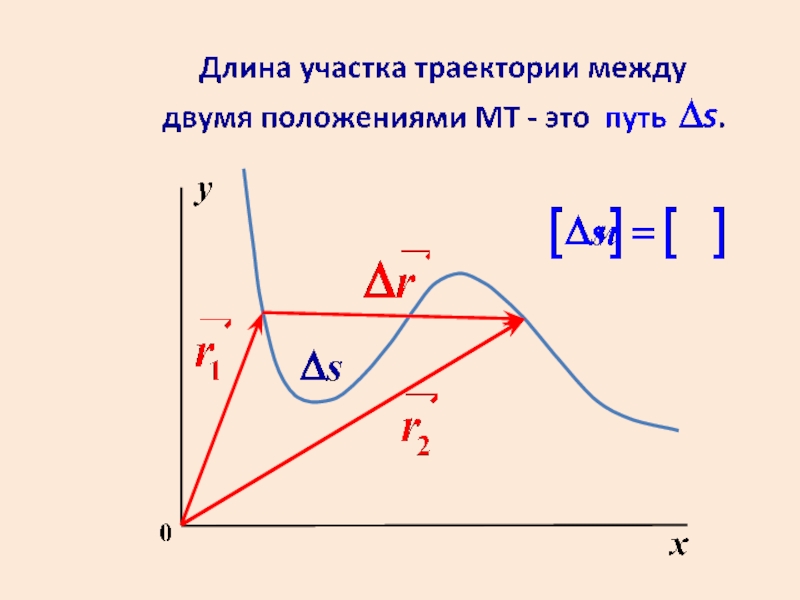
Слайд 31Путь и модуль вектора перемещения равны только в случае однонаправленного прямолинейного
движения. Во всех других случаях путь больше.
Обе величины равны также при бесконечно малом перемещении.
Слайд 32СКОРОСТЬ
Скорость – это величина, характеризующая быстроту изменения радиус-вектора материальной точки со
временем.
Слайд 33
Средний вектор скорости
равен отношению перемещения к промежутку времени, за который
оно произошло.
Слайд 34Средняя путевая скорость
(средний модуль скорости) равна отношению пути к промежутку времени,
за который этот путь пройден.
Слайд 36Мгновенная скорость – это скорость в данный момент времени. Ее находят
как предел средней скорости при Δt→0.
Слайд 37Мгновенная скорость равна производной радиус-вектора по времени.
Вектор мгновенной скорости направлен
по касательной к траектории.
Слайд 40
Путь, пройденный за время от t1 до t2:
На графике это площадь
под кривой v(t).
В случае v=const.:
В случае v=const.:
