- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кинематическое исследование механизмов и машин презентация
Содержание
- 1. Кинематическое исследование механизмов и машин
- 2. Функция положения механизма
- 3. Кинематические передаточные функции механизма –
- 4. Геометрические и кинематические характеристики механизма
- 5. Механизм с одной подвижностью
- 6. Схема механической системы Схема включает
- 7. Блок-схема рассмотренной механической системы
- 8. Функции положения в механизмах
- 9.
- 10. - кинематических диаграмм
- 11. 2 3 4
- 12. 2 3 4
- 13. s2b as2 s2 A B
- 14. Графо-аналитический метод (метод
- 15. e s1 f c C d
- 16. S1 s1 n2 e n6 n3
- 18. Задача о положениях звеньев механизма
- 20. Задача о первых кинематических
- 21. Задача о вторых передаточных функциях
- 22. Выполнив вычисления по приве-дённым выше зависимостям, пост-роим соответствующие диаграм-мы.
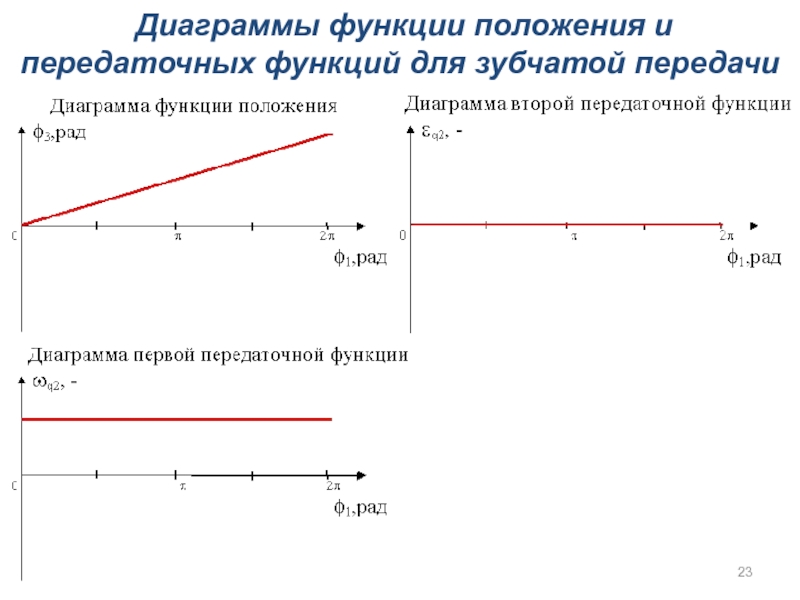
- 23. Диаграммы функции положения и передаточных функций для зубчатой передачи
- 24. Диаграммы функции положения
- 27. Экспериментальный метод кинематического исследования
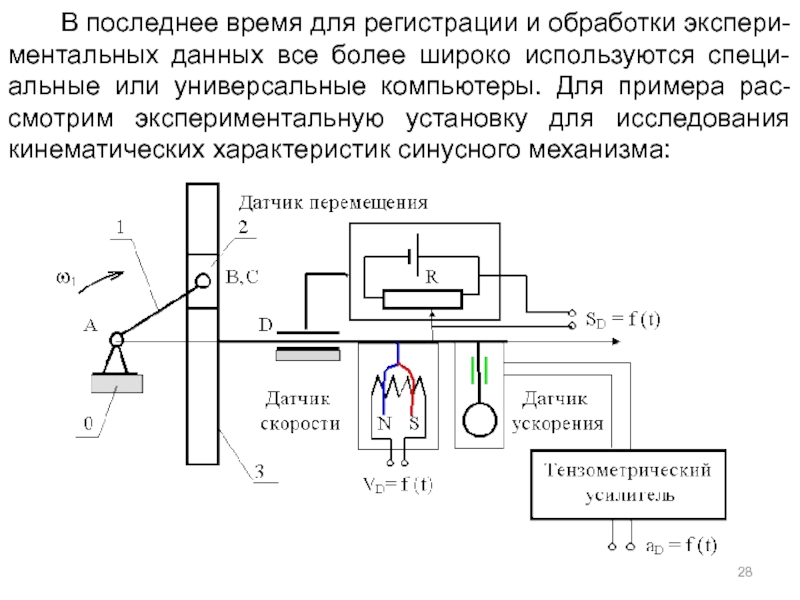
- 28. В последнее время
- 29. В этой экспериментальной установке:
- 30. для измерения ускорения выходного звена использу-ется
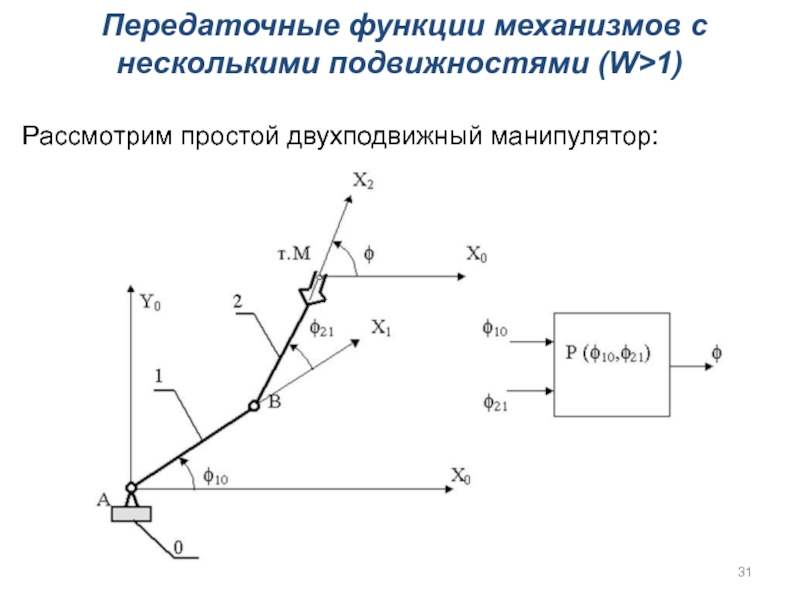
- 31. Передаточные функции механизмов с несколькими подвижностями (W>1) Рассмотрим простой двухподвижный манипулятор:
- 32. Функция положения для выходного звена
Слайд 2
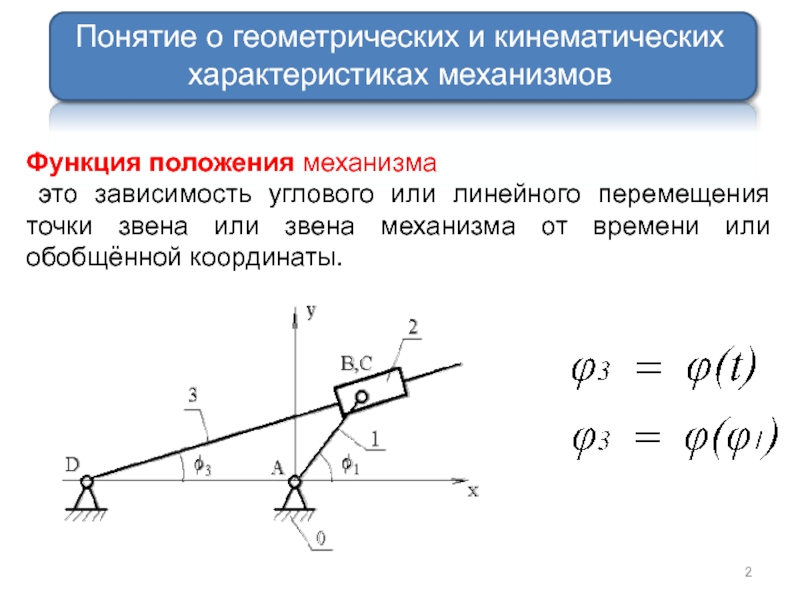
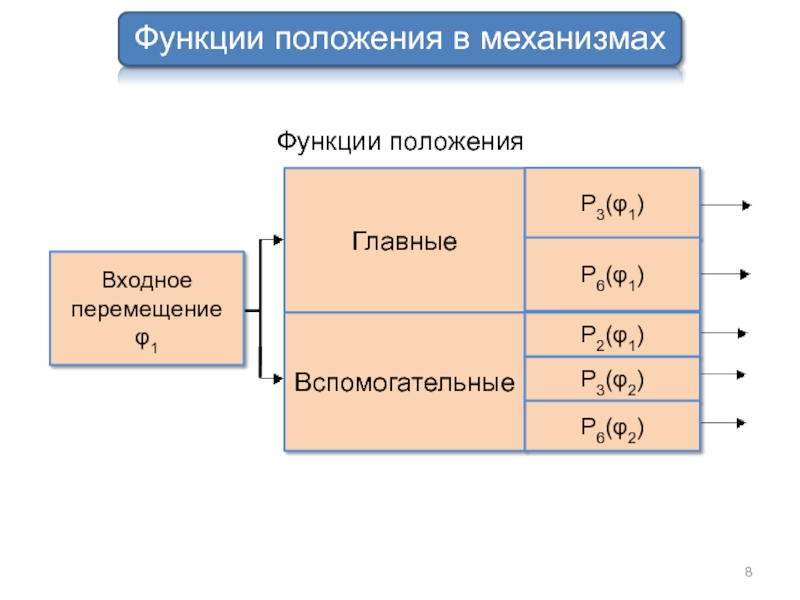
Функция положения механизма
это зависимость углового или линейного перемещения точки звена
Понятие о геометрических и кинематических
характеристиках механизмов
Слайд 3
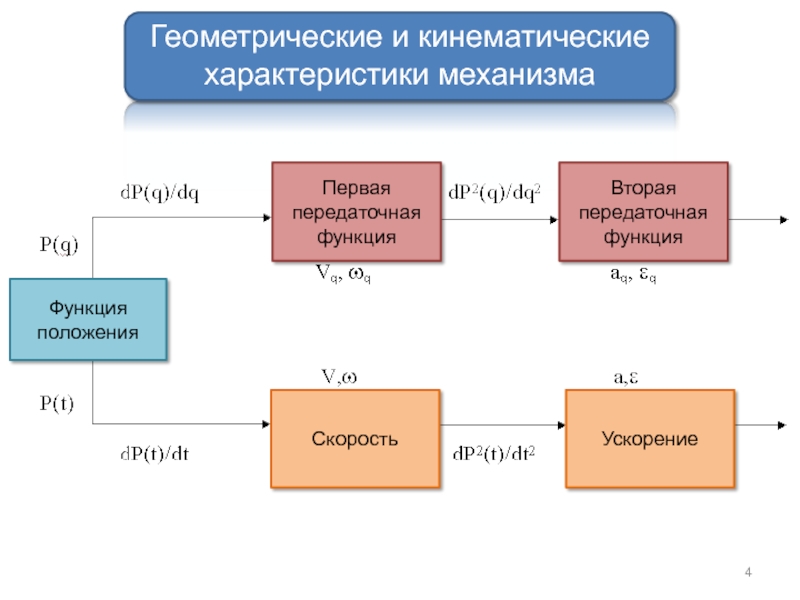
Кинематические передаточные функции механизма –
производные от функции положения по обобщенной коор-динате.
Первая производная называется первой передаточной функцией или аналогом скорости (обозначается ),
Вторая - второй передаточной функцией или аналогом ускорения (обозначается ).
Кинематические характеристики механизма –
производные от функции положения по времени.
Первая производная называется скоростью (обозначается ),
вторая - ускорением (обозначается ).
Слайд 5
Механизм с одной подвижностью имеет одно заданное входное движение
Передаточные функции тех движений, которые в данном случае используются как выходные, называются главными, остальные - вспомогательными.
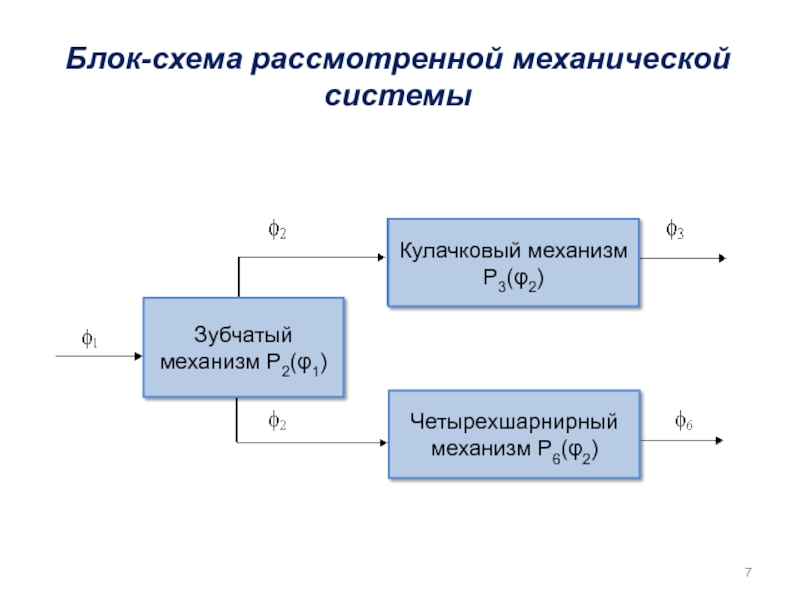
Рассмотрим схему механической системы образованной последовательно-параллельным соединением типовых механизмов.
Слайд 6
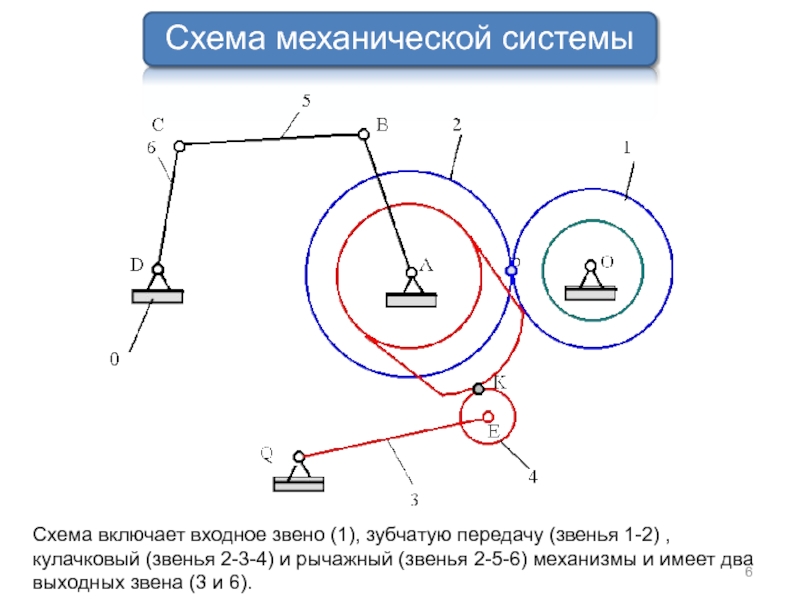
Схема механической системы
Схема включает входное звено (1), зубчатую передачу (звенья 1-2)
Слайд 9
Линейные скорости и ускорения
Угловые скорости и ускорения
Связь
Слайд 10
- кинематических диаграмм (графический),
- планов положений, скоростей и ускорений
- проекций векторного контура (аналитический),
- преобразования координат (аналитический),
- экспериментальный.
Методы кинематического
исследования механизмов
Слайд 112 3 4
C
4
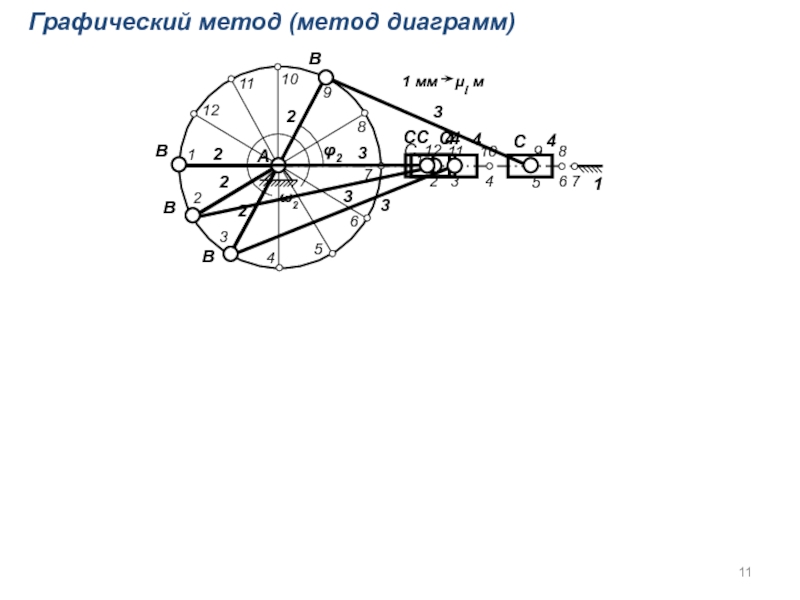
Графический метод (метод диаграмм)
1
2
3
5
6
7
8
9
10
11
12
A
ω2
φ2
5
8
12
10
C1
9
4
3
2
B
1 мм μl м
1
B
3
2
C
4
B
C
4
3
2
B
2
3
C
4
11
Слайд 122 3 4
4
Графический метод (метод диаграмм)
SC
VC
aC
l мм
1 2 3 4 5 6 7 8 9 10 11 12 1
1 мм μt с
1 мм μs м
1 мм μφ рад
t,φ2
0
1
2
3
5
6
7
8
9
10
11
12
A
ω2
φ2
5
8
12
10
C1
9
1 мм μl м
1
SC=SC(t)
VC=VC(t)
1 мм μv м/с
aC=aC(t)
1 мм μa м/с2
B
2
3
C
4
11
Слайд 13s2b
as2
s2
A
B
O1
O3
1
2
3
VBA
VBA
VB
VA
VB = VA + VBA
VA
VB
S2
a
b
AS2
S2B
=
PV
s2
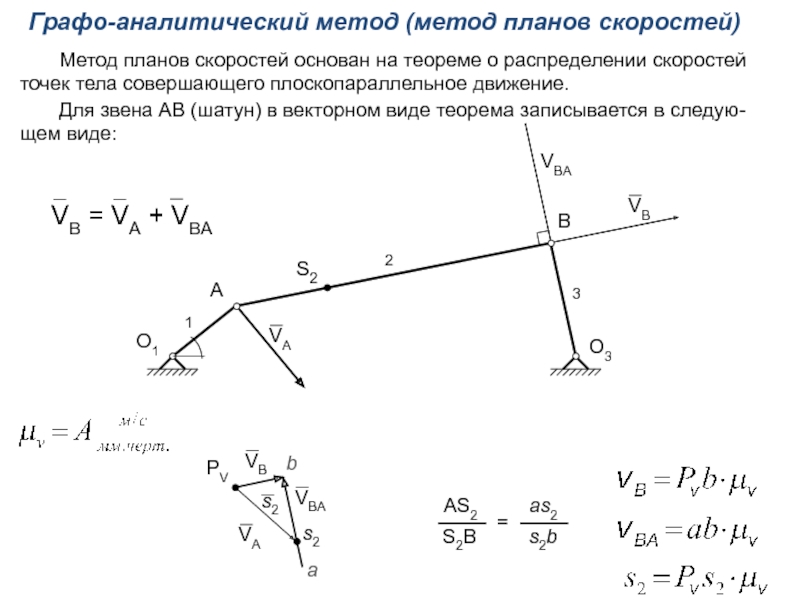
Графо-аналитический метод (метод планов скоростей)
Метод планов
Для звена АВ (шатун) в векторном виде теорема записывается в следую-щем виде:
Слайд 14
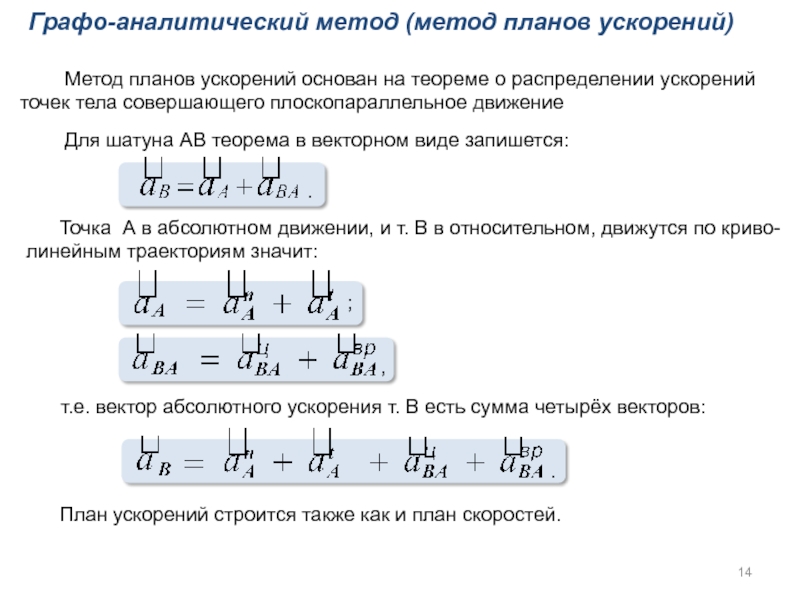
Графо-аналитический метод (метод планов ускорений)
Метод планов ускорений основан на теореме
Для шатуна АВ теорема в векторном виде запишется:
.
;
т.е. вектор абсолютного ускорения т. В есть сумма четырёх векторов:
,
Точка А в абсолютном движении, и т. В в относительном, движутся по криво-
линейным траекториям значит:
.
План ускорений строится также как и план скоростей.
Слайд 15e
s1
f
c
C
d
B
b
p
1
4
E
2
5
F
G
D
3
6
S1
S2
S3
g
7
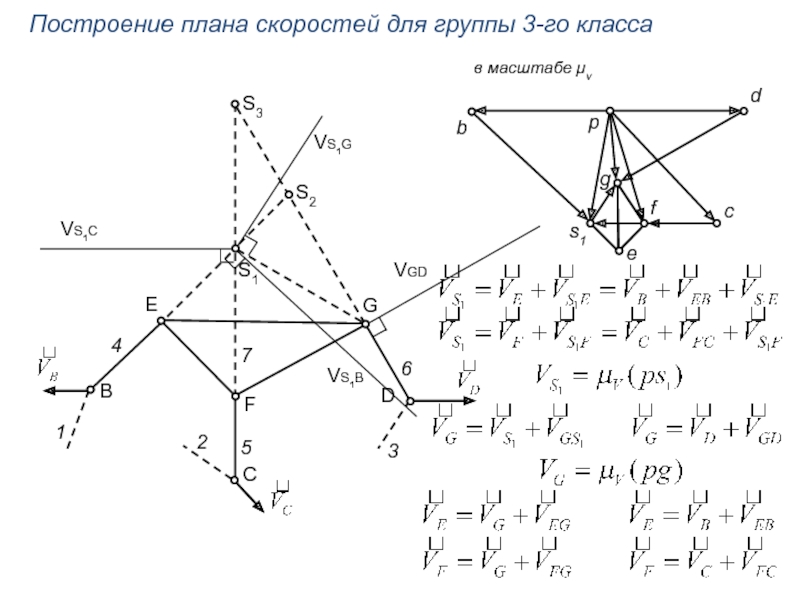
в масштабе μv
VS1B
VS1C
VS1G
VGD
Построение плана скоростей для группы 3-го класса
Слайд 16S1
s1
n2
e
n6
n3
F
d
b
C
B
1
4
E
2
5
G
D
3
6
S2
S3
7
в масштабе μa
c
n1
g
f
n5
n4
π
(1)
(3)
(2.1)
(2.2)
(2.3)
(2.4)
(4)
(6)
(5)
(8)
(7)
Слайд 17
Рассмотрим простейший кулисный механизм.
Тогда уравнение замкнутости векторного контура запи-шется:
Аналитический метод кинематического анализа.
Метод проекций векторного замкнутого контура.
Слайд 18
Задача о положениях звеньев механизма
Проецируем векторный
(1)
(2)
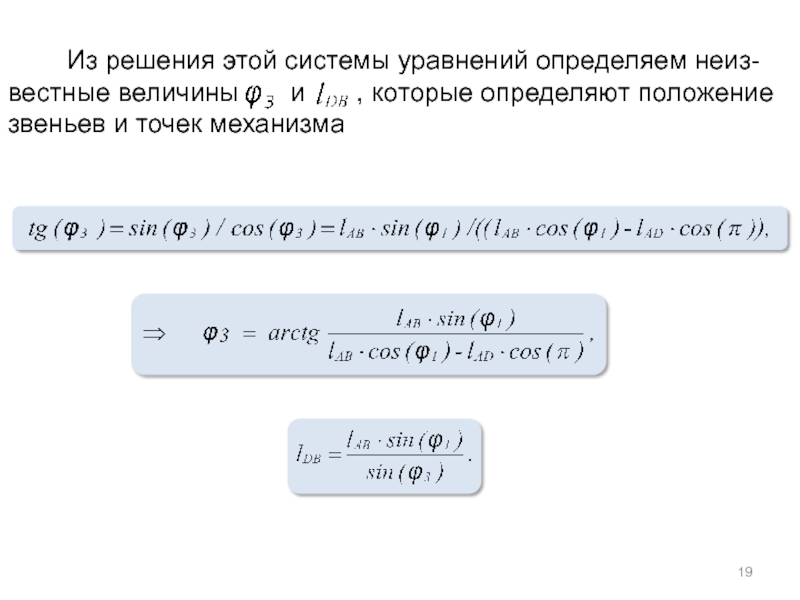
Слайд 19
Из решения этой системы уравнений определяем неиз-вестные
Слайд 20
Задача о первых кинематических передаточных функциях механизма
Продифференцируем уравнения
Из этой системы уравнений определяем первые переда-точные функции VqB и .
Слайд 21
Задача о вторых передаточных функциях механизма
Вторично продифференцируем уравнения проекций вектор-ного контура
Из этой системы уравнений определяем вторые переда-точные функции и .
Слайд 22Выполнив вычисления по приве-дённым выше зависимостям, пост-роим соответствующие диаграм-мы.
Слайд 24
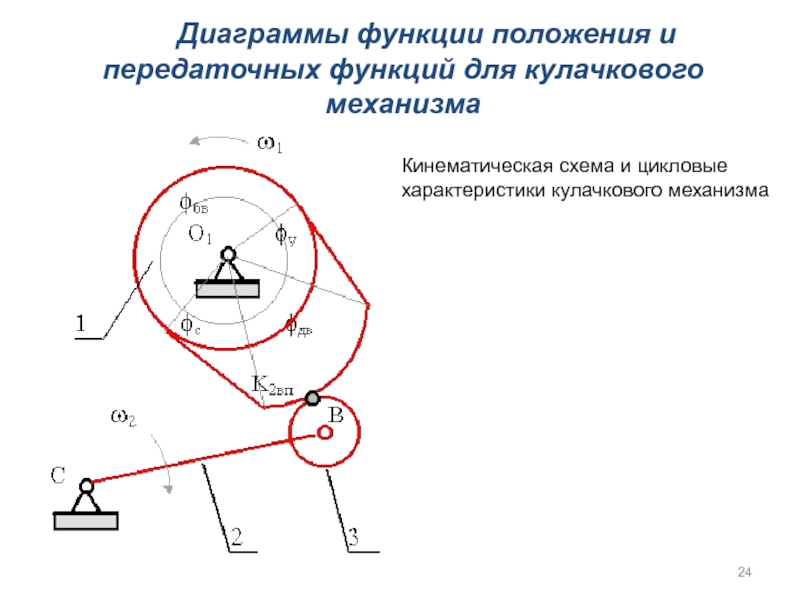
Диаграммы функции положения и передаточных функций для кулачкового
Кинематическая схема и цикловые
характеристики кулачкового механизма
Слайд 27Экспериментальный метод кинематического исследования
При экспериментальном исследовании кинематики
Слайд 28 В последнее время для регистрации и обработки
Слайд 29
В этой экспериментальной установке:
для измерения перемещения выходного звена исполь-зуется потенциометрический датчик
для измерения скорости выходного звена используется идукционный датчик скорости, в котором напряжение на кон-цах катушки движущейся в поле постоянного магнита про-порционально скорости катушки;
Слайд 30
для измерения ускорения выходного звена использу-ется тензометрический акселерометр. Он состоит из
Слайд 31 Передаточные функции механизмов с несколькими подвижностями (W>1)
Рассмотрим простой двухподвижный
Слайд 32
Функция положения для выходного звена этого механизма является функцией двух переменных
и
где и - частные производные по обобщён-ным координатам.
Конец ЛТММ3.