крутящих моментов и поперечных сил через функцию прогибов пластины. Уравнения равновесия элемента пластинки. Уравнение Софи-Жермен–Лагранжа. Формулировка граничных условий для основных случаев закрепления краев пластинки.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Изгиб пластин презентация
Содержание
- 1. Изгиб пластин
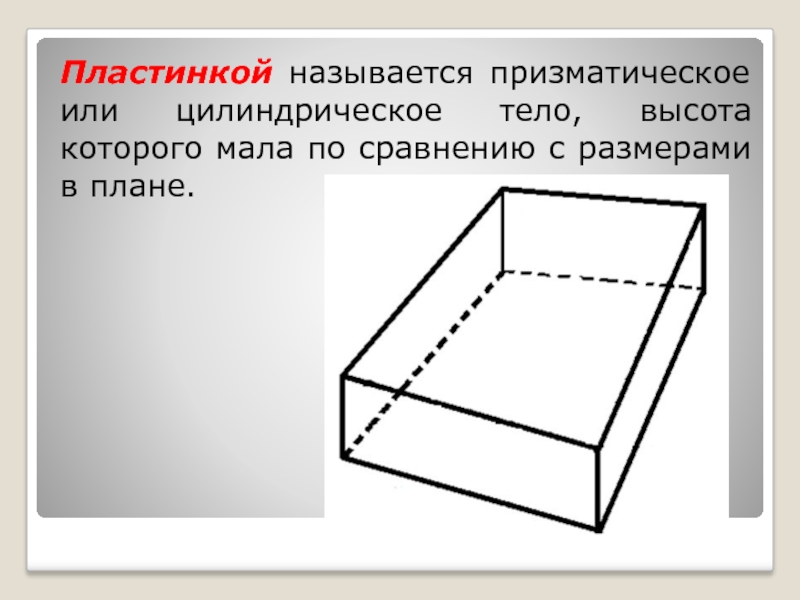
- 2. Пластинкой называется призматическое или цилиндрическое тело, высота которого мала по сравнению с размерами в плане.
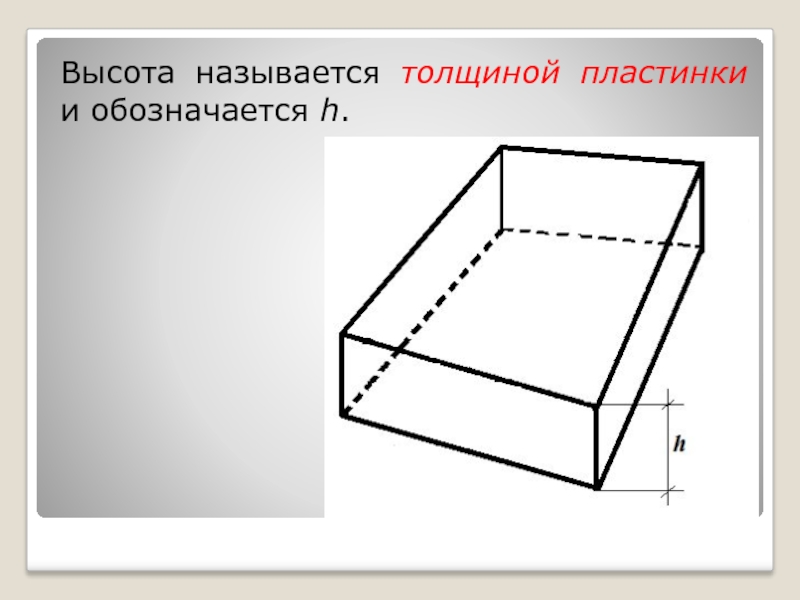
- 3. Высота называется толщиной пластинки и обозначается h.
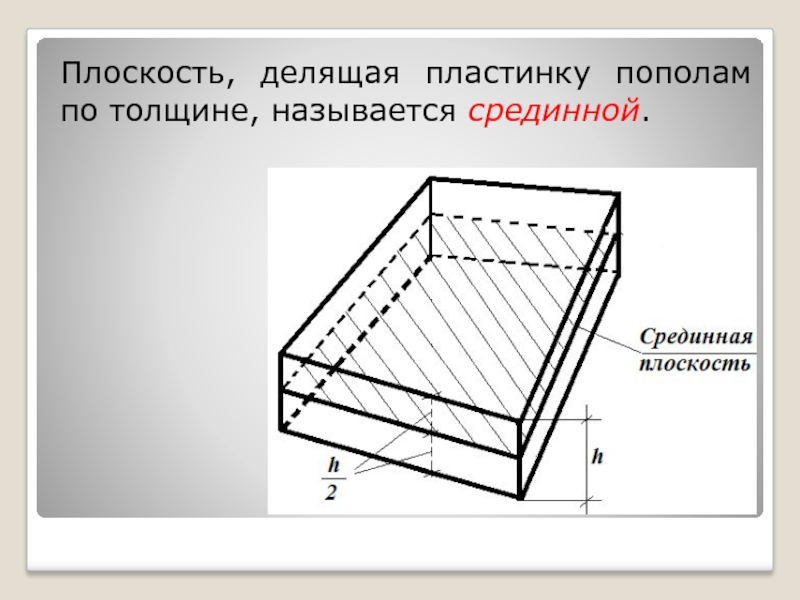
- 4. Плоскость, делящая пластинку пополам по толщине, называется срединной.
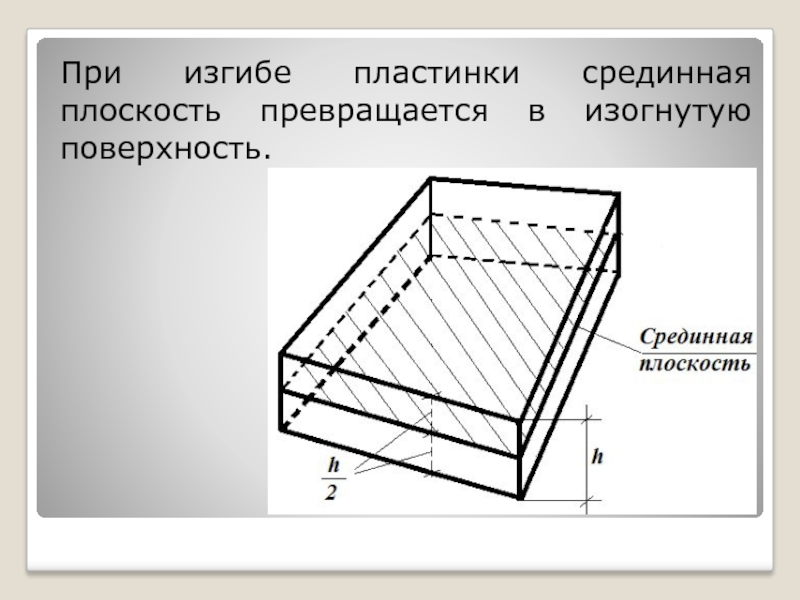
- 5. При изгибе пластинки срединная плоскость превращается в изогнутую поверхность.
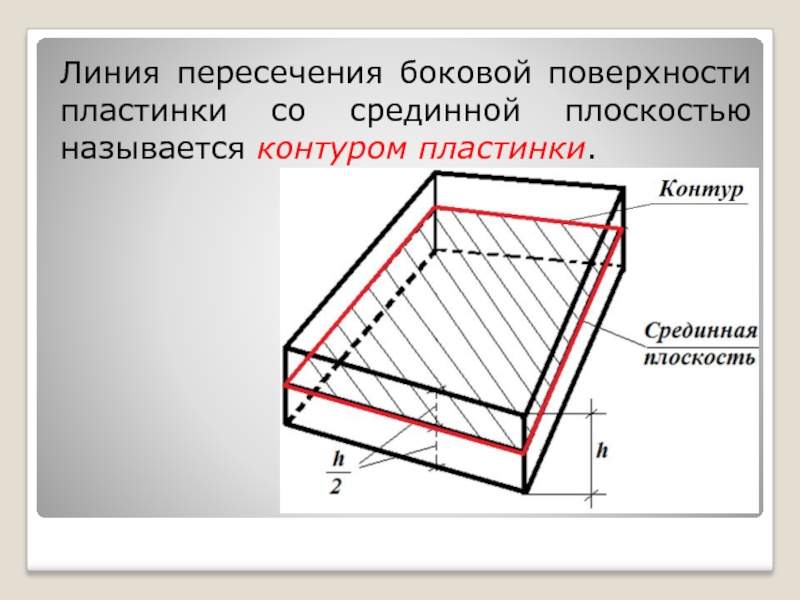
- 6. Линия пересечения боковой поверхности пластинки со срединной плоскостью называется контуром пластинки.
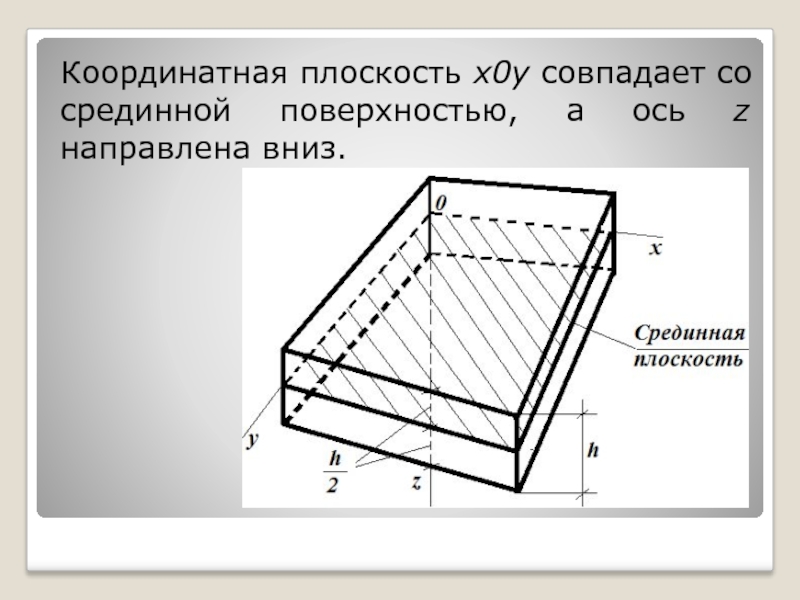
- 7. Координатная плоскость x0y совпадает со срединной поверхностью, а ось z направлена вниз.
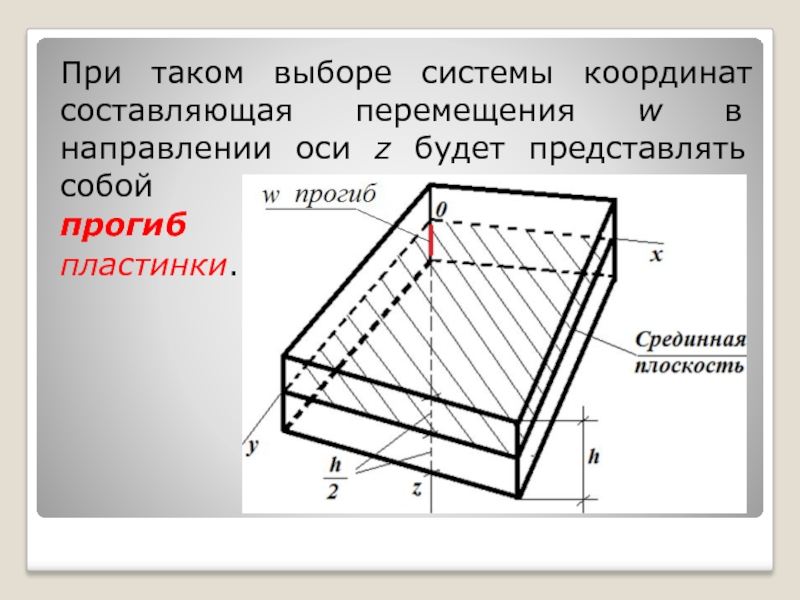
- 8. При таком выборе системы координат составляющая перемещения
- 9. Положение начала координат в срединной плоскости будем
- 10. Пластинки находят широкое применение в строительстве в
- 11. Тонкими называются пластинки, имеющие отношение характерного размера в плане к толщине примерно в пределах
- 12. Толстыми называются пластинки, имеющие отношение характерного размера в плане к толщине примерно в пределах
- 13. Мембранами называются пластинки, имеющие отношение характерного размеру в плане к толщине примерно в пределах
- 14. Тонкие пластинки обычно рассчитывают по приближенной теории
- 15. 1. Гипотеза прямых нормалей: любой прямолинейный элемент,
- 16. Любой прямолинейный элемент, нормальный к срединной плоскости,
- 17. Гипотеза о сохранении длины прямоугольного элемента предполагает,
- 18. 2. Гипотеза о недеформируемости срединной плоскости: в
- 19. 3. Гипотеза об отсутствии давления между слоями
- 20. Перемещения и деформации в пластинке Изучение изгиба
- 21. Следуя первой гипотезе и подставляя условие (2)
- 22. Это означает, что все точки
- 23. Рассматривая условия для сдвигов (1), из геометрических
- 24. отсюда находим производные составляющих перемещения u и
- 25. Для вычисления функций и
- 26. Таким образом, составляющие перемещения точек пластинки в
- 27. Составляющие деформации пластинки, отличные от нуля, находим
- 28. Здесь составляющие деформации, так же как и
- 29. Напряжения в пластинке Для вычисления нормальных напряжений
- 30. Из (8) с учетом зависимостей (7) находим
- 31. Четвертая формула закона Гука после подстановки угловой
- 32. Касательные напряжения в двух других плоскостях, согласно
- 34. Действительно, рассмотрим дифференциальные уравнения равновесия. Пренебрегая объемными
- 35. Подставим сюда напряжения из формул (9) и
- 36. или Интегрируя по z, находим
- 37. Для определения произвольной функции
- 38. Отсюда искомая функция
- 39. Решая таким же путем второе уравнение равновесия,
- 40. Итак, согласно формулам (9), (10), (14) и
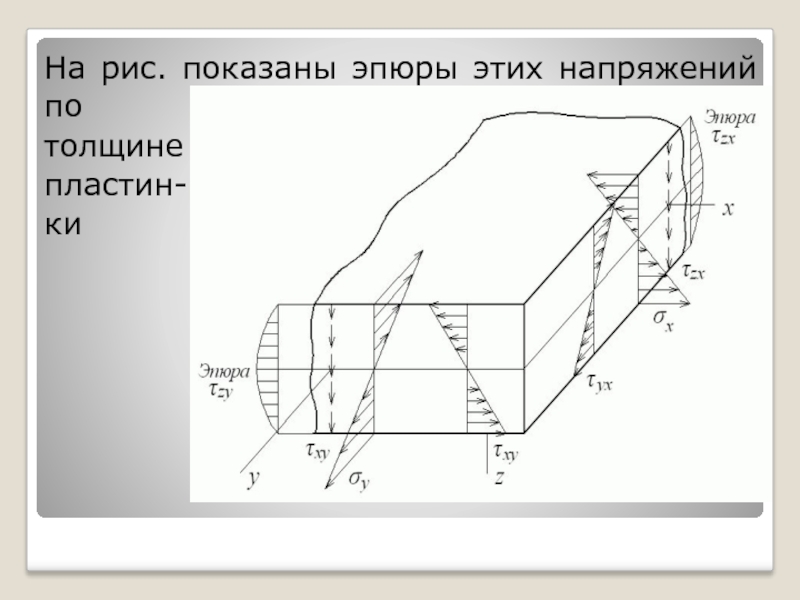
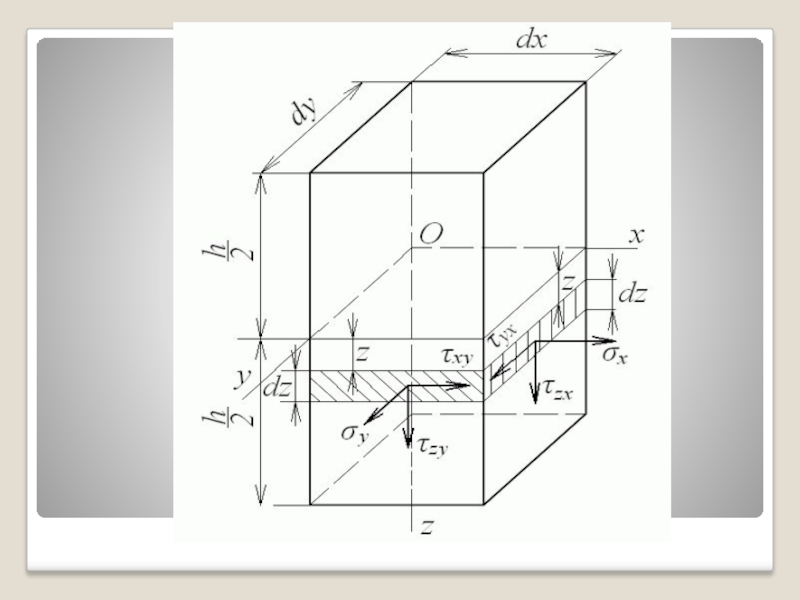
- 42. На рис. показаны эпюры этих напряжений по толщине пластин- ки
- 43. Напряжения , и и
- 44. Усилия в пластинке Рассмотрим, какие усилия соответствуют
- 46. Рассмотрим вначале площадку с нормалью, параллельной оси
- 47. Обозначим через нормальную силу, приходящуюся
- 48. Под действием поперечной нагрузки в сечениях пластинки,
- 49. Дифференциальное уравнение изогнутой срединной поверхности пластинки
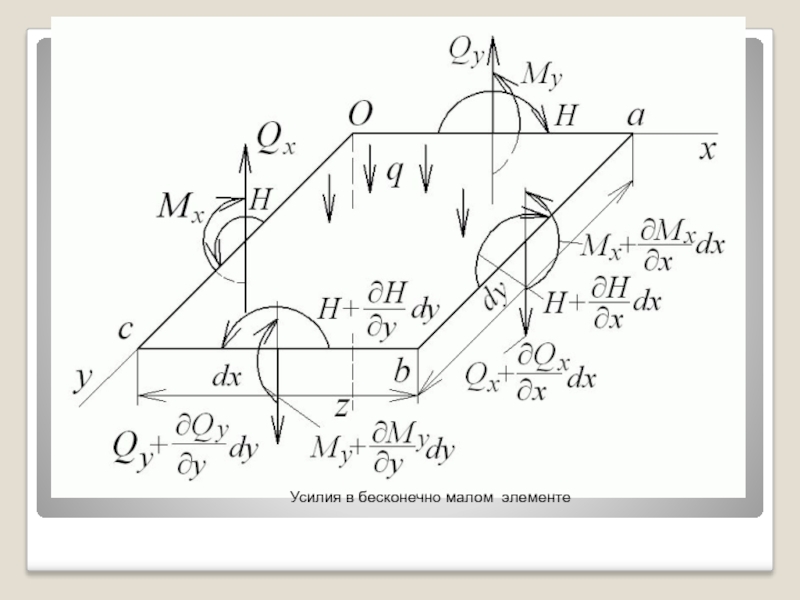
- 50. Усилия в бесконечно малом элементе
- 51. На грани Ос действует поперечная сила
- 52. Для того чтобы рассматриваемый элемент срединной плоскости
- 53. Спроецируем все силы, изображенные на рис. На
- 54. Уравнение моментов всех сил относительно оси y
- 55. Аналогично, из уравнения моментов всех сил относительно
- 56. Подставим в это уравнение выражения моментов
- 57. В сокращенной форме записи
- 58. Получили основное уравнение
- 59. Условия на контуре пластинки В зависимости от
- 60. Условия на контуре пластинки Условия, при
- 61. Условия на контуре пластинки Условия, при которых
- 62. Условия на контуре пластинки Если же заданы
- 63. Сформулируем граничные условия для различных случаев закрепления краев прямоугольной пластинки представ- ленной на рис.
- 64. Защемленный край OA. В защемлении отсутствуют прогибы
- 65. Шарнирно опертые края ОС и АВ. На
- 66. Однако при
- 67. Свободный край СВ. Здесь должны обращаться в
- 68. Свободный край СВ. Здесь должны обращаться в
- 69. На свободной грани CB ,т.е. при y=b,
Пластинкой называется призматическое или цилиндрическое тело, высота которого мала по сравнению с размерами в плане.
Слайд 1Изгиб пластин
Классификация пластин. Основные понятия и гипотезы. Выражение деформаций, напряжений, изгибающих,
Слайд 2Пластинкой называется призматическое или цилиндрическое тело, высота которого мала по сравнению
с размерами в плане.
Слайд 6Линия пересечения боковой поверхности пластинки со срединной плоскостью называется контуром пластинки.
Слайд 8При таком выборе системы координат составляющая перемещения w в направлении оси
z будет представлять собой
прогиб
пластинки.
прогиб
пластинки.
Слайд 9Положение начала координат в срединной плоскости будем выбирать в каждом рассматриваемом
случае в зависимости от очертания контура пластинки и характера закрепления её краёв.
Слайд 10 Пластинки находят широкое применение в строительстве в виде настилов и панелей,
железобетонных плит для покрытия производственных зданий, плит фундаментов массивных зданий и т. д. Расчетной схемой плит, применяемых в строительных конструкциях, является тонкая пластинка.
Слайд 11Тонкими называются пластинки, имеющие отношение характерного размера в плане к толщине
примерно в пределах
Слайд 12Толстыми называются пластинки, имеющие отношение характерного размера в плане к толщине
примерно в пределах
Слайд 13Мембранами называются пластинки, имеющие отношение характерного размеру в плане к толщине
примерно в пределах
Слайд 14 Тонкие пластинки обычно рассчитывают по приближенной теории — технической теории изгиба
пластинок, которая основана на следующих гипотезах, предложенных немецким физиком Г. Кирхгофом.
Слайд 151. Гипотеза прямых нормалей: любой прямолинейный элемент, нормальный к срединной плоскости,
остается прямолинейным и нормальным к срединной поверхности после деформирования пластинки, и длина его не изменяется. Эта гипотеза аналогична гипотезе плоских сечений в теории изгиба балок.
Слайд 16Любой прямолинейный элемент, нормальный к срединной плоскости, направлен вдоль оси z,
и, следовательно, первая часть гипотезы предполагает, что прямые углы между этим элементом и осями x, y остаются прямыми, т.е. сдвиги в указанных плоскостях отсутствуют
(1)
(1)
Слайд 17Гипотеза о сохранении длины прямоугольного элемента предполагает, что линейная деформация в
направлении оси z (по толщине пластинки) отсутствует:
(2)
(2)
Слайд 182. Гипотеза о недеформируемости срединной плоскости: в срединной плоскости отсутствуют деформации
растяжения, сжатия и сдвига, т. е. она является нейтральной и ее перемещения
(3)
(3)
Слайд 193. Гипотеза об отсутствии давления между слоями пластинки, параллельными срединной плоскости.
Гипотеза позволяет пренебрегать напряжением ввиду малости по сравнению с напряжениями
и . Аналогичная гипотеза принималась в теории изгиба балок.
и . Аналогичная гипотеза принималась в теории изгиба балок.
Слайд 20Перемещения и деформации в пластинке
Изучение изгиба пластинки начнем с определения перемещений
и деформаций. Исследуем пластинку, несущую поперечную нагрузку, т. е. нагрузку, нормальную к срединной плоскости пластинки. Под действием этой нагрузки пластинка получит перемещения. Для их определения обратимся к принятым гипотезам.
Слайд 21Следуя первой гипотезе и подставляя условие (2) в геометрические соотношения Коши,
получаем
откуда следует, что прогибы пластинки w
не зависят от координаты z, т. е
откуда следует, что прогибы пластинки w
не зависят от координаты z, т. е
Слайд 22
Это означает, что все точки пластинки, лежащие на одной вертикали, получают
одинаковые перемещения w. Следовательно, достаточно определить прогибы срединной плоскости пластинки, чтобы знать вертикальные перемещения всех ее точек.
Слайд 23Рассматривая условия для сдвигов (1), из геометрических соотношений Коши получаем
(4)
отсюда находим производные составляющих перемещения u и v:
отсюда находим производные составляющих перемещения u и v:
;
;
Слайд 24отсюда находим производные составляющих перемещения u и :
Интегрируя эти выражения
по z, получаем
(5)
(5)
Слайд 25Для вычисления функций
и , появившихся при интегрировании
уравнений в частных производных, воспользуемся гипотезой о недеформируемости срединной плоскости. Подставляя условия (3) в формулы (5) при z=0, получаем:
(6)
(6)
Слайд 26 Таким образом, составляющие перемещения точек пластинки в направлениях осей x и
y выражены через функцию прогибов срединной плоскости пластинки.
Слайд 27 Составляющие деформации пластинки, отличные от нуля, находим с помощью формул Коши,
подставляя в них значения составляющих перемещения (6).
(7)
(7)
Слайд 28 Здесь составляющие деформации, так же как и составляющие перемещения в соотношениях
(6), выражены через одну функцию прогибов срединной плоскости пластинки.
Слайд 29Напряжения в пластинке
Для вычисления нормальных напряжений
и воспользуемся двумя первыми
формулами закона Гука и на основании третьей гипотезы отбросим напряжение . Тогда получим:
(8)
(8)
Слайд 31Четвертая формула закона Гука после подстановки угловой деформации из формул (7)
принимает следующий вид:
(10)
(10)
Слайд 32Касательные напряжения в двух других плоскостях, согласно равенствам (1), обращаются в
нуль:
(11)
(11)
Слайд 33
(11)
Однако такой результат получен только вследствие принятых ранее гипотез. В действительности эти касательные напряжения не равны нулю, поскольку это противоречит условиям равновесия.
Слайд 34 Действительно, рассмотрим дифференциальные уравнения равновесия. Пренебрегая объемными силами, из первого уравнения
находим
(12)
(12)
Слайд 37
Для определения произвольной функции f3(x,y) имеем следующие граничные условия: на верхней
и нижней поверхностях пластинки нет касательных нагрузок, т. е. при . Подставляя эти условия в формулу (13), получаем
Слайд 40Итак, согласно формулам (9), (10), (14) и (15), в сечениях пластинки,
перпендикулярных ее срединной плоскости, возникают следующие напряжения:
Слайд 43 Напряжения , и и распределяются
по линейному закону, обращаясь в нуль в точках срединной плоскости;
напряжения и распределяются по параболе, достигая в точках срединной плоскости максимального значения. Так же распределяются касательные напряжения и при поперечном изгибе балок прямоугольного сечения.
В формулах (16) все напряжения выражены через одну функцию двух переменных w(x,y), следовательно, функция прогибов играет здесь ту же роль, что и функция напряжений в плоской задаче.
напряжения и распределяются по параболе, достигая в точках срединной плоскости максимального значения. Так же распределяются касательные напряжения и при поперечном изгибе балок прямоугольного сечения.
В формулах (16) все напряжения выражены через одну функцию двух переменных w(x,y), следовательно, функция прогибов играет здесь ту же роль, что и функция напряжений в плоской задаче.
Слайд 44Усилия в пластинке
Рассмотрим, какие усилия соответствуют напряжениям (16) в сечениях пластинки,
нормальных к ее срединной плоскости. На рис. изображен бесконечно малый элемент пластинки, вырезанный такими сечениями.
Слайд 46 Рассмотрим вначале площадку с нормалью, параллельной оси x. По ней действуют
составляющие напряжений
, и . На рисунке показаны положительные напряжения: нормальное напряжение направлено по внешней нормали к сечению, а касательные — в направлении соответствующих положительных координатных осей, так как внешняя нормаль к сечению совпадает с положительным направлением оси x.
, и . На рисунке показаны положительные напряжения: нормальное напряжение направлено по внешней нормали к сечению, а касательные — в направлении соответствующих положительных координатных осей, так как внешняя нормаль к сечению совпадает с положительным направлением оси x.
Слайд 47 Обозначим через нормальную силу, приходящуюся на единицу ширины рассматриваемого
сечения. Она равна проекции на ось x равнодействующей внутренних сил в сечении с нормалью, параллельной оси x. На эту ось проецируется только нормальное напряжение . Соответствующая ему внутренняя сила на бесконечно малой площадке равна , а на единицу ширины сечения приходится сила . Суммируя эти элементарные силы по толщине пластинки, получаем выражение нормальной силы
Слайд 48 Под действием поперечной нагрузки в сечениях пластинки, перпендикулярных ее срединной плоскости,
возникают следующие усилия:
Изгибающие моменты:
Крутящий момент:
Поперечные силы:
Изгибающие моменты:
Крутящий момент:
Поперечные силы:
Слайд 49 Дифференциальное уравнение изогнутой срединной поверхности пластинки
Напряжения и усилия в пластинке выражены
через прогибы ее срединной плоскости. Следовательно, для определения напряжений и усилий необходимо знать функцию прогибов w(x,y).
Вырежем из срединной плоскости пластинки бесконечно малый элемент 0cba размерами dx, dy и покажем приложенные к нему усилия
Вырежем из срединной плоскости пластинки бесконечно малый элемент 0cba размерами dx, dy и покажем приложенные к нему усилия
Слайд 51 На грани Ос действует поперечная сила . На грани аb,
отстоящей от грани Ос на бесконечно малом расстоянии dx, поперечная сила получит бесконечно малое приращение и равна
Аналогично, на гранях оa и bc действуют соответственно поперечные силы и .
Нормально к срединной плоскости действует поверхностная нагрузка интенсивность q.
Аналогично, на гранях оa и bc действуют соответственно поперечные силы и .
Нормально к срединной плоскости действует поверхностная нагрузка интенсивность q.
Слайд 52 Для того чтобы рассматриваемый элемент срединной плоскости находился в равновесии, должны
удовлетворяться шесть условий равновесия: 3 уравнения проекций сил на координатные оси и 3 уравнения моментов относительно этих осей. При этом все усилия следует умножать на длину грани, по которой они действуют.
Слайд 55 Аналогично, из уравнения моментов всех сил относительно оси х следует
(3)
Исключим их уравнений (1)-(3) поперечные силы. В результате получим
Исключим их уравнений (1)-(3) поперечные силы. В результате получим
Слайд 58
Получили основное уравнение изгиба пластинки, обычно называемое уравнением Софи Жермен-Лагранжа. При
его интегрировании появятся произвольные постоянные, которые должны быть определены их условий на контуре пластинки, зависящих от характера закрепления её краёв.
Слайд 59Условия на контуре пластинки
В зависимости от характера закрепления краев на контуре
пластинки могут быть заданы прогибы и углы поворота срединной плоскости, изгибающие и крутящие моменты, поперечные силы.
Слайд 60Условия на контуре пластинки
Условия, при которых на контуре задаются перемещения,
т. е. прогибы или углы; поворота срединной плоскости, называются геометрическими.
Слайд 61Условия на контуре пластинки
Условия, при которых на контуре задаются усилия, т.
е. изгибающие или крутящие моменты и поперечные силы, называются статическими.
Слайд 62Условия на контуре пластинки
Если же заданы одновременно и перемещения, и усилия,
то условия называются смешанными. На каждом крае следует задать два граничных условия.
Слайд 63 Сформулируем граничные условия для различных случаев закрепления краев прямоугольной пластинки представ-
ленной
на
рис.
Слайд 64 Защемленный край OA. В защемлении отсутствуют прогибы и невозможен поворот краевого
сечения относительно оси x. В связи с этим имеем следующие условия:
при
при
Слайд 65 Шарнирно опертые края ОС и АВ. На них равны нулю прогибы
и изгибающие моменты, т.е. и . Выражая изгибающий момент через прогибы Выражая изгибаю-
щий момент через
прогибы пластинки,
последнее условие можно представить так:
щий момент через
прогибы пластинки,
последнее условие можно представить так:
Слайд 66 Однако при и
вторая производная .
Поэтому граничные
условия на шарнирно опертых краях и принимают вид:
при и
,
Поэтому граничные
условия на шарнирно опертых краях и принимают вид:
при и
,
Слайд 67 Свободный край СВ. Здесь должны обращаться в нуль изгибающий момент
, поперечная сила и крутящий момент , т.е. вместо необходимых двух условий появляются три.
Слайд 68 Свободный край СВ. Здесь должны обращаться в нуль изгибающий момент
, поперечная сила и крутящий момент , т.е. вместо необходимых двух условий появляются три. Такое противоречие связано с тем, что задача решается приближенно и поэтому всем граничным условиям точно удовлетворить нельзя. Однако противоречие можно устранить, объединив два последних условия.
