- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование динамической системы по временной реализации презентация
Содержание
- 1. Исследование динамической системы по временной реализации
- 2. Пусть мы имеем записанную реализацию x =
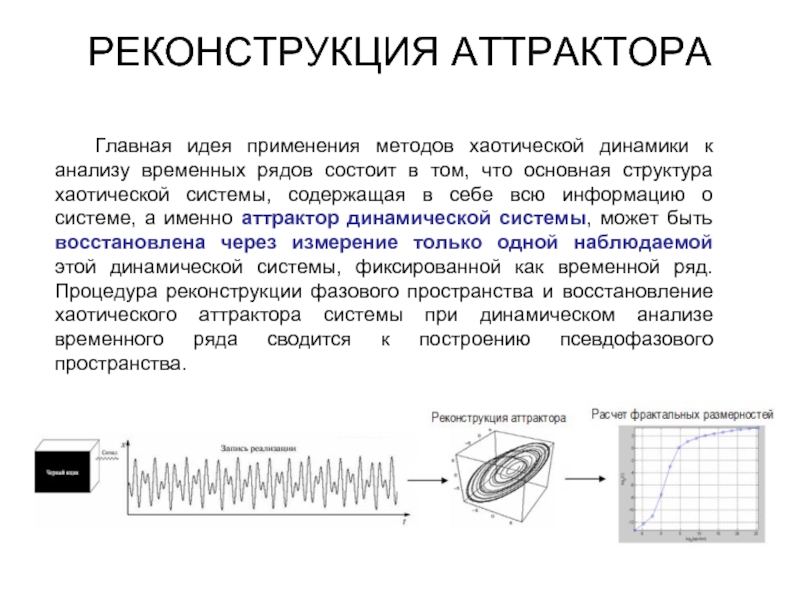
- 3. РЕКОНСТРУКЦИЯ АТТРАКТОРА Главная идея применения методов хаотической
- 4. РЕКОНСТРУКЦИЯ АТТРАКТОРА Теорема Уитни-Такенса.
- 5. РЕКОНСТРУКЦИЯ АТТРАКТОРА АТТРАКТОР ЧУА АТТРАКТОР ЛОРЕНЦА
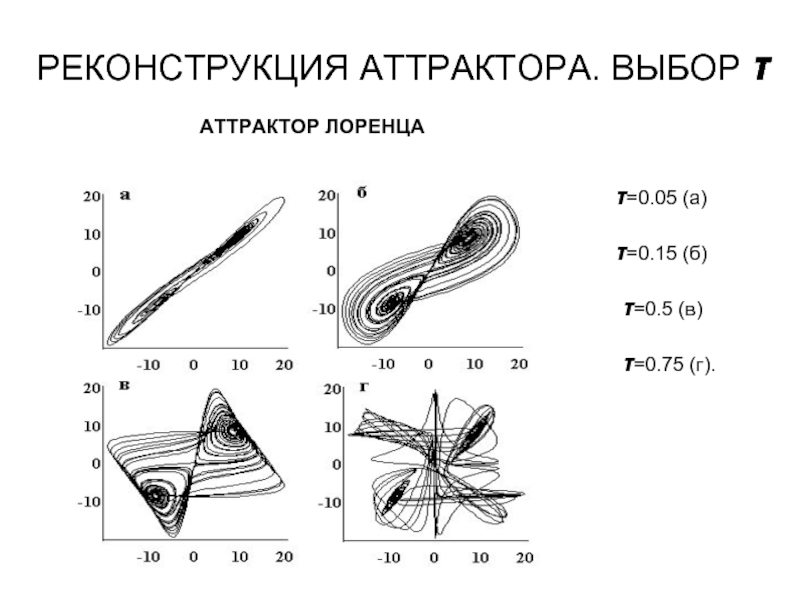
- 6. РЕКОНСТРУКЦИЯ АТТРАКТОРА. ВЫБОР τ
- 7. РЕКОНСТРУКЦИЯ АТТРАКТОРА. ВЫБОР τ АТТРАКТОР ЛОРЕНЦА
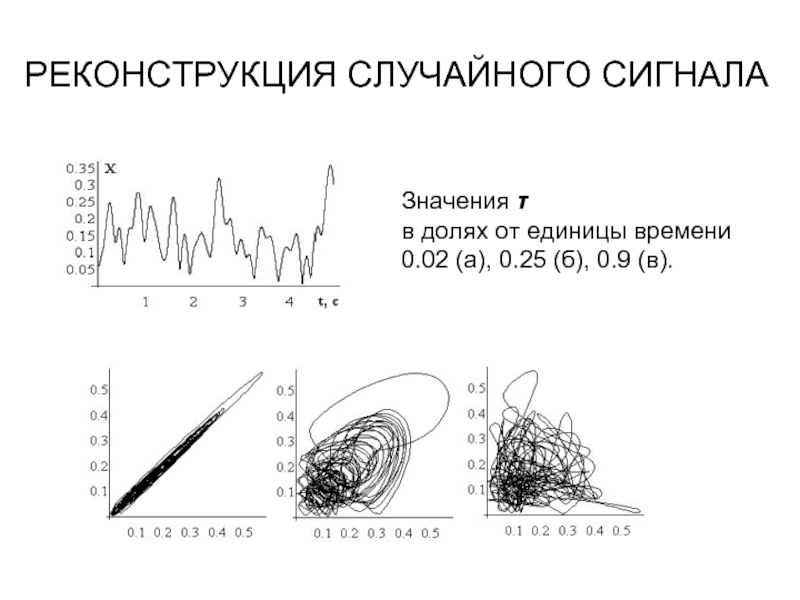
- 8. РЕКОНСТРУКЦИЯ СЛУЧАЙНОГО СИГНАЛА Значения τ
- 9. РАЗМЕРНОСТЬ ВЛОЖЕНИЯ Размерность вложения m –
- 10. ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ
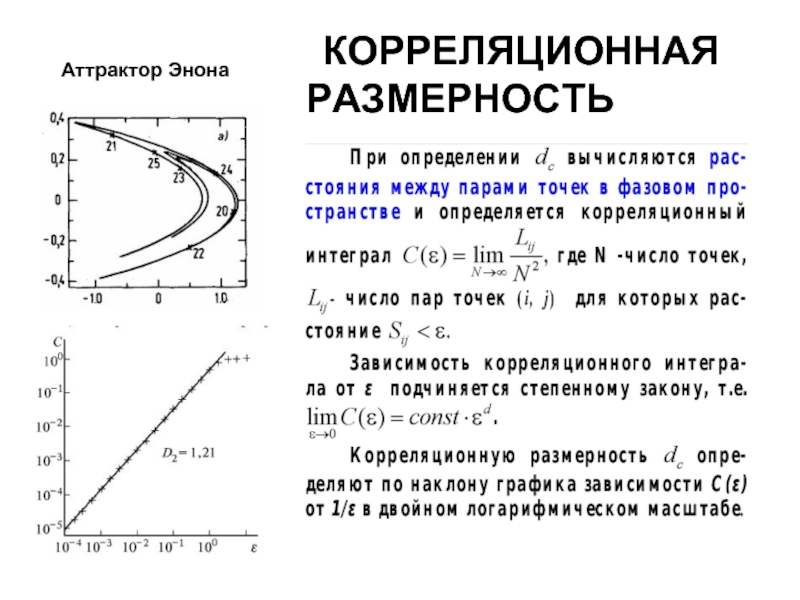
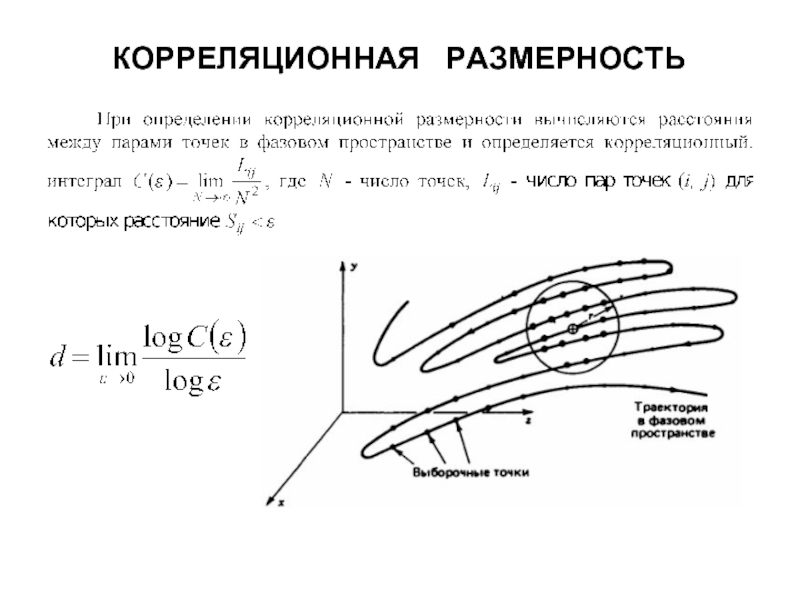
- 12. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ
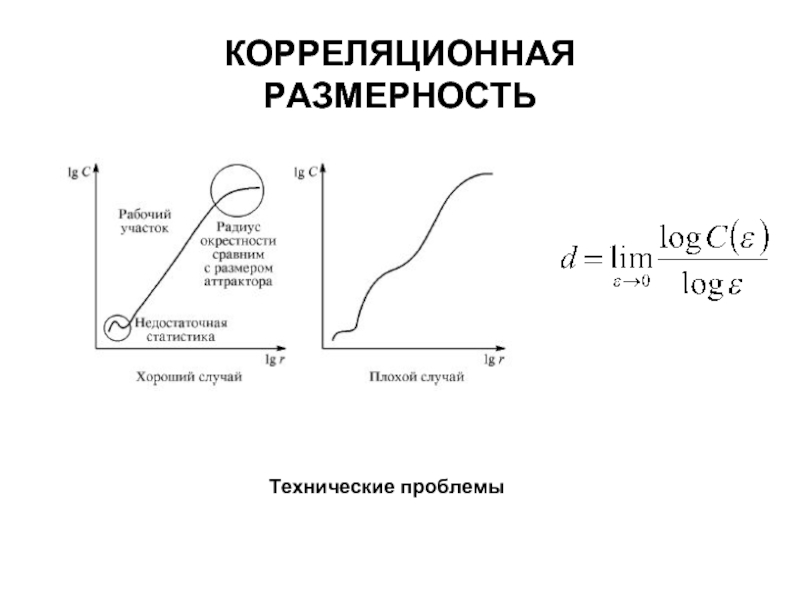
- 13. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ Технические проблемы
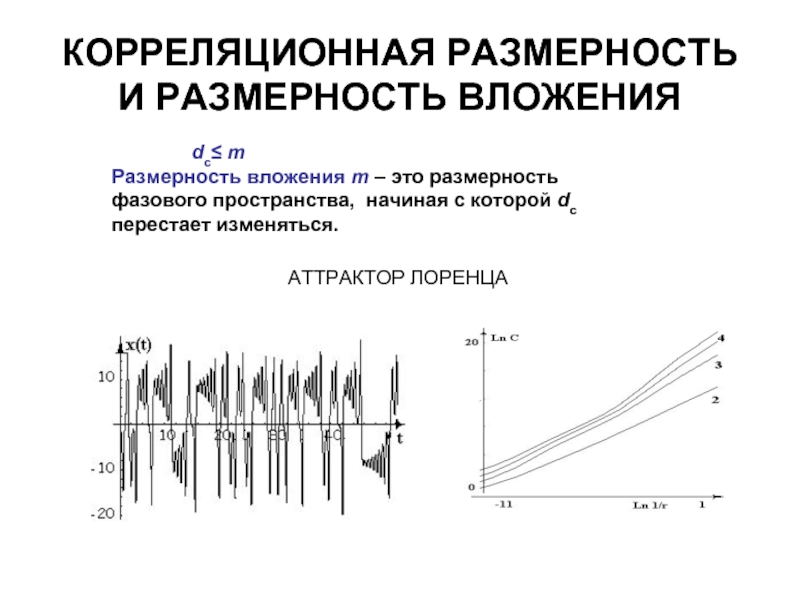
- 14. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ dc≤ m
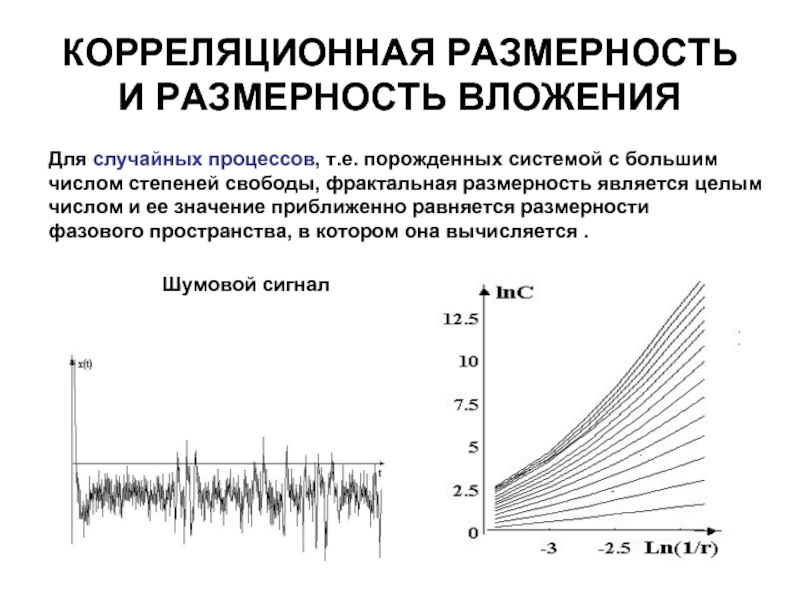
- 15. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ Для случайных
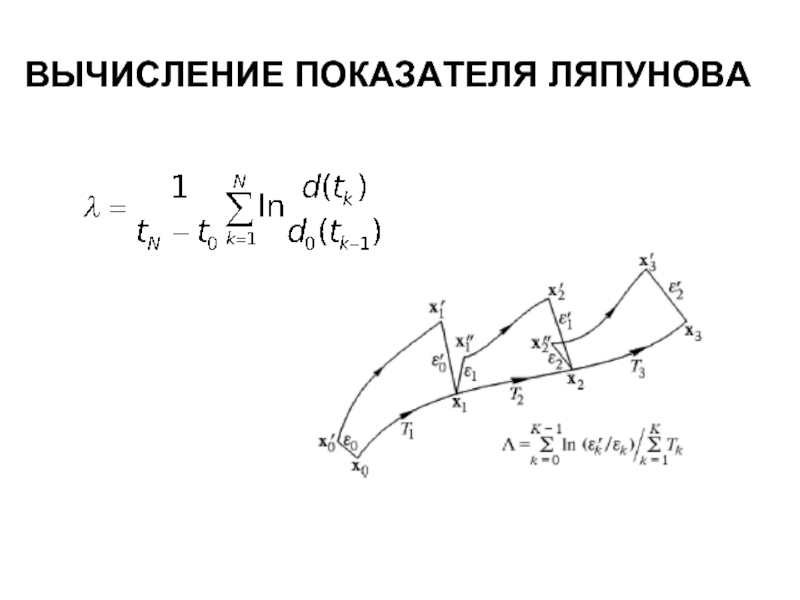
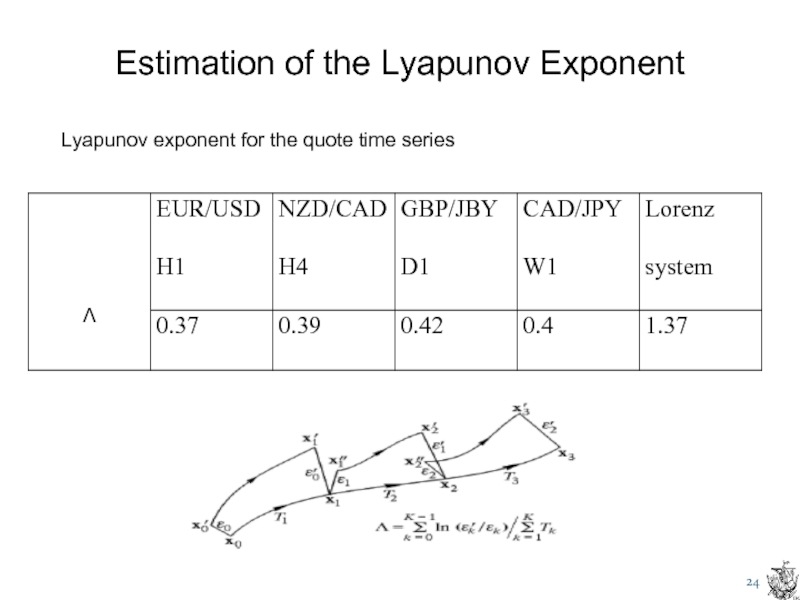
- 16. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЯ ЛЯПУНОВА
- 17. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЯ ЛЯПУНОВА
- 18. Реализации ЭЭГ лабораторных животных 1)Бодрствование 2)Медленный
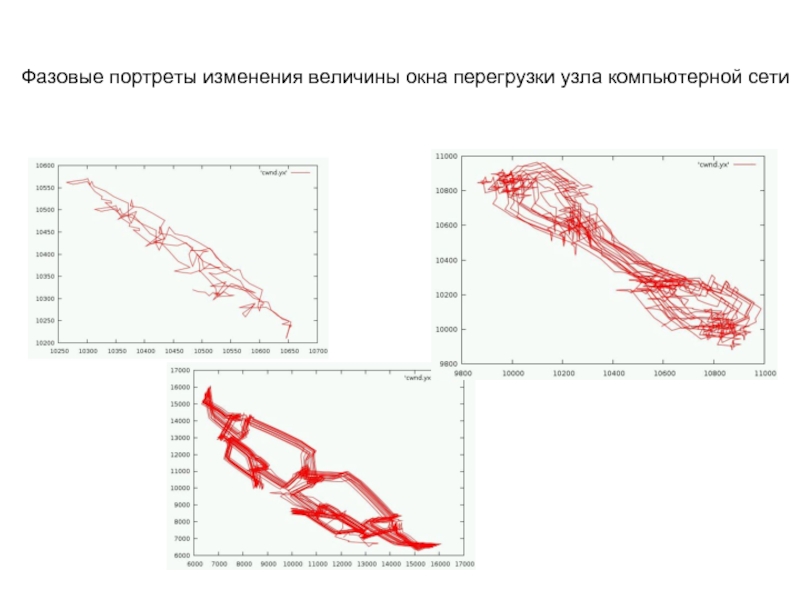
- 19. Фазовые портреты изменения величины окна перегрузки узла компьютерной сети
- 20. EUR/USD, time frame H1. NZD/CAD,
- 21. Reconstructed Attractors for Currency Quote Time Series
- 22. Estimation of the Correlation Dimension for quote
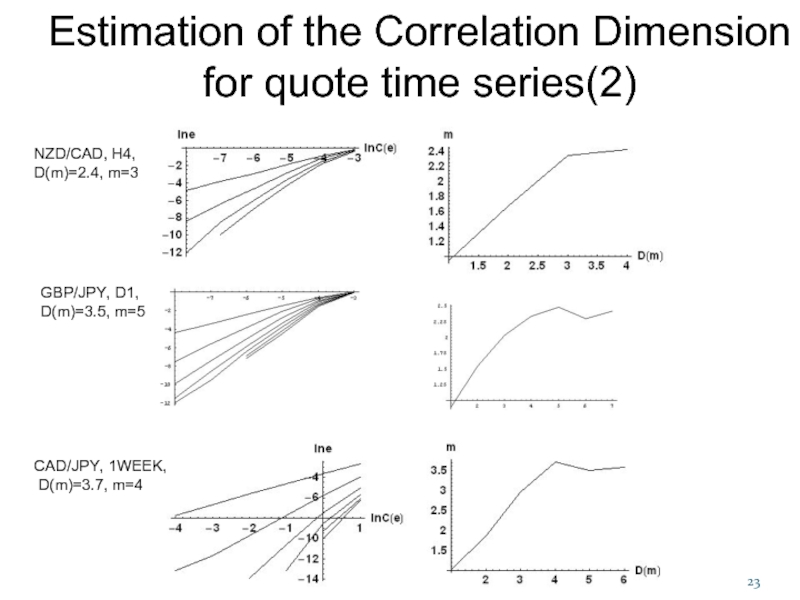
- 23. NZD/CAD, H4, D(m)=2.4, m=3 GBP/JPY, D1,
- 24. Estimation of the Lyapunov Exponent Lyapunov exponent for the quote time series
Слайд 1ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ ПО ВРЕМЕННОЙ РЕАЛИЗАЦИИ
Теоретически теория и практика - одно
Слайд 2 Пусть мы имеем записанную реализацию x = x(t) или, при наличии
Можно ли из ее анализа заключить, произведена ли реализация динамической системой или это просто случайный шумовой сигнал?
Если это динамическая система, то что можно сказать о ее свойствах и характеристиках — сколько переменных необходимо для задания состояния, какова фрактальная размерность аттрактора, отвечающего за наблюдаемый режим, хаотический ли он, можно ли сконструировать модель в виде дифференциальных уравнений или отображений, которая позволяла бы адекватно воспроизвести наблюдаемую временную зависимость и прогнозировать будущее состояние системы?
Анализ реализации
Слайд 3РЕКОНСТРУКЦИЯ АТТРАКТОРА
Главная идея применения методов хаотической динамики к анализу временных рядов
Слайд 8РЕКОНСТРУКЦИЯ СЛУЧАЙНОГО СИГНАЛА
Значения τ
в долях от единицы времени
0.02 (а), 0.25
Слайд 9РАЗМЕРНОСТЬ ВЛОЖЕНИЯ
Размерность вложения m –
минимальная
целая размерность фазового
пространства, которое
Слайд 14КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ
dc≤ m
Размерность вложения m – это
АТТРАКТОР ЛОРЕНЦА
Слайд 15КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ
Для случайных процессов, т.е. порожденных системой с
числом степеней свободы, фрактальная размерность является целым
числом и ее значение приближенно равняется размерности
фазового пространства, в котором она вычисляется .
Шумовой сигнал
Слайд 18Реализации ЭЭГ лабораторных животных
1)Бодрствование
2)Медленный сон
3)Парадоксальный сон
АНАЛИЗ РЕЗУЛЬТАТОВ
Восстановленные псевдофазовые портреты
τ=500
τ=480
τ=420
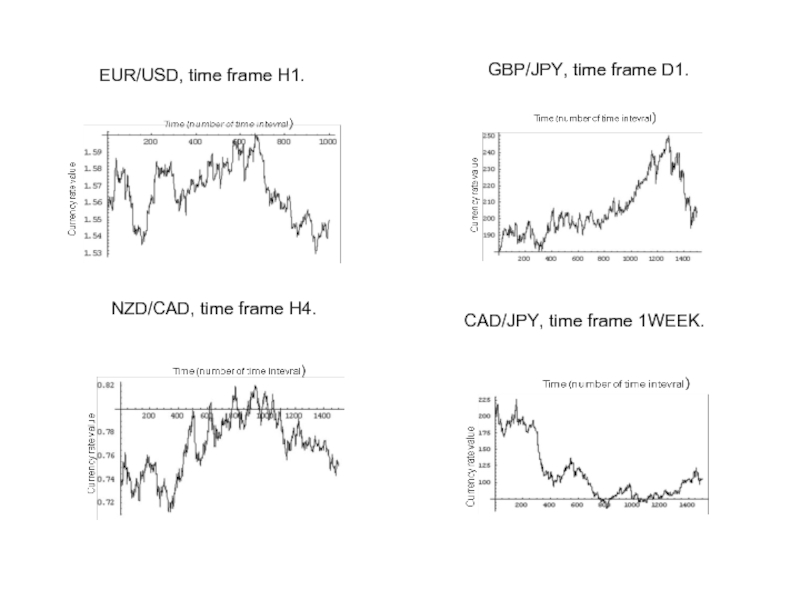
Слайд 20
EUR/USD, time frame H1.
NZD/CAD, time frame H4.
GBP/JPY, time frame D1.
CAD/JPY, time
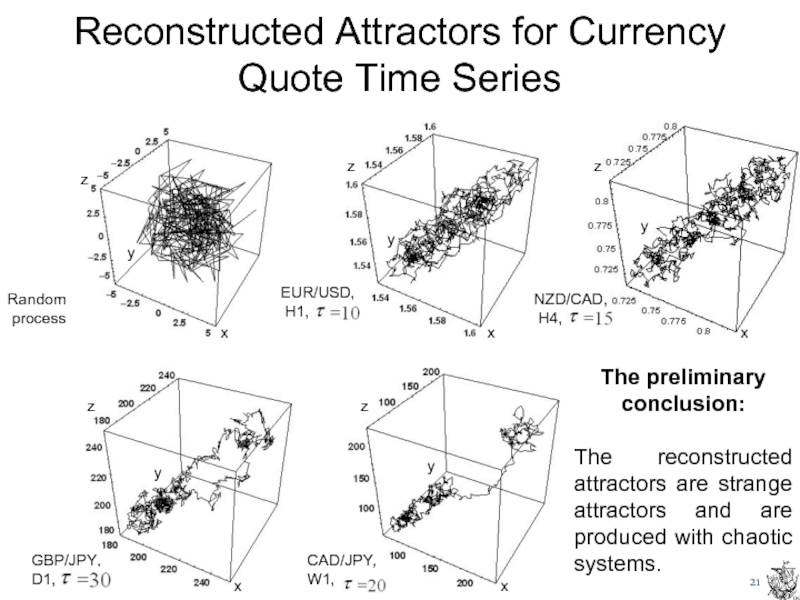
Слайд 21Reconstructed Attractors for Currency Quote Time Series
Random
process
EUR/USD,
H1,
NZD/CAD,
GBP/JPY,
D1,
CAD/JPY,
W1,
The preliminary conclusion:
The reconstructed attractors are strange attractors and are produced with chaotic systems.
x
y
x
x
y
y
y
y
x
x
z
z
z
z
z
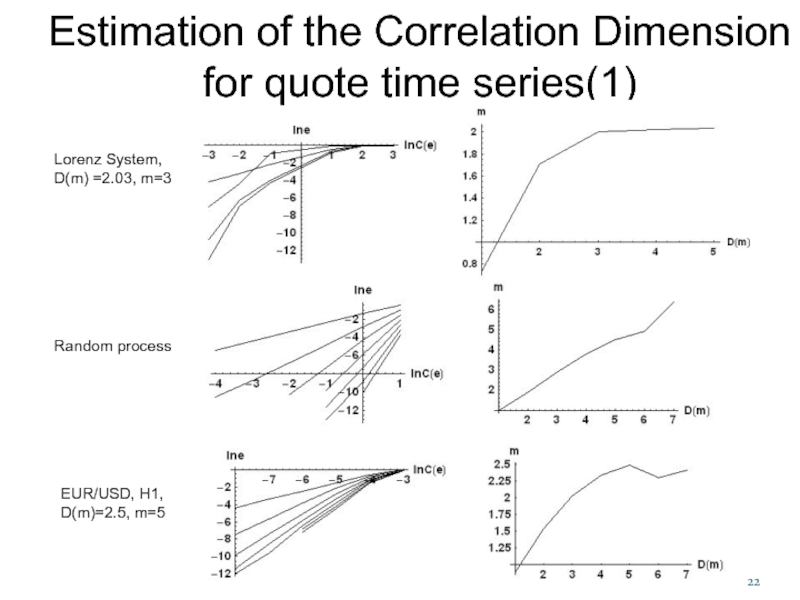
Слайд 22Estimation of the Correlation Dimension for quote time series(1)
Lorenz System,
D(m)
Random process
EUR/USD, H1,
D(m)=2.5, m=5