- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гиперболический хаос презентация
Содержание
- 1. Гиперболический хаос
- 2. Содержание Введение. Базовые понятия Аттракторы
- 3. 1. Введение Исследование устойчивости, изучение роли
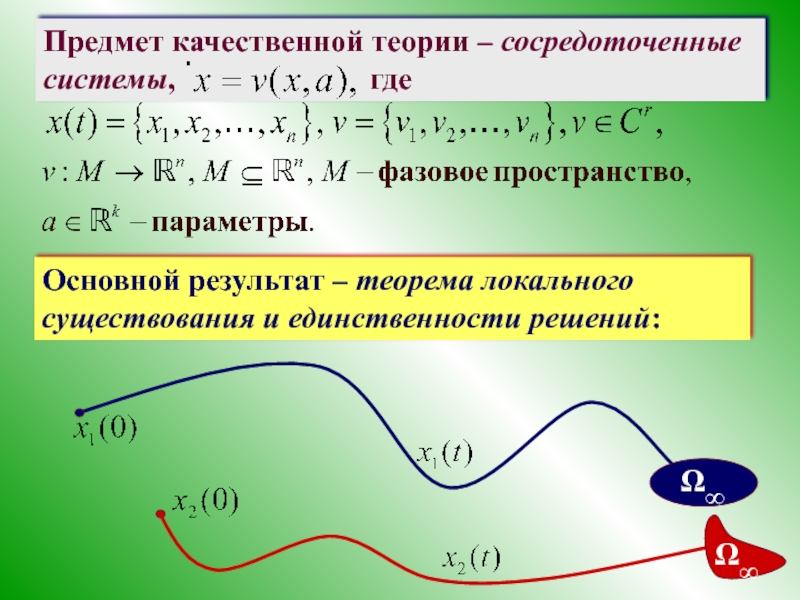
- 4. Предмет качественной теории – сосредоточенные системы,
- 5. Таким образом, можно предложить геометрический подход
- 6. Поток
- 7. Говорят, что свойство динамической системы яв-ляется грубым
- 8. Диссипация
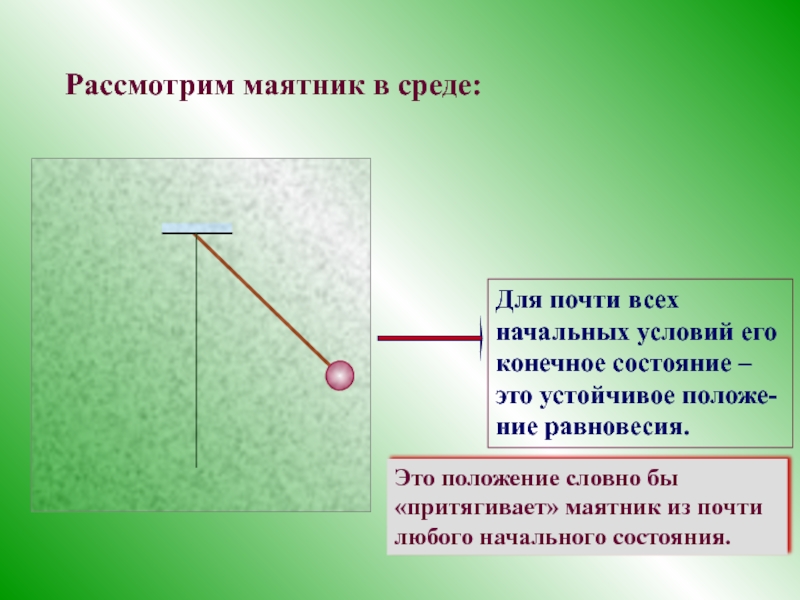
- 9. Рассмотрим маятник в среде: Это
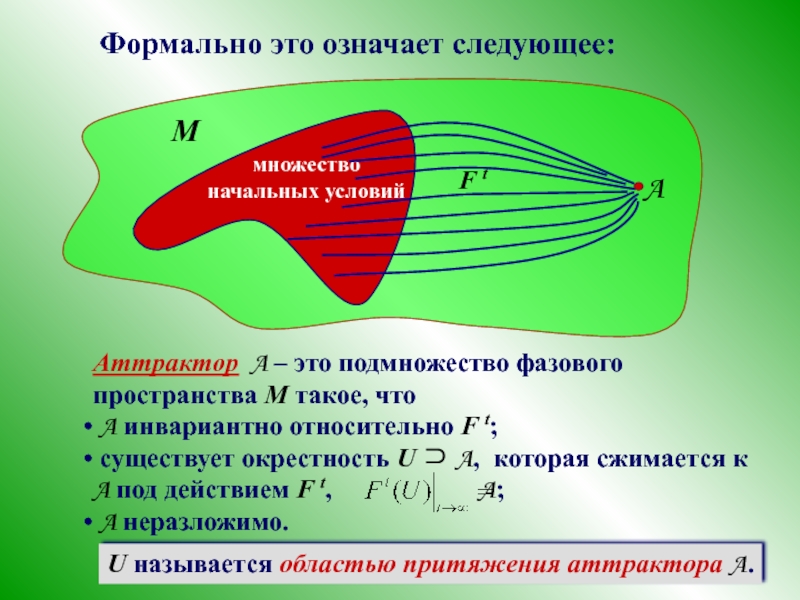
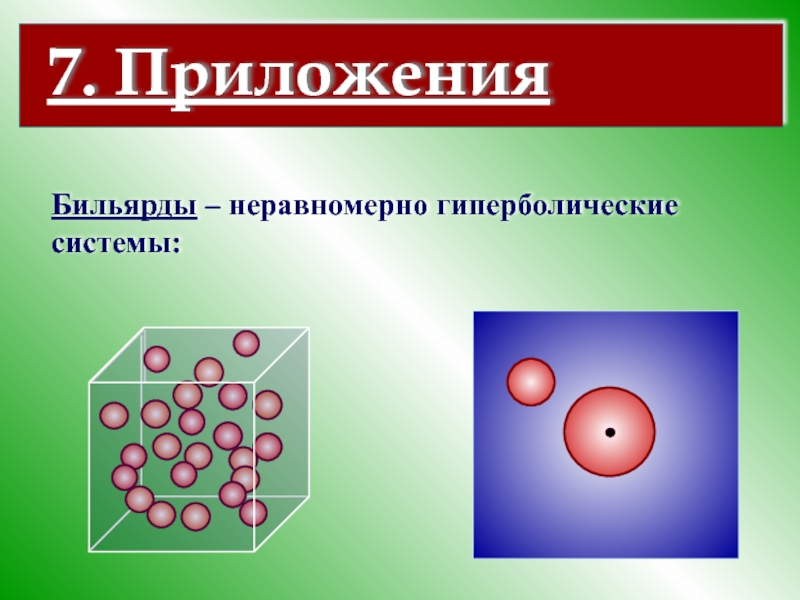
- 10. Формально это означает следующее: U называется областью притяжения аттрактора A. F t
- 11. Рассмотрим систему: Точки ,
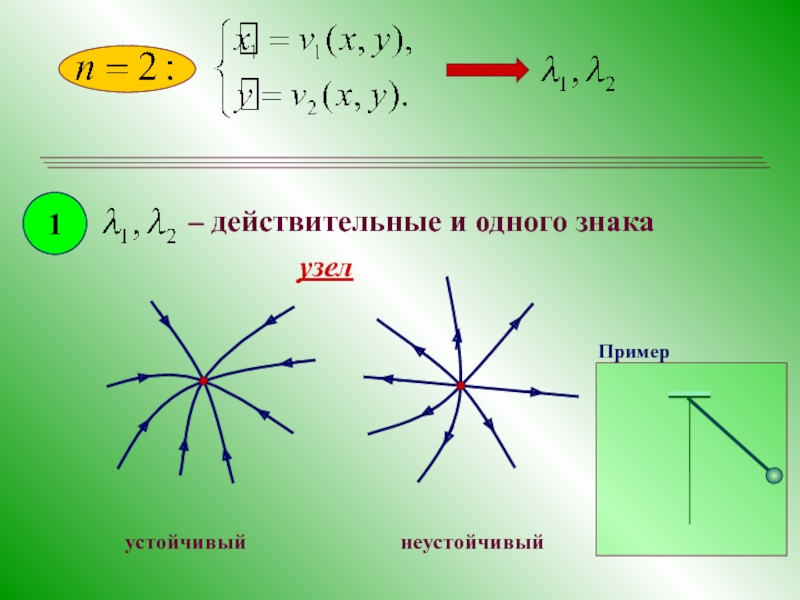
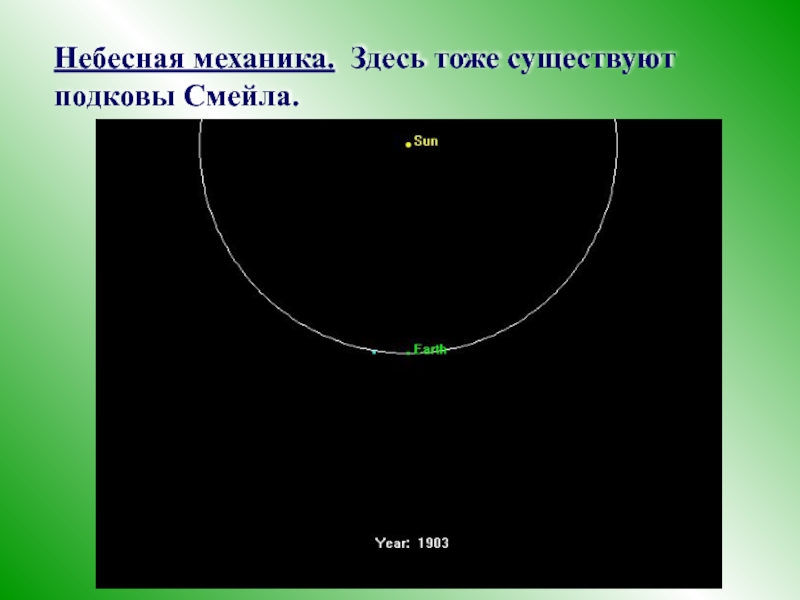
- 12. 1 – действительные и одного знака узел устойчивый неустойчивый Пример
- 13. 2 – действительные и разных знаков седло 3 фокус неустойчивый устойчивый Пример
- 14. 4 – чисто мнимые центр
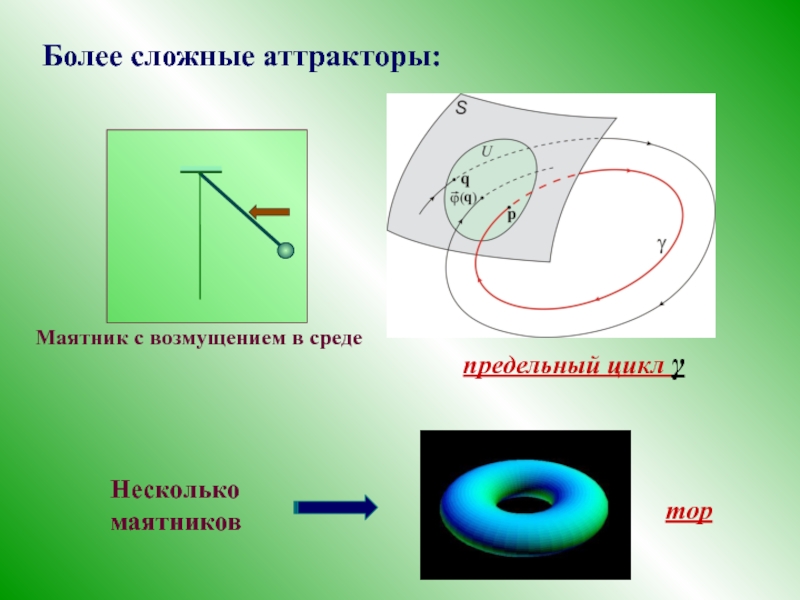
- 16. Более сложные аттракторы: Маятник с возмущением в среде
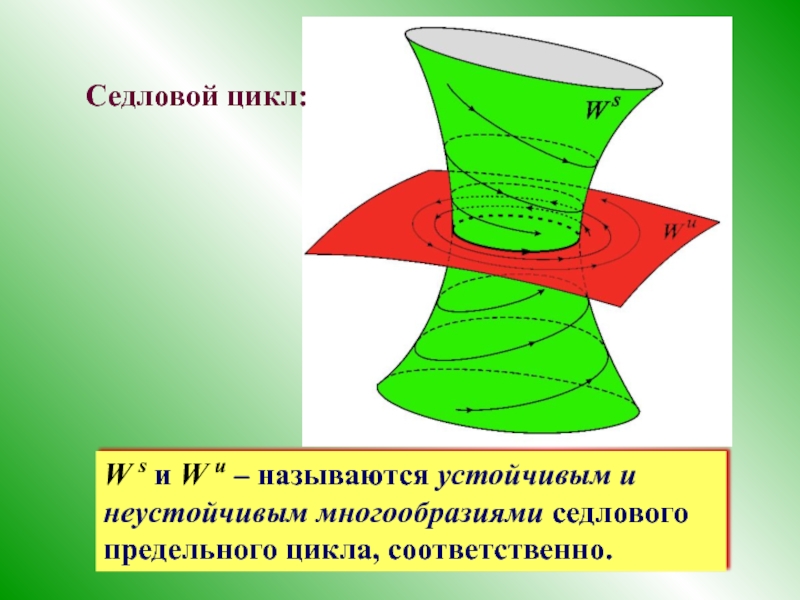
- 17. Седловой цикл: W s и W u
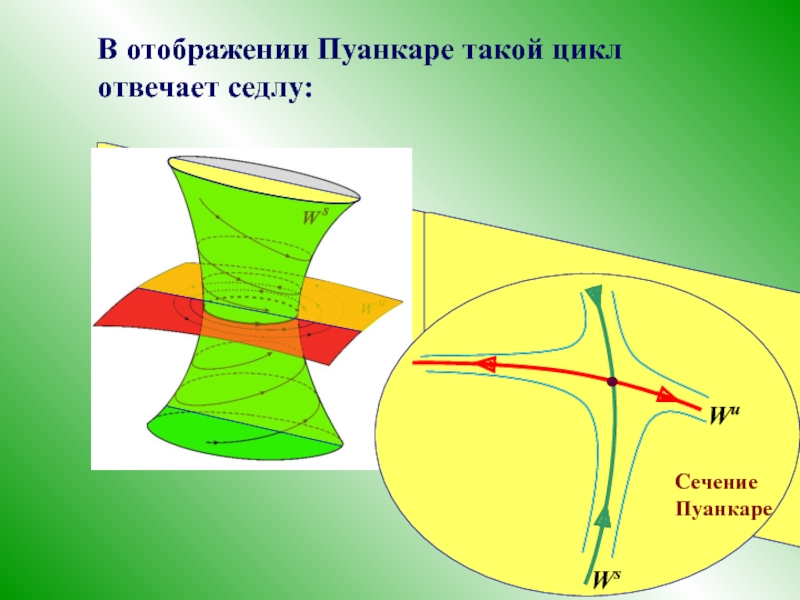
- 18. В отображении Пуанкаре такой цикл отвечает седлу:
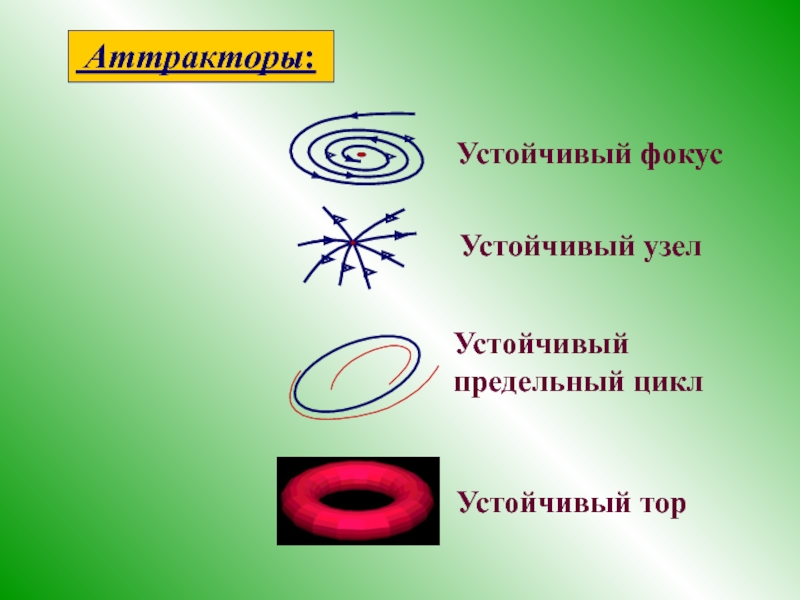
- 19. Устойчивый узел Устойчивый фокус Аттракторы: Устойчивый предельный цикл Устойчивый тор
- 20. 3. Хаос Пусть M – метрическое
- 21. Гиперболические множества Такие множества служат хорошим примером для понимания «устройства» хаотических систем.
- 22. W
- 23. Если вдоль траектории γ оценки ухудшаются, т.е.
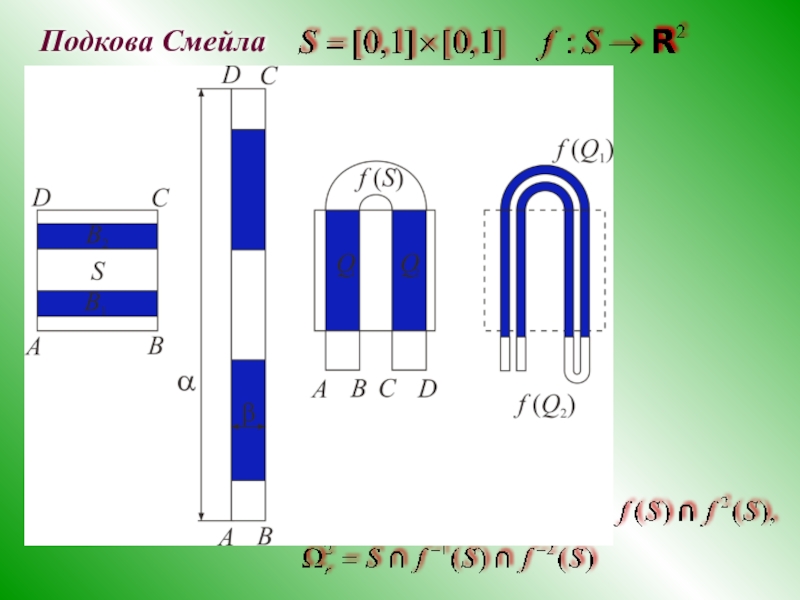
- 24. Подкова Смейла
- 25. Точки p, которые всегда остаются в S,
- 26. 4. Гомоклинические структуры Пусть система имеет
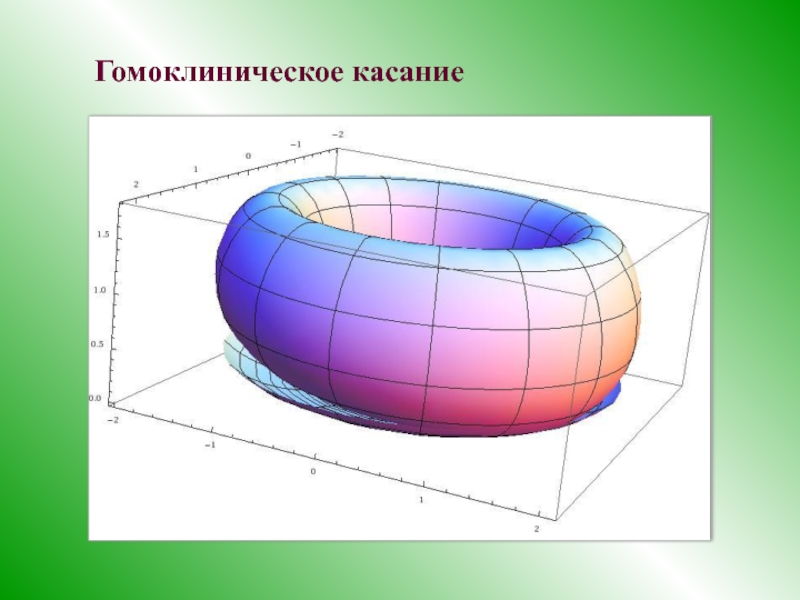
- 29. Гомоклиническое касание
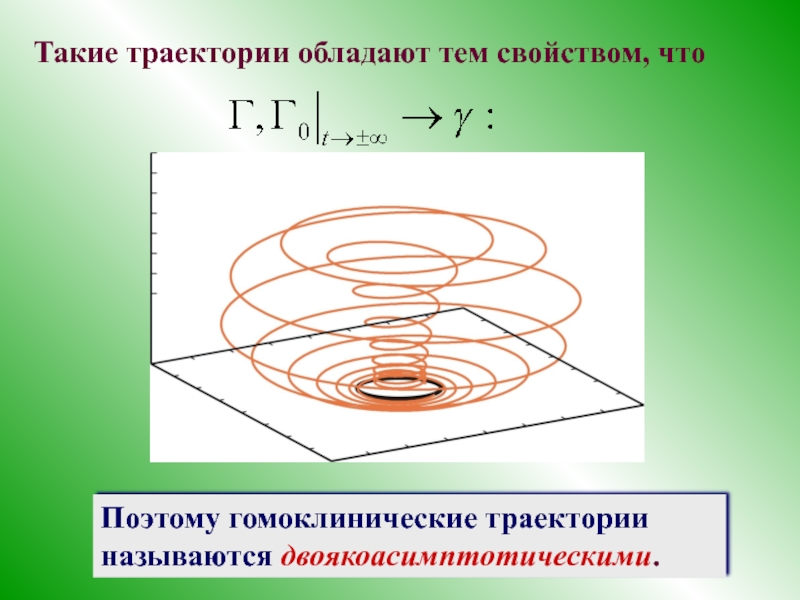
- 30. Такие траектории обладают тем свойством, что Поэтому гомоклинические траектории называются двоякоасимптотическими.
- 31. Из наличия одной гомоклинической траектории следует существование
- 32. Рождение подков Рассмотрим малую окрестность U гиперболической
- 33. Системы с гомоклиническими петлями негрубые. Поэтому
- 34. U – окрестность точки O: W s
- 35. Отображение преобразует область
- 36. Таким образом, горизонтальные полосы на D отображают-ся
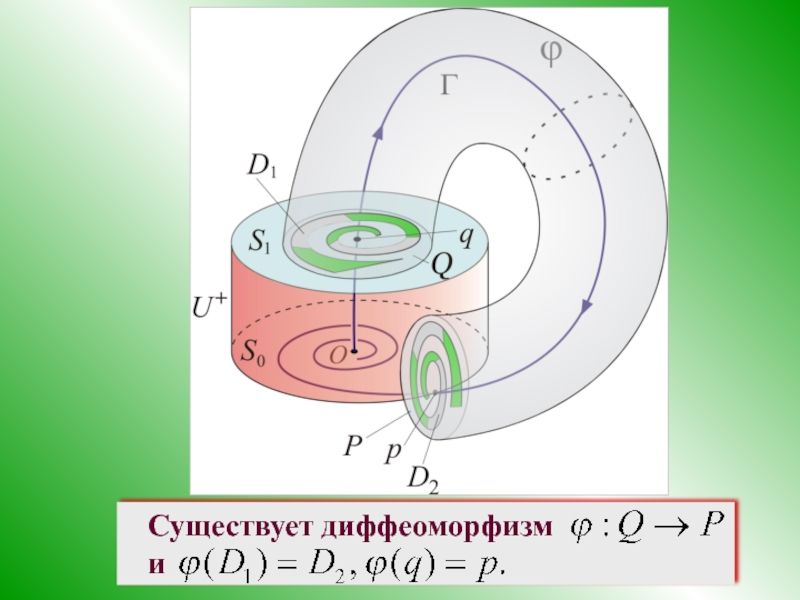
- 37. Существует диффеоморфизм
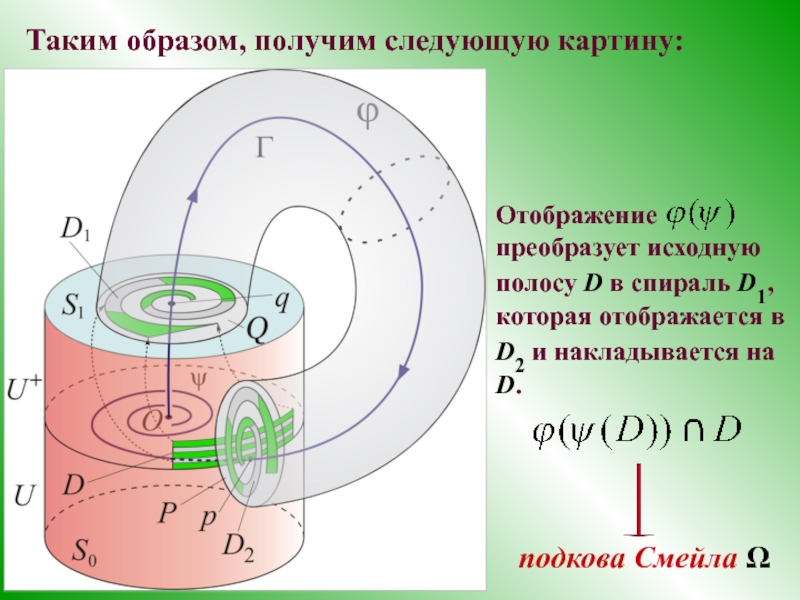
- 38. Таким образом, получим следующую картину: подкова Смейла Ω
- 39. 5. Дикие гиперболи-ческие множества Системы с
- 40. В зависимости от геометрии, в системе возможны
- 41. II тип Множество Δ траекторий в малой
- 42. III тип Множество Δ содержит нетривиальные гиперболические
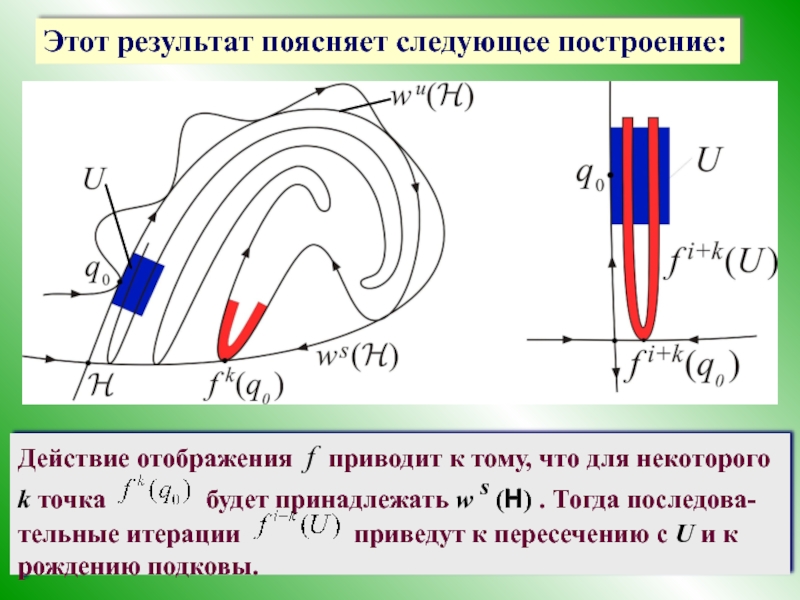
- 43. Этот результат поясняет следующее построение: Действие отображения
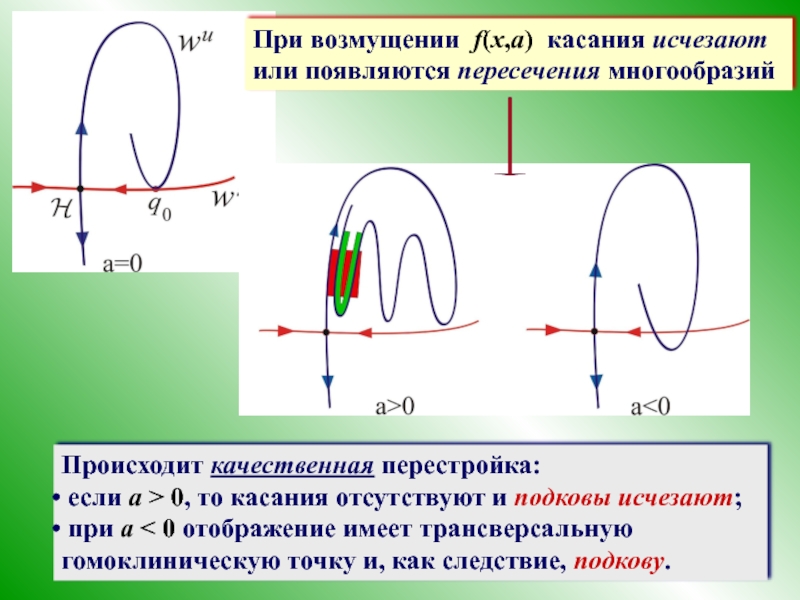
- 44. При возмущении f(x,a) касания исчезают или появляются пересечения многообразий
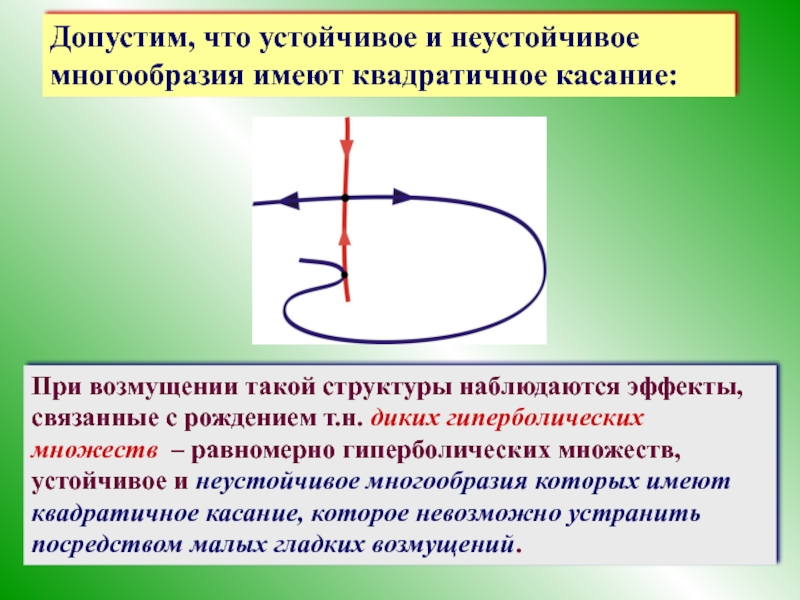
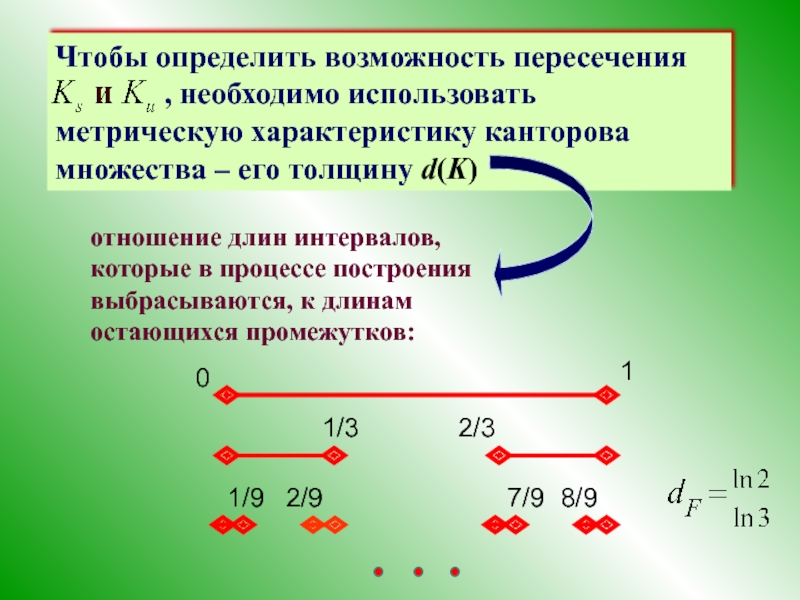
- 45. Допустим, что устойчивое и неустойчивое многообразия имеют
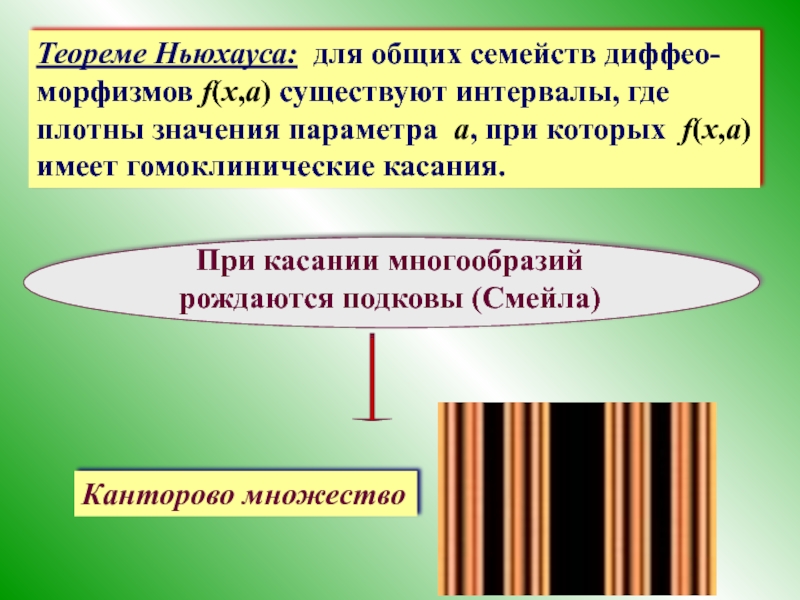
- 46. Теореме Ньюхауса: для общих семейств диффео-морфизмов f(x,a)
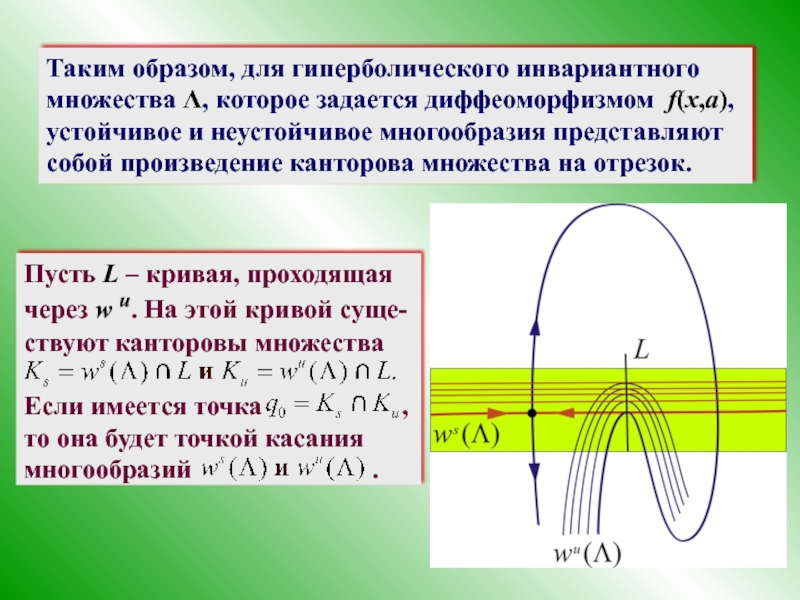
- 47. Таким образом, для гиперболического инвариантного множества Λ,
- 50. Сложность динамики систем с гомоклиническими касаниями
- 51. При гладких возмущениях систем с гомоклиническими касаниями могут рождаться циклы произвольно высоких порядков вырождения.
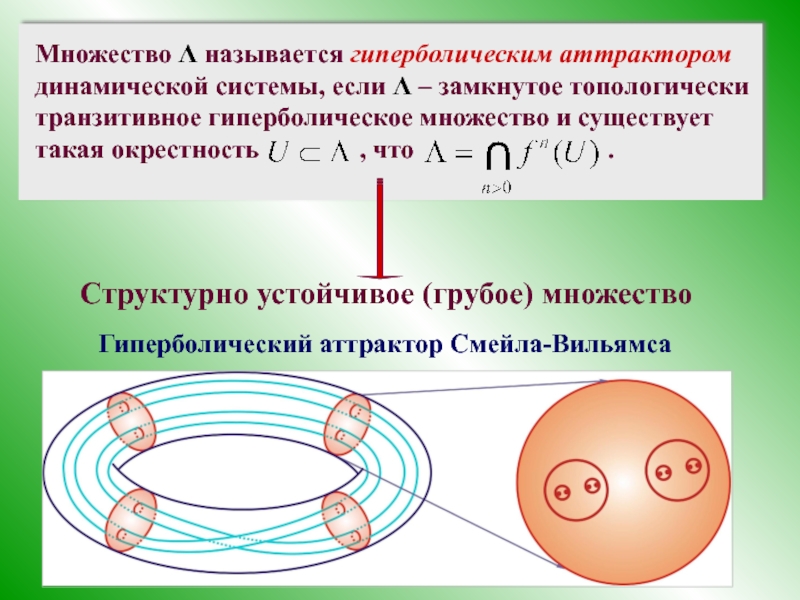
- 52. 6. Гипреболические и другие аттракторы Аттрактор
- 53. Странные аттракторы обладают некоторой степенью гиперболичности, однако
- 54. Обычно считается, что динамическая система обладает странным
- 55. Структурно устойчивое (грубое) множество Гиперболический аттрактор Смейла-Вильямса
- 56. Гиперболический аттрактор Плыкина
- 57. Адекватным математическим образом наблюдаемого разви-того хаотического
- 58. 7. Приложения Бильярды – неравномерно гиперболические
- 59. Система Дуффинга. В такой системе существуют подковы Смейла.
- 60. Небесная механика. Здесь тоже существуют подковы Смейла.
- 61. Нелинейный маятник. Здесь наблюдаются гомо- и гетероклинические структуры. фазовое пространство
- 62. Основные достижения теории хаотических динамических систем:
- 63. Спасибо за внимание!
Слайд 2Содержание
Введение. Базовые понятия
Аттракторы
Хаос
Гомоклинические структуры
Дикие гиперболические множества
Приложения
Слайд 3
1. Введение
Исследование устойчивости, изучение роли инвариантных многообразий, анализ геометрической структуры траекторий,
Основная идея – качественное интегрирование
Качественная теория
Слайд 5Таким образом, можно предложить геометрический подход
Эта функция определена для и
Слайд 6
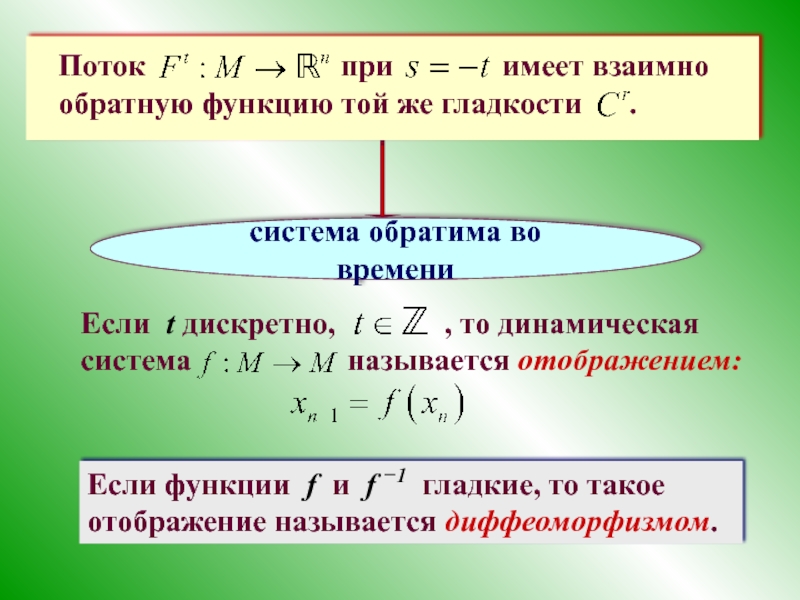
Поток
система обратима во времени
Если t дискретно, , то динамическая система называется отображением:
Если функции f и f −1 гладкие, то такое отображение называется диффеоморфизмом.
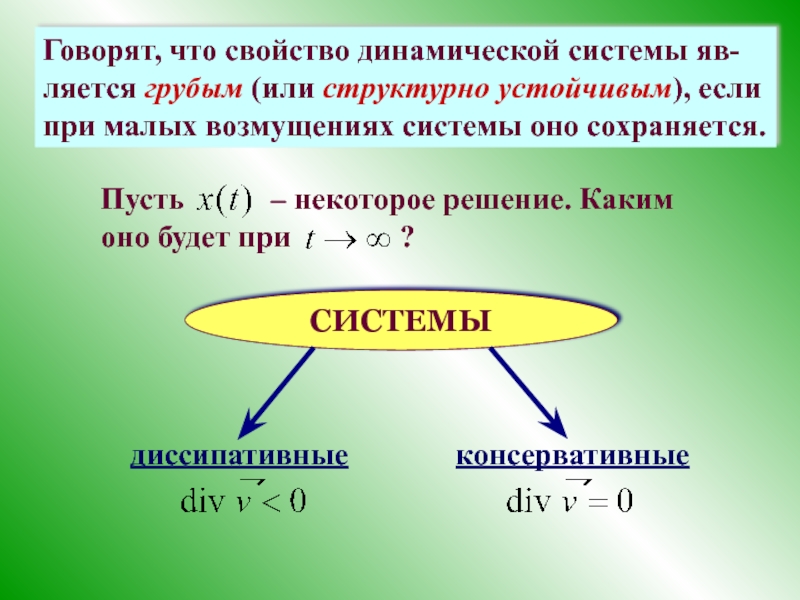
Слайд 7Говорят, что свойство динамической системы яв-ляется грубым (или структурно устойчивым), если
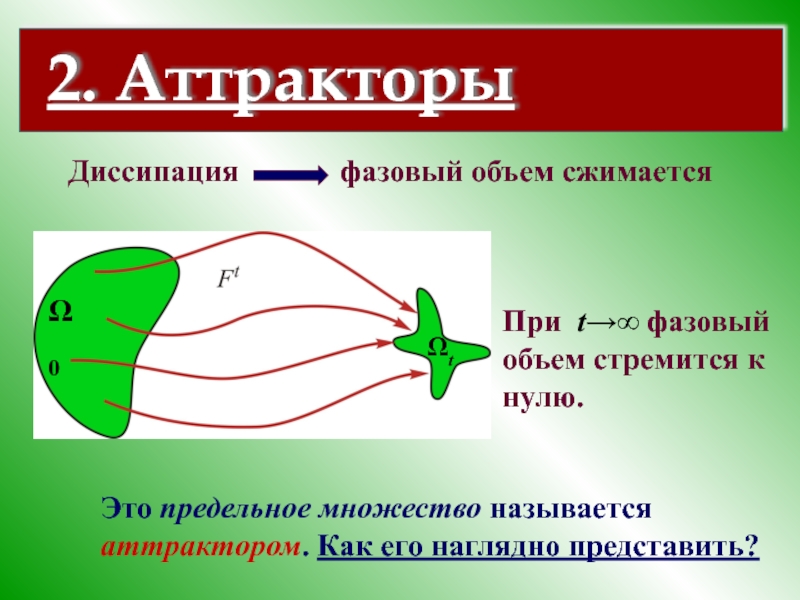
Слайд 8Диссипация фазовый объем сжимается
При t→∞
Это предельное множество называется аттрактором. Как его наглядно представить?
2. Аттракторы
Слайд 9Рассмотрим маятник в среде:
Это положение словно бы «притягивает» маятник из
Слайд 11
Рассмотрим систему:
Точки , в которых
неустойчивое
устойчивое
Слайд 15
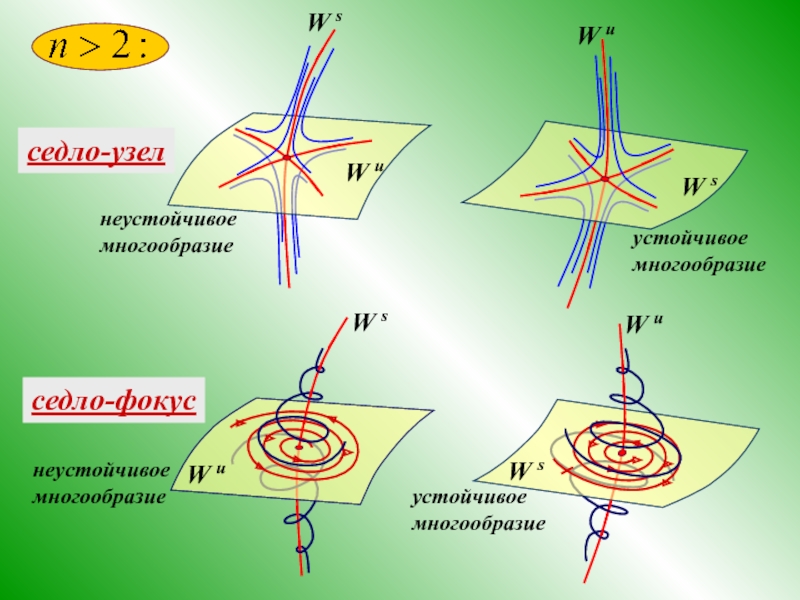
седло-узел
неустойчивое многообразие
устойчивое
многообразие
W s
W u
седло-фокус
неустойчивое многообразие
устойчивое
многообразие
W s
W u
W s
W u
Слайд 17Седловой цикл:
W s и W u – называются устойчивым и неустойчивым
Слайд 20
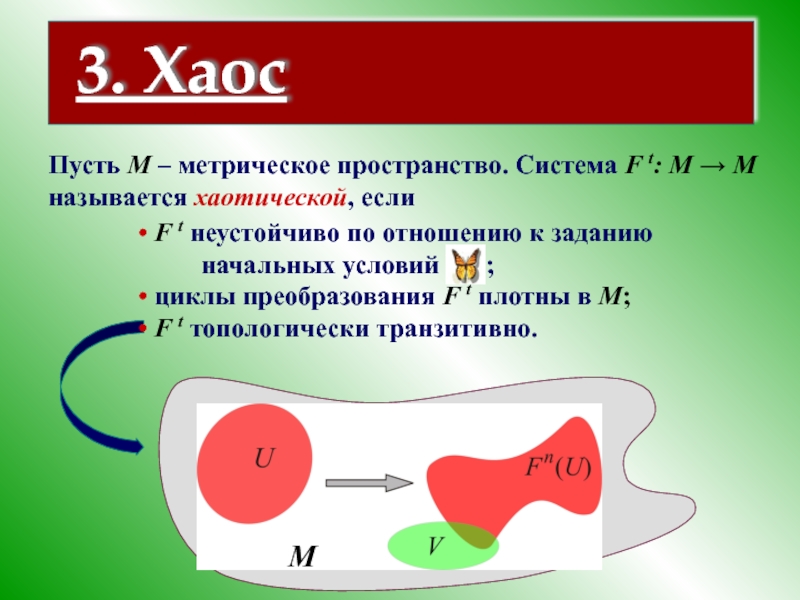
3. Хаос
Пусть M – метрическое пространство. Система F t: M →
F t неустойчиво по отношению к заданию
начальных условий ;
циклы преобразования F t плотны в M;
F t топологически транзитивно.
Слайд 21Гиперболические множества
Такие множества служат хорошим примером для понимания «устройства» хаотических систем.
Слайд 22
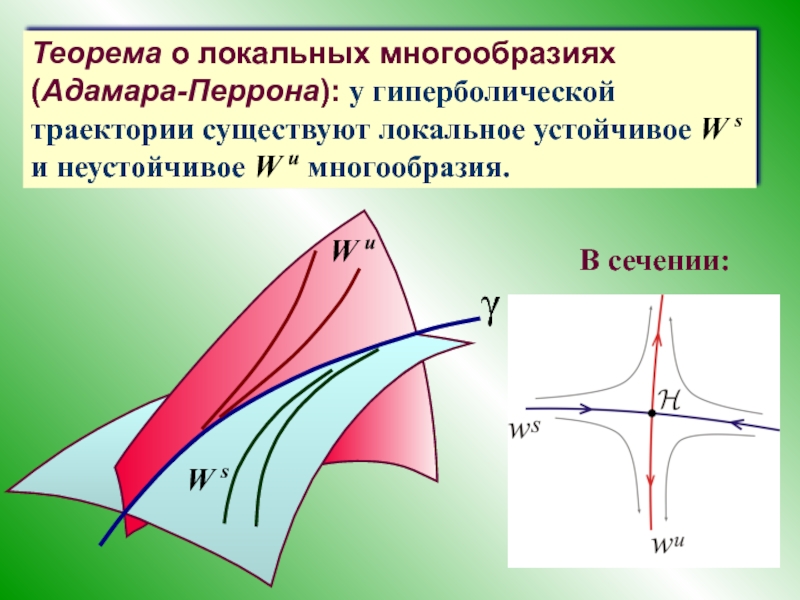
W s
W u
γ
Теорема о локальных многообразиях (Адамара-Перрона): у гиперболической траектории существуют
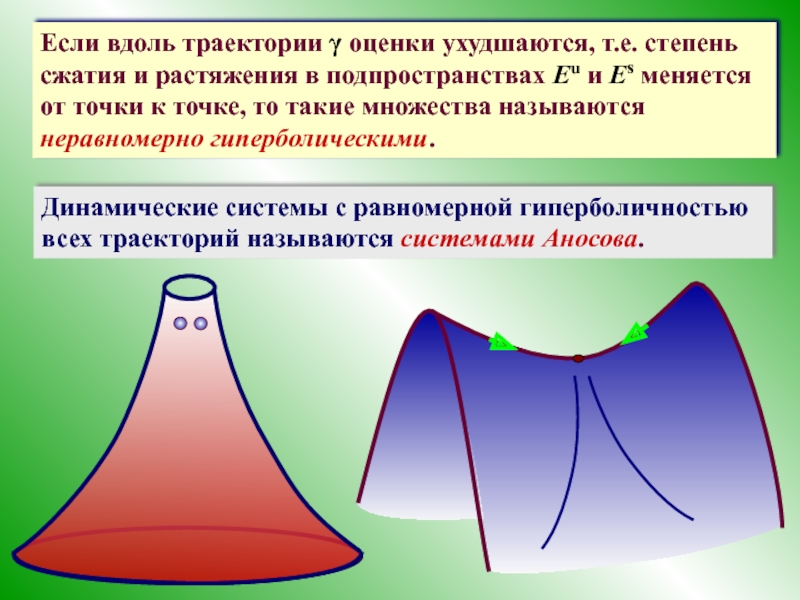
Слайд 23Если вдоль траектории γ оценки ухудшаются, т.е. степень сжатия и растяжения
Динамические системы с равномерной гиперболичностью всех траекторий называются системами Аносова.
Слайд 25Точки p, которые всегда остаются в S, образуют канторово множество. Это
Множество Ω содержит
циклы всевозможных периодов;
плотную траекторию;
несчетное множество непериодических траекторий.
ХАОС
Слайд 26
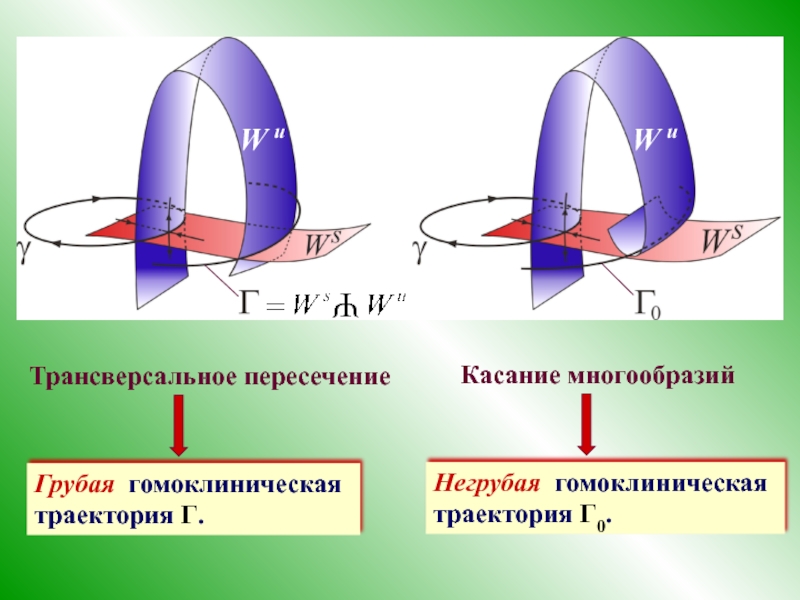
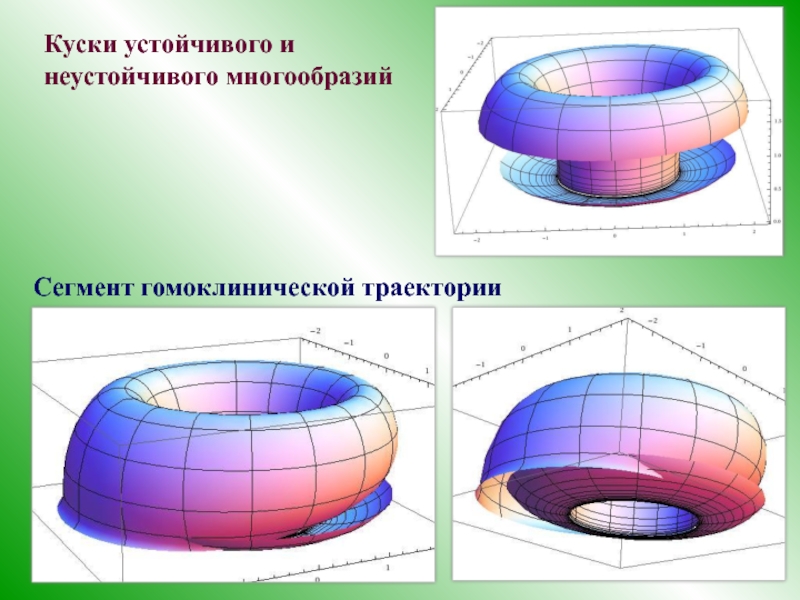
4. Гомоклинические структуры
Пусть система имеет седловой цикл с устойчивым и неустойчивым
γ
W u
W s
Слайд 30Такие траектории обладают тем свойством, что
Поэтому гомоклинические траектории называются двоякоасимптотическими.
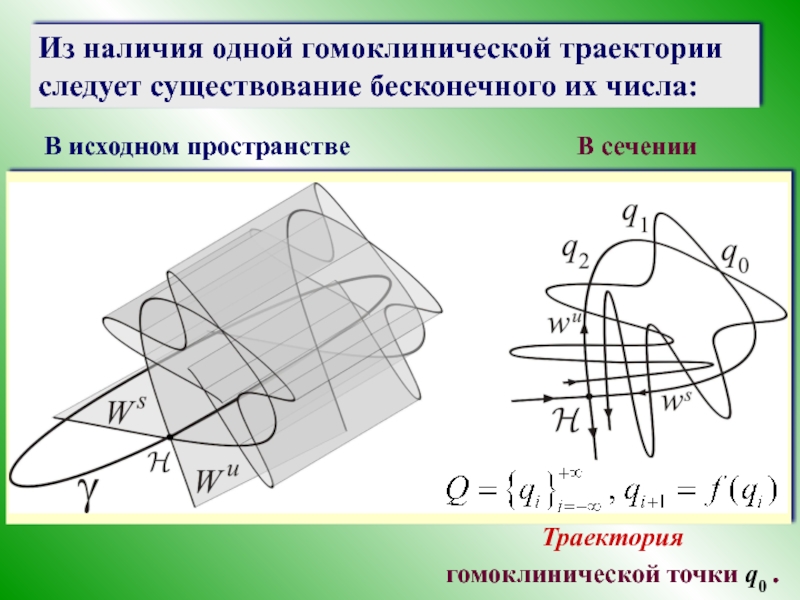
Слайд 31Из наличия одной гомоклинической траектории следует существование бесконечного их числа:
В исходном
В сечении
Траектория гомоклинической точки q0 .
Слайд 32Рождение подков
Рассмотрим малую окрестность U гиперболической точки H:
U
Следствие. Наличие гомоклинической точки
Слайд 33
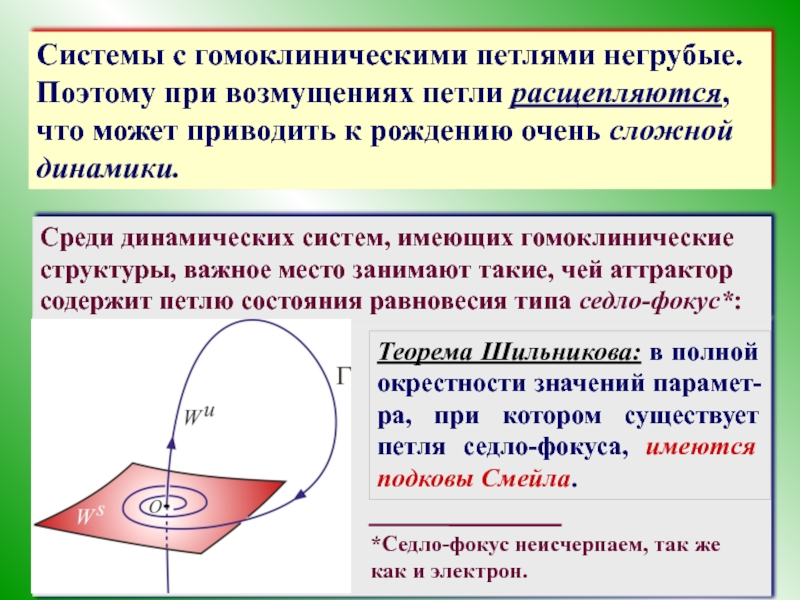
Системы с гомоклиническими петлями негрубые. Поэтому при возмущениях петли расщепляются, что
Среди динамических систем, имеющих гомоклинические структуры, важное место занимают такие, чей аттрактор содержит петлю состояния равновесия типа седло-фокус*:
Слайд 34U – окрестность точки O:
W s делит U на U+ и
Для
Рассмотрим рождение подковы из седло-фокуса Γ.
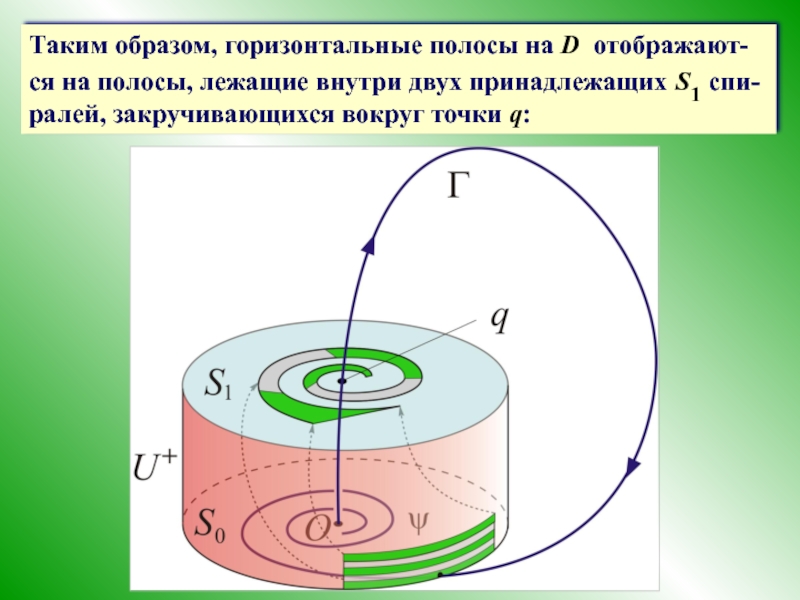
Слайд 36Таким образом, горизонтальные полосы на D отображают-ся на полосы, лежащие внутри
Слайд 39
5. Дикие гиперболи-ческие множества
Системы с касаниями W s и W u
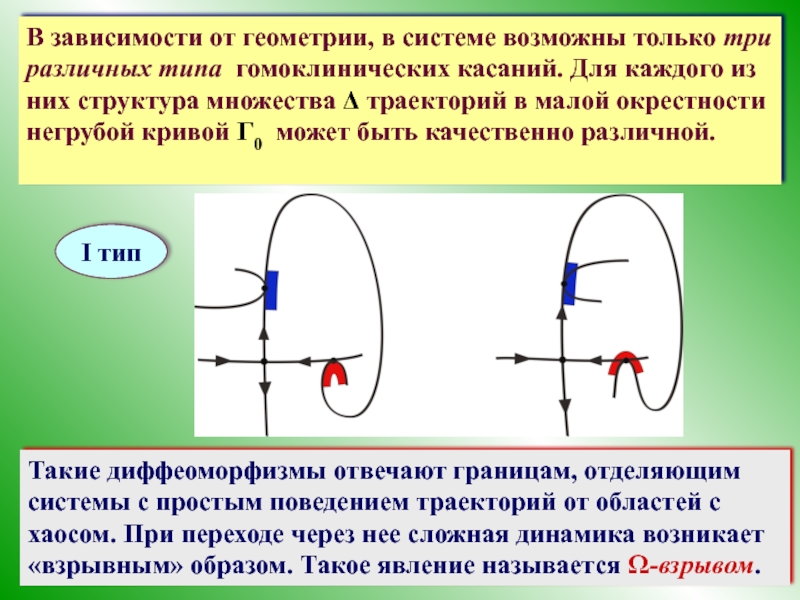
Слайд 40В зависимости от геометрии, в системе возможны только три различных типа
I тип
Такие диффеоморфизмы отвечают границам, отделяющим системы с простым поведением траекторий от областей с хаосом. При переходе через нее сложная динамика возникает «взрывным» образом. Такое явление называется Ω-взрывом.
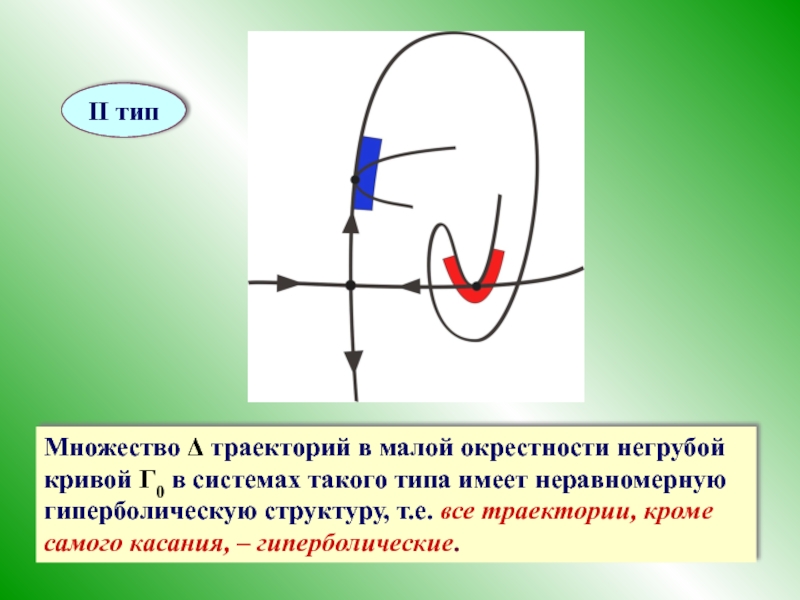
Слайд 41II тип
Множество Δ траекторий в малой окрестности негрубой кривой Γ0 в
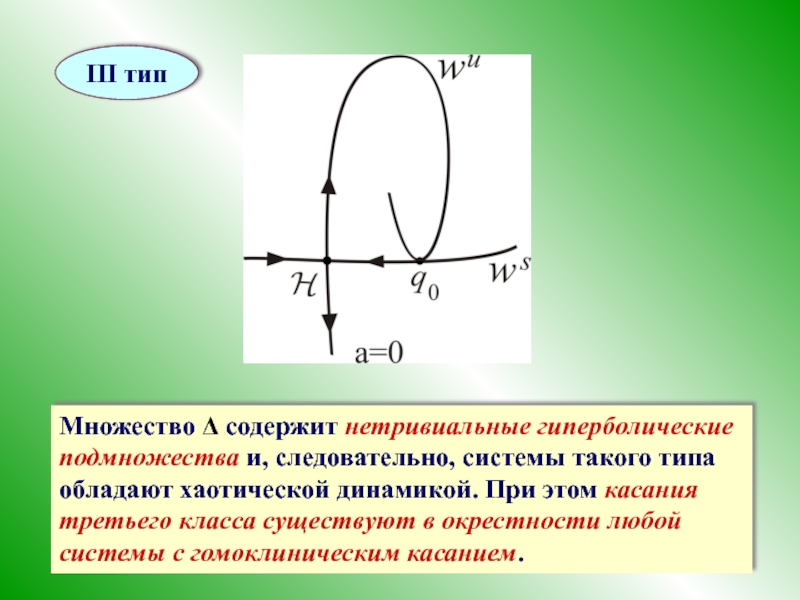
Слайд 42III тип
Множество Δ содержит нетривиальные гиперболические подмножества и, следовательно, системы такого
Слайд 43Этот результат поясняет следующее построение:
Действие отображения f приводит к тому, что
Слайд 45Допустим, что устойчивое и неустойчивое
многообразия имеют квадратичное касание:
При возмущении такой структуры
Слайд 46Теореме Ньюхауса: для общих семейств диффео-морфизмов f(x,a) существуют интервалы, где плотны
Слайд 47Таким образом, для гиперболического инвариантного множества Λ, которое задается диффеоморфизмом f(x,a),
Слайд 50Сложность динамики систем с гомоклиническими касаниями
В областях Нюьхауса плотны системы,
Здесь существует счетное множество седловых и абсолютно неустойчивых циклов.
Такие системы имеют счетное множество устойчивых и неустойчивых инвариантных торов, сосуществующих со счетным множест-вом седловых, устойчивых и абсолютно неустой-чивых циклов.
Слайд 51При гладких возмущениях систем с гомоклиническими касаниями могут рождаться циклы произвольно
Слайд 52
6. Гипреболические и другие аттракторы
Аттрактор динамической системы называется странным, если он
Слайд 53Странные аттракторы обладают некоторой степенью гиперболичности, однако эта гиперболичность имеет иную
В областях Ньюхауса могут быть плотны хаотические системы со счетным числом странных аттракторов. Более того, в окрестности семейства диффеоморфизмов, имеющего гомоклиническое касание устойчивого и неустойчивого многообразий гипреболической точки, могут существовать подмножества систем, обладающих странными аттракторами.
Слайд 54Обычно считается, что динамическая система обладает странным аттрактором, если в ее
гомо- и гетероклиничностью,
фрактальностью,
наличием положительного ляпуновского показателя,
непрерывностью спектра,
бифуркациями удвоения периода и т.п.
Понятие «странный аттрактор» имеет собирательный смысл
Таким образом, этот термин является скорее парадигмой, чем характеристикой какого-то
математического объекта.
Слайд 57
Адекватным математическим образом наблюдаемого разви-того хаотического поведения физической системы может слу-жить
возмущений. Этот термин связывается с существованием инвариантной меры.
Аттрактор динамической системы называется стохастическим, если динамическая система обладает перемешиванием.
Однако большинство хаотических аттракторов принадлежит к квазистохастическому типу (т.е. они являются так называе-мыми квазиаттракторами). Такие аттракторы содержат бесконечное множество устойчивых периодических траекто-рий. Примеры: аттракторы Рёслера, Чуа и др. в системах ОДУ
Слайд 61Нелинейный маятник. Здесь наблюдаются гомо- и гетероклинические структуры.
фазовое пространство
Слайд 62Основные достижения теории хаотических динамических систем:
доказано, что даже очень простые
достигнут значительный прогресс в понимании происхождения случайности в газе твердых сфер и, как следствие, в обосновании эргодический гипотезы Больцмана;
удалось частично решить проблему возникновения необратимости в обратимых детерминированных уравнениях движения;
хаос рождается универсальными путями, независимо от природы системы;
случайность может быть обусловлена как внутренними свойствами, так и внешними факторами. При этом всегда можно отличить случайное поведение систем от детерминированного хаоса.
Наконец, нельзя не сказать и об эстетической стороне результатов теории хаоса. Как заметил Д.Рюэль, это область исследования, в которой будут открыты новые гармонии.