- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гидрогазодинамика. Элементы теории гидродинамического пограничного слоя. (Тема 1. Лекции 3,4) презентация
Содержание
- 1. Гидрогазодинамика. Элементы теории гидродинамического пограничного слоя. (Тема 1. Лекции 3,4)
- 2. § 6. Элементы теории гидродинамического пограничного слоя
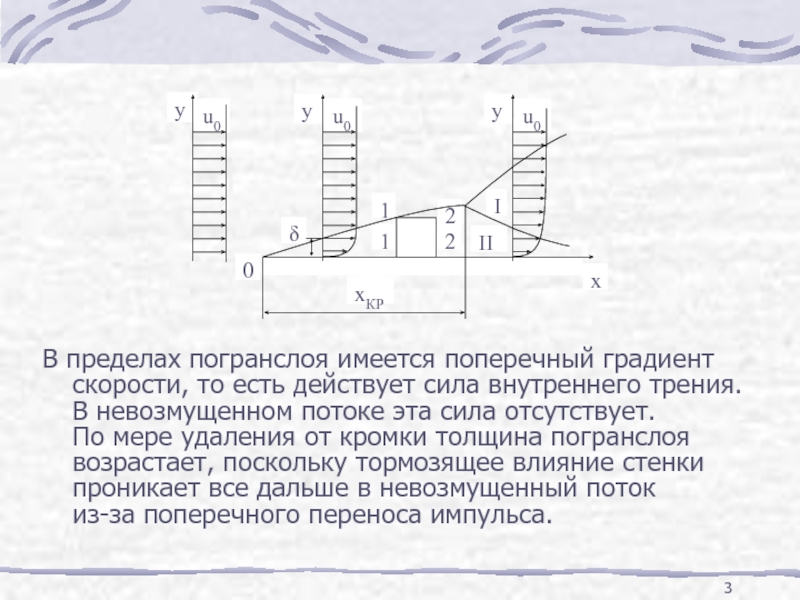
- 3. В пределах погранслоя имеется поперечный градиент скорости,
- 4. Из-за возрастания толщины погранслоя уменьшается среднее значение
- 5. Найдем уравнения, описывающие стационарное движение несжимаемой жидкости
- 6. Рассматриваемое двумерное течение описывается следующей системой уравнений:
- 7. Оценим порядок входящих в систему величин и
- 8. Из самых общих соображений можно заключить,
- 9. Второе уравнение вырождается в условие постоянства давления
- 10. Неизвестными функциями в системе уравнений Прандтля являются
- 11. Уравнения Прандтля для плоской поверхности
- 12. В стационарном потоке несжимаемой жидкости вблизи плоской
- 13. Определим результирующий поток импульса через поверхность выделенного
- 14. На расстоянии dx эта величина получит приращение
- 15. Так как жидкость несжимаема, то количество жидкости,
- 16. Подставляя выражения для потоков импульса, приводя подобные
- 17. Для ламинарного погранслоя с учетом формулы Ньютона
- 18. § 8. Расчет ламинарного пограничного слоя на
- 19. 3) при y = δ u
- 20. Подставим полученное выражение для u в уравнение
- 22. Разделим переменные и произведем сокращения:
- 23. Формула для δ позволяет найти u(x,y) и
- 24. § 9. Уравнение Бернулли Титульный лист
- 25. Рассмотрим элемент трубки тока, движение в котором
- 26. Умножая обе части уравнения на ρ, получим:
- 27. Величину α называют коэффициентом Кориолиса.
- 28. § 10. Потери давления на трение
- 29. При ламинарном режиме движения λ~1/Re. Так, для
- 30. Потери давления на местные сопротивления обусловлены, во-первых,
- 31. Считаем, что на всей площади левого сечения
- 32. В соответствии с уравнением неразрывности
- 34. Подставляя значение , получим:
Слайд 2§ 6. Элементы теории гидродинамического пограничного слоя
Пограничный слой – тонкая
Рассмотрим стационарное движение неограниченного потока жидкости с однородным распределением скорости u0 вдоль полубесконечной плоской поверхности (неограниченна в направлении оси z и в положительном направлении оси x). За кромкой поверхности, то есть при x>0, скорость на поверхности равна нулю, следовательно, вблизи поверхности образуется область, в пределах которой скорость изменяется от 0 на стенке до u0 на ее верхней границе.
Слайд 3В пределах погранслоя имеется поперечный градиент скорости, то есть действует сила
Слайд 4Из-за возрастания толщины погранслоя уменьшается среднее значение поперечного градиента скорости в
Толщина турбулентного погранслоя нарастает по длине плоской поверхности быстрее, чем толщина ламинарного, так как интенсивность макроскопического переноса импульса в направлении y существенно превосходит интенсивность молекулярного переноса. Вблизи стенки, где абсолютные значения скорости малы, а поперечный градиент скорости велик, сила инерции оказывается малой по сравнению с силой внутреннего трения, а потому ламинарный режим сохраняет устойчивость.
Слайд 5Найдем уравнения, описывающие стационарное движение несжимаемой жидкости в ламинарном погранслое на
В погранслое вектор скорости имеет проекции как на ось х, так и на ось у (см. параллелепипед 1-1-2-2 на слайде 3: расход жидкости, поступающей в параллелепипед через его левую грань, где скорость изменяется от 0 до u0, больше, чем расход жидкости, выходящей из параллелепипеда через правую грань, где скорость изменяется от 0 до величины, меньшей u0; – поскольку жидкость несжимаема, должно быть ее перемещение вдоль оси у).
Действием внешних массовых сил из-за малого объема погранслоя будем пренебрегать.
Слайд 7Оценим порядок входящих в систему величин и отбросим малые величины.
Из-за
Для оценки порядка величины поперечной компоненты скорости используем уравнение неразрывности. Учтем, что порядок n-ой производной равен отношению порядка функции к порядку аргумента в степени n.
, а так как оба слагаемых в левой части уравнения неразрывности должны иметь одинаковый порядок, чтобы в сумме давать 0, тогда , но o(y)=δ, поэтому o(v)=δ.
Слайд 8Из самых общих соображений можно заключить,
Определив порядок величин в уравнениях Навье-Стокса, можно сделать два вывода:
1) в первом уравнении пренебрежимо малой величиной является ;
2) во втором уравнении все оцениваемые величины имеют порядок, не превышающий δ, тогда (считаем, что o(ρ)=1).
Слайд 9Второе уравнение вырождается в условие постоянства давления поперек погранслоя, и получаем
Людвиг Прандтль (1875–1953) – немецкий ученый в области механики. В 1904 году он опубликовал фундаментальную работу – «Течение жидкости с малой вязкостью», в которой впервые описал теорию пограничного слоя и его влияние на лобовое сопротивление и срыв потока, дав объяснение явлению сваливания.
Слайд 10Неизвестными функциями в системе уравнений Прандтля являются u(x,y) и v(x,y). Распределение
.
Но , тогда .
Следовательно, давление в погранслое всюду постоянно.
Слайд 11Уравнения Прандтля для плоской поверхности
Граничные условия для полученных уравнений имеют вид:
при y=0 u=0, v=0;
при у=δ u=u0, .
Слайд 12В стационарном потоке несжимаемой жидкости вблизи плоской поверхности выделим контрольный объем
§ 7. Уравнение потока импульса для пограничного слоя
Слайд 13Определим результирующий поток импульса через поверхность выделенного параллелепипеда, то есть алгебраическую
Через единицу поверхности 1-2 в единицу времени проходит масса ρ⋅u, кг/(м2⋅с), а через элемент поверхности dy⋅1 – масса ρ⋅u⋅dy, кг/c. Умножив эту массу на u, получим поток импульса через элемент поверхности ρ⋅u2⋅dy, кг⋅м/с2.
Поток количества движения через всю поверхность 1-2
.
Слайд 14На расстоянии dx эта величина получит приращение
и поток импульса через грань
.
В связи с тем, что в сечении 3-4 толщина погранслоя больше, чем в сечении 1-2, массовый расход, поступающий в параллелепипед через грань 1-2 (М1-2, кг/c), превышает поток массы, вытекающий через грань 3-4 (М3-4). Таким образом, через грань 2-3 жидкость покидает параллелепипед, и поток импульса через эту грань – отрицателен:
I2-3 = –M2-3 ⋅ u0 .
Слайд 15Так как жидкость несжимаема, то количество жидкости, поступающее в параллелепипед за
Следовательно, с учетом постоянства u0 ,
.
В соответствии с законом сохранения импульса имеем:
I1-2 + I2-3 + I3-4 = dFТР = τW ⋅ dx .
Слайд 16Подставляя выражения для потоков импульса, приводя подобные слагаемые и сокращая на
.
Учитывая, что ρ=const и что в пределах δ≤y≤L интеграл в левой части равенства обращается в нуль, так как в этих пределах u=u0, получим:
– уравнение Кармана.
Это уравнение справедливо как для ламинарного, так и для турбулентного погранслоя, поскольку закон сохранения импульса является общим законом механики.
Слайд 17Для ламинарного погранслоя с учетом формулы Ньютона
уравнение Кармана принимает вид:
Теодор фон Карман (1881–1963) – американский инженер и физик венгерского происхождения, специалист в области воздухоплавания. Работал в Германии и США. Основные труды Кармана связаны с аэродинамическими проблемами авиации и космонавтики.
Слайд 18§ 8. Расчет ламинарного пограничного слоя
на основе интегрального метода
Аппроксимируем поперечный
u(y) = a + b ⋅ y + c ⋅ y2 + d ⋅ y3 ,
где коэффициенты a, b, c и d должно определить из граничных условий для распределения скорости:
1) при y = 0 u = 0 (условие прилипания) ⇒ a = 0;
2) при y = 0 – следствие 1-го уравнения
Прандтля для ламинарного погранслоя, так как на поверхности пластины u = 0 и v = 0 (пластина непроницаема) ⇒ с = 0;
Слайд 193) при y = δ u = u0;
4) при
Третье и четвертое условия дают систему из 2 уравнений с 2 неизвестными, решая которую, найдем:
; .
Подставляя эти результаты в выражение для профиля скорости, получим:
.
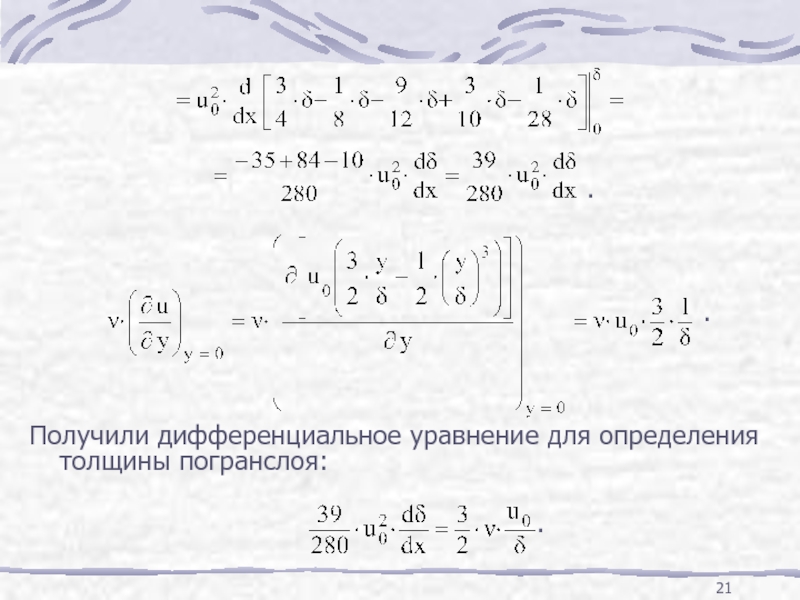
Слайд 20Подставим полученное выражение для u в уравнение Кармана, выполним интегрирование в
Слайд 22Разделим переменные и произведем сокращения:
откуда, интегрируя, находим:
.
При x = 0 δ = 0 ⇒ c = 0. Тогда .
В безразмерной форме:
,
где Rex – число Рейнольдса, в котором роль характерного размера играет расстояние от кромки поверхности.
Слайд 23Формула для δ позволяет найти u(x,y) и v(x,y). Продольная составляющая скорости
Подставим в формулу Ньютона для касательного напряжения трения выражение для поперечного распределения скорости:
.
Подставляя сюда формулу для δ, найдем
.
Слайд 24§ 9. Уравнение Бернулли
Титульный лист «Гидродинамики»
Даниил Бернулли (1700–
Слайд 25Рассмотрим элемент трубки тока, движение в котором происходит в направлении n.
Уравнение Эйлера в проекции на ось n (обозначим проекцию вектора скорости на это направление u и учтем, что в связи со стационарностью движения и малостью поперечного сечения трубки тока скорость и давление зависят только от n):
,
где .
Слайд 26Умножая обе части уравнения на ρ, получим:
Проинтегрируем по n и обозначим ρ⋅g=γ (удельный вес):
,
то есть сумма объемных плотностей кинетической энергии, потенциальной энергии давления и положения (динамического, статического и геометрического давления) не изменяется.
Для потока реальной жидкости в трубе или канале уравнение Бернулли имеет вид:
.
Слайд 27Величину α называют коэффициентом Кориолиса. Она
.
Гаспар-Гюстав де Кориолис (1792–1843) – французский математик, инженер и механик. Его имя внесено в список величайших ученых Франции, помещенный на первом этаже Эйфелевой башни.
pПОТ – потери давления, обусловленные переходом части механической энергии в теплоту.
Слайд 28§ 10. Потери давления на трение
Потери давления на трение представляют собой работу силы трения, отнесенную к единице объема жидкости, и пропорциональны динамическому давлению, рассчитанному по средней скорости:
,
где ξТР – коэффициент сопротивления трения;
λ – гидравлический коэффициент трения;
L – длина исследуемого участка трубы;
– гидравлический диаметр трубы
(S – площадь поперечного сечения, P – периметр).
Слайд 29При ламинарном режиме движения λ~1/Re. Так, для круглой трубы
При турбулентном течении в гидравлически гладкой трубе в соответствии с эмпирической формулой Блазиуса
.
При течении в гидравлически шероховатой трубе λ рассчитывается по формуле Никурадзе:
,
где r0 – радиус трубы,
Δ – высота выступов шероховатости.
Слайд 30Потери давления на местные сопротивления обусловлены, во-первых, изменением величины
,
где ξМС – коэффициент местного сопротивления.
Этот коэффициент определяется экспериментально. Лишь для случая внезапного расширения его можно приближенно найти теоретически.
Слайд 31Считаем, что на всей площади левого сечения контрольного объема давление постоянно
,
так как сила давления, действующая на правое сечение контрольного объема, положительна, поскольку она уменьшает поток импульса.
.
Слайд 32В соответствии с уравнением неразрывности
.
.
Для идеальной жидкости в соответствии с уравнением Бернулли
.
Слайд 33
то есть потеря давления при внезапном расширении равна динамическому давлению потерянной скорости, что составляет содержание так называемой теоремы Борда.
Жан Шарль де Борда (1733–1799) – французский математик, физик, геодезист, политолог и моряк. Его изыскания, напечатанные в «Мемуарах» Парижской академии в 1763 г., 1767 и 1770 гг., привели к заключению, что сопротивление течению жидкостей пропорционально приблизительно квадратам скоростей. Борда занимался также истечением жидкостей из сосудов через малые отверстия, работами над установлением десятичной системы мер и весов.
Слайд 34Подставляя значение , получим:
то есть
,
если расчет ведется по динамическому давлению в узком сечении.
Если же расчет ведется по динамическому давлению в широком сечении, то
.