- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гидродинамика Солнца. (Лекция 6) презентация
Содержание
- 1. Гидродинамика Солнца. (Лекция 6)
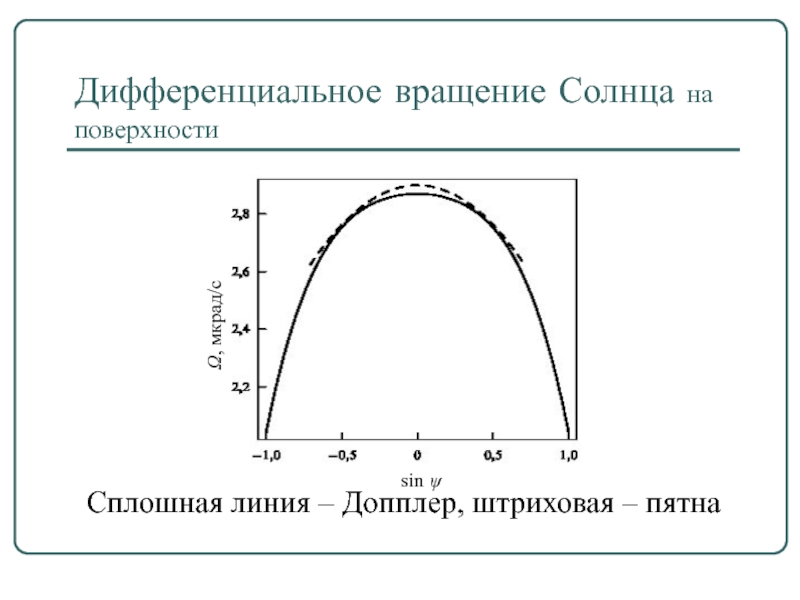
- 2. Дифференциальное вращение Солнца на поверхности По пятнам
- 3. Дифференциальное вращение Солнца на поверхности По Допплеру
- 4. Дифференциальное вращение Солнца на поверхности
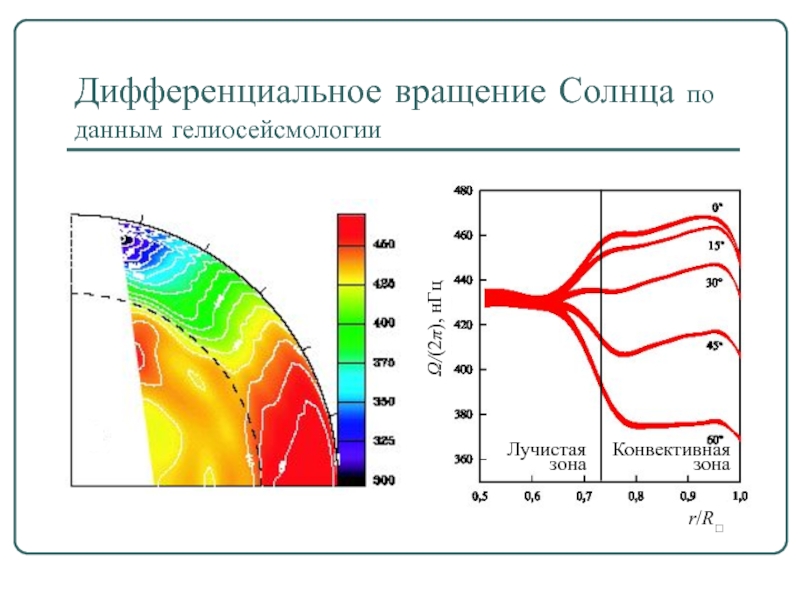
- 5. Дифференциальное вращение Солнца по данным гелиосейсмологии
- 6. Элементы теории дифференциального вращения
- 7. Дифференциальное вращение ― результат взаимодействия конвекции и
- 8. Уравнение Навье – Стокса (тензор вязких напряжений без учета второй вязкости)
- 9. Приближение неупругости (anelastic approximation). Разделение средней и флуктуирующей составляющих поля скоростей
- 10. Усредненное уравнение Навье – Стокса
- 11. Усредненное уравнение Навье – Стокса
- 12. Усредненная скорость в сферических координатах
- 13. Азимутальная компонента усредненного уравнения Навье – Стокса
- 14. Азимутальная компонента усредненного уравнения Навье – Стокса
- 15. Азимутальная компонента усредненного уравнения Навье – Стокса
- 16. Диссипативные и недиссипативные потоки момента импульса
- 17. Установившийся режим вращения Дифференциальное вращение ? баланс
- 18. Меридиональная циркуляция
- 19. Азимутальная компонента ротора уравнения Навье – Стокса для усредненного течения
- 20. Уравнение для меридиональной циркуляции
- 21. Источники меридиональной циркуляции
- 22. Разрешение загадки числа Тейлора Распределение угловой скорости
- 23. Наблюдения меридиональной циркуляции Допплеровские измерения на поверхности:
- 24. Происхождение бароклинного источника меридиональной циркуляции Анизотропия турбулентной
- 25. Вычисление напряжений Рейнольдса
- 26. Вычисление напряжений Рейнольдса Интенсивность исходной турбулентности (в невращающейся среде) рассчитывается по теории пути перемешивания:
- 27. Происхождение Λ-эффекта uruφ > 0
- 28. Происхождение Λ-эффекта uruφ > 0
- 29. Источники Λ-эффекта Анизотропия турбулентности Неоднородность турбулентной среды
- 30. Заключительный этап построения модели Расчет эффективных вязкостей и температуропроводностей для вращающейся турбулентной среды
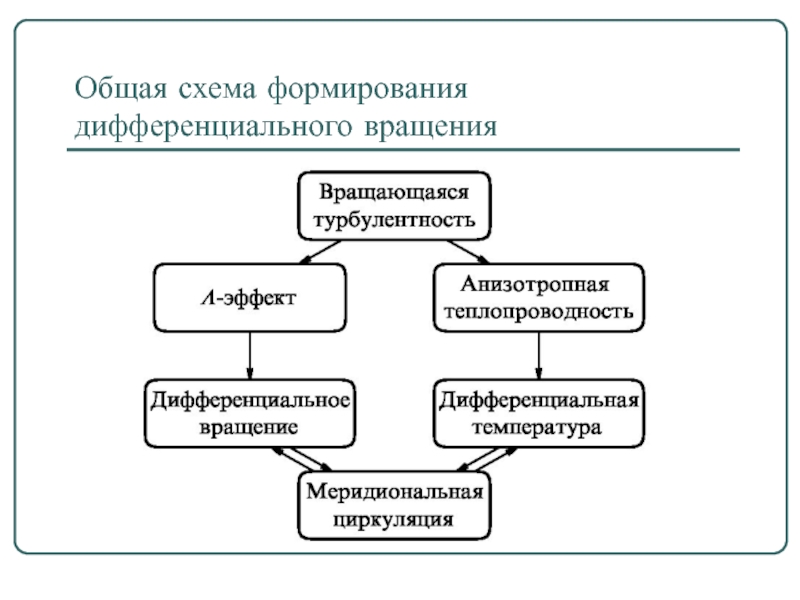
- 31. Общая схема формирования дифференциального вращения
- 32. Трудности ранних моделей – Чисто гидродинамические модели:
- 33. Современные модели Единственный свободный параметр – коэффициент
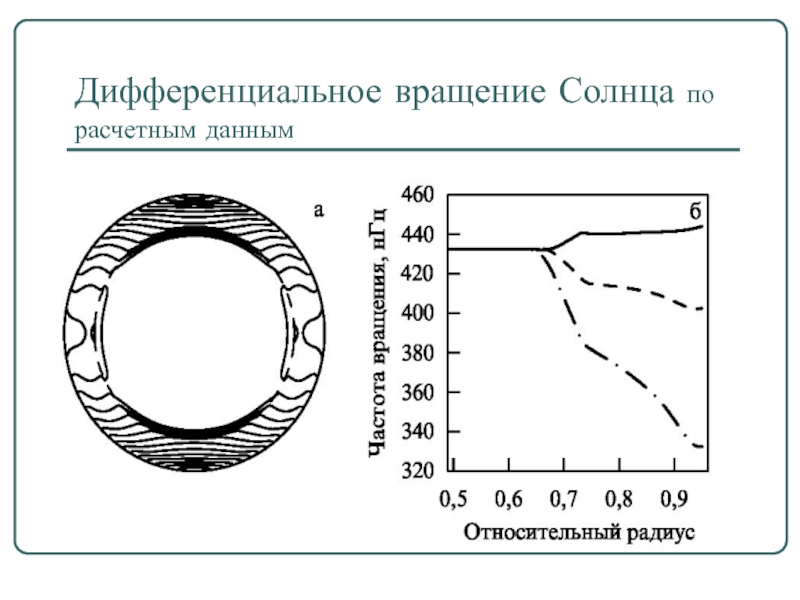
- 34. Дифференциальное вращение Солнца по расчетным данным
- 35. Дифференциальное вращение Солнца по данным гелиосейсмологии
- 36. Литература Л.Л. Кичатинов. Дифференциальное вращение звезд. УФН, 175 (5), 457–476, 2005.
Дифференциальное вращение Солнца на поверхности По пятнам (Newton & Nunn, 1951): θ = π/2 – ψ ― коширота (полярный угол), Ω0 = 2.90 × 10– 6 ― угловая скорость
Слайд 2Дифференциальное вращение Солнца на поверхности
По пятнам (Newton & Nunn, 1951):
θ =
π/2 – ψ ― коширота (полярный угол),
Ω0 = 2.90 × 10– 6 ― угловая скорость на экваторе,
b = 0.19
Ω0 = 2.90 × 10– 6 ― угловая скорость на экваторе,
b = 0.19
Слайд 3Дифференциальное вращение Солнца на поверхности
По Допплеру (Howard et al., 1983):
θ =
π/2 – ψ ― коширота (полярный угол),
Ω0 = 2.87 × 10– 6 ― угловая скорость на экваторе,
b = 0.12,
c = 0.17
Ω0 = 2.87 × 10– 6 ― угловая скорость на экваторе,
b = 0.12,
c = 0.17
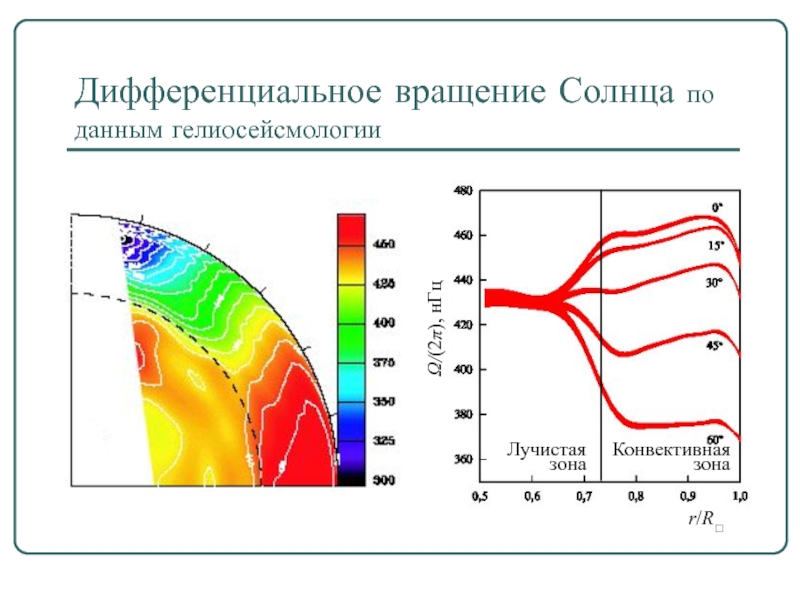
Слайд 5Дифференциальное вращение Солнца по данным гелиосейсмологии
r/R?
Лучистая зона
Конвективная зона
Ω/(2π), нГц
r/R?
Слайд 7Дифференциальное вращение ― результат взаимодействия конвекции и вращения
А. И. Лебединский (1941):
сила Кориолиса воздействует на конвективную турбулентность; в свою очередь, турбулентность возмущает вращение и делает его неоднородным
Слайд 9Приближение неупругости (anelastic approximation).
Разделение средней и флуктуирующей составляющих поля скоростей
Слайд 16Диссипативные и недиссипативные потоки момента импульса
Основная причина неоднородности вращения ― Λ-эффект:
присутствие ненулевого турбулентного потока момента импульса в однородно вращающейся среде (А. И. Лебединский, 1941)
Такой поток может возникать при ненулевых значениях Qφr и Qφθ
Такой поток может возникать при ненулевых значениях Qφr и Qφθ
Слайд 17Установившийся режим вращения
Дифференциальное вращение ? баланс между недиссипативным потоком момента импульса
и потоком, обусловленным турбулентной вязкостью (eddy viscosity); при таком балансе дивергенция полного потока = 0 (вектор потока соленоидален, хотя сам поток может быть и ненулевым)
Слайд 22Разрешение загадки числа Тейлора
Распределение угловой скорости определяется балансом между центробежным и
бароклинным источником меридионального течения (балансом Тейлора – Праудмана)
(меридиональное течение – малым отклонением от этого баланса ? плохая обусловленность обратной задачи нахождения меридионального течения по распределениям Ω и Т)
Слайд 23Наблюдения меридиональной циркуляции
Допплеровские измерения на поверхности: течение от экватора к полюсу
с максимальной скоростью ~ 10 м/с
(гелиосейсмология: это течение прослежено до глубин ~ 12 Мм)
+
Нестационарное течение с меньшими скоростями, сходящееся к широте с максимальной частотой пятнообразования (широта меняется с циклом активности)
(гелиосейсмология: это течение прослежено до глубин ~ 12 Мм)
+
Нестационарное течение с меньшими скоростями, сходящееся к широте с максимальной частотой пятнообразования (широта меняется с циклом активности)
Слайд 24Происхождение бароклинного источника меридиональной циркуляции
Анизотропия турбулентной температуропроводности (χ║
> χ⊥) ? полюса чуть теплее экватора. Для разрешения «загадки числа Тейлора» требуется, чтобы два источника циркуляции (действующие противоположно друг другу) были одного порядка. Нужна разность температур ~ 1 К.
(Ω* – безразмерная угловая скорость)
Слайд 26Вычисление напряжений Рейнольдса
Интенсивность исходной турбулентности (в невращающейся
среде) рассчитывается по теории пути
перемешивания:
Слайд 29Источники Λ-эффекта
Анизотропия турбулентности
Неоднородность турбулентной среды [дает основной вклад уже для τ
≈ 6 (среднее значение по конвективной зоне Солнца) и является определяющей при τ >> 1]
Стратификация конвективных зон близка к изэнтропической! ? модели не содержат свободных параметров
Стратификация конвективных зон близка к изэнтропической! ? модели не содержат свободных параметров
Слайд 30Заключительный этап построения модели
Расчет эффективных вязкостей и температуропроводностей для вращающейся турбулентной
среды
Слайд 32Трудности ранних моделей
– Чисто гидродинамические модели:
дифференциальное вращение меньше наблюдаемого
цилиндрическая симметрия Ω
меридиональная
циркуляция от полюсов к экватору
– «Чисто» термодинамические модели:
требуется слишком большая дифференциальная температура (противоречащая наблюдениям)
меридиональная циркуляция от полюсов к экватору
– Большое количество свободных параметров
– «Чисто» термодинамические модели:
требуется слишком большая дифференциальная температура (противоречащая наблюдениям)
меридиональная циркуляция от полюсов к экватору
– Большое количество свободных параметров
Слайд 33Современные модели
Единственный свободный параметр – коэффициент α:
l = αHP
Наилучшие результаты –
при 1.5 < α < 2
Слайд 35Дифференциальное вращение Солнца по данным гелиосейсмологии
r/R?
Лучистая зона
Конвективная зона
Ω/(2π), нГц
r/R?
