Кафедра физики, математики и информатики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гидродинамика и гемодинамика презентация
Содержание
- 1. Гидродинамика и гемодинамика
- 2. 1.Уравнение неразрывности потока жидкости. Уравнение Бернулли. Статическое
- 3. Вопросы (продолжение) 6. Кровь как жидкость. Особенности
- 4. 1. Уравнение неразрывности потока
- 5. Уравнение Бернулли P1,P2 – статическое
- 6. Уравнение Бернулли P + ρgH +
- 7. Как работает уравнение Бернулли
- 8. Важное следствие из уравнения
- 9. Некоторые важные понятия гидродинамики 1. Линия
- 10. 2. Вязкость жидкости Вязкость – или
- 11. Коэффициент вязкости. Из формулы (3) следует, что
- 12. Другие коэффициенты вязкости В физике
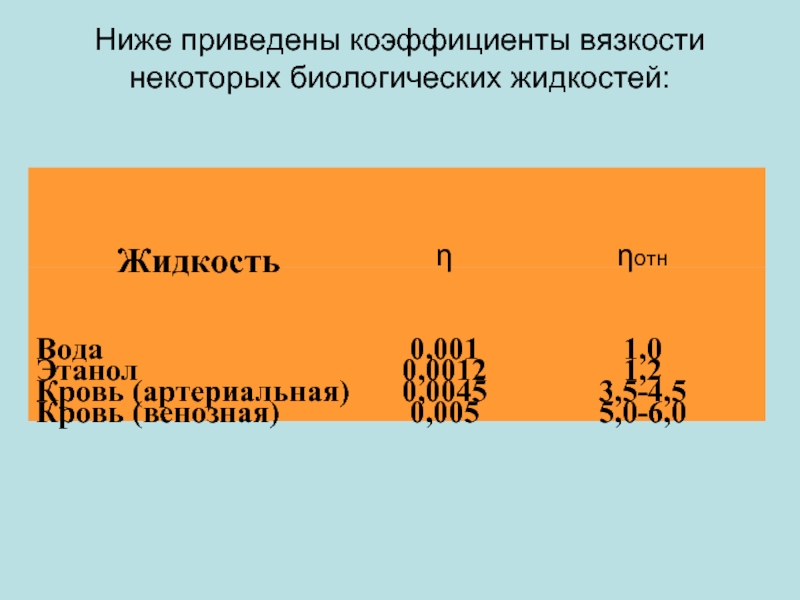
- 13. Ниже приведены коэффициенты вязкости некоторых биологических жидкостей:
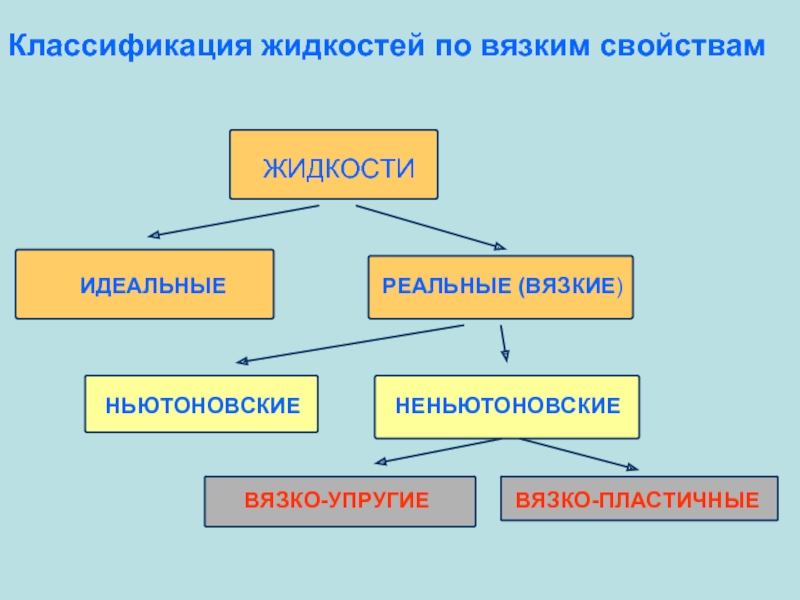
- 14. Классификация жидкостей по вязким свойствам
- 15. Классификация жидкостей по вязким свойствам
- 16. У неньютоновских жидкостей коэффициент вязкости зависит градиента
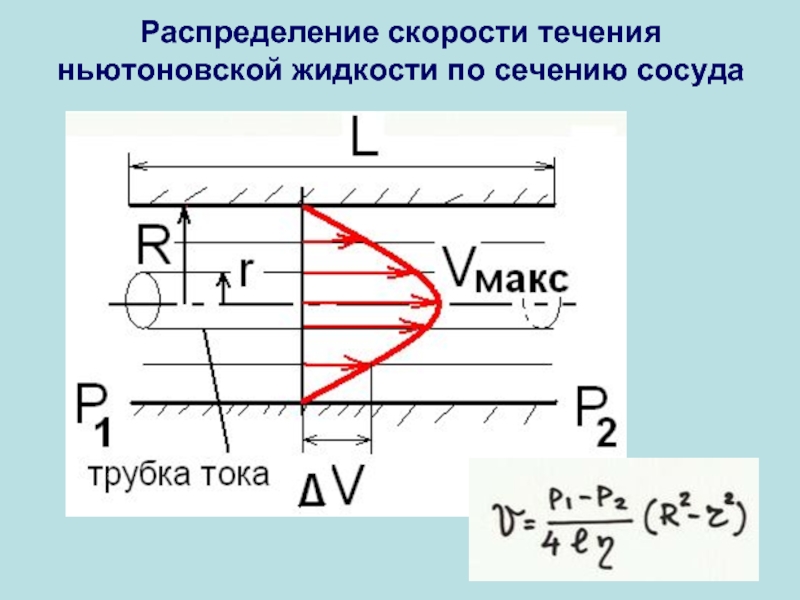
- 17. Распределение скорости течения ньютоновской жидкости по сечению сосуда
- 18. Где: Q – объемная скорость потока
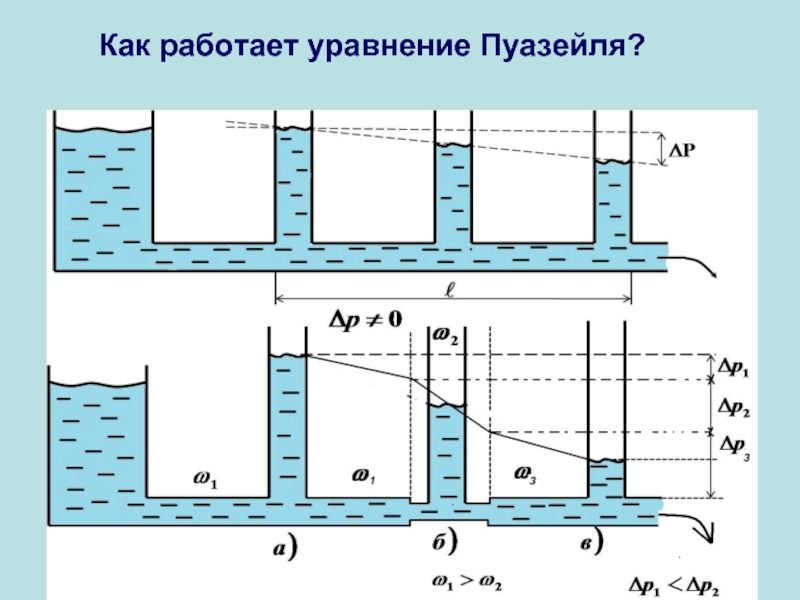
- 19. Как работает уравнение Пуазейля?
- 20. 4. Гидравлическое сопротивление Оставим в числителе
- 21. Омическое сопротивление и гидравлическое похожи
- 22. Гидравлическое сопротивление Посмотрим на эти формулы внимательнее:
- 23. Гидравлическое сопротивление При разветвлении гидравлической системы
- 24. 5. Характер течения жидкости по
- 25. Характер течения жидкости по сосудам 2.
- 26. Характер течения жидкости определяется критерием Рейнольдса (безразмерная
- 27. Два важных вывода из вышеизложенного У клапанов
- 28. Гемодинамика – раздел биофизики, изучающий текучесть
- 29. Т.к. у стенок скорость крови меньше, чем
- 30. Размеры эритроцитов ≈ равны диаметру капилляров.
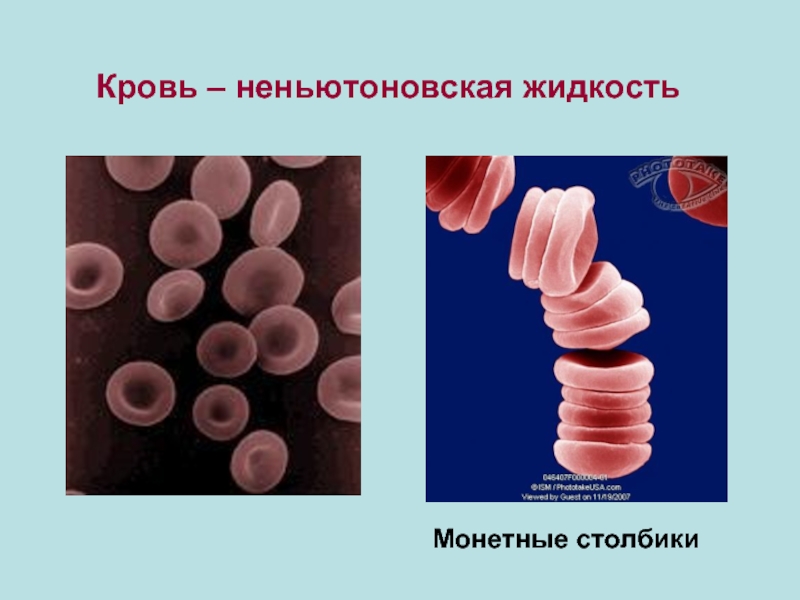
- 31. Кровь – неньютоновская жидкость Монетные столбики
- 32. Влияние эластичности стенок сосудов Вторая особенность
- 33. Гидравлическая модель сердечно-сосудистой системы Начальное давление,
- 34. 7. Давление и скорость кровотока
- 35. Давление и скорость кровотока Давление
- 36. Давление и скорость кровотока Давление
- 37. 8. Пульсовая волна Волна давления,
- 38. 9. Работа сердца Работа при однократном
- 39. 10. Резистивная модель сердца Мы
Слайд 1Тема:
«Гидродинамика и гемодинамика»
ГОУ ВПО Ивановская Государственная медицинская академия агентства по
Слайд 21.Уравнение неразрывности потока жидкости. Уравнение Бернулли. Статическое и динамическое давление в
Вопросы
Слайд 3Вопросы (продолжение)
6. Кровь как жидкость. Особенности протекания крови по сосудам.
7.
Слайд 4
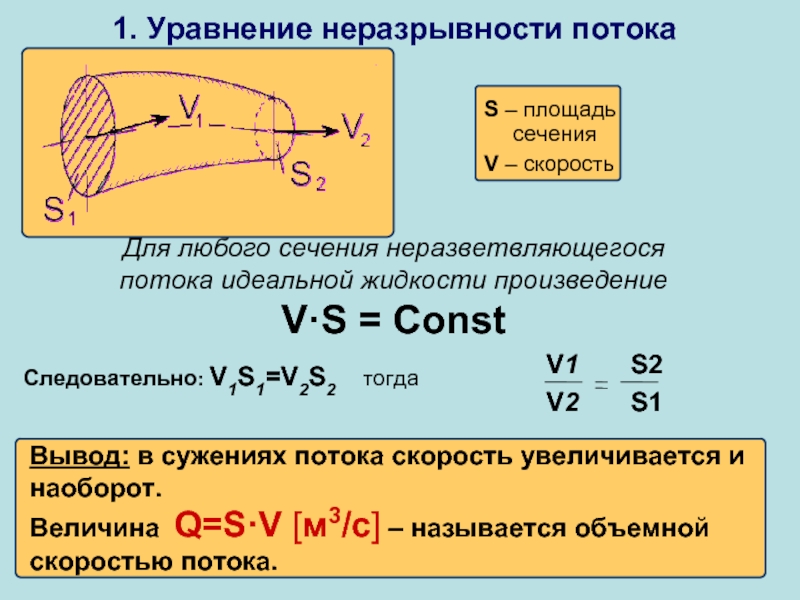
1. Уравнение неразрывности потока
S – площадь сечения
V – скорость
Для любого сечения
Следовательно: V1S1=V2S2 тогда
Вывод: в сужениях потока скорость увеличивается и наоборот.
Величина Q=S·V [м3/с] – называется объемной скоростью потока.
Слайд 5
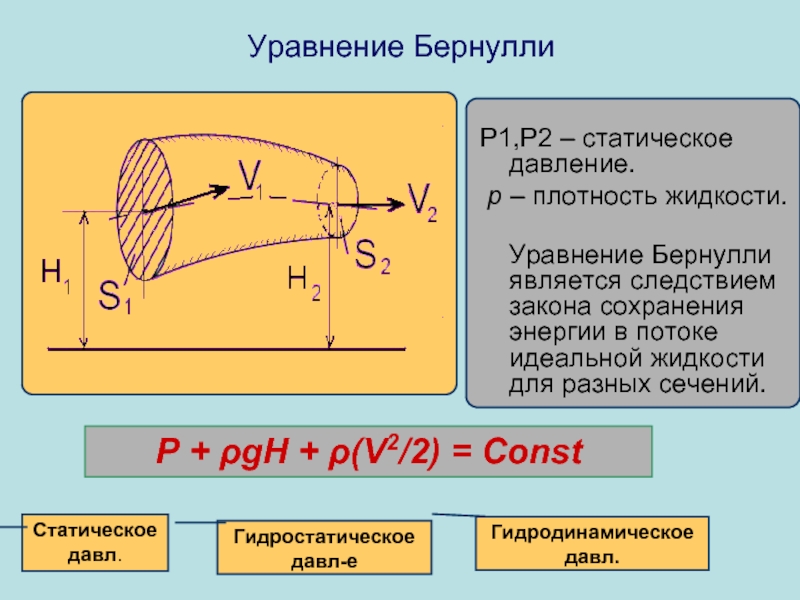
Уравнение Бернулли
P1,P2 – статическое давление.
p – плотность жидкости.
Уравнение Бернулли является
P + ρgH + ρ(V2/2) = Const
Гидростатическое давл-е
Статическое давл.
Гидродинамическое давл.
Слайд 8
Важное следствие из уравнения
Бернулли для горизонтальной
трубы: h1=h2, следовательно уравнение
(2)
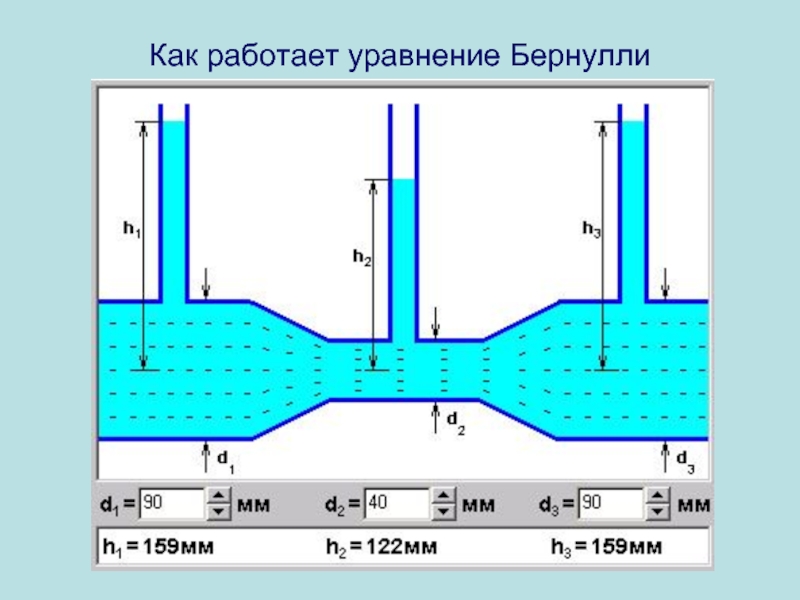
ВЫВОД: так как в узких местах труб скорость увеличивается, то по уравнению (2) статическое давление должно уменьшаться.
На рисунке вверху показано, что в узком месте уровень манометрической трубки ниже , чем в более широких частях.
(1)
Слайд 9
Некоторые важные понятия гидродинамики
1. Линия тока – линия, проведенная в потоке
2. Стационарное течение – характер течения, когда вектор скорости в каждой точке остается постоянным. Картина линий тока в СТ не изменяется, а линии тока совпадают с траекториями частиц.
3. Трубка тока – часть жидкости ограниченная линиями тока. Т. к. вектор скорости касателен к линиям тока, то он касателен и к трубке тока, т. е. частицы жидкости не пересекают границ трубки тока.
Линия
тока
Трубка тока
Слайд 10
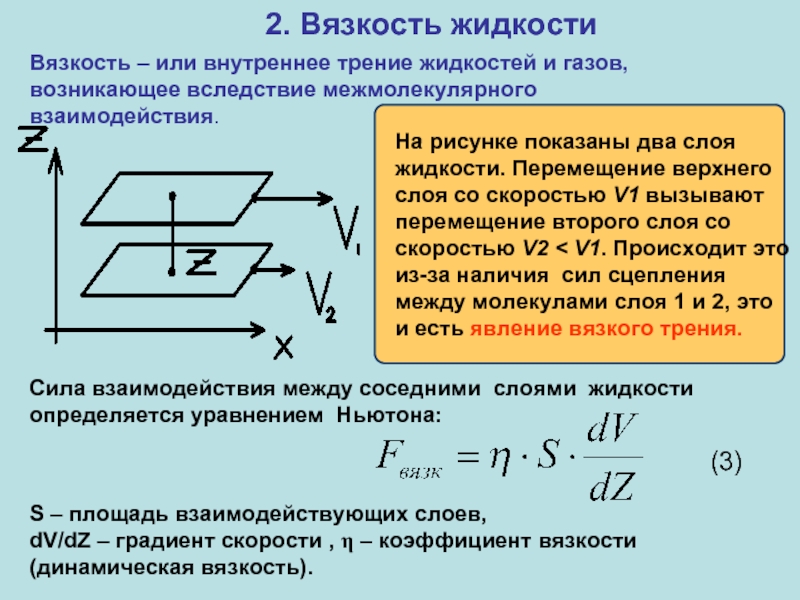
2. Вязкость жидкости
Вязкость – или внутреннее трение жидкостей и газов, возникающее
На рисунке показаны два слоя жидкости. Перемещение верхнего слоя со скоростью V1 вызывают перемещение второго слоя со скоростью V2 < V1. Происходит это из-за наличия сил сцепления между молекулами слоя 1 и 2, это и есть явление вязкого трения.
Сила взаимодействия между соседними слоями жидкости определяется уравнением Ньютона:
(3)
S – площадь взаимодействующих слоев,
dV/dZ – градиент скорости , η – коэффициент вязкости (динамическая вязкость).
Слайд 11Коэффициент вязкости.
Из формулы (3) следует, что коэффициент вязкости
Это основной параметр, характеризующий
Слайд 12
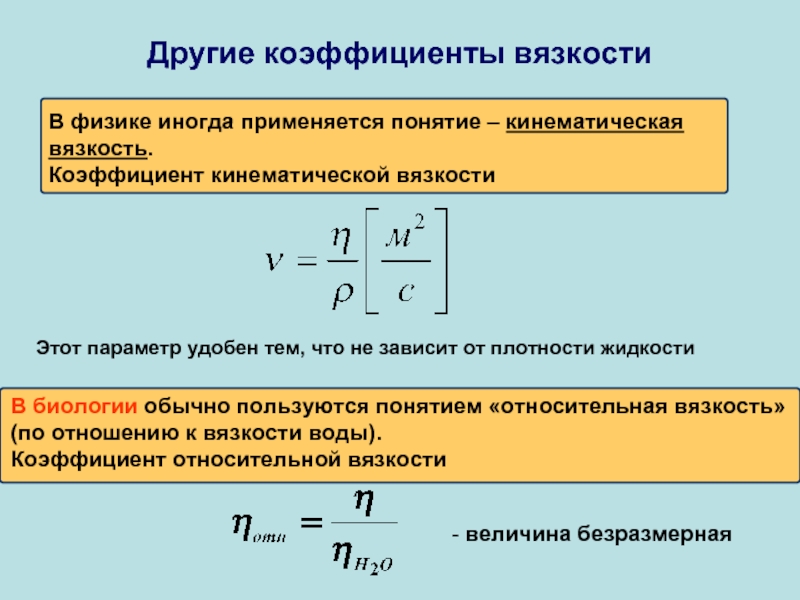
Другие коэффициенты вязкости
В физике иногда применяется понятие – кинематическая вязкость.
Коэффициент кинематической
Этот параметр удобен тем, что не зависит от плотности жидкости
В биологии обычно пользуются понятием «относительная вязкость» (по отношению к вязкости воды).
Коэффициент относительной вязкости
- величина безразмерная
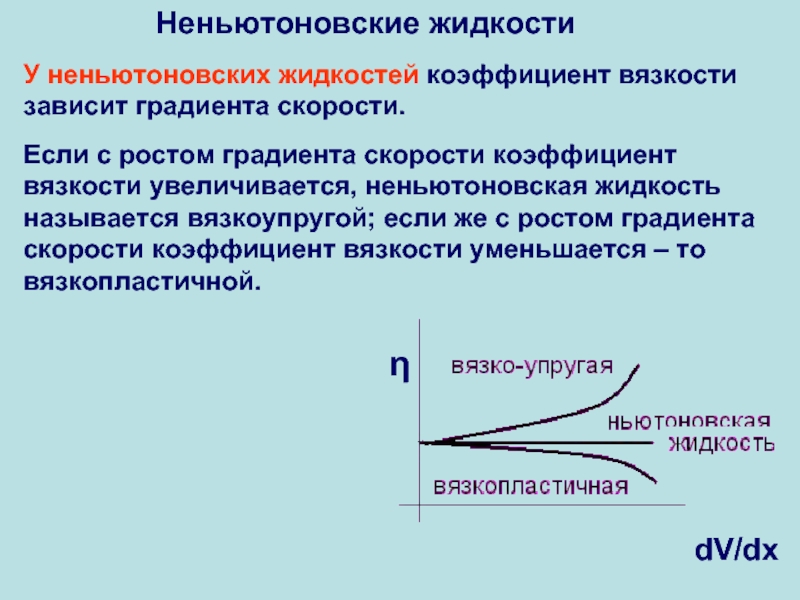
Слайд 16У неньютоновских жидкостей коэффициент вязкости зависит градиента скорости.
Если с ростом
Неньютоновские жидкости
η
dV/dx
Слайд 18
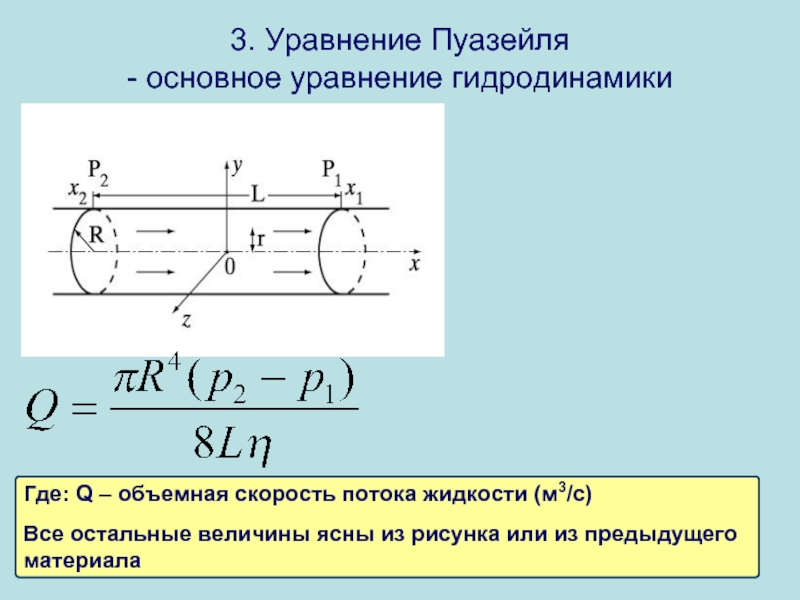
Где: Q – объемная скорость потока жидкости (м3/с)
Все остальные величины ясны
3. Уравнение Пуазейля
- основное уравнение гидродинамики
Слайд 204. Гидравлическое сопротивление
Оставим в числителе только Δр остальное вынесем в знаменатель:
ω
Слайд 21
Омическое сопротивление и гидравлическое похожи по смыслу.
Омическое сопротивление пропорционально длине проводника,
Гидравлическое сопротивление пропорционально длине участка трубы, обратно пропорционально радиусу трубы в четвертой степени и зависит от свойств жидкости (вязкости) .
Гидравлическое сопротивление
I = U / R – закон Ома для участка электрической цепи
Q = Δp/ω – закон Пуазейля для участка гидравлической цепи
При последовательном соединении любых видов сопротивлений, общее сопротивление увеличивается. При параллельном соединении – уменьшается.
Слайд 22Гидравлическое сопротивление
Посмотрим на эти формулы внимательнее:
У гидравлического сопротивления зависимость от радиуса
Слайд 23
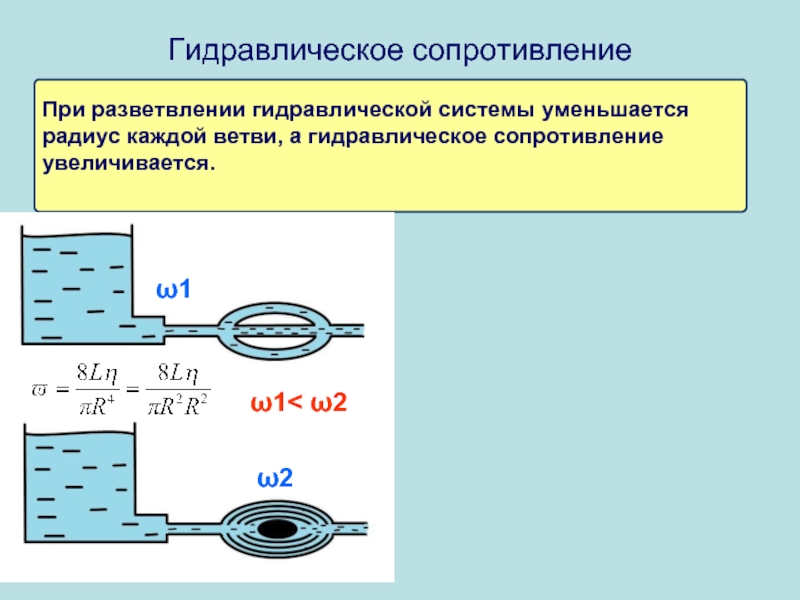
Гидравлическое сопротивление
При разветвлении гидравлической системы уменьшается радиус каждой ветви, а гидравлическое
ω1< ω2
ω1
ω2
Слайд 24
5. Характер течения жидкости по сосудам
1. Ламинарное (спокойное) течение – это
В норме течение крови по сосудам имеет ламинарный характер
Такой характер течение жидкости имеется при относительно небольших скоростях в трубах с гладкими стенками при отсутствии множественных разветвлений.
Слайд 25
Характер течения жидкости по сосудам
2. Турбулентное течение. Это вихревое течение, в
Слайд 26Характер течения жидкости определяется критерием Рейнольдса (безразмерная величина):
Переход от ламинарного течения
ЧИСЛО РЕЙНОЛЬДСА
где: η - коэффициент динамической вязкости,
ρ – плотность жидкости,
D – диаметр сосуда,
Re – число Рейнольдса
Слайд 27Два важных вывода из вышеизложенного
У клапанов сердца поток крови турбулентный, завихрения
Исследование шумов сердца является областью диагностики ССС, получившей название – фонокардиография. Есть и другие применения звуковых методов исследования потоков крови.
Слайд 28
Гемодинамика – раздел биофизики, изучающий текучесть и деформацию крови в сосудистой
Кровь состоит из плазмы и форменных элементов (эритроциты -93%, лейкоциты и тромбоциты – 7%) – неньютоновская (вязкопластичная) жидкость.
Плазма – коллоидная суспензия белков в электролите из ионов неорганических и органических кислот- ньютоновская жидкость.
В норме вязкость крови: в аорте ≈ 3,5, плазмы – 2 ед.
6. Элементы гемодинамики
На вязкость крови сильно влияет объемная концентрация эритроцитов в плазме – т.н. гематокрит (Г).
Г=Vэритроцитов / Vплазмы.
Норма Г = 0,4.. С увеличением гематокрита (доли эритроцитов), увеличивается вязкость крови.
Слайд 29Т.к. у стенок скорость крови меньше, чем в центре, а по
Элементы гемодинамики
Слайд 30
Размеры эритроцитов ≈ равны диаметру капилляров. Эритроцит в капилляре деформируется, но
Элементы гемодинамики
В венах увеличивается концентрация СО2 в крови. Объем эритроцитов увеличивается, соответственно увеличивается вязкость крови.
Примерная схема движения крови по капиллярам приведена на рисунке, однако механизм движения эритроцитов по капиллярам математически описать весьма сложно
Слайд 32
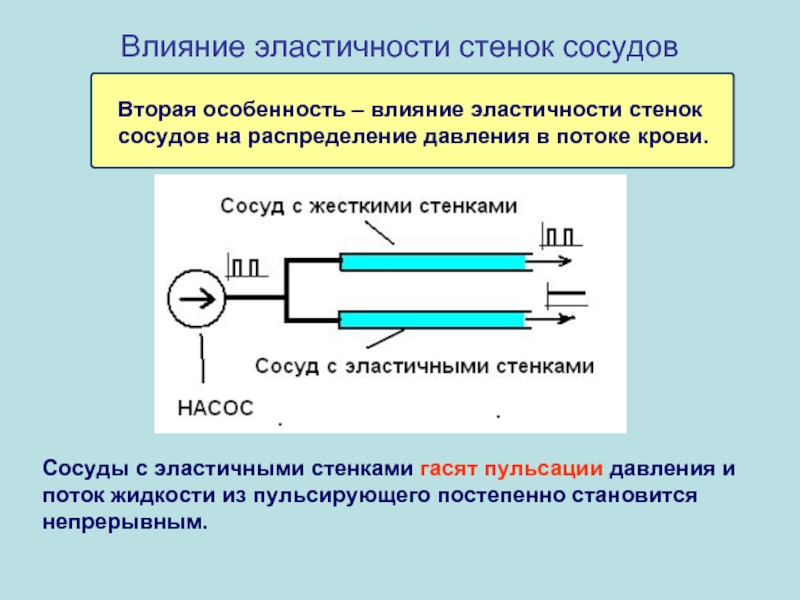
Влияние эластичности стенок сосудов
Вторая особенность – влияние эластичности стенок сосудов на
Сосуды с эластичными стенками гасят пульсации давления и поток жидкости из пульсирующего постепенно становится непрерывным.
Слайд 33
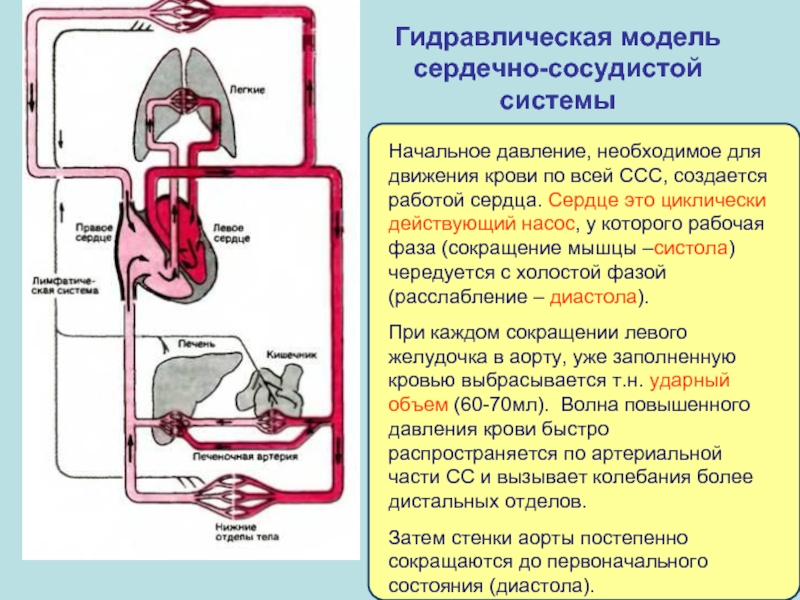
Гидравлическая модель сердечно-сосудистой системы
Начальное давление, необходимое для движения крови по всей
При каждом сокращении левого желудочка в аорту, уже заполненную кровью выбрасывается т.н. ударный объем (60-70мл). Волна повышенного давления крови быстро распространяется по артериальной части СС и вызывает колебания более дистальных отделов.
Затем стенки аорты постепенно сокращаются до первоначального состояния (диастола).
Слайд 35
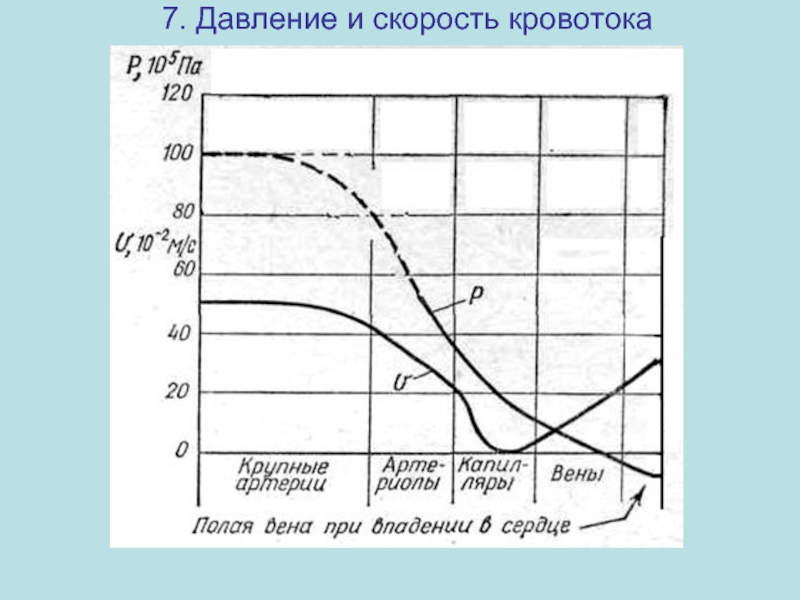
Давление и скорость кровотока
Давление в кровеносной системе максимально а аорте, затем
Например, наибольшее падение давления, не менее чем на 50% начальногопроисходит в артериолах. Число артериол в сотни раз больше, чем крупных артерий при сравнительно небольшом увеличении суммарного поперечного сечения. Поэтому потери давления здесь весьма велики.
Общее число капилляров еще больше, однако длина их настолько мала. Что падение давления в них велико, но меньше, чем в артериолах.
Слайд 36
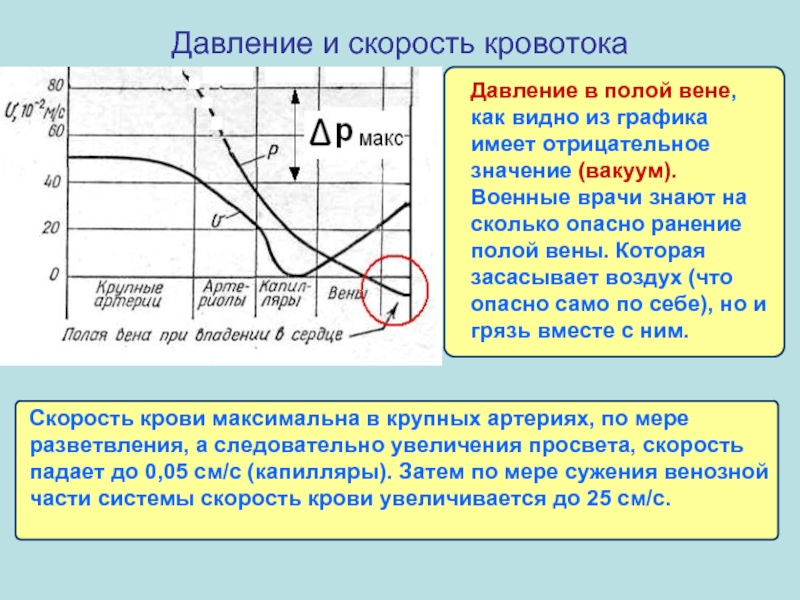
Давление и скорость кровотока
Давление в полой вене, как видно из графика
Скорость крови максимальна в крупных артериях, по мере разветвления, а следовательно увеличения просвета, скорость падает до 0,05 см/с (капилляры). Затем по мере сужения венозной части системы скорость крови увеличивается до 25 см/с.
Слайд 37
8. Пульсовая волна
Волна давления, распространяющаяся по сосудам ССС носит название пульсовой
За время систолы (0,3с) пульсовая волна достигает конечностей, т.е. раньше, чем начнется спад давления в аорте.
Скорость пульсовой волны в крупных сосудах определяется формулой Моенса-Кортивега:
Где: Е – модуль упругости стенки сосуда
h - толщина стенки
ρ – плотность ткани сосуда
d – диаметр сосуда
Слайд 38
9. Работа сердца
Работа при однократном сокращении левого желудочка:
Ал = рVуд +
Работа левого и правого желудочнов:
А = Ал + 0,2Ал = 1,2 (рVуд + ρVуд v2/2)
р = 13 кПа, Vуд = 60 мл. ρ = 1,05 ·103 кг/м3 тогда А = 1 дж – работа разового сокращения в состоянии покоя.
Средняя мощность за одно сокращение (время систолы 0,3с) W = Ф/tc = 3.3 вт.
При нагрузках работа сердца может увеличиться в несколько раз
Слайд 39
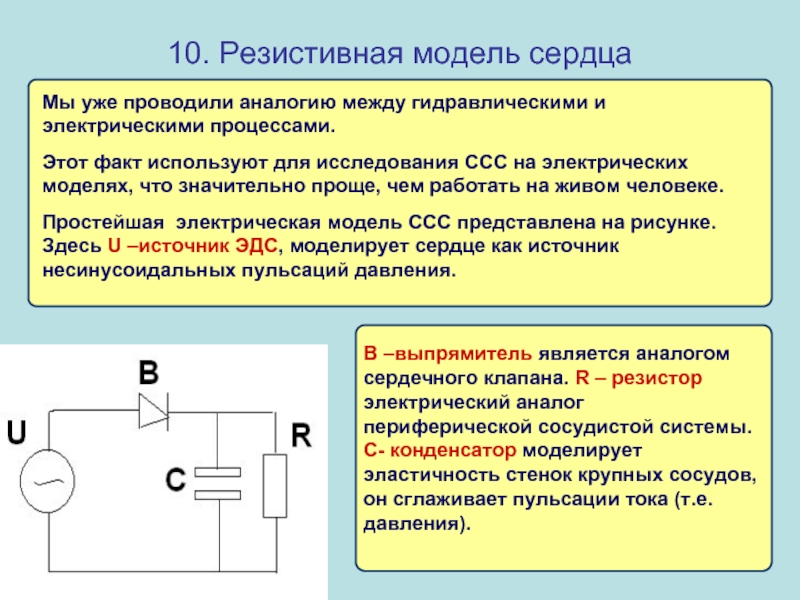
10. Резистивная модель сердца
Мы уже проводили аналогию между гидравлическими и электрическими
Этот факт используют для исследования ССС на электрических моделях, что значительно проще, чем работать на живом человеке.
Простейшая электрическая модель ССС представлена на рисунке. Здесь U –источник ЭДС, моделирует сердце как источник несинусоидальных пульсаций давления.
В –выпрямитель является аналогом сердечного клапана. R – резистор электрический аналог периферической сосудистой системы. С- конденсатор моделирует эластичность стенок крупных сосудов, он сглаживает пульсации тока (т.е. давления).