- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
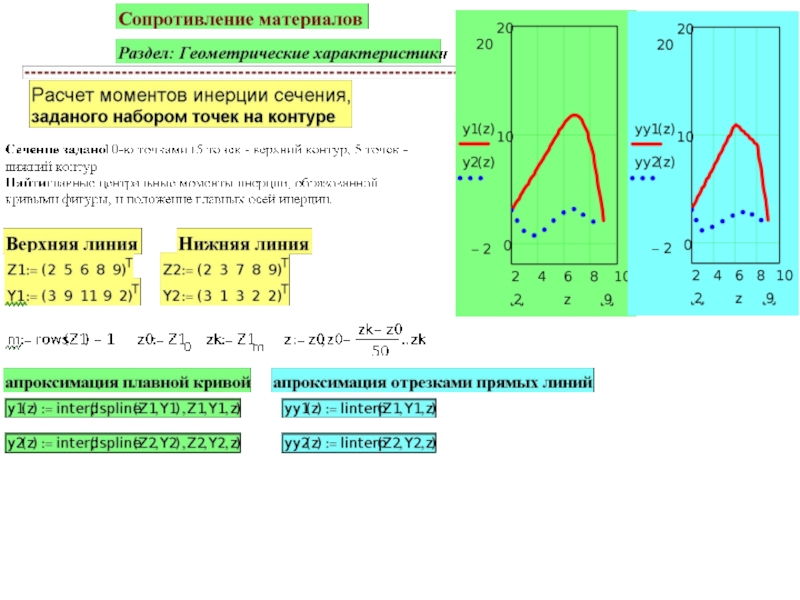
Геометрические характеристики плоских сечений презентация
Содержание
- 1. Геометрические характеристики плоских сечений
- 2. 1. Понятие о моментах сечения Статические моменты
- 3. Моменты Jz, Jy, Jp всегда положительны и
- 4. 2. Понятие о центре тяжести сечения и
- 5. Приравниваем первые и последние выражения и выражаем
- 6. 3. Зависимости между моментами инерции относительно параллельных
- 7. Аналогично Следовательно Центробежный момент инерции сечения относительно
- 8. 4. Зависимости между моментами инерции относительно осей,
- 9. Для практического применения формулы иногда преобразовывают в вид: И то же самое для центробежного момента
- 10. 5. Главные оси и главные моменты инерции
- 11. Так как по определению главных осей центробежный
- 12. Проведя преобразования можно получить, что Для того
- 13. Радиусом инерции сечения относительно некоторой оси, например
- 14. 6. Свойства моментов инерции геометрических фигур Свойство
- 15. Свойство моментов инерции правильных фигур относительно центральных
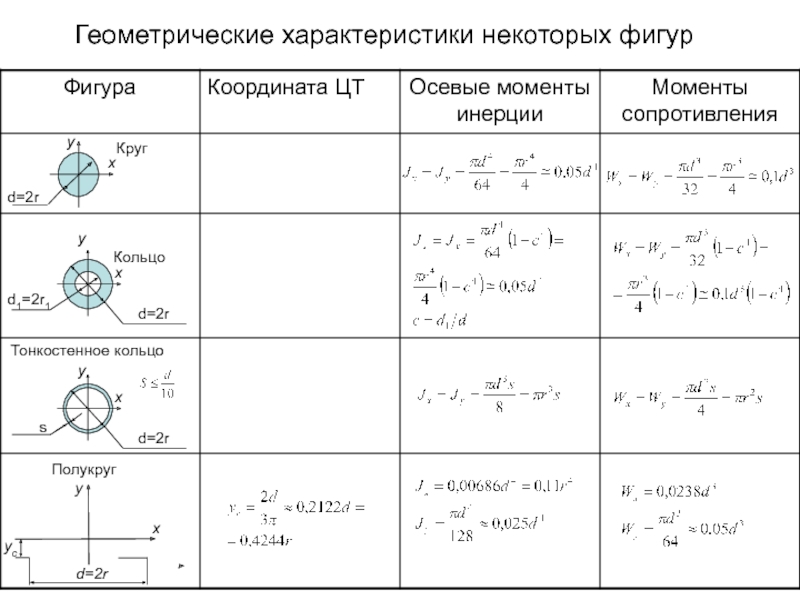
- 16. Геометрические характеристики некоторых фигур y d=2r yc y x Полукруг
- 17. x y Тонкостенный квадрат s
Слайд 1Геометрические характеристики плоских сечений
Доцент кафедры самолетостроения
К.т.н Мухин Д.В.
Слайд 21. Понятие о моментах сечения
Статические моменты сечения относительно осей z и
Осевые моменты инерции сечения относительно осей z и y
Центробежный моменты инерции сечения относительно осей z и y
Полярный моменты инерции сечения относительно начала координат
Так как все моменты сечений по сути являются интегралами по площади, то на них распространяются свойства этого вида интегралов. В частности если сечение состоит из нескольких частей, что общий момент (любого вида) всего сечения будет равен сумме моментов отдельных его частей.
Слайд 3Моменты Jz, Jy, Jp всегда положительны и никогда не равняются нулю,
Зависимость между осевыми и полярными моментами инерции можно получить, если подставить в выражение Jp равенство
тогда
Полярный момент инерции сечения относительно точки равен сумме его моментов инерции относительно любых взаимно перпендикулярных осей, проходящих через эту точку.
Следствие. Сумма осевых моментов инерции сечения относительно любых взаимно перпендикулярных осей, проходящих через данную точку, есть величина постоянная:
Слайд 42. Понятие о центре тяжести сечения и свойство статическою момента
Центром тяжести
Если положение центра тяжести сечения известно, то
Статический момент сечения относительно оси равняется его площади, умноженной на расстояние от центра тяжести сечения до этой оси.
Если ось y проходит через центр тяжести сечения, то
Статический момент сечения относительно оси, проходящей через его центр тяжести (относительно центральной оси), равен нулю
Слайд 5Приравниваем первые и последние выражения и выражаем из них координаты центра
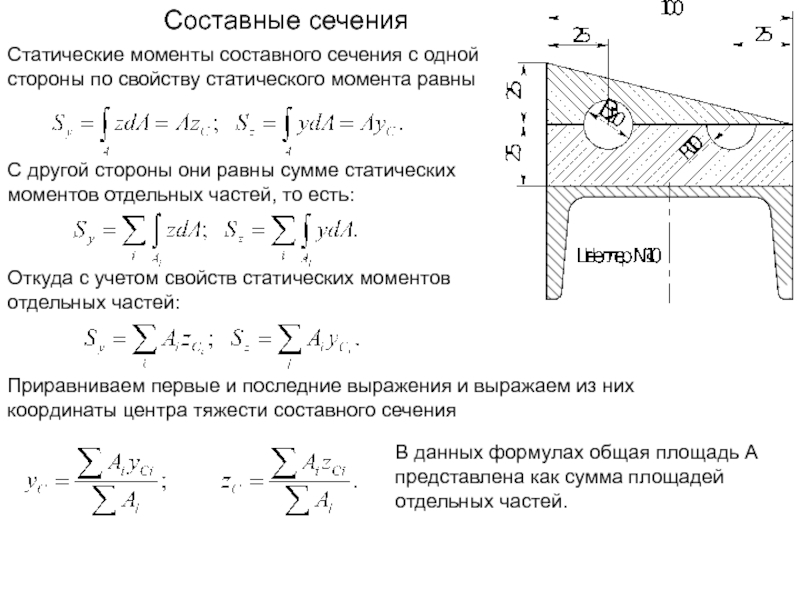
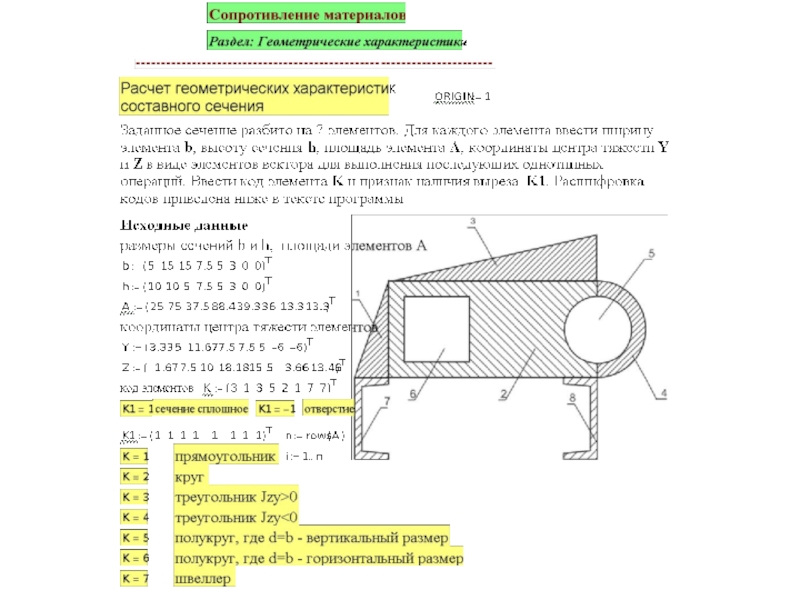
Составные сечения
Статические моменты составного сечения с одной стороны по свойству статического момента равны
С другой стороны они равны сумме статических моментов отдельных частей, то есть:
Откуда с учетом свойств статических моментов отдельных частей:
В данных формулах общая площадь А представлена как сумма площадей отдельных частей.
Слайд 63. Зависимости между моментами инерции относительно параллельных осей (формулы параллельного переноса)
Из
Откуда
Момент инерции сечения относительно оси равен его моменту инерции относительно центральной оси, параллельной ей, сложенному с произведением квадрата расстояния между осями на площадь сечении.
Аналогично
Слайд 7Аналогично
Следовательно
Центробежный момент инерции сечения относительно перпендикулярных осей равняется центробежному моменту инерции
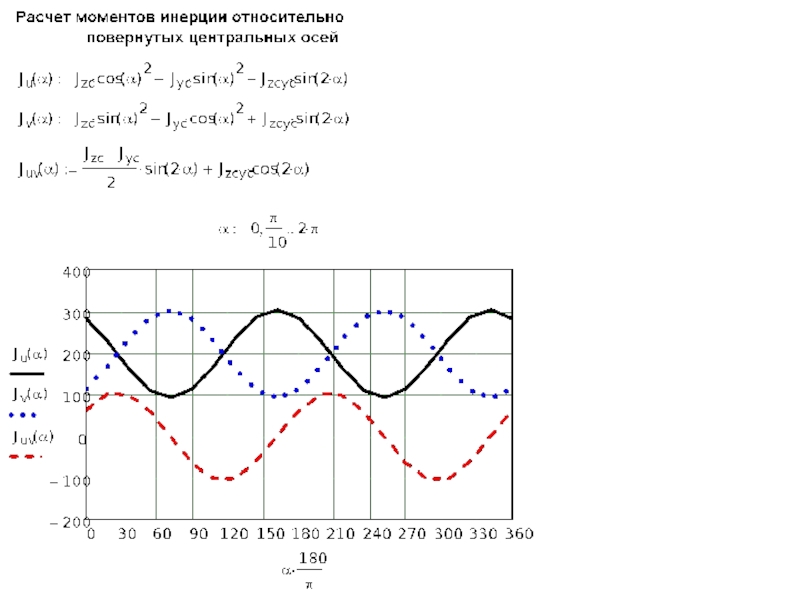
Слайд 84. Зависимости между моментами инерции относительно осей, проходящих через данную точку
z
Из
в которых угол α отсчитывается от оси z в направлении против часовой стрелки.
По определению
По аналогии
Слайд 9Для практического применения формулы иногда преобразовывают в вид:
И то же самое
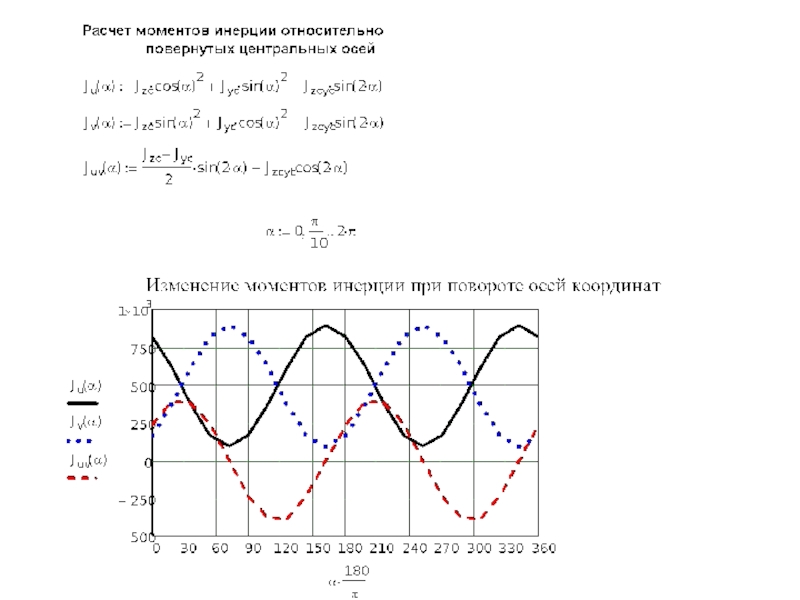
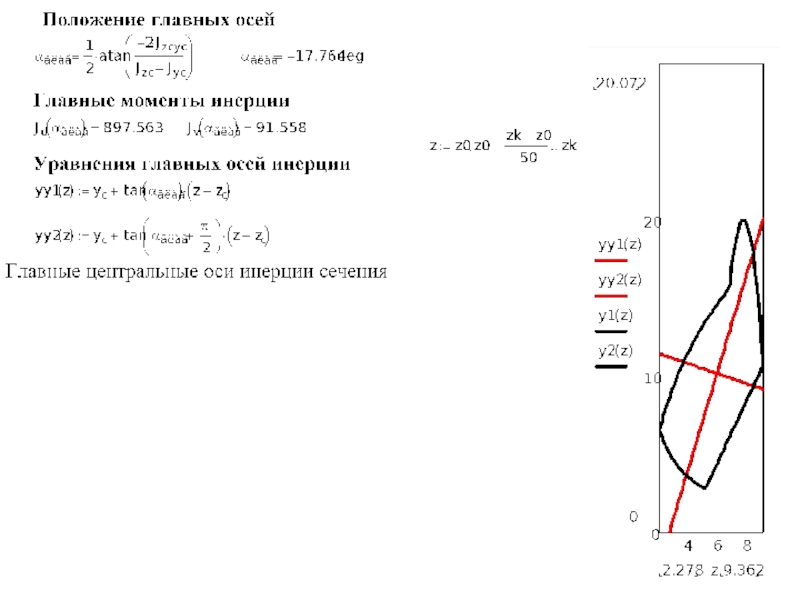
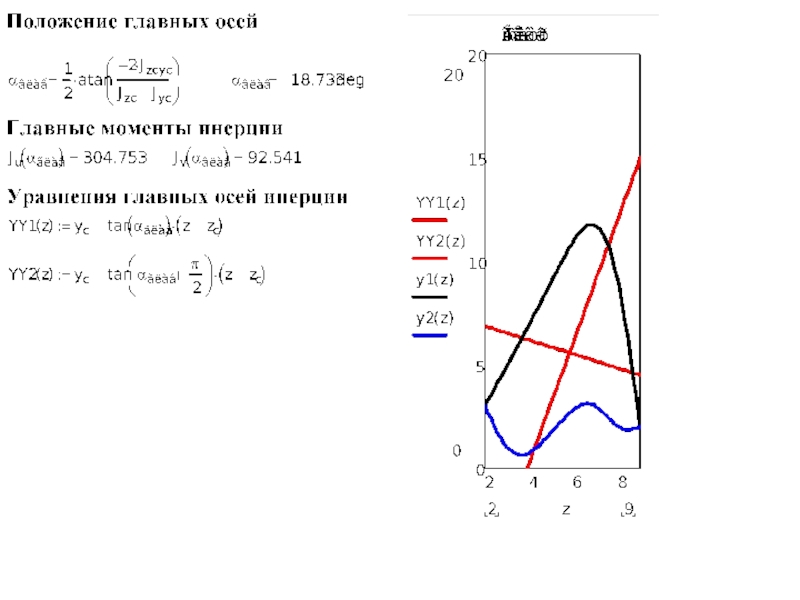
Слайд 105. Главные оси и главные моменты инерции сечения. Радиусы инерции.
Главными
Главные оси обозначаются цифрами 1 и 2
Моменты инерции относительно главных осей называются главными
Главные моменты инерции обозначают J1 и J2 , причем J1> J2.
Чтобы найти положения главных осей в данной точке О, выбирают в этой точке оси z и у для которых Jz,Jy, Jzy определяются проще всего.
Центробежный момент в главных осях (1;2) связан с центробежным моментом в осях (y;z) зависимостью
Слайд 11Так как по определению главных осей центробежный момент J12 должен быть
Нас интересуют первые два решения, т.е. n1=0, n2=1 получаем:
Из выражений для α1 и α2 заключаем, что главные оси взаимно перпендикулярны.
После определения α1 и α2 величины главных моментов инерции сечений J1 и J2 находятся по формуле
Находим значения α1, и α2, определяющие соответственно положения первой и второй главных осей, для чего решаем полученное уравнение
откуда
где n – любое целое число
Слайд 12Проведя преобразования можно получить, что
Для того чтобы понять смысл понятия главных
Откуда
Значения α из формул совпадают со значениями α для главных моментов. Следовательно, моменты инерции относительно главных осей достигают экстремальных значений, т. е. главный момент инерции J1, есть наибольший из всех моментов инерции относительно осей, проходящих через данную точку, а J2 - наименьший.
Слайд 13Радиусом инерции сечения относительно некоторой оси, например z, называется величина iz,
Радиусы инерции, соответствующие главным осям, называют главными радиусами инерции.
Слайд 146. Свойства моментов инерции геометрических фигур
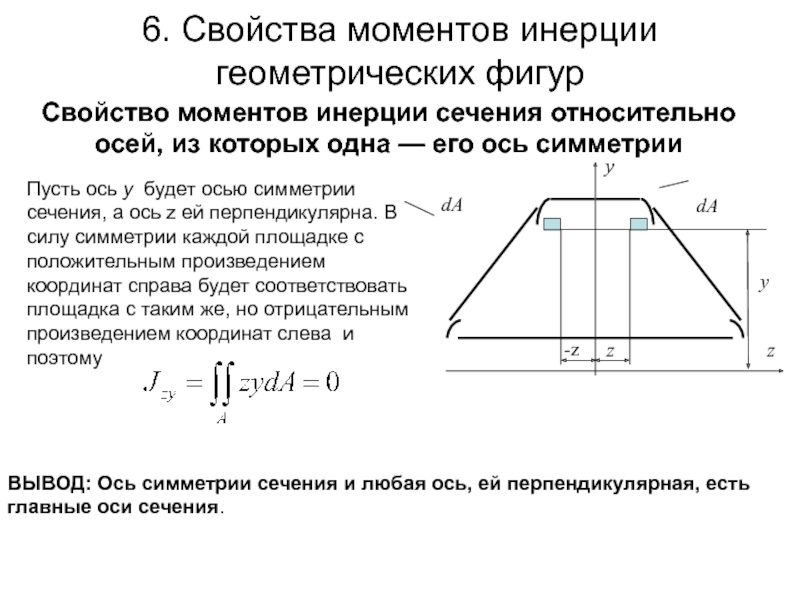
Свойство моментов инерции сечения относительно осей,
y
z
-z
z
y
dA
dA
Пусть ось у будет осью симметрии сечения, а ось z ей перпендикулярна. В силу симметрии каждой площадке с положительным произведением координат справа будет соответствовать площадка с таким же, но отрицательным произведением координат слева и поэтому
ВЫВОД: Ось симметрии сечения и любая ось, ей перпендикулярная, есть главные оси сечения.
Слайд 15Свойство моментов инерции правильных фигур относительно центральных осей
y
Для правильных фигур
Для
или
откуда
Для произвольной оси u, проходящей через центр
ВЫВОД: Моменты инерции правильных фигур относительно центральных осей равны и любые взаимно перпендикулярные центральные оси будут главными
или