- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гармонические колебания и их характеристики презентация
Содержание
- 1. Гармонические колебания и их характеристики
- 2. Колебаниями или
- 3. Периодом колебания
- 4. Частотой периодических
- 5. Циклической (круговой) частотой периодических колебаний называется число
- 6. Угол поворота определяет значение
- 7. В результате простейшее периодические колебаний совершается по гармоническому закону:
- 8. Скорость при гармоническом колебании – амплитуда скорости.
- 9. Ускорение при гармоническом колебании - амплитуда ускорения.
- 10. Графическое изображение гармонических колебаний посредством вращающегося вектора амплитуды называется методом векторных диаграмм.
- 11. Графическое изображение гармонических колебаний посредством вращающегося вектора амплитуды называется методом векторных диаграмм.
- 12. Ускорение и координата при гармонических колебаниях в
- 13. Уравнение гармонического колебания в комплексной форме имеет
- 14. 16. Квазиупругая сила. Период колебаний пружинного, математического и физического маятников.
- 15. Пружинный маятник. Колебания груза массой m на
- 16. Тело совершает гармонические колебания в случае действия
- 17. Математический маятник представляет
- 18. l – длина подвеса, g – ускорение свободного падения.
- 19. Физический маятник представляет собой твёрдое тело, совершающее
- 20. Колебания происходят под действием момента силы тяжести.
- 21. Для угла отклонения получаем дифференциальное уравнение гармонических колебаний
- 22. l* - приведенная длина физического маятника Период колебаний физического маятника
- 23. 17. Превращение и изменение энергии в системе
- 24. Превращение энергии рассмотрим на примере пружинного маятника.
- 25. Полная энергия колебательной системы определяется суммой энергий:
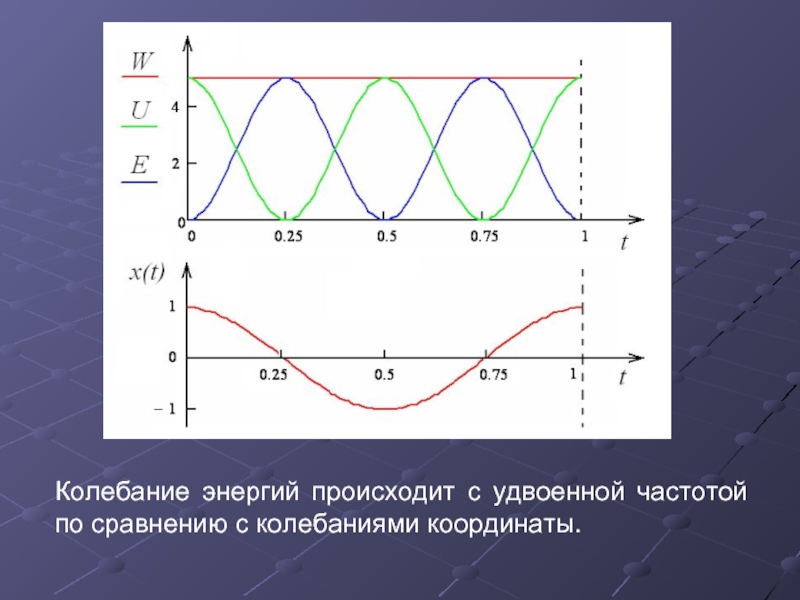
- 26. Колебание энергий происходит с удвоенной частотой по сравнению с колебаниями координаты.
- 27. Колебания кинетической и потенциальной энергии в колебательной системе происходит с удвоенной частотой 2ω.
- 28. Превращения энергии при колебаниях пружинного маятника происходят
- 29. В любой момент сумма кинетической и потенциальной энергии постоянна и равна полной энергии.
Колебаниями или колебательными движениями называются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени.
Слайд 2
Колебаниями или колебательными движениями называются движения или изменения состояния, обладающие той
или иной степенью повторяемости во времени.
Слайд 3
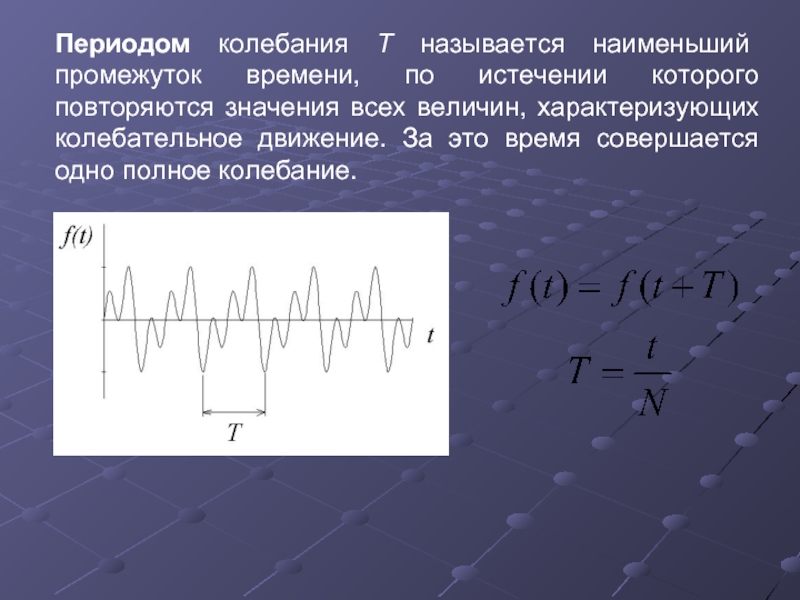
Периодом колебания Т называется наименьший промежуток времени, по истечении которого повторяются
значения всех величин, характеризующих колебательное движение. За это время совершается одно полное колебание.
Слайд 4
Частотой периодических колебаний ν называется число полных колебаний, которые совершаются
за единицу времени:
Слайд 5Циклической (круговой) частотой периодических колебаний называется число полных колебаний, которые совершаются
за 2π секунд:
Слайд 6
Угол поворота определяет значение х в данный момент времени и называется
фазой колебания.
Получить уравнение простейшего колебания можно, установив аналогию между вращательным и колебательным движением.
При вращении с постоянной скоростью проекция вектора на ось Х равна:
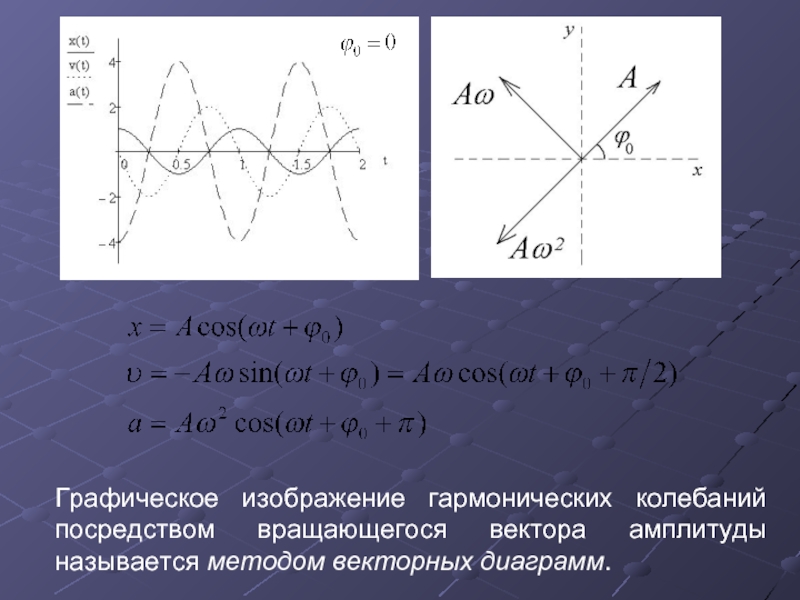
Слайд 10Графическое изображение гармонических колебаний посредством вращающегося вектора амплитуды называется методом векторных
диаграмм.
Слайд 11
Графическое изображение гармонических колебаний посредством вращающегося вектора амплитуды называется методом векторных
диаграмм.
Слайд 12Ускорение и координата при гармонических колебаниях в любой момент времени связаны
соотношением
или
представляющим собой дифференциальное уравнение гармонических колебаний. Решением уравнения является гармоническая функция.
Слайд 13Уравнение гармонического колебания в комплексной форме имеет вид
Физический смысл имеет лишь
действительная часть, обозначаемая
Согласно формуле Эйлера
Слайд 1416. Квазиупругая сила. Период колебаний пружинного, математического и физического маятников.
Слайд 15Пружинный маятник. Колебания груза массой m на пружине жесткостью k совершаются
под действием силы упругости пружины
Ускорение телу сообщает сила упругости
Слайд 16Тело совершает гармонические колебания в случае действия на него квазиупругой возвращающей
силы.
Для определения частоты необходимо установить квазиупругий характер возвращающей силы, определить k.
Слайд 17
Математический маятник представляет собой материальную точку, подвешенную на невесомой нерастяжимой нити
и совершающую движение в вертикальной плоскости под действием силы тяжести
Слайд 19Физический маятник представляет собой твёрдое тело, совершающее колебания в поле каких-либо
сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Слайд 24Превращение энергии рассмотрим на примере пружинного маятника. Пусть колебания происходят по
закону
При гармонических колебаниях пружинного маятника происходят превращения потенциальной энергии упругой деформации
в его кинетическую энергию и наоборот
Слайд 27Колебания кинетической и потенциальной энергии в колебательной системе происходит с удвоенной
частотой 2ω.
Слайд 28Превращения энергии при колебаниях пружинного маятника происходят в соответствии с законом
сохранения механической энергии. Максимальные значения энергий равны друг другу:
