- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Галилео Галилей (1564 - 1642) презентация
Содержание
- 1. Галилео Галилей (1564 - 1642)
- 2. Исаак Ньютон (1643–1727) Надгробие на могиле Ньютона
- 3. ЗАКОНЫ НЬЮТОНА 1 закон Ньютона: Всякое тело
- 5. 2 закон Ньютона: Ускорение, приобретаемое телом относительно
- 7. 3 закон Ньютона: Силы, с которыми действуют
- 8. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА Рассмотрим механическую систему, состоящую
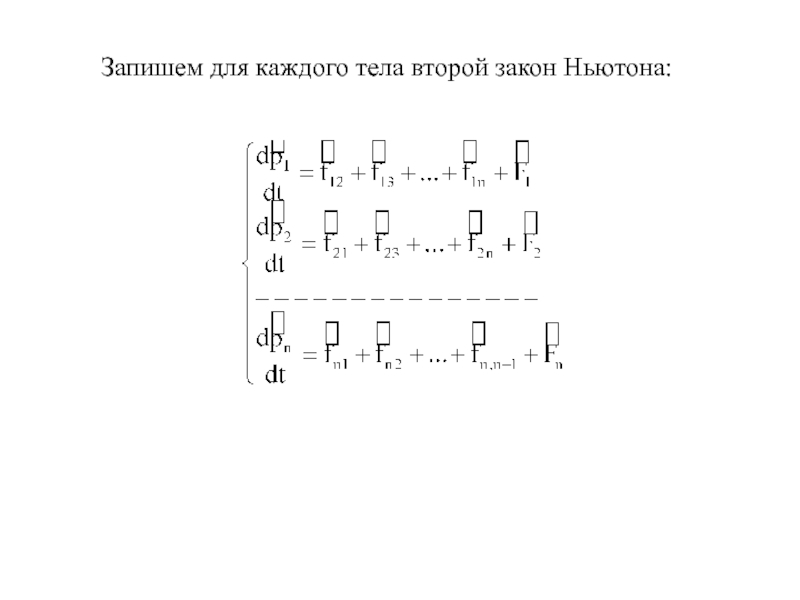
- 9. Запишем для каждого тела второй закон Ньютона:
- 11. Закон сохранения импульса: Полный импульс замкнутой
- 12. МОМЕНТ СИЛЫ Момент силы относительно точки [М]
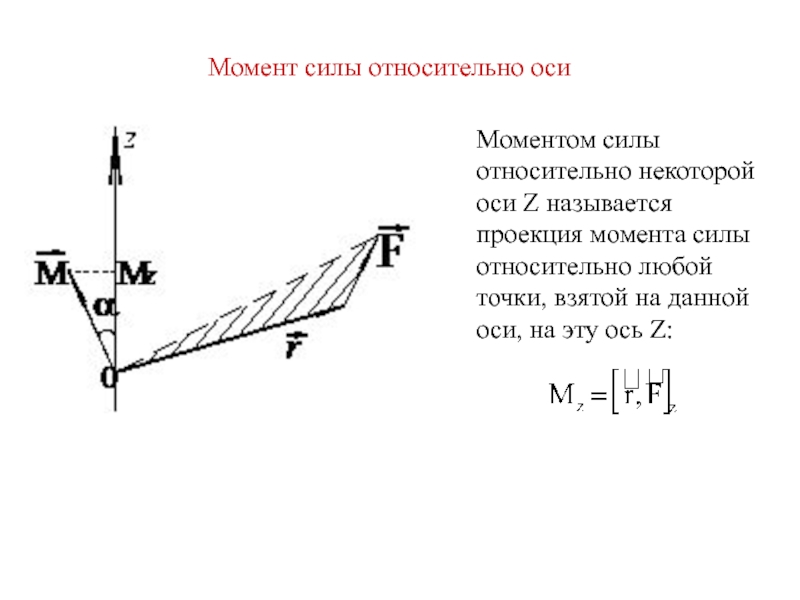
- 13. Момент силы относительно оси Моментом силы относительно
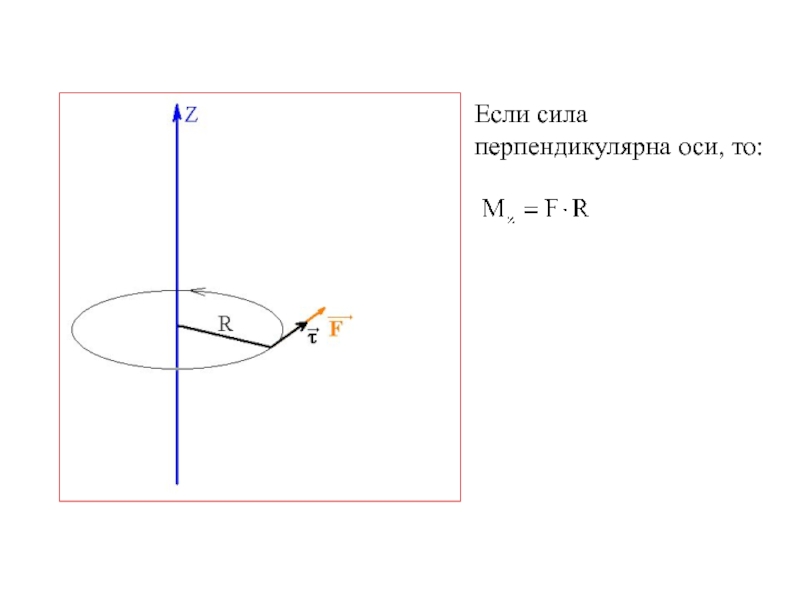
- 15. Если сила перпендикулярна оси, то:
Исаак Ньютон (1643–1727) Надгробие на могиле Ньютона
Слайд 3ЗАКОНЫ НЬЮТОНА
1 закон Ньютона: Всякое тело находится в состоянии покоя или
равномерного и прямолинейного движения, пока воздействие со стороны других тел не выведет его из этого состояния
Система отсчета, относительно которой выполняется первый закон Ньютона называется инерциальной.
Рассмотрим две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно, очевидно, будет двигаться с ускорением.
Слайд 52 закон Ньютона: Ускорение, приобретаемое телом относительно инерциальной системы отсчета, прямо
пропорционально действующей на него силе, обратно пропорционально массе тела и совпадает по направлению с силой
- равнодействующая всех сил, действующих на тело
Слайд 73 закон Ньютона: Силы, с которыми действуют друг на друга взаимодействующие
тела, равны по модулю и противоположны по направлению.
Слайд 8ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Рассмотрим механическую систему, состоящую из n тел.
Механическая
система называется замкнутой или изолированной, если на нее не действуют внешние силы (система не обменивается с внешними телами энергией).
Система называется незамкнутой, если на неё действуют нескомпенсированные внешние силы.
Слайд 11Закон сохранения импульса: Полный импульс замкнутой
системы тел остается постоянным.
В частном случае: если Fвнешн. (х) = 0, то рх = const.
Слайд 12МОМЕНТ СИЛЫ
Момент силы относительно точки
[М] = 1 Н⋅м
Моментом силы относительно некоторой
точки О называется векторное произведение радиус-вектора проведенного из точки О в точку приложения силы, на вектор силы F :
Слайд 13Момент силы относительно оси
Моментом силы относительно некоторой оси Z называется проекция
момента силы относительно любой точки, взятой на данной оси, на эту ось Z:
