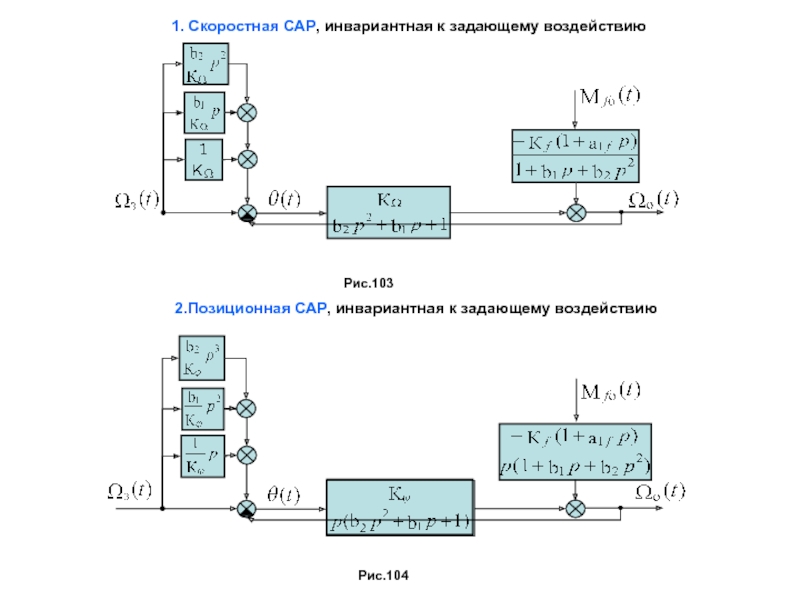
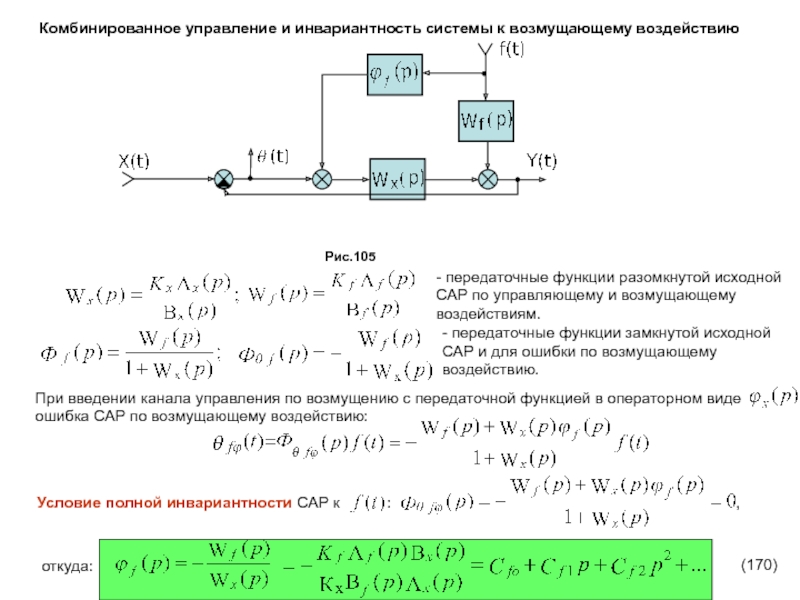
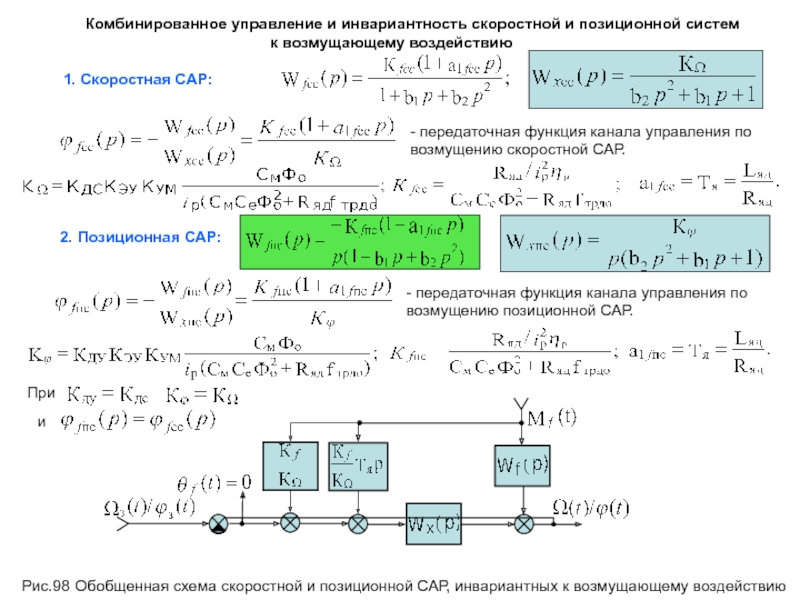
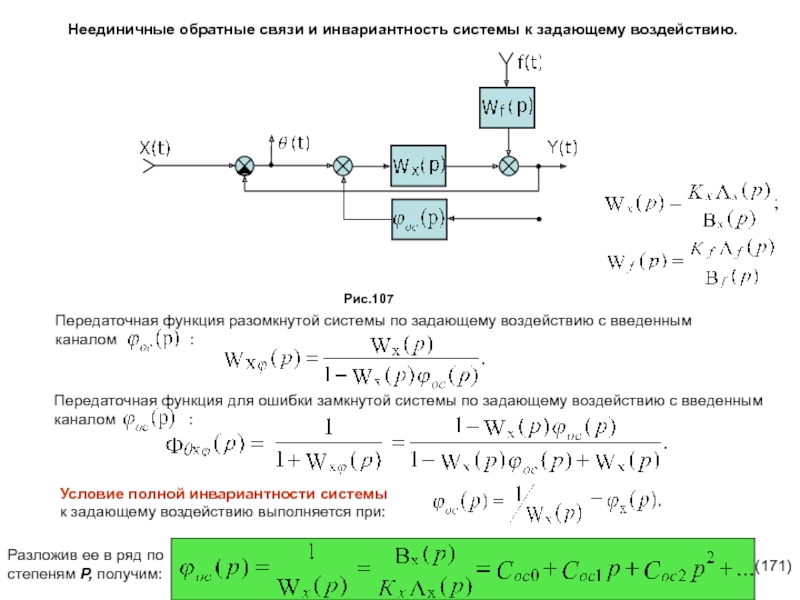
является отрицательность вещественных частей всех корней характеристического уравнения системы.
Отображая корни ХУ на комплексной плоскости, легко убедиться, что корни с отрицательной вещественной частью будут находиться слева от оси мнимых.
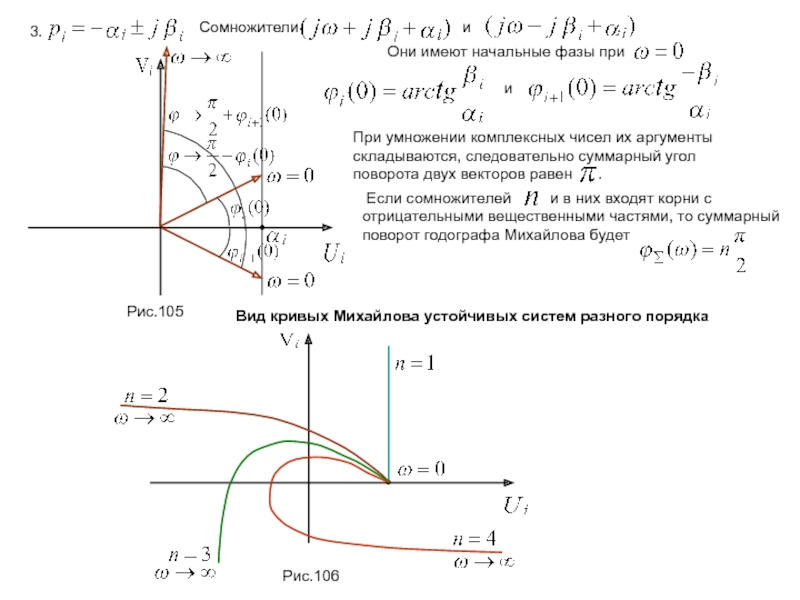
Рис.106
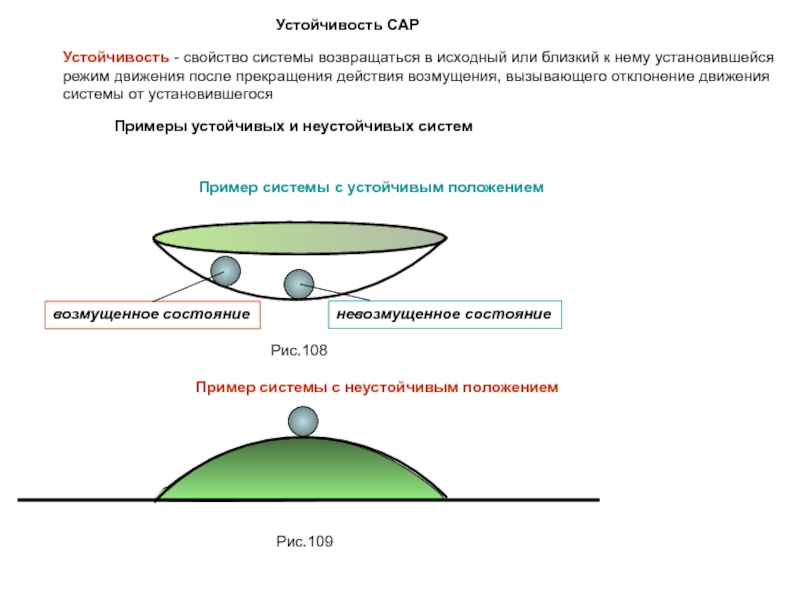
Корневой критерий устойчивости
можно сформулировать так:
Система устойчива, если все корни ее характеристического уравнения лежат на комплексной плоскости слева от оси мнимых, т.е. имеют отрицательные вещественные части.
Если хотя бы один вещественный корень или пара комплексных корней лежат в правой полуплоскости,
система неустойчива.
Границей устойчивости является ось мнимых
Система будет на границе устойчивости, например, при чисто мнимых корнях.
В этом случае в ней будут протекать незатухающие колебания, поэтому ось мнимых называют колебательной границей устойчивости.
Если вещественный корень равен 0, система тоже находится на границе устойчивости.
Она будет устойчива не относительно регулируемой переменной, а относительно скорости ее изменения. Такие системы называют нейтрально устойчивыми.