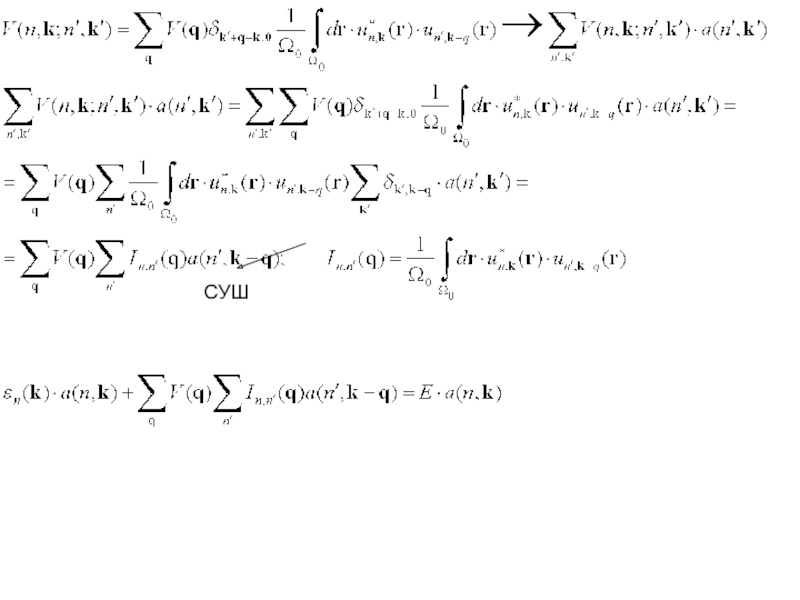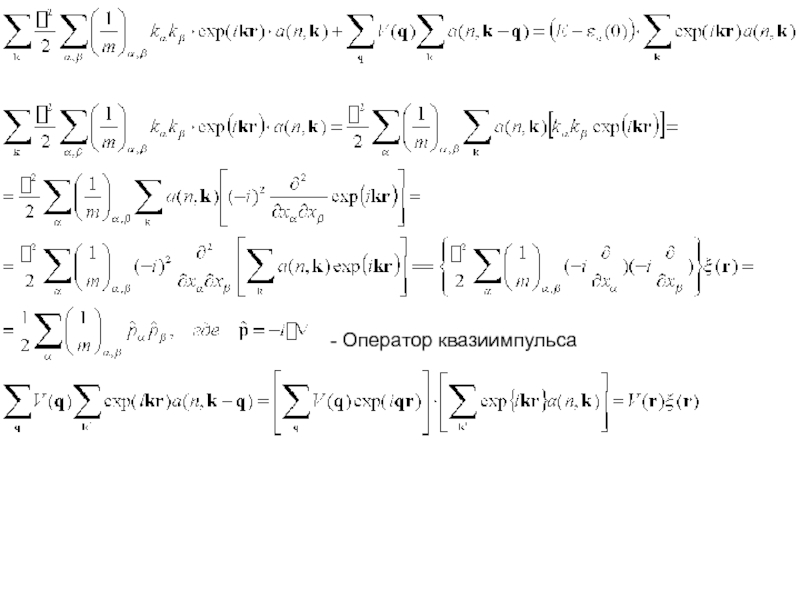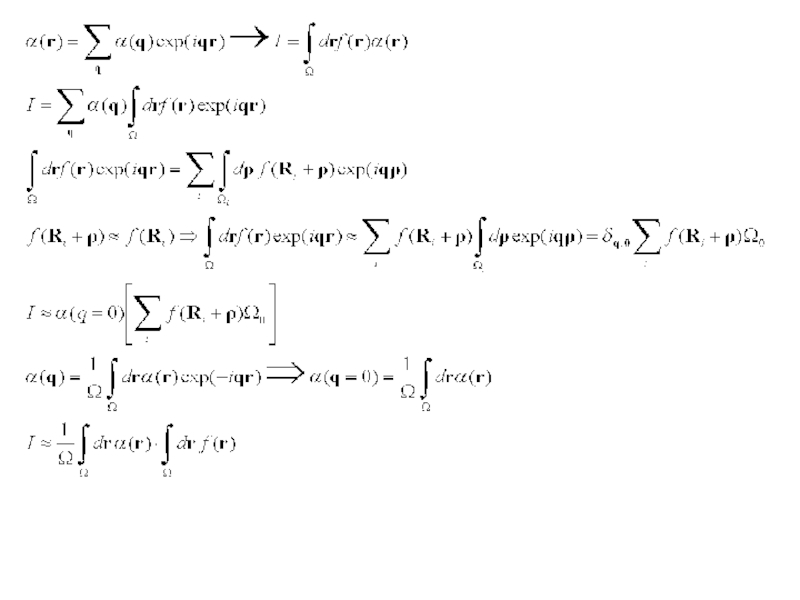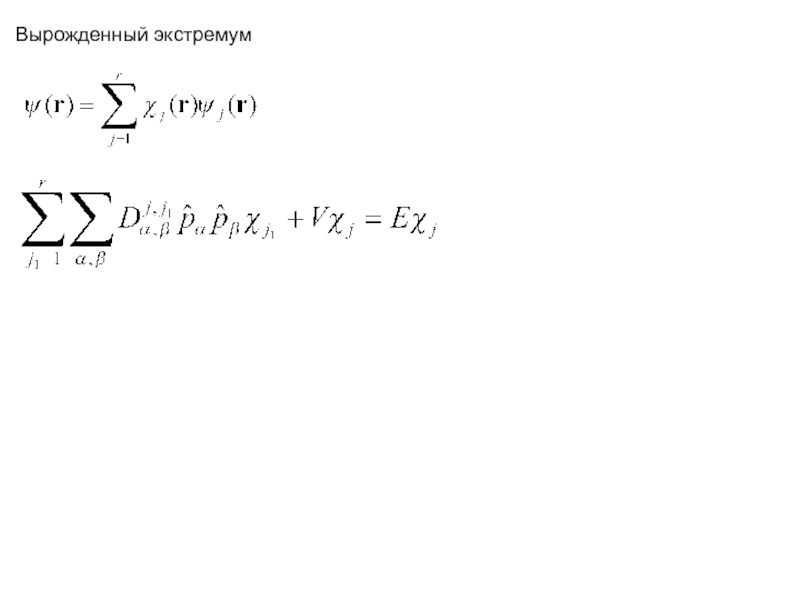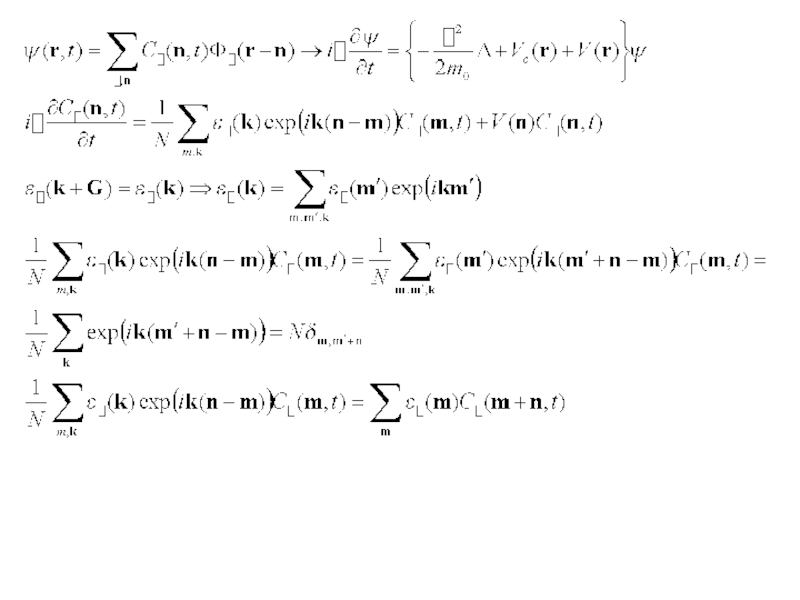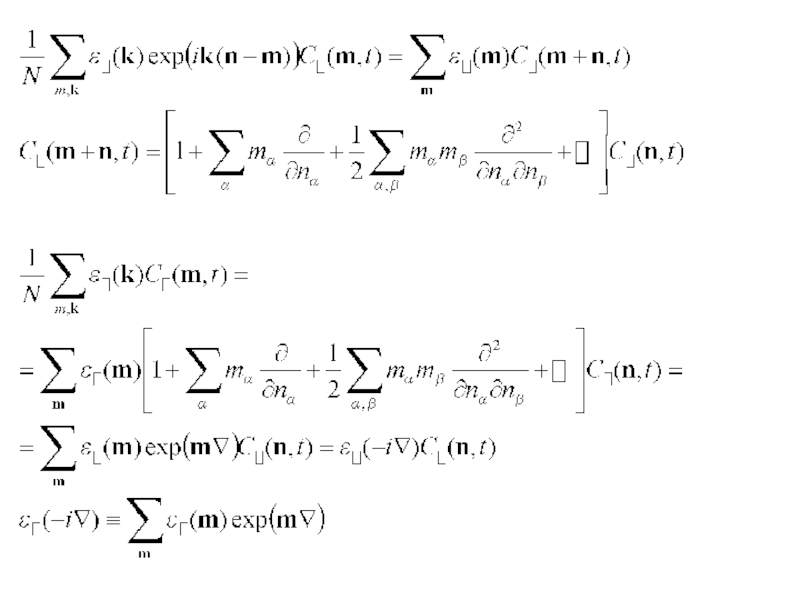- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формализм огибающей функции презентация
Содержание
- 1. Формализм огибающей функции
- 2. Метод эффективной массы На блоховский электрон наложен
- 3. Все ячейки – одинаковые +u –
- 4. решеточная сумма
- 5. СУШ
- 6. Потенциал V медленно меняется на межатомном масштабе
- 7. Пусть V=V0=const - состояния не изменяются
- 8. Волновая функция возмущенных состояний, возникших из состояний
- 9. - Оператор квазиимпульса
- 10. Волновая функция возмущенных состояний, возникших из состояний вблизи экстремума k0=0 - оператор квазиимпульса
- 11. Для описания термодинамических явлений нужно уметь вычислять
- 13. Зная только огибающую можно описывать макроскопические явления
- 14. Вместо реальных электронов в кристалле можно рассматривать квазичастицы с эффективными массами.
- 15. 1) вблизи дна невырожденной зоны с параболическим
- 16. Магнитное поле - вблизи дна - вблизи потолка
- 17. Вырожденный экстремум
- 18. Узельное представление. Функции Ваннье. Общий формализм огибающей
- 19. Внешний потенциал практически не меняется в пределах
- 20. 2) Функции Ваннье зависят от разности r-n
- 21. 4) Функции Ваннье являются ортонормированными 5)
- 24. На межатомном масштабе V меняется слабо =>
- 25. В случае медленного внешнего потенциала термодинамические
- 26. В случае медленного внешнего потенциала термодинамические свойства
- 27. Стационарные состояния блоховского электрона в однородном электрическом поле. Лестницы Ваннье-Штарка.
- 28. Примесные состояния в полупроводниках Донорные примеси –
- 29. - Атом водорода - непрерывный спектр
- 30. Акцепторные примеси – валентность меньше, чем у
Слайд 2Метод эффективной массы
На блоховский электрон наложен дополнительный потенциал V, внешний по
- потенциал медленно меняется, оставаясь практически постоянным в пределах элементарной ячейки
СУШ в блоховском представлении (в представлении по базису из волновых функций Блоха)
Слайд 3
Все ячейки – одинаковые +u – периодические функции с периодом решетки
r
r’
Ri
Замена переменной
0
i
Слайд 6Потенциал V медленно меняется на межатомном масштабе => основной вклад дают
Ограничимся нулевым членом
Слайд 7Пусть V=V0=const
- состояния не изменяются
V(r) меняется медленно =>Основной вклад в V(q)
- Огибающая (тот же порядок скорости изменения, что и у V)
Слайд 8Волновая функция возмущенных состояний, возникших из состояний вблизи экстремума k0=0
В случае
Умножаем обе части на exp(ikr) и суммируем по k
Слайд 10Волновая функция возмущенных состояний, возникших из состояний вблизи экстремума k0=0
- оператор
Слайд 11Для описания термодинамических явлений нужно уметь вычислять матричные элементы макроскопических величин,
- медленная функция , остающаяся практически постоянной в пределах элементарной ячейки
-быстропеременная функция, обладающей периодичностью кристаллической решетки
Слайд 13Зная только огибающую можно описывать макроскопические явления в кристалле.
Огибающую можно рассматривать
Слайд 14Вместо реальных электронов в кристалле можно рассматривать квазичастицы с эффективными массами.
Слайд 151) вблизи дна невырожденной зоны с параболическим невырожденным законом дисперсии имеем
2) вблизи потолка невырожденной зоны с параболическим невырожденным законом дисперсии имеем
Концепция дырки
Слайд 19Внешний потенциал практически не меняется в пределах элементарной ячейки.
Поэтому удобно использовать
- функции Ваннье
Функции Ваннье – линейные комбинации функций Блоха
Умножаем обе части разложения на exp(ikm) и суммируем по зоне Бриллюэна
Слайд 202) Функции Ваннье зависят от разности r-n
3) Набор функций Ваннье является
Функции Блоха образуют полную систему =>
Для набора функций Блоха выполнено условие полноты
Слайд 214) Функции Ваннье являются ортонормированными
5) Огромное преимущество функций Ваннье состоит в
- локализована в ячейке n и быстро убывает за ее пределами на расстояниях, порядка межатомных.
Пусть f(r) -медленно меняется на расстояниях, порядка межатомных
Слайд 24На межатомном масштабе V меняется слабо => в значения С в
- огибающая
Слайд 25
В случае медленного внешнего потенциала термодинамические свойства электронной подсистемы в кристалле
Слайд 26В случае медленного внешнего потенциала термодинамические свойства электронной подсистемы в кристалле
Слайд 27Стационарные состояния блоховского электрона в однородном электрическом поле. Лестницы Ваннье-Штарка.
Слайд 28Примесные состояния в полупроводниках
Донорные примеси – валентность больше, чем у основных
Мелкие примеси:
Расстояние от электрона до примеси>>постоянной решетки => можно рассматривать движение электрона в сплошной среде с диэлектрической проницаемостью ε
Размер иона << расстояния до электрона => поле иона можно разложить по мультиполям. Ион – заряженная система => оставляем только мультиполный член.
Слайд 29- Атом водорода
- непрерывный спектр => делокализованные состояния. Электрон свободно
- Связанные состояния
- в щели появляются дискретные уровни
Когда электрон находится на донорном уровне, он локализован на примеси. Переход в зону проводимости соответствует отрыву электрона.
Слайд 30Акцепторные примеси – валентность меньше, чем у основных атомов => возникает
- В щели возникают дискретные примесные уровни
Электрон, находящийся на примесном уровне, локализован на примеси. Переход из валентной зоны на акцепторный уровень – разрыв валентной связи, и захват на вакантную связь примеси